敲出型双障碍期权定价的高精度隐式差分格式

孙 玉 东

(贵州民族大学 商学院，贵阳 550025)

障碍期权在标准欧式期权的基础上增加了障碍触发限制条款,当障碍期权挂钩的风险资产触及障碍值之后期权即刻失效,此时期权的投资人也就损失了全部期权金.另一方面,期权作废也失去了套期保值、规避风险等功能,致使投资人直接暴露在市场风险之下.因此相较于其他期权障碍期权更加便宜,双障碍期权更是如此.

近些年来,学者和金融从业者们发现,价格相对低廉的障碍期权依然能通过一系列对冲策略实现套期保值、规避风险的功能[1-2],并且在投资策略的调整过程中投资人面临较小的期权金损失[3-4].此外障碍期权在其他金融工程领域也有着良好的应用[5-6].在理论价值分析方面,文献[7-8]采用傅里叶变换研究了双障碍期权的价值问题,给出了半解析定价结果的同时,进行了大量的实证分析.文献[4,9,10,11]采用摄动方法研究了障碍期权定价问题,给出了非线性 Black-Scholes模型上的一个半解析近似解,同时进行了近似结果的误差分析.由于障碍期权收益结构复杂,除了完全线性的 Black-Scholes模型外解析定价结果常常难以获取，文献[3,12]采用 Monte-Carlo模拟方法,获取了一种统计计量分析方法.

本文提出了采用加权隐式差分格式研究了双障碍期权定价问题.针对双障碍期权提出了一种更高精度的数值模拟方法,同时分析了差分格式的稳定性和收敛 性.

1 向上敲出巴黎期权

在期权存续期[0,T]内,双障碍期权约定当风险资产始终S位于区间[L,U]时则期权有效,否则期权作废.依据风险中性定价策略,双障碍期权的价值可以表示为

V=E[I{S(t)∈[L,U],t∈[0,T]}f(S(T))],

(1)

其中：

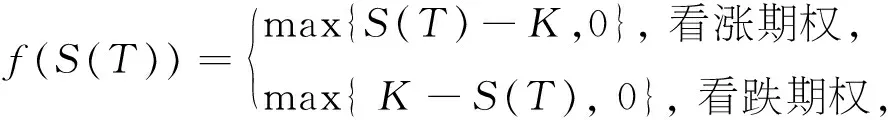
K表示事先约定好的执行价格.依据 Feymann-Kac公式,两种双障碍期权的价值适合下面的抛物初边值问题[1-2]

(2)

其中：r表示无风险利率,σ表示期权挂钩风险资产价格S的波动率,σ越大意味着风险资产S在未来时刻的走势不确定性约强.注意期权有规避风险、套期保值的功能,σ越大也意味着期权的功能越强,价值也越大.进一步将主方程结构简化,作变换x=lnS-lnL,则式(2)转化为[3]

(3)

其中：xmax=lnU-lnL.下文将对(0,T)×(0,xmax) 进行网格划分,采用隐式差分格式对双障碍期权进行价值分析.

2 差分格式

先对时间变量和空间变量进行等距网格划分,令

tk=kΔt,k=0,1,…,N;xi=ih,i=0,1,…,M,

其中： Δt=T/N和h=xmax/M分别表示时间步长和空间步长.进一步对时间变量进行离散,其中向前差分格式满足

(4a)

k=0,1,…,N-1.向后差分格式满足

(4b)

k=1,2,…,N.然后对空间变量进行网格划分,对任意的i=1,2,…,(M-1)有

O(h4),

(5)

O(h4),

(6)

其中：

考察加权隐式差分格式,将式(4a)、(5)、(6)代入式(3),由文献[13-14]可以得到

R(τk,xi)+O(Δt2+h4),

(7)

其中 ：

(8)

再利用式(3)的主方程,容易得到

(9)

对上式求偏微分并将上式代入,有

(10)

从而将式(9)、(10)代入式(8),则R(τk,xi)改写为

(11)

其中：

O(Δt2+h4).

(12)

(13)

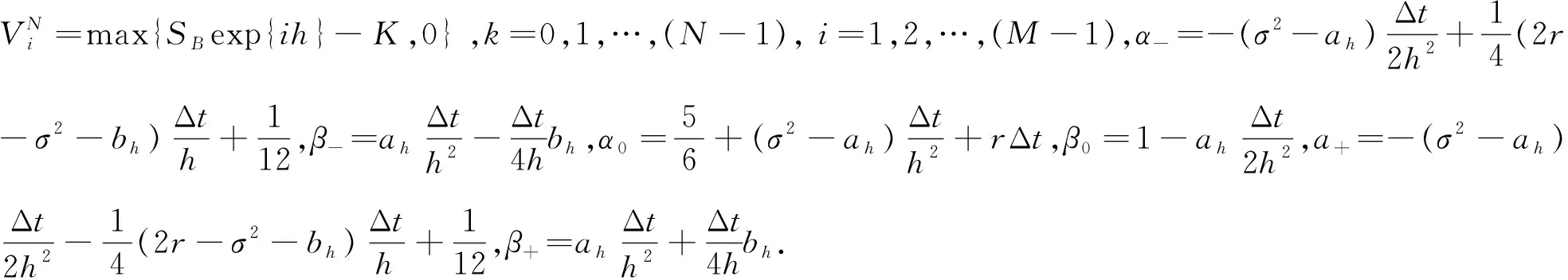
为了更好的进行编程实现,将隐式差分格式(13)还可以写成矩阵形式,

AVk=BVk+1,k=0,1,…,N-1,

(14)

3 稳定性和收敛性分析

本节分析隐式差分格式(13)的稳定性和收敛性.为了便于论述,这里先给出需要用到的无穷范数

(15)

这里可以断定差分格式 (13)的解是存在且唯一的.事实上,容易验证α0>0,并且当Δt较小时

α-+α0+α+=1+rΔt>0,

从而矩阵A是M-矩阵也是可逆矩阵.注意采用递推循环计算Vk时,BVk+1是常数向量,从而利用克莱默法则,线性方程组 (14)存在唯一解.

(16)

从而

(17)

其中：

定理 4.1 隐式差分格式(13)关于初值无条件稳定.

证明注意当k=N-1 时,注意α0>0 ,并且当h充分小时,α-<0,α+<0 ,从而由三角不等式,

注意到β-+β0+β+=1,有

(α-+α0+α+)‖εN-1‖∞≤‖εN‖∞,

又因为α-+α0+α+=1+rΔt,所以

‖εN-1‖∞≤(1+rΔt)-1‖εN‖∞≤‖εN‖∞.

因此由归纳法可得对任意的k=0,1,…,(N-1),有

‖εk‖∞≤‖εN‖∞

从而隐式差分格式 (13)关于初值无条件稳定.

容易得到

类推文献[13-14]中的傅里叶展开方法,差分格式 (13)存在如下收敛性结果.

定理 4.2 差分格式(13)一致收敛,并且对任意的k=0,1,2,…,N,

其中C是正常数.

4 数值模拟

本节用 R软件对隐式差分格式 (13)进行模拟,既验证差分格式有关精度的结果,又对双障碍期权进行价值分析.在模拟过程中,设定无风险利率r为 0.1,风险资产的波动率σ=0.3 ,风险资产在0时刻的市场价为100元,双障碍期权的到期日T=1 ,事先约定好的执行价格K=90 ,期权的下障碍L=50 ,上障碍U=200 .

先考察差分格式的精度,这里选择看涨类型的双障碍期权,其在到期日的收益满足

f(S)=max{S-K,0}

文献[15-16]给出了双障碍期权解析定价结果,结合式(15)、(16)可以计算差分格式在 0时刻的最大误差

依据文献[15-16],在固定时间节点总数N下差分格式在空间上的有效收敛精度为

同时在固定空间节点总数M下差分格式在时间变量上的有效收敛精度为

由表 1、 2,可以看出时间的收敛精度在 2附近、空间的收敛精度在 4附近,这恰好验证了定理 3的结果.由图1、2可以看出当(M,N)→ (∞,∞)时,差分格式 (13)不论在时间上还是空间上均一致收敛.

表1 N=100情形下的误差 EM|N和收敛速度 RM|N

表2 M=100情形下的误差EN|M 和收敛速度RN|M

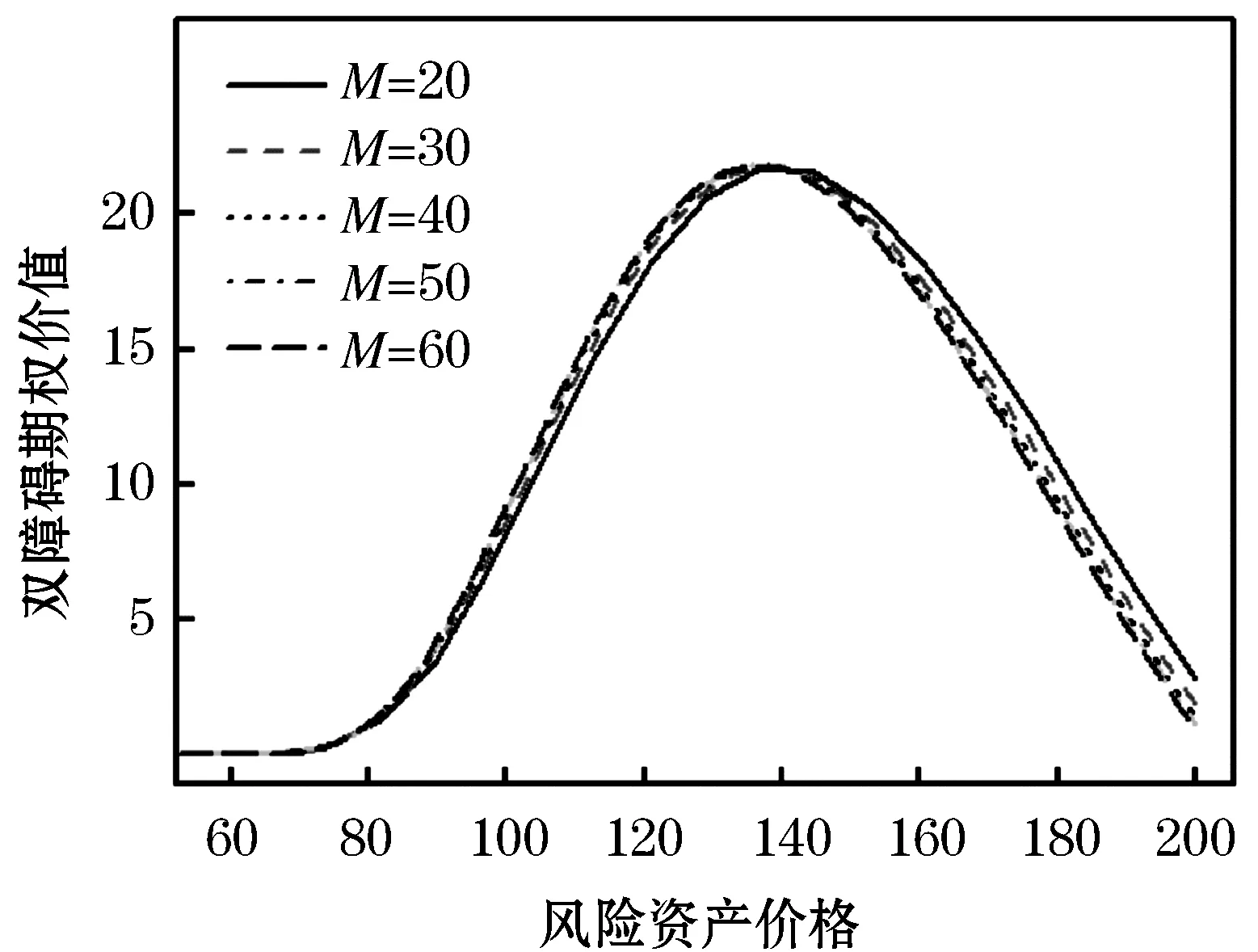
图1 不同股票价格S下双障碍期权价格

图2 不同时间t下双障碍期权价格 (S=100)

接下来分析双障碍期权的价值规律,由图 1可以看出当风险资产价格S接近上障碍U或者下障碍L时期权价值较低,处于中间区域时期权价值较高,这是因为当风险资产价格S接近上障碍U或者下障碍L时期权有较高的作废概率,期权的价值也就越低.由图 3、 4可以看出,当期权处于深度虚值状态时,期权价值随时间的推移走低,当期权处于深度实值状态时,期权价值随时间的推移走高.由图 5可以看出政府部门对无风险利率的管控对期权有实质性影响:期权处于实值状态时,无风险利率调高期权价值走低;期权处于虚值状态时,无风险利率调高期权价值走高.

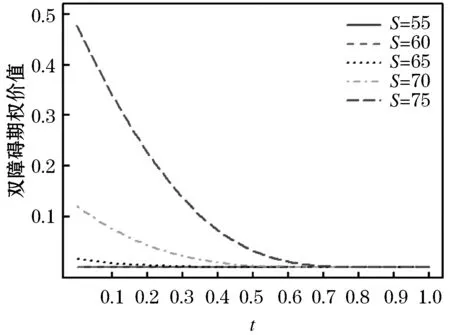
图3 不同时间t下双障碍期权价格 (虚值状态)

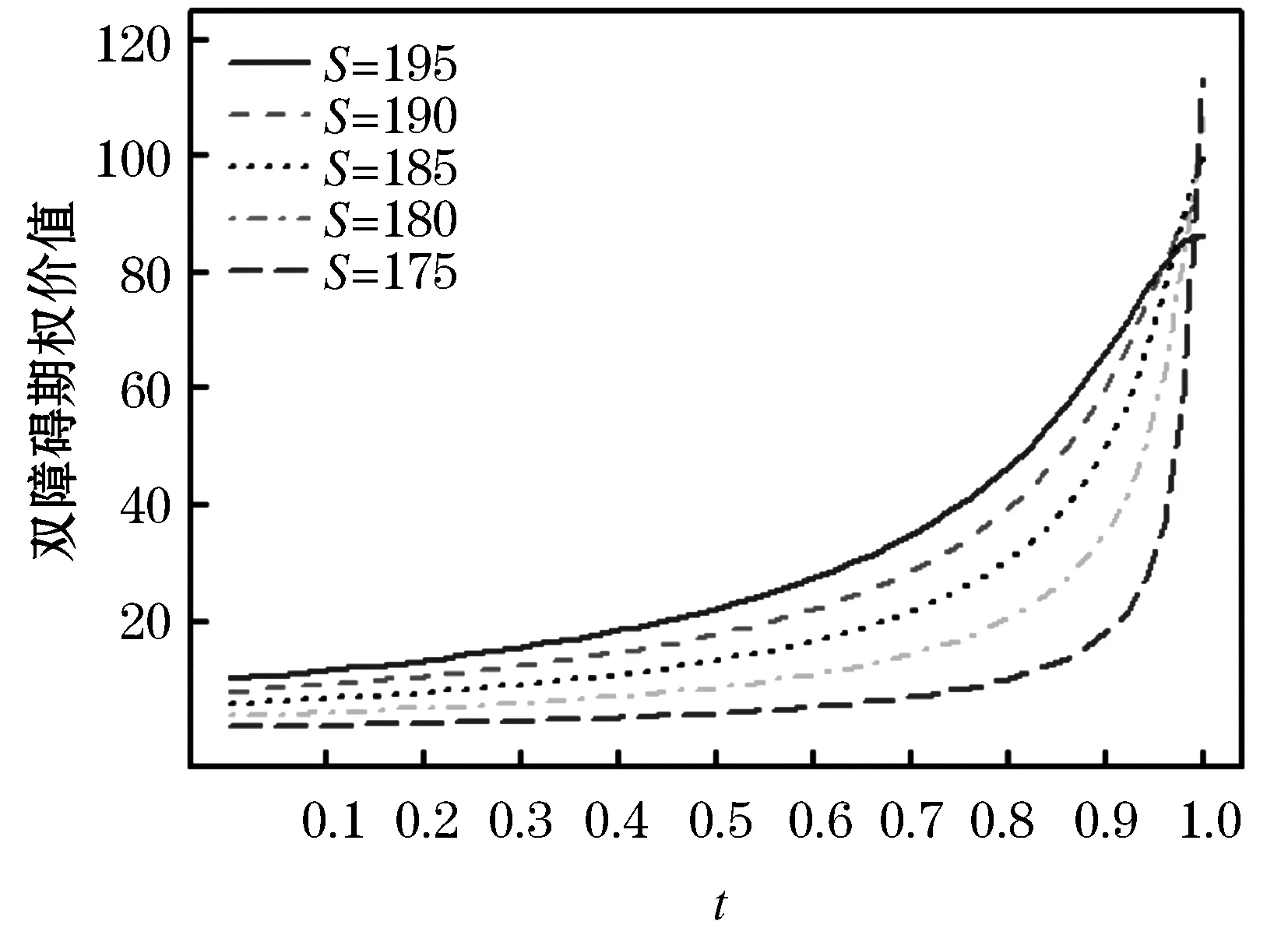
图4 不同时间 t下双障碍期权价格 (实值状态)

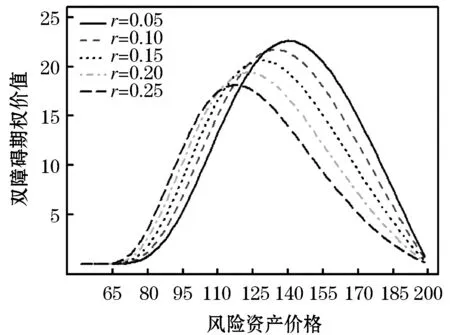
图5 不同风险资产价格下双障碍期权价格图

图6可以看出期权在金融市场上的规避风险功能,当风险资产处于障碍的中间区域时,波动率越大期权价值越大.当风险资产处于深度虚值或者深度实值状态时,由于期权存在较高的作废风险 ,使得波动率对期权价值的影响不易观测.

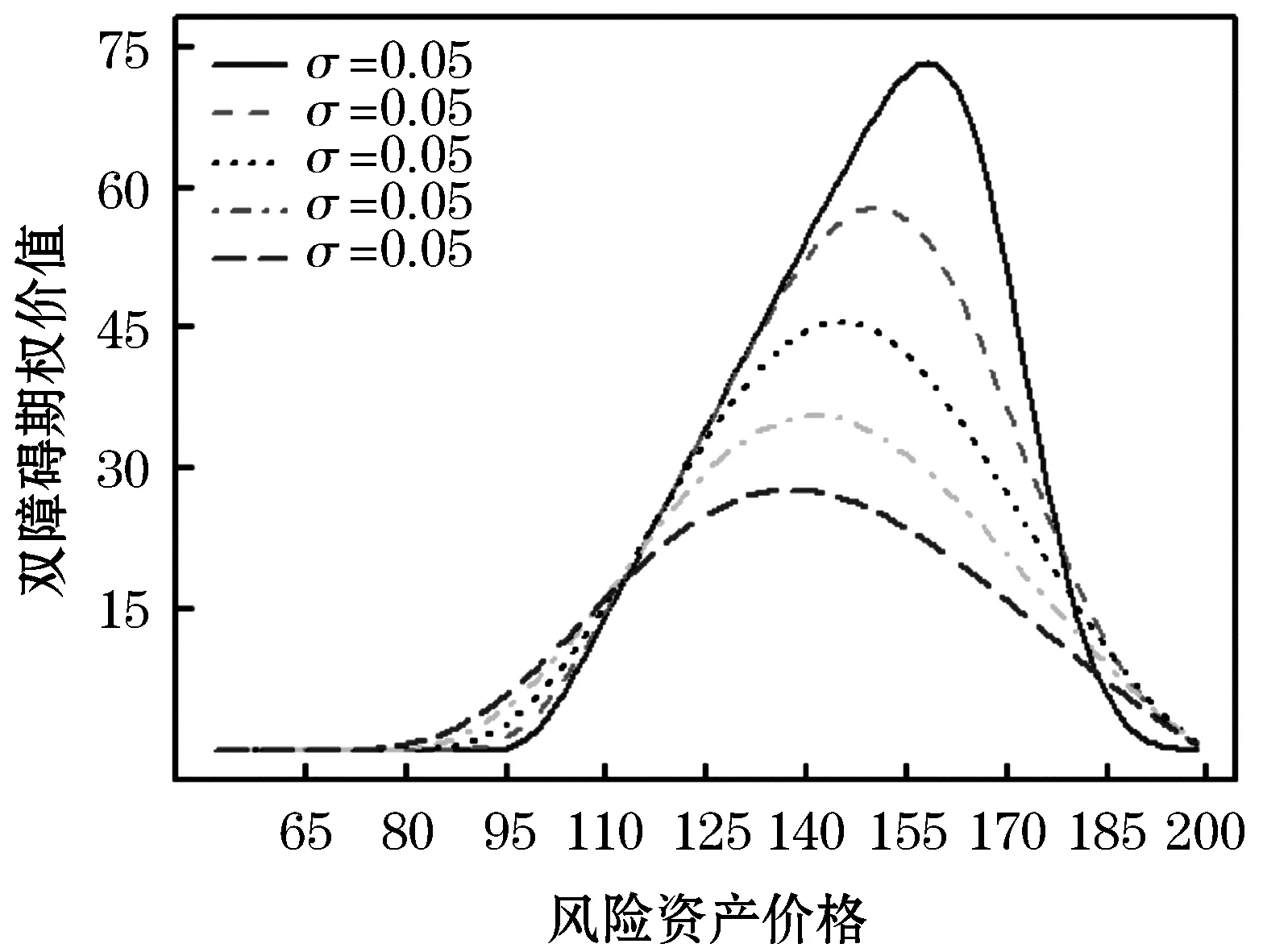
图6 不同风险资产价格下双障碍期权价格

5 结 语

随着金融经济的发展,期权逐步引起投资人的青睐.本文利用隐式差分格式考察了连续敲出型双障碍期权定价问题,得到一个精度相对高的差分格式,分析了差分格式的稳定性和收敛性等问题.在相同的计量模型下,本文提供的方法对其他欧式类型期权依然有效,但是针对近些年来研究的美式类型期权的差分定价结果以及相应的最佳实施边界仍需要进一步的研究.