基于多目标进化的聚类实现
2020-10-28汪宏海
汪 宏 海
(浙江旅游职业学院,杭州 311231)
聚类分析本质上可以看作是一个优化问题,采用不同的优化指标,聚类问题就不同.已有的聚类算法存在的主要问题是:只分析一种指标,因而无法适用于不同特征类型的数据.多目标优化算法能实现对多个不同目标的同时优化,受此启发,可以将聚类问题转化为对多个聚类指标的优化问题,从而获得更好的聚类性能[1].
进化算法适合求解复杂、非线性的问题,多目标进化是采用进化计算的方法对多目标优化问题进行求解.由于多目标优化问题通常是复杂、非线性的,因此,多目标进化算法非常适合求解这类问题.
基于多目标进化的聚类优化是目前的一个研究热点,涌现出很多代表性工作.文献[1]在多目标萤火虫算法中引入一种动态调整的变异机制以获得更加均匀分布的非劣解,其中以动态减小的概率选择个体,并采用类似于差分进化算法中变异算子的策略对其进行变异,通过自适应调整收缩因子以提高变异效率.文献[2]提出一种基于局部集成和克隆选择的多目标聚类算法.在聚类过程中,周期性的将聚类解集划分为若干邻域,对每个邻域进行局部集成操作,剔除各个类数下的不合理划分;利用克隆选择算法的思想构建3种变异算子,推动种群的进化,分别具有增大或减小当前解的聚类类数、调整当前解样本划分情况的功能.文献[3]提出一种基于密度估计的多目标免疫克隆聚类方法.该算法根据密度聚类的思想,通过引入核密度估计,解决了克隆算法中克隆规模的问题.文献[4]提出了一种基于分解的进化多标进化聚类算法,无需提前设定权重,提高了聚类效果.文献[5]提出了一种改进的离散多目标量子微粒群聚类算法,提出适合整数编码的离散量子微粒更新公式,对算法的性能提升起到了很大作用.
以上算法都是基于多目标的框架对某种单一聚类算法进行优化,由于各种聚类算法各具特色,如k-means(K均值)聚类算法适用于各类别样本量比较均衡的场合,若各类别样本分布不均,则不适用,此时,FCM(模糊C均值)可获得较好效果.因此,结合FCM和k-means的优点,本文提出一种改进的多目标进化聚类算法,该算法以多目标进化为框架,将FCM以及k-means聚类算法进行融合,以初始聚类中心作为迭代自变量,在计算个体适应度部分加入对FCM、k-means聚类结果的重排序操作和排序结果融合操作,保证聚类结果的多样性以及各类别之间的均匀性,并利用当代最优个体以及历史最优个体二次交叉,降低算法运行时间.实验结果表明了算法的有效性.
1 多目标聚类算法
聚类的效果一般使用如下两个指标:类内距离(Mean Index Adequacy:MIA)、类间距离(Mean of Distance between Curves:MDC).
类内距离MIA表示每个聚类中心和它对应的聚类中的所有样本特征的距离平均值,MIA数值越小说明类内样本的紧密度越强,聚类效果越好;反之,类内样本的紧密度越低,聚类效果越差,公式如下:
(1)
(2)
其中:c为聚类数目,Ck表示第c类样本中包含的特征集合个数;ntk表示该集合中的所有特征个数;nk表示第k类样本集中包含的单位数目;CTk表示第k类样本集的聚类中心,其中k=1,2,3,…,c.
类间距离MDC表示不同类的聚类中心样本集之间距离的平均值,MDC数值越大说明类间样本稀疏性越强,聚类效果越好;反之,类间样本稀疏性越低,聚类效果越差,计算如下:
MDC(c)=mean(d(CTk1,CTk2))
(3)
其中:k1和k2分别代表不同的类别,CTk1代表第k1类样本集的聚类中心,CTk2代表第k2类样本集的聚类中心,d(Ck1,Ck2)表示第k1类与第k2类样本集聚类中心的欧氏距离.
目标函数则可定义为下式:

(4)
对于一个好的聚类效果,必然满足MIA(类内离散度)足够小且MDC(类间离散度)足够大的原则,因此,聚类是一个多目标优化问题.
2 算法实现
算法的总体流程图如图1所示.
本文算法分为四个部分,分别为数据预处理、确定聚类数目、多目标进化聚类、聚类结果可视化.
2.1 数据预处理
1)特征重构
在特征重构部分应用谱聚类的特征处理方法,谱聚类是一种基于图论的聚类方法,通过对样本数据的拉普拉斯矩阵特征向量进行聚类,达到对样本数据聚类的目的.谱聚类可以理解为将高维空间的数据映射到低维,然后在低维空间用其他聚类算法(如k-means)进行聚类.
算法主要包括相似度矩阵W的计算、度矩阵D的计算、拉普拉斯矩阵L的计算和特征向量的计算[6].
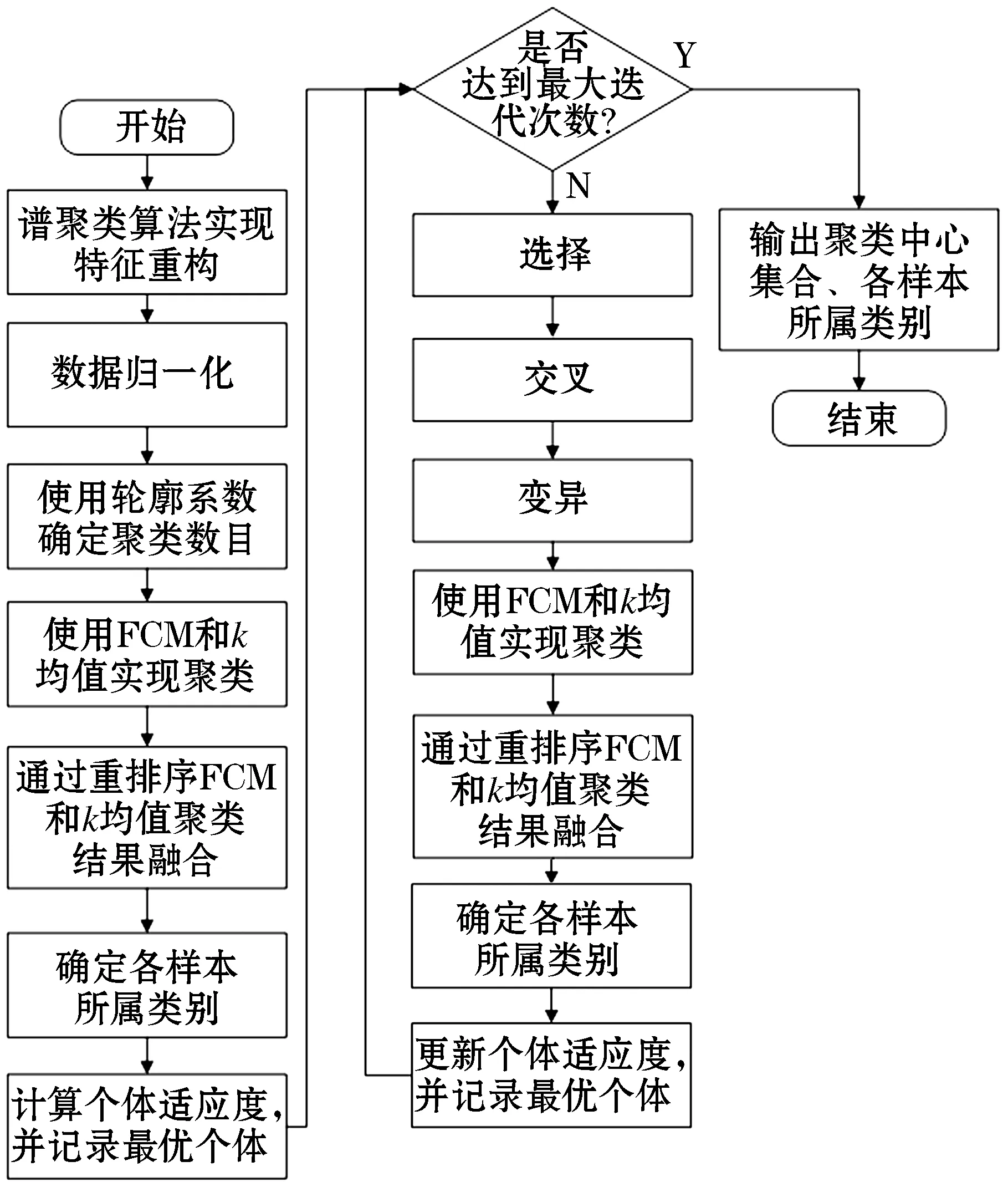
图1 算法流程图
2)数据归一化
在多维度的特征空间中,当各指标间的水平相差很大时,需要对原始指标数据进行标准化处理.这是因为:直接用原始指标值,将会突出某维度的特征的作用,相对削弱其他低维度特征的作用[7-8].
对特征矩阵进行归一化处理,计算公式如下:
(5)
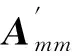
2.2 确定聚类数目
由于传统的FCM和k-means算法都需要通过预设聚类数目即聚类中心的个数,才能进行聚类中心的迭代,所以,在数据进行预处理之后,需要确定聚类数目.本文引入轮廓系数(SC)作为聚类数目确定的评价指标.
轮廓系数是一种结合类内凝聚度和类间分离度的内部评价指标,对于样本点i来说,其轮廓系数的数值计算如下[9]:
(6)
其中:a(i)是样本点i与类内所有样本的欧几里得距离的平均值;b(i)是样本点i与最近其他类内样本点欧几里得距离的最小值,该最小值取值范围为[-1,1].
因此,对于整个样本集合来说,总体轮廓系数(SC)的计算公式为[10-11]:
(7)
其中:n为样本点总数,SC数值越大,则类内凝聚度越高,类间分离度越高,反之两个指标均越低.
通过预设聚类数目的范围为[Cmin,Cmax],分别采用FCM和k-means算法对[Cmin,Cmax]进行聚类求取轮廓系数的数值;进而确定最优的聚类数目Cbest,计算公式如下[12]:
(8)
其中:Cmax,FCM、Cmax,k-means分别为FCM和k-means算法在[Cmin,Cmax]内求得轮廓系数最大数值时的聚类数目,round是四舍五入取整符号.
2.3 多目标聚类
多目标聚类包括初始种群的产生、选择、交叉、变异和个体适应度计算.
1)编码
编码采用实数编码方式,其中每一个体都包含m×m个十进制染色体,也即每m个染色体代表一个聚类中心归一化后的数值,可以是1-m之间的随机整数.
2)初始种群的产生

X=
(9)
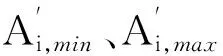
3)选择
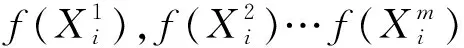
4)交叉
交叉具体过程为:利用当代的最优个体以及历史最优个体分别与当代其他个体进行二次交叉,形成下一代的新个体.该部分与传统交叉不同的是能降低算法搜索次数,快速找到全局最优解.
5)变异
对某一节点所属分类以概率pm随机改变,也即:对于第i个种群的第j个个体的第k个染色体是否进行变异,公式如下:
(10)
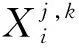
6)聚类结果重编码
由于传统聚类算法对聚类结果分类标签都是随机定值的,如对6个节点网络进行分类的结果可能有[1,1,2,2,3,3]或者[2,2,3,3,1,1],其实是相同的分类效果,即节点1、2为一类,节点3、4为一类、节点5、6为一类,因此需要提出一种聚类结果重编码,对聚类结果进行规范化,从节点1开始将其分类标签修正为1,并将其原来为同一分类标签的节点变为1;进而随着节点号的增长将分类标签进行步长为1的修正.如对于一个6节点网络,原分类标签为[2,2,3,3,1,1];则修正后标签为[1,1,2,2,3,3].
7)对当代种群进行解码
首先,将个体的聚类中心分别输入FCM和k-means聚类算法进行迭代,求得分类结果并进行重编码.假设两个聚类算法求得分类分别为RCFCM,RCk-means二者皆为1×D的矩阵,D为节点的数目,对于节点d的类别号,通过聚类结果的融合可以得到融合后的节点分类类别为:
(11)

然后,用各分类的类内样本计算聚类中心.进而,计算当代各个体所对应的两个目标函数,MIA以及MDC数值;对Pareto解进行优秀个体的选取.
3 实验分析
本文实验机器CPU为i5-4200H@2.80GHz,内存为12GB,分别用UCI数据集和人工数据集对算法的聚类有效性进行检验.
3.1 评价指标
本文选取两个外部指标对聚类效果进行评价,分别是Adjusted Rand Index (Rand) 和Jaccard[13-14].
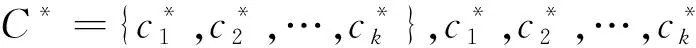
Rand和Jaccard计算公式如下:
(12)
(13)
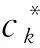
3.2 UCI数据集
3.2.1 聚类数目确定
选取WINE、X8D5K、HEART、IRIS和VOTE数据集作为待聚类的数据集[15],待确定聚类数目范围为[2,14],对每个聚类数目进行20次实验得到轮廓系数均值,取轮廓系数最大时所对应的聚类数目作为待聚类数目.通过实验,得到的实验结果如表1所示.
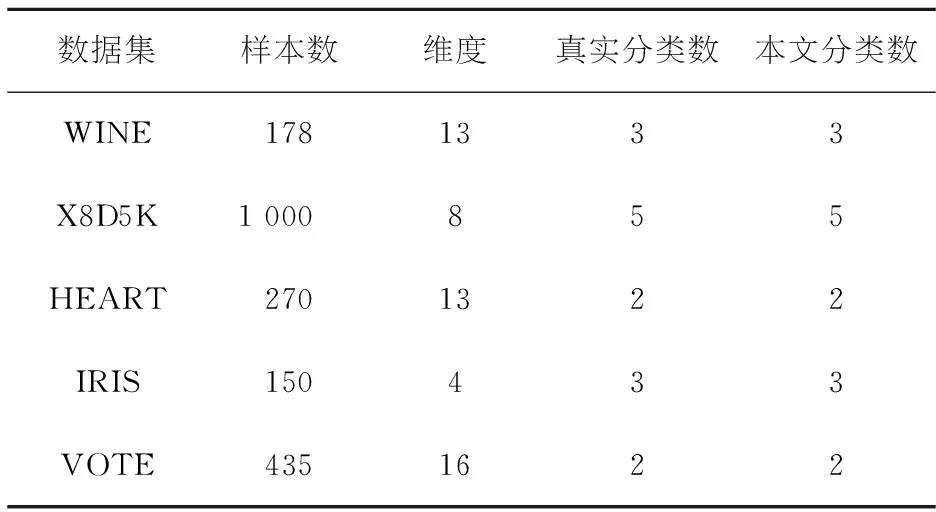
表1 UCI数据集属性
从表1可知,本文算法得到的最优聚类数目与实际分类数目一致.
3.2.2 聚类有效性校验
对于改进的多目标进化算法,设置寻优的自变量的上下限分别为0、1,算法的种群规模为100、迭代次数为200,对最后一代的Rand和Jaccard进行求均值,作为该数据的聚类的外部评价指标.
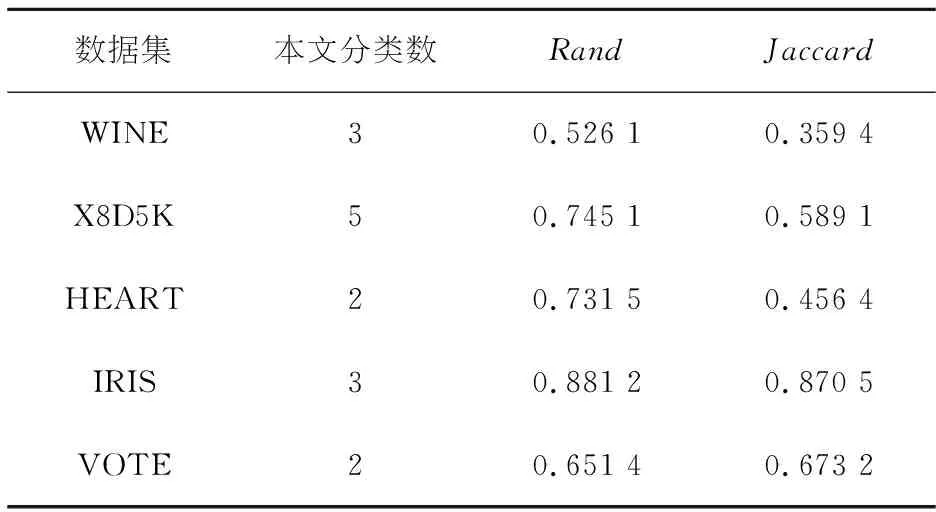
表2 UCI数据集聚类有效性
从表2可知,总体来说,本文算法能有效实现UCI数据集的聚类.
3.3 人工数据集
3.3.1 聚类数目确定
选取TWOMOONS、TWO CLUSTER、THREECIRCLES、THREE CLUSTER、SPIRAL和SPIRAL_UNBALANCE数据集作为待聚类的数据集,待确定聚类数目范围为[2,14],对每个聚类数目进行20次实验得到轮廓系数均值,取轮廓系数最大时所对应的聚类数目作为待聚类数目.通过实验,得到实验结果如表3所示.
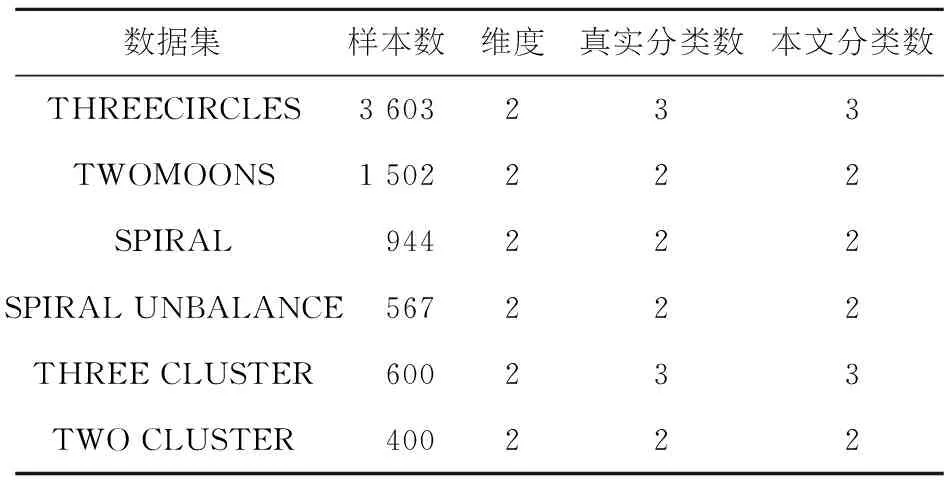
表3 人工数据集属性
从表3可知,本文算法得到的最优聚类数目与实际分类数目一致.
3.3.2 聚类有效性校验
对于改进的多目标进化算法,设置寻优的自变量上下限分别为0、1,算法种群规模为800、迭代次数为200,对最后一代的Rand和Jaccard进行求均值,作为该数据的聚类的外部评价指标.
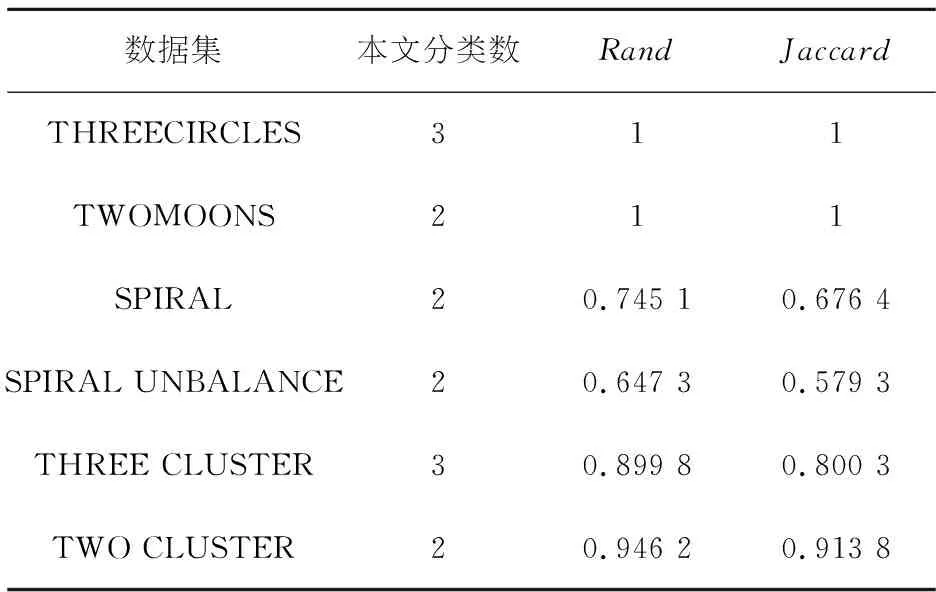
表4 人工数据集聚类有效性
从表4可知,总体来说,本文算法能有效实现人工数据集的聚类,但对于流行图形的聚类效果还不够理想.
4 结 语
本文提出一种多目标进化的聚类算法,该算法以多目标进化为框架,将FCM、k-means聚类算法进行融合,设计了改进的进化算法.实验结果表明了算法的有效性.
