简支现浇箱端横梁的受力模型研究
2020-10-28郑庆平
郑 庆 平
(福建省交通规划设计院有限公司, 福建 福州 350004)
现浇箱梁因其具有整体性好、抗扭刚度大、能适应各种线型及桥宽、断面可塑性强等优点,而被广泛应用于现有桥梁建设中。其中,端横梁和中横梁是箱梁横向联系的主要受力构件,通过连接各个腹板来提高箱梁的横向刚度[1-3]。虽然,现浇箱梁在我国已大量建设,技术也日趋成熟,但是端横梁的受力依然复杂,精确化分析难度较高,为此,仍有必要对其进行受力性能研究。
目前,部分学者对端横梁的受力模型进行了相关研究。陈维晃等[4]采用ANSYS软件研究横梁受力状况对桥梁的稳定性和耐久性的影响。刘泰松等[5]、柳双军[6]运用MIDAS软件研究箱梁横梁的受力,并提出横梁计算时纵向恒载的分配比例及方式。林峰等[7]通过建立实体有限元模型探讨了常规箱梁横梁的计算模式,并提出一套新的计算方法。朱文卫[8]对槽形梁端横梁的设计计算进行了相关研究。
虽然,目前关于箱梁端横梁设计计算的研究较多,但是尚未有统一的理论。为此,本文以某工程实例为背景,运用桥博有限元软件建立箱梁端横梁模型,研究不同恒载分配比例以及传力方式对端横梁受力性能的影响,并得到最不利状况下的设计条件,其研究结果可为简支现浇箱端横梁的设计计算提供参考与借鉴。
1 端横梁理论模型
1.1 模型截面
由规范[9]可知,当箱梁端横梁为预应力混凝土结构时,其模型截面设为工字型,如图1(a)所示;当箱梁端横梁为钢筋混凝土结构时,其模型截面设为矩形,如图1(b)所示。
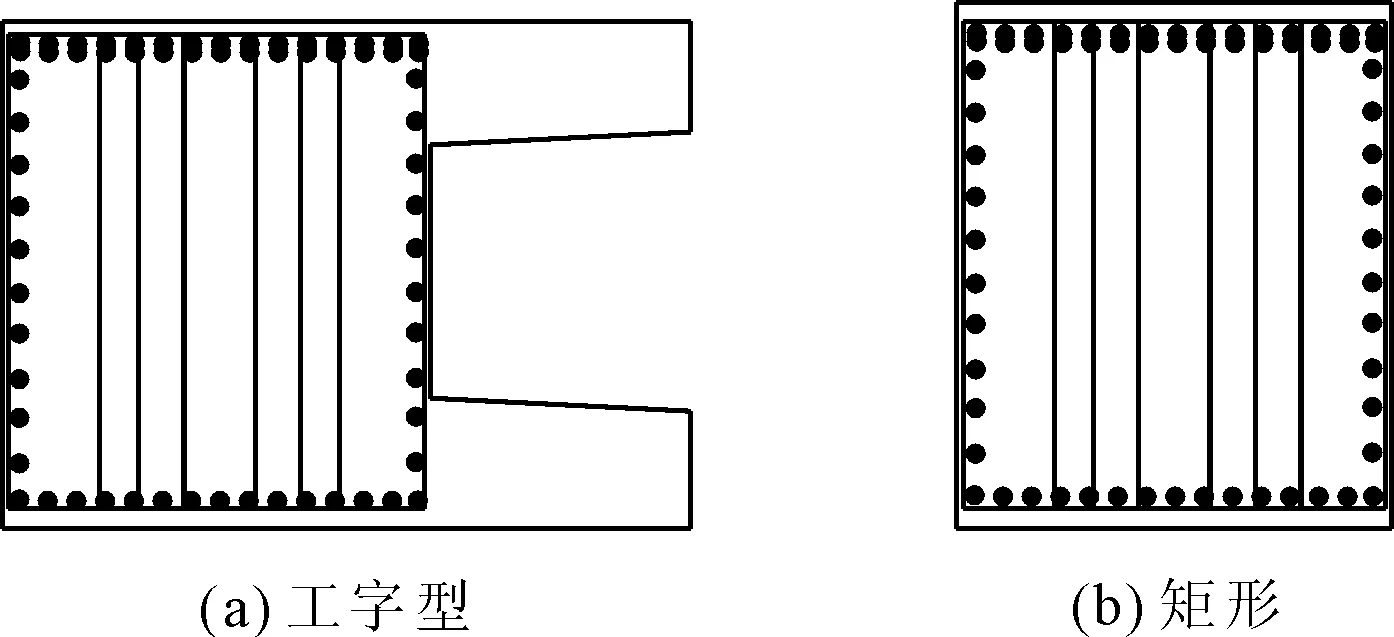
图1 端横梁计算截面
1.2 恒载分配方式
本文仅研究等间距腹板箱室,现浇箱梁采用梁格法建模,其端横梁承受腹板传递下的恒载主要包括箱梁自重与桥面铺装等。文献[5]对箱梁传递至端横梁的恒载分配方式进行了归类。
1.2.1 分配方式1
假设各个腹板将箱梁自重以及桥面铺装等恒载均匀分摊并传递至端横梁上,如计算公式(1)所示:
Ni=T/i
(1)
式中:Ni为第i个腹板传递的竖向荷载(腹板剪力);T为支座反力的合力;i为腹板数,i≥2。
1.2.2 分配方式2
按分梁面积来分配箱梁恒载,也即各个腹板传递的恒载按腹板所占面积之比进行划分,如图2所示,其计算如公式(2)所示:
Ni=T×(Ai/∑Ai)
(2)
式中:Ai为第i道腹板与翼缘所占面积,其中∑Ai为箱室总面积;其他符号同前。

图2 各个腹板占比面积
1.2.3 分配方式3
考虑箱梁扭转效应时,边腹板与中腹板的恒载分配将不均衡,依据工程设计经验,通常将中腹板与边腹板的恒载按照一定比例分配,一般中腹板为边腹板的1.2倍[5],如式(3)所示:
(3)
式中:Nk为中腹板或者边腹板传递的竖向荷载,其中k=1代表边腹板,k=2代表中腹板;uk为中腹板与边腹板的分配比例,其中u1=1,u2=1.2;其他符号同前。
1.3 恒载传递方式
在工程设计中,对现浇箱端横梁进行计算时,为保证计算结果合理可靠,通常单独建立端横梁计算模型,但是,采用端横梁模型计算时需要考虑箱梁纵向传递的恒载(包括自重与二期铺装),本文1.2节已经介绍了腹板承受恒载的分配比例,而本节主要介绍箱梁纵向恒载传递至端横梁上的几种传力模式,其分别有腹板集中力、腹板均布力、顶板均布力以及70%腹板集中力+30%顶板均布力[10]等,如图3所示。不同传力模式将对端横梁的受力性能产生影响。

图3 几种传力模式示意图
1.4 活载计算
建立单独端横梁模型来分析端横梁的受力性能时,活载主要通过在横梁影响线上布置活载系数来计算,如图4所示。其中横向加载时的活载系数q需要采用单箱梁模型单车道加载的方式获得。
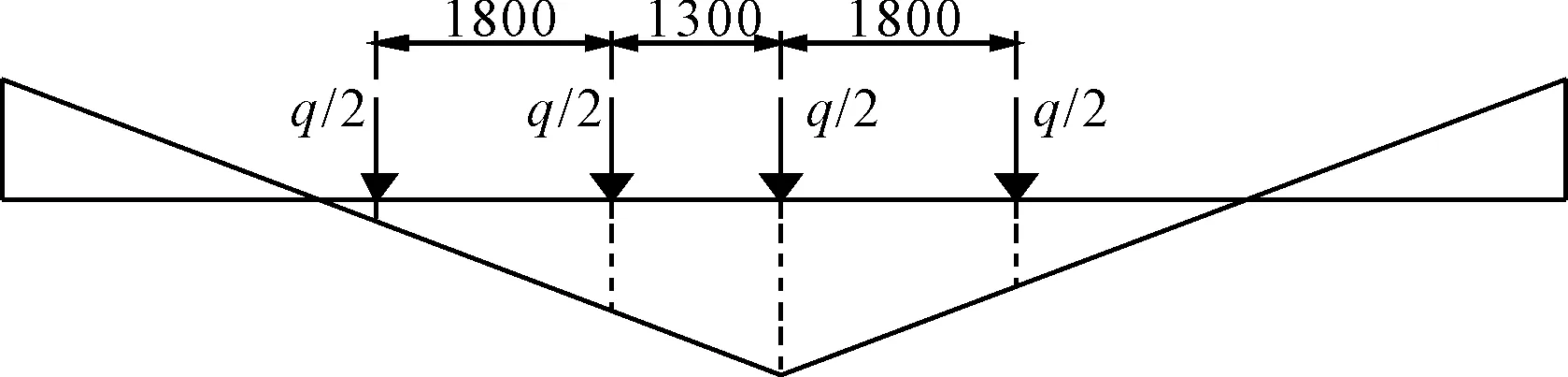
图4 横向活载系数布置示意图(单位:mm)
2 工程概况
本项目是在既有顺邵高速上增设某互通交叉处的一座主线桥,该主线桥上跨匝道且位于圆曲线段长=477.263 m,R=960.000 m路段内。经过经济性比选后,上部结构采用1×30 m PC简支现浇箱梁,下部构造采用U台配桩基,如图5所示。本桥左桥宽度12 m,采用单箱双室,右桥宽度16 m,采用单箱三室,主梁高1.8 m,箱梁悬臂长度2.0 m,顶板厚25 cm,底板厚25 cm,腹板宽45 cm,端横梁宽度1.5 m,箱梁顶底板平行,其中左桥箱梁截面如图6所示。
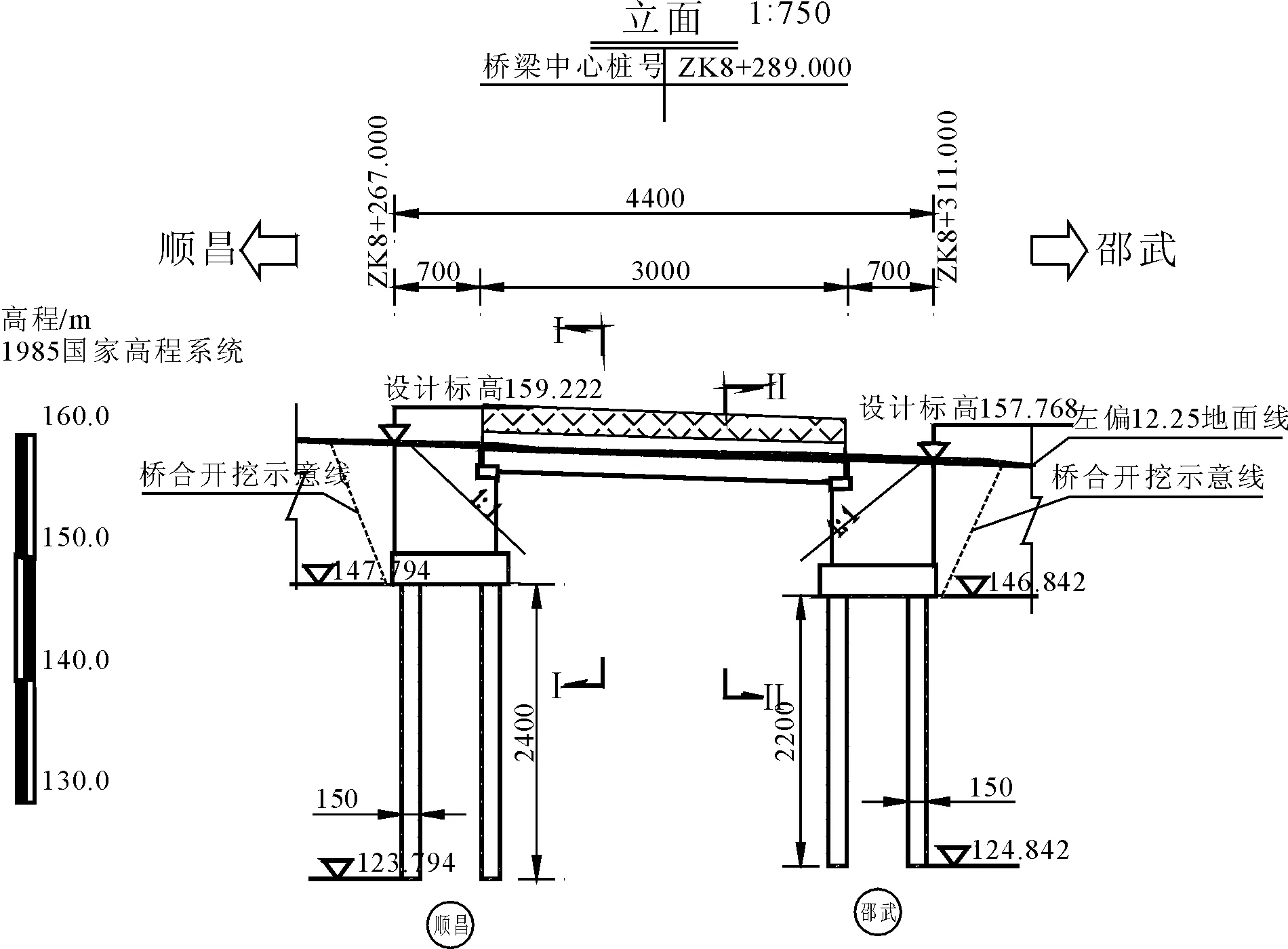
图5 桥型布置图(单位:cm)

图6 左桥箱梁横截面图(单位:mm)
3 有限元模型建立与验证
限于篇幅,本文仅对左桥进行分析,并采用桥博有限元软件建立左桥现浇箱端横梁模型,结构设计计算按照规范[9]要求,采用矩形截面的钢筋混凝土结构,荷载为公路-I级,结构重要性系数1.1,设计基准期100 a,环境类别I类,模型如图7所示。

图7 左桥箱梁端横梁模型示意图
本桥端横梁为钢筋混凝土结构,混凝土强度等级为C50,重度γc=26.0 kN/m3,弹性模量Ec=3.45×104MPa;钢筋等级为HRB400,弹性模量Es=2×105MPa,配筋如图8所示。桥面铺装共18 cm,其中10 cm为C50混凝土现浇层,8 cm为沥青铺装层,重度γa=24.0 kN/m3。按设计要求,在端横梁处设置两个支座,一端支座固定,另一端支座铰接,为简支梁受力条件。

图8 端横梁配筋图
在进行端横梁设计计算参数分析时,主要研究不同腹板恒载分配比例以及传力方式对端横梁受力性能的影响,具体数值分析工况如表1所示。

表1 端横梁数值分析表
说明:表中腹板传力方式中的百分数表示支座合力的占比。
通过梁格法建立箱梁模型可知,恒载作用下箱梁端横梁处支座反力的合力为4 668.1 kN,按文中1.2节恒载分配方式对其进行分配,结果如表2所示。由文中1.4节可知,横向布载时的活载系数通过建立单箱梁模型且采用单车道加载计算,其计算的横向活载系数为547。
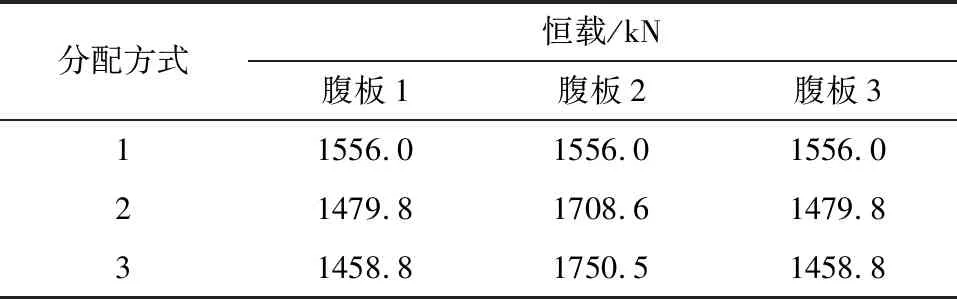
表2 恒载分配表
选取工况1-A作用下的有限元弯矩计算结果与简支梁理论计算结果进行对比可知,在跨中与支座位置处,有限元结果分别为1 011.4 kN·m与-1 400.4 kN·m,理论计算值分别为1 017.9 kN·m与-1 409.4 kN·m,两者基本接近,仅相差0.64%。同时,依据规范[9]可计算出端横梁的跨中下缘裂缝宽度为0.051 mm,而有限元计算结果为0.053 mm,两者相差3.92%。通过上述分析可知,有限元与理论计算值基本接近,为此,本文有限元分析结果是合理的。
4 恒载分配及传递方式对端横梁受力性能的影响
在验证有限元模型可靠的基础上,按照表1对端横梁的受力性能进行参数化分析。为便于对比,本文未提取端横梁悬臂部分结果,其悬臂计算结果将在桥面板分析中考虑。
图9为各工况之间的弯矩对比结果。由图9可知,不同工况作用下端横梁弯矩沿横桥向的变化规律基本一致,其中,在支点处产生负弯矩,在跨中处产生正弯矩。由图9还可知,在支座位置处,工况4-C作用下产生的负弯矩达到最大值-1 635.7 kN·m,在工况2-B作用下为最小值-1 331.8 kN·m,前者为后者的1.23倍。而在跨中截面处,在工况2-B作用下的正弯矩达到最大值1 316.5 kN·m,在工况4-C作用下的正弯矩为最小值233.4 kN·m,前者为后者的5.64倍。也即不同工况作用下,对端横梁跨中截面的正弯矩产生了较大影响,为此,验算端横梁跨中截面承载力极限状态时需要考虑不同恒载分配与传递方式对其产生的影响。

图9 各工况下的弯矩对比结果
图10为不同工况作用下横梁竖向位移的对比结果。由图10可知,不同工况作用下端横梁竖向位移沿横桥向的变化规律基本一致,但是,在跨中截面处的竖向位移相差较大,为工况4-D>工况3-B>工况2-B>工况1-B>工况3-A>工况2-A>工况1-A>工况4-C,其中在工况4-D作用下跨中竖向位移最大,其值为-0.216 mm,但是在工况2-B作用下,其值为-0.205 mm,两者相差5.09%。在工况4-C作用下跨中竖向位移最小,其值为-0.044 mm,即竖向位移最大值为最小值的4.91倍。同时,由规范[9]可知,钢筋混凝土受弯构件产生的最大挠度不应超过计算跨径的1/600,也即本文端横梁的挠度容许值为-10.33 mm。为此,当进行端横梁挠度验算时,采用工况4-D与工况2-B计算的挠度值即满足规范要求也较为安全。
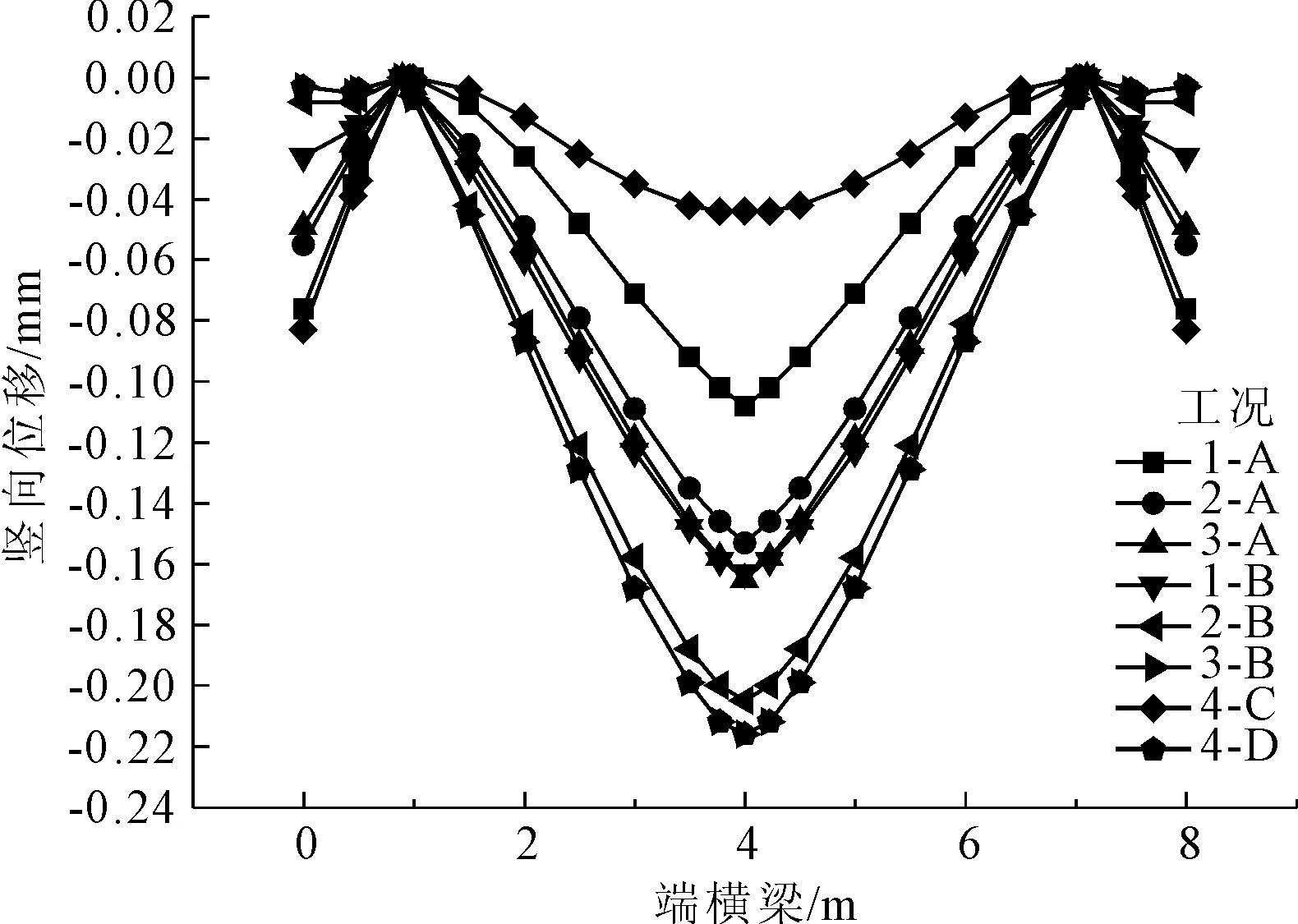
图10 各工况下的竖向位移对比
图11为不同工况作用下端横梁上下缘正应力的对比结果,其中,图11(a)为上缘正应力,图11(b)为下缘正应力,其正应力均为压应力且为标准组合作用下的结果。

图11 各工况下的上下缘正应力对比
由图11可知,在竖向恒载作用下,端横梁在跨中附近的上缘产生压应力,而在支座附近的下缘产生压应力。更细的由图11(a)可知,在工况3-B作用下,端横梁跨中上缘达到最大压应力4.85 MPa,在工况4-C作用下,跨中上缘达到最小压应力2.66 MPa,前者为后者的1.82倍;由图11(b)可知,在工况4-C作用下,支点下缘出现最大压应力4.16 MPa,在工况3-B作用下支点下缘出现最小压应力3.14 MPa,前者为后者的1.32倍。依据规范[9]可知,C50钢筋混凝土受弯构件的受压区混凝土边缘的压应力不大于25.95 MPa,虽然各方案作用下受压区混凝土的压应力存在较大差别,但是其远小于规范规定的限值,为此,在设计计算时,可不考虑上下缘压应力的影响。
表3为不同工况作用下端横梁最大裂缝宽度的对比结果。由表3可知,在工况4-C、工况4-D作用下,端横梁最大裂缝出现在支座上缘附近,而其他工况作用下,最大裂缝出现在下缘跨中位置。由表3还可知,在工况4-C作用下,上缘最大裂缝宽度达到了0.104 mm,在工况2-B、工况3-B作用下,下缘最大裂缝宽度分别为0.065 mm与0.067 mm,即上缘最大裂缝宽度为下缘的1.55倍。
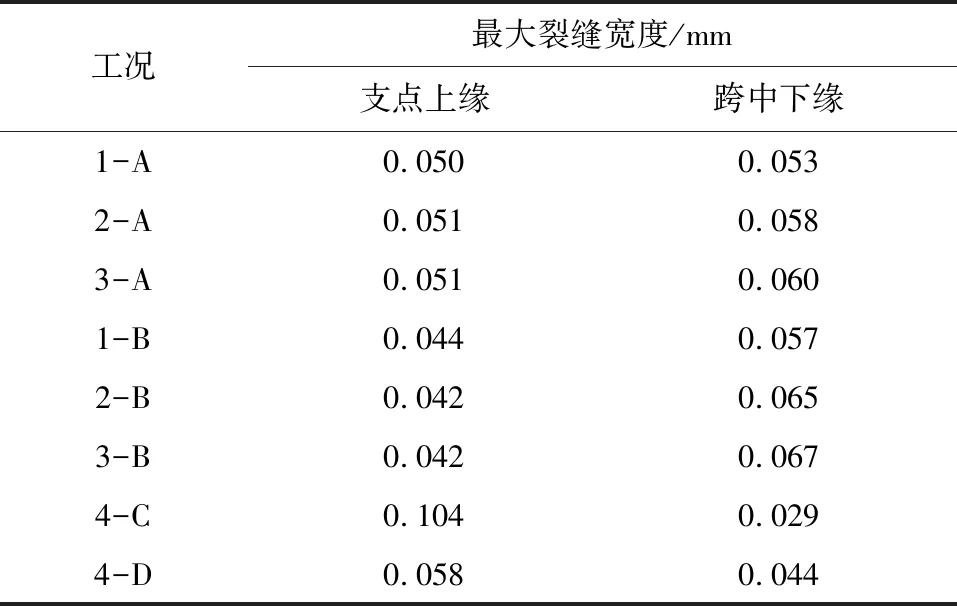
表3 各工况下最大裂缝宽度的对比
综上所述,不同的恒载分配与传力方式对端横梁内力、挠度、正应力以及裂缝宽度产生了较大的影响,尤其对端横梁跨中截面的正弯矩影响最大,影响值达到了5.64倍,另外,对跨中竖向挠度的影响次之,也达到了4.91倍,而对于正应力与裂缝宽度等差值基本控制在2倍范围内。
5 结 论
本文以某工程实例为背景,采用桥博有限元软件建立现浇箱端横梁模型,分析不同恒载分配比例以及传力模式对端横梁受力性能的影响,主要有以下几点结论。
(1) 当端横梁进行正截面抗弯承载力验算时,支点处计算建议采用工况4-C,即恒载通过均布力的方式作用在端横梁上,而跨中计算建议采用工况2-B,即恒载采用分配方式2且通过腹板均布作用到端横梁上。
(2) 当端横梁进行挠度验算时,跨中竖向位移计算建议采用工况2-B。当进行裂缝宽度验算时,支点附近最大裂缝计算建议采用工况4-C,跨中最大裂缝计算建议采用工况2-B。
(3) 综上所述,验算端横梁的承载能力极限状态与正常使用极限状态时,支点处采用工况4-C计算,而跨中处采用工况2-B计算,其计算结果安全系数较高。
