基于SPEI的甘肃省干旱特征分析

王阿静，王 伟

(1.永寿县水利管理站, 陕西 永寿 713400;2.武功县自来水公司，陕西 武功 712200)

干旱是一种频繁发生的自然现象，会对区域社会经济、生态环境、和人类生活造成极大的威胁[1-2]。随着全球气候变化加剧，导致部分地区干旱事件发生频率呈增加趋势[3-4]。因此需要对干旱的发生及变化特征进行深入研究。

由于对干旱研究的特点各异，干旱的分类也不尽相同，美国气象学会在总结各种分类的基础上将干旱分为4类：气象干旱、农业干旱、水文干旱和社会经济干旱[5]。气象干旱是引起其他干旱的前提，其他干旱都是气象干旱的影响结果，因此，准确监测气象干旱对于旱灾的预防、缓解等有重要意义。干旱指标是研究干旱的有力工具，其中，标准化降水指数(SPI)和帕尔默干旱指数(PDSI)是使用广泛的干旱指数。但是，SPI指数只考虑降水量的影响，忽略下垫面、作物及其他相关因素的影响，只能大致反映干旱发生趋势，不能准确反映某时段干旱发生程度[5]，PDSI指数对于不同区域、不同时间尺度的干旱监测对比性较差。Vicente-Settano[6]提出的标准化散发指数(SPEI)，其算法与SPI类似，而变量为降水(P)与潜在蒸散发(PET)的差值D，D表征某区域特定时间尺度下水量盈余或缺乏程度。SPEI指数基于水量平衡原理，同时又可表征不同时间尺度的干旱特征，自提出后便得到了广泛应用。

以往关于对干旱事件的研究侧重对单变量干旱特征的研究，然而，单变量干旱特征很难表征干旱事件变化规律。因此，完整地描述干旱事件对多个干旱特征变量进行联合，研究多变量干旱特征的发生规律。本文首先根据甘肃省25个气象站点的月降水、温度数据计算得到了1982年—2015年的月SPEI指数序列值，然后利用游程理论进行干旱识别，利用Copula函数构建干旱历时、烈度的联合分布，计算其联合概率分布状况及重现期，为甘肃省干旱预警提供科学依据。

1 数据与方法

1.1 数据来源

利用1982年—2015年间甘肃省地面气象观测站的月降水、平均温度数据，数据来源于中国气象数据网(http://data.cma.cn/)。选择研究区域内25个气象站点(见图1)。将干旱划分为轻、中、重旱3个程度。

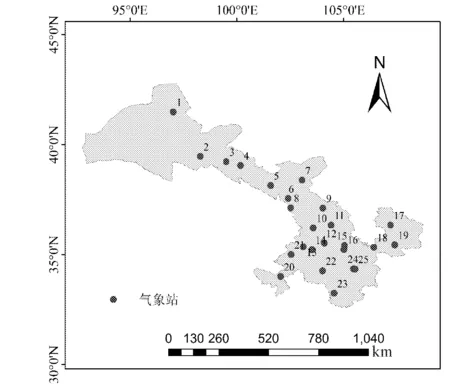
图1 甘肃省25个气象站分布

1.2 研究方法

1.2.1 标准化降水蒸散指数(SPEI)[7]

(1) 本文采用Thornthwaite公式计算潜在蒸散量：

(1)

式中：K为修正系数；T为月平均气温；I为年总加热指数；m是由I决定的系数。

(2) 逐月计算降水与潜在蒸散的差值：

Di=Pi-PETi

(2)

式中：Pi为月降水量；PETi为月潜在蒸散量。

(3)采用三参数的Log-logistic分布对Di进行拟合，得出累积概率函数：

(3)

(4)

式中：α为尺度参数;β为形状参数;γ为Origin参数;f(x) 为概率密度函数;F(x) 为概率分布函数。

(4)利用正态逆变换求出SPEI：

(5)

(6)

式中：P≤0.5 时，P=F(x)；当P>0.5 时，P=1-F(x)；C0=2.515517，C1=0.802853，C2=0.010328，d1=1.432788，d2=0.189269，d3=0.001308[7]。

对甘肃省25个气象站的气象数据进行处理，得到1982年—2015年的SPEI，利用1个月时间尺度的SPEI分析甘肃省干旱时空变化规律，并进行登记划分(表1)。

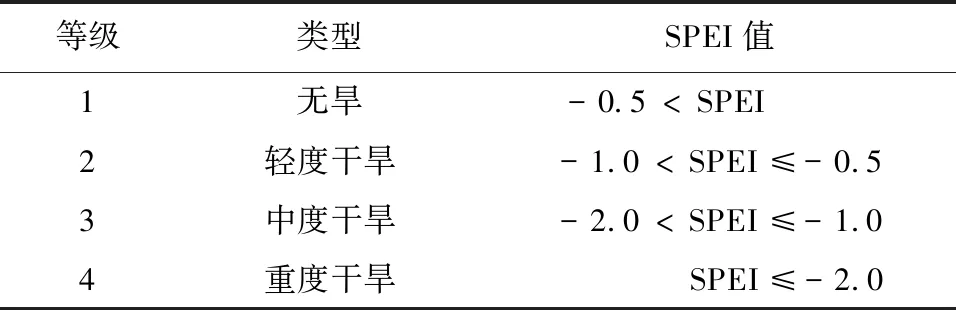
表1 标准化降水蒸散指数干旱等级划分

1.2.2 干旱识别

以游程理论为工具，从计算的SPEI 序列中识别出干旱历时和烈度2个特征变量。干旱历时表示一次干旱事件从发生到结束所持续的时间，干旱烈度为在该次干旱事件过程中SPEI累计值的绝对值之和，设定3个截断水平X0、X1和X2，干旱事件的识别过程为[1]：

(1)当SPEI 值小于X1时，则初步判定此月发生干旱。

(2) 对于干旱历时为1个月的干旱事件，当其SPEI值大于X2，则认为此月没有发生干旱，将其剔除。

(3)当相邻2次干旱过程的时间间隔仅为1个月，且该月内的SPEI值小于X0，则将这2次相邻干旱过程合并为1次干旱事件，干旱历时为两次干旱历时之和加1，干旱烈度为2次干旱事件的烈度之和，否则为2次独立的干旱过程。计算过程取X0=0，X2=-0.5，X1=-0.3。

1.2.3 边缘分布

干旱历时、烈度的边缘分布函数分别表示为FD(d)和FS(s)，干旱烈度的边缘分布类型选为伽马分布，干旱历时的边缘分布函数选为威尔布分布。

1.2.4 联合分布函数

Copula基于变量间的相关性对变量特征进行联合。干旱历时、烈度联合分布函数为：

F(d,s)=P(D≤d,S≤s)=C(FD(d),FS(s))

(7)

本文选择常用的Frank-Copula作为联接函数。

1.2.5 重现期计算

干旱历时和干旱烈度的单变量联合重现期为：

(8)

(9)

式中:T(d)和T(s)分别表示干旱历时、烈度的重现期；N为干旱系列长度，34 a；n为干旱事件次数，表示干旱事件发生的总次数。

两变量的联合重现期为：

(10)

2 结果与分析

2.1 干旱事件特征分析

根据游程理论提取出1982年—2015年间各个气象站点发生干旱事件的干旱历时、干旱烈度，统计出干旱事件的发生频次以及干旱等级，1982年—2015年间甘肃省出现的最低干旱事件频次为130次，最高150次，甘肃北部是主要的旱灾频发区，南部地区干旱发生频率相对较小(见图2)。而重旱发生频率较高的站主要集中在甘肃东部，最高为7次。

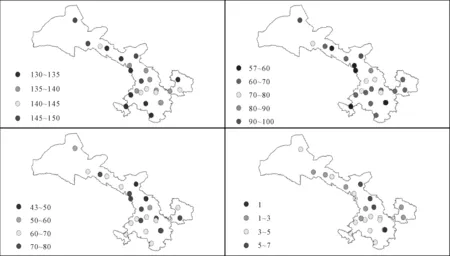
图2 1982年—2015年间甘肃省不同等级干旱发生频次空间分布

2.2 基于Copula的干旱事件联合分布

2.2.1 单变量线型拟合

对于干旱历时，通常会选用威尔布分布，对于干旱烈度，通常会选用伽马分布，本文以马鬃山站和酒泉站为例，分别对干旱历时、干旱烈度的拟合分布函数进行分析。结果表明，干旱烈度的拟合效果更好，理论分布与经验分布的匹配程度更佳，这主要是因为干旱历时重复点较多，导致其分布稀疏，使得理论配线效果不佳，但是仍能通过KS检验。因此，对干旱历时采用威尔布分布，对干旱烈度采用伽马分布进行配线(见图3、图4)。

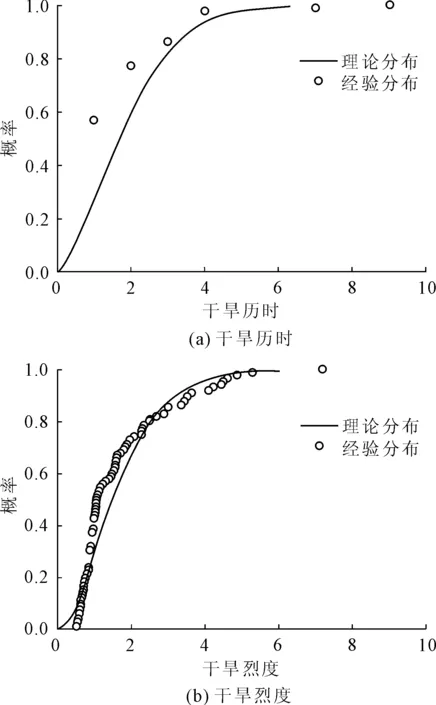
图3 马鬃山站干旱历时、干旱烈度经验分布与理论分布

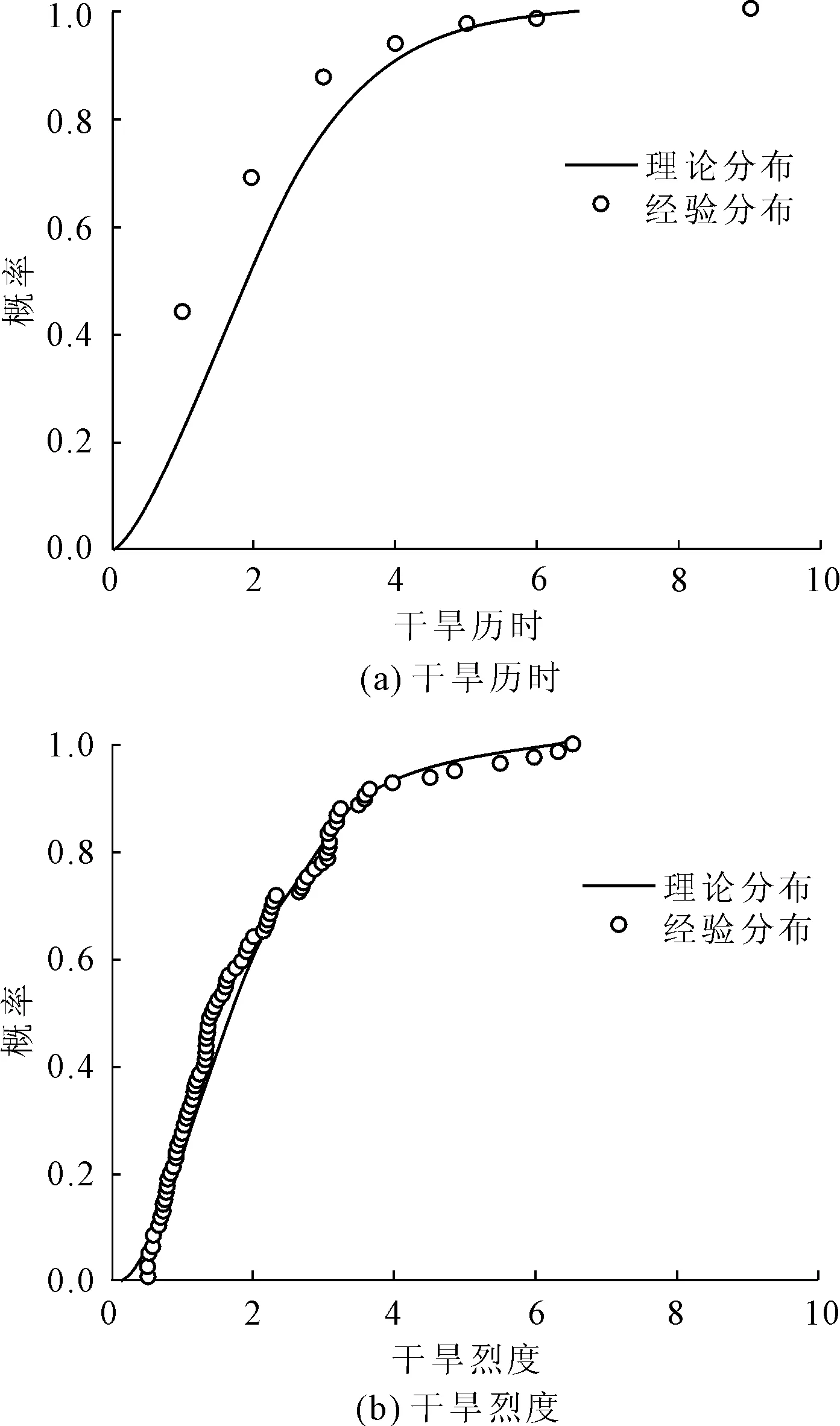
图4 酒泉站干旱历时、干旱烈度经验分布与理论分布

2.2.2 干旱历时和干旱烈度的联合概率分布

分别利用威布尔分布和伽马分布干旱历时、烈度配线，利用Frank Copula函数进行联合，如图5、图6所示，随着干旱历时、干旱烈度概率值的不断增大，累计概率的值也不断增大。表明随着干旱历时，干旱烈度的增大，其联合事件的发生概率也随之增大，马鬃山站与酒泉站干旱事件以干旱历时与干旱烈度同步的情况最多，长历时伴随着高烈度干旱情况。除此，也有短历时高烈度干旱事件发生，此类干旱事件的干旱烈度比较大，短时期内发生了严重的水资源短缺状况。

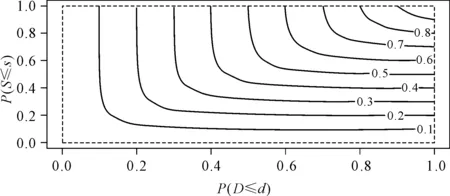
图5 马鬃山站干旱历时、烈度联合概率等值线图

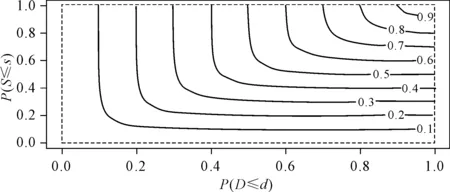
图6 酒泉站干旱历史、烈度联合概率等值线图

2.2.3 干旱历时和干旱烈度的联合重现期

以马鬃山和酒泉两个站点为例，单变量干旱事件(历时、烈度)的重现期随历时增长、历时增大呈增大趋势(见图7)，马鬃山站干旱历时为6个月时，干旱历时重现期超过80 a，酒泉站干旱历时为6个月时，干旱重现期仅为40 a。通过联合概率计算，得到了两站的干旱历时与干旱烈度的联合重现期(见图8)，当干旱历时、烈度达最大时，马鬃山站干旱联合重现期为5 a，酒泉站的联合重现期为4.5 a(见图9)。

马鬃山和酒泉站所在区域的联合重现期随历时和烈度的增加都呈增加趋势，酒泉站趋势变化更加显著，对不同干旱事件的重现期进行正确估计，可以为农业气象干旱预防治提供更加科学的指导[1]。

3 结 论

利用甘肃省25个气象站的月降水温度数据计算出了月SPEI系列数据，基于游程理论识别甘肃省在1982年—2015 年间的干旱事件的历时和烈度，利用Copula函数将干旱历时与烈度进行联合，分析联合累计概率和联合重现期，主要结论如下：

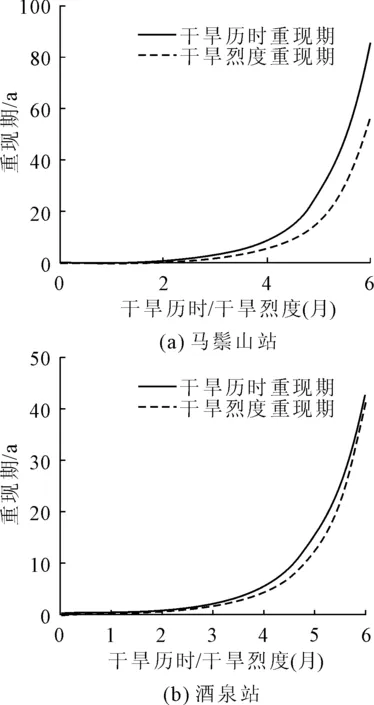
图7 马鬃山站、酒泉站干旱历时及干旱烈度重现期

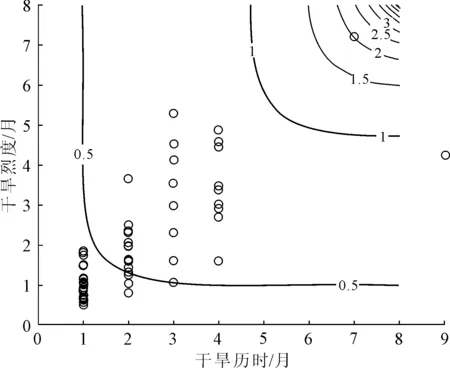
图8 马鬃山站干旱历时、烈度联合重现期

(1) 甘肃省出现最低干旱发生频次为130次，最高为150次，甘肃北部是主要的干旱灾害频发区，南部地区干旱发生频率相对较小。

(2) 采用Frank-copula函数对干旱两变量进行拟合，建立联合分布函数分析干旱特征变量的联合累计概率及联合重现期。

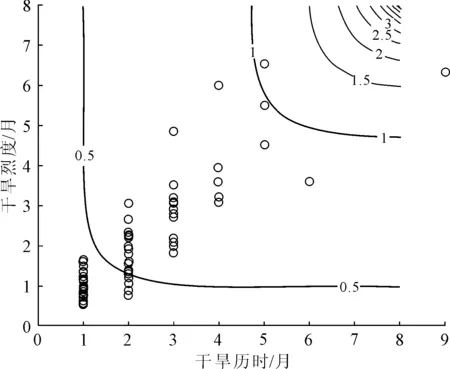
图9 酒泉站干旱历时、烈度联合重现期

(3) 随着干旱历时、烈度的不断增加，二者的联合累计概率和联合重现期也呈增加趋势。