极小子样加速退化试验数据可靠性评估方法
2020-10-28张海龙郭海亮
张海龙,郭海亮,孔 耀
(1.天地信息网络有限公司,北京 100041;2.中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
随着可靠性水平的不断提高,出现了许多高可靠性、长寿命的产品,如高可靠性的航天产品,其使用寿命和贮存寿命都比较长,要获得此类产品的寿命数据,对其可靠性进行评估,用基于概率统计理论的传统可靠性试验通常需要较长的试验时间或大样本量,且传统可靠性试验方法在工程上亦很难实现。文献[1-2]提出,对于很多产品,其性能参数随时间的推移会出现退化现象,因此可采用产品退化数据来进行产品的可靠性评估[3]。要评估产品总体的失效时间分布需要做大样本量的退化试验,但当样本量很小时,求解失效时间分布十分困难,此时就需要对试验样本量进行扩充。
对样本扩充问题主要采用Bootstrap法[4]和Jacknife法[5]。文献[6-7]提出,Bootstrap方法假设数据总体的分布未知,从已有数据样本中相继独立地抽取多个Bootstrap样本,利用这些样本对总体分布进行统计推断[8]。该方法很好地解决了试验样本量大于10的小子样试验评估问题,但对于样本量为1或2的极小子样试验问题,该方法就不适用了[9]。针对该问题,文献[10]提出了一种虚拟增广样本评估方法,具体做法是根据试验得到的单件样品的失效时间,利用类似产品的失效时间分布和标准差,将试验样本量进行虚拟扩充,然后再运用Bootstrap方法评估增广样本的分布函数。该方法的缺点是利用了类似产品的经验信息虚拟出样本数据,不能真实地反映实际产品的寿命分布特性。
本文提出了分段随机抽样的方法,对单一试验件的性能退化数据进行再抽样,生成新的退化数据时间序列,将小子样试验扩充为大样本量试验。然后对每一试验样本进行退化轨迹建模。本文采用Lu&Meeker[11]提出混合参数模型对退化轨迹进行建模,文献[12-13]对该模型进行了研究,并给出了模型参数的估计方法以及分布函数。本文以某航天器加速度计的加速退化试验为例,投入3个样品进行高温加速退化试验,评估加速度计在高温时的失效时间分布。结果表明,采用该方法扩充的新样本与原始样本有相近的退化趋势,没有出现较大的偏差,为解决小子样试验评估问题提供了一种可行思路。
1 样本扩充方法
针对极小子样试验,为了评估出产品的可靠性,得出失效时间分布,需要对试验样本量进行扩充。本文采用分段随机抽样的方法,对样件试验数据进行再抽样,生成新的试验数据序列,达到虚拟增加试验件的目的。
分段随机抽样是将测得的产品试验时间序列分成若干段,然后再分别对每段数据进行随机抽样。例如,时间序列:
A0={x1,x2,…,xm}。
将A0分成n(设m为n的整数倍)段,每段包含数据个数为n0=m/n,即:
A0={(x1,x2,…,xn0),…,(xm-n0+1,xm-n0+2,…,xm)}。
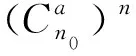
分段随机抽样的好处是,既扩充了试验样本量,又保持了原始数据的变化趋势,这在非线性变化的时间序列中非常重要。如果不采取分段随机抽样,而只是单纯地从原始数据中抽取a×n个数据,也就是说从原始数据中去掉m-a×n个数据,此时这m-a×n个数据有可能是一个相邻的数据段,这样就会造成抽样后数据的变化趋势与原始数据相差较大。例如,某时间序列X=[0,3.0,5.6,7.9,10.2,12.0,13.5,14.4,15.6,16.3],长度n=10,数据采集时间间隔为1 h。将该时间序列分为3段(不含初始点),每段3个数据,依次从每段中抽取2个数据,组成新的时间序列,共可得到27条抽样序列。分段随机抽样与非分段对比如图1所示,红线为原始时间序列的拟合曲线,蓝线为分段随机抽样后时间序列的拟合曲线,黑线为不采取分段随机抽样,而是随机去掉3个连续的数字(以去掉末尾3个数据为例)后的拟合曲线。由图1可以看出,未采用分段随机抽样的序列拟合曲线与原始序列拟合曲线偏差太大。
通过以上方法将极小子样扩充为大样本量后,运用混合参数模型对退化轨迹进行建模,求解失效时间的分布。
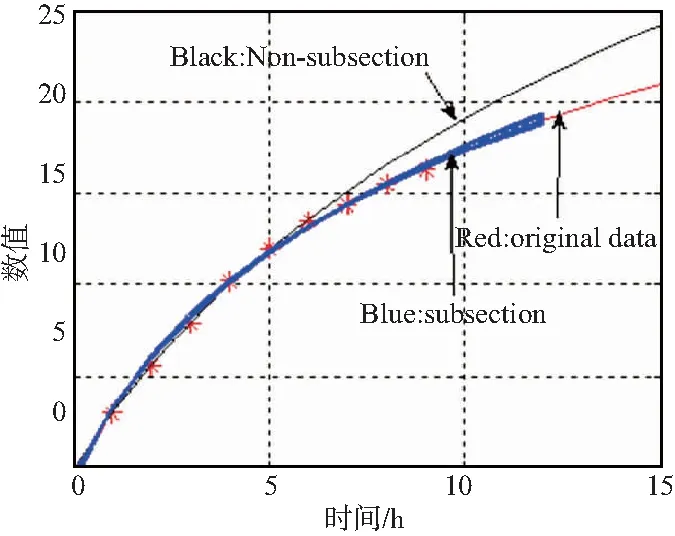
图1 分段随机抽样与非分段对比Fig.1 Comparison of subsection and non-subsection random sampling
2 混合参数评估模型
2.1 混合参数模型
加速退化试验过程中,环境应力对每一个试验件起到相同的环境影响,且每个试验件有其独立的特性,在对退化轨迹进行建模时应同时考虑固定影响因素和随机影响因素。因此本文采用混合参数模型对退化轨迹进行建模。文献[11]中给出了元件退化建模的一般公式。对于样本量为n的随机样本,设定在时间t1,t2,…,ts处测得性能退化数据,通常直到性能退化量x首达退化阈值D或时间达到ts,停止测量。第i元件在时间tj时的退化轨迹模型:
yij=η(tj;φ,θi)+εij,i=1,2,…,n,j=1,2,…,m,
(1)
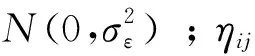
2.2 参数评估方法
基于两阶段法的模型参数估计方法,分为2个步骤。在第1阶段,对每个抽样元件的退化轨迹进行建模并估计轨迹参数,获得n组模型参数估计值。第2阶段,用第1阶段得到的模型参数估计值,来计算混合参数模型参数φ,μθ,Σθ。具体内容如下:
阶段1:
对每个抽样样本i(i=1,2,…,n),运用最小二乘法对(φi,θi)进行估计。最小二乘函数为:
(2)
第i个元件的测量误差εi的方差为:
(3)

(4)
(5)

阶段2:
(6)
(7)
(8)
式中,
2.3 失效时间分布
失效时间T的分布函数可以写为:
Pr{T≤t}=FT(t)=FT(t;φ,Gθ(·),D,η)。
(9)
当随机影响参数向量θ中只包含一个随机参数时,可以得到失效时间T分布函数的显式表达式。设η=φ+ϑt,θ~N(μ,σ2),退化失效阈值为D,则有D=η(T;φ,θ),此时:
(10)
则T的分布函数为:
(11)
当σθ<<μθ时,Pr(θ≤0)是可以忽略的,则式(11)改写为:
(12)
对于一些简单的轨迹模型,可以得到FT(t)的显式形式。但当随机参数多于一个时,问题就会比较复杂,很难写出闭式表达式。在此情况下,可以通过积分变换或其他方法找到T函数中随机参数的分布。文献[14-15]对这一问题进行了深入研究。通常需要估计数值结果,此时可以通过蒙特卡洛仿真得到结果。
3 应用实例
以加速度计的高温加速贮存试验为例,选取性能参数为标度因数(单位为ppm,即10-6),试验样本量为3,属于极小子样试验。试验中,温度设定为80 ℃,测量时间间隔120 h,试验终止时间2 160 h。初始时刻性能退化量为零,共测得19个数据,如图2所示。

图2 加速度计加速退化试验数据Fig.2 Accelerated degradation test data for accelerometers
根据文献[16-17],本文采用幂函数对加速度计退化轨迹进行建模,因此非线性混合参数轨迹模型为:
yij=φ1+θtφ2+εij,i=1,2,…,n,j=1,2,…,m,
式中,φ=[φ1,φ2]′;θ=[ϑ]′。
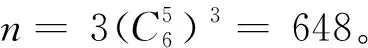
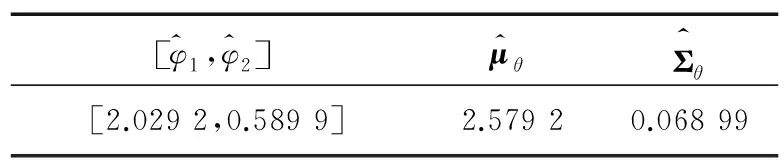
表1 参数估计值Tab.1 Estimated values of parameters
令失效阈值为300,T的累积概率分布曲线如图3所示。
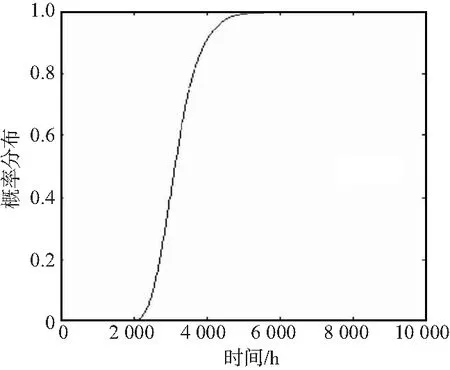
图3 失效时间累积概率分布曲线F(t)Fig.3 The failure time cumulative probability distribution curve F(t)
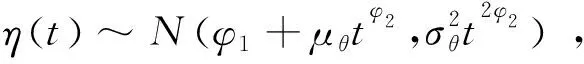
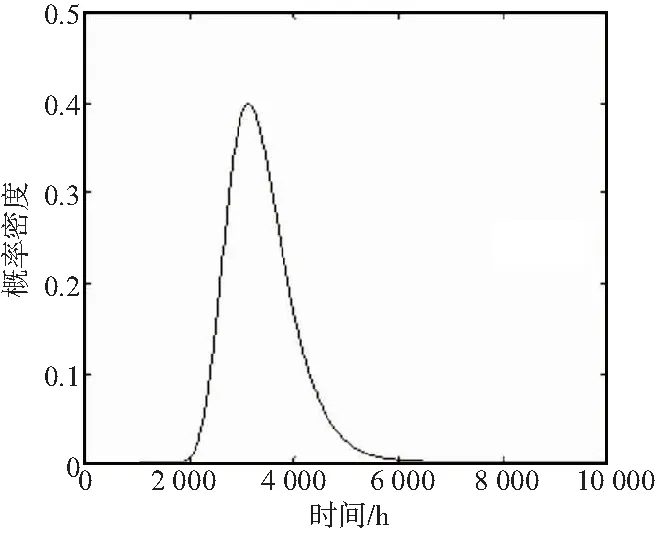
图4 失效时间概率密度曲线f(t)Fig.4 The failure time probability distribution curve f(t)
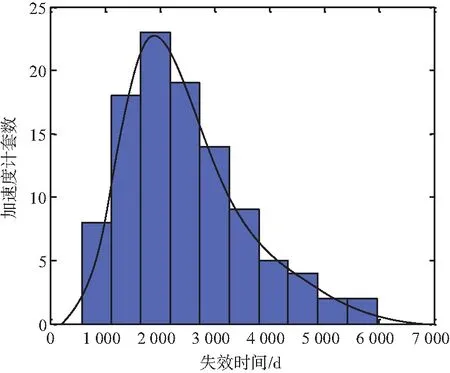
图5 自然贮存加速度计失效时间直方图Fig.5 The histogram of failure time for accelerometers with normal storage
4 结束语
针对极小子样加速退化试验,提出了基于分段随机抽样的再抽样方法,通过实际应用可得出,该方法可对极小子样加速退化试验样本进行有效地扩充,同时未改变退化轨迹的趋势;评估得到的失效时间分布与正常应力下的产品失效时间分布接近,保证了加速退化试验失效机理的一致性。
