水资源开发利用生态补偿研究——以重庆市万州区为例

刘加伶，时岩钧，刘冠伸

(1.重庆理工大学 计算机科学与工程学院，重庆 400054； 2.重庆理工大学 管理学院，重庆 400054)

1 研究背景

为了适应我国流域资源的开发速度与水资源的公共物品属性，政府需要建立流域生态补偿机制，以提供足够的流域生态服务，保证流域的可持续发展。建设长江经济带是我国重要的经济发展战略之一，流域境内水体环境恶化和生态污染加剧的现象，已成为制约绿色发展的重要阻碍[1]。因此建立长江经济带绿色发展体系，实现水资源可持续利用和绿色发展，是长江经济带经济发展的战略选择，也是解决资源环境困境的必经之路。近些年来，学术界对于水资源生态补偿有着不同层次的研究，从研究内容来看，主要集中在水资源生态补偿的定义[2]、上下游流域生态补偿模型的构建[3]、水资源生态补偿效率的测度[4]、水资源生态补偿量化标准[5]、水资源保护与政府财政之间的关系[6]以及水资源安全[7]等方面。研究对象主要为流域水资源生态补偿[8]、水资源生态补偿参与者利益诉求[9]等。研究区域一般为经济发达的长江流域[8]与生态环境较为脆弱的西北地区[10]。长江经济带作为国家目前重点开发建设的经济区域，资源与经济发展矛盾尤为突出，重庆市万州区更是其中的典型。因此，建立该区域的水资源开发利用生态补偿机制，对于地方经济发展有着重要的意义。以上的研究无疑对现今水资源生态补偿机制的构建有着巨大的推动作用，但也存在一些不足，比如：

(1) 研究对象选择片面，忽视了当前我国经济开发区建设进程中，中央作为强互惠者参与治理的客观情况，以及区域产业升级时地方政府监管力度不足的现象。

(2) 现有的研究方法主要是基于建立水资源生态补偿模型，大多数模型只是基于过往数据对水资源生态补偿各方的意愿进行数值分析,鲜少与实证案例的仿真工具相结合。

有鉴于此，本文构建了基于中央-当地政府-地方企业的三方演化博弈模型，并基于系统的动力学模型，以重庆市的万州区生态补偿案例为研究对象开展实证分析。

2 基于演化博弈的水资源生态补偿关联主体的利益均衡

2.1 中央与地方政府监管博弈分析

长江经济带作为我国近些年来经济开发与转型的重要区域，在水资源利用中多出现资源枯竭、利用过度等情况，为此本研究对长江经济带的实际情况进行了具体分析。长江横跨11个省、市、自治区，流域的上下游之间经济发展差异较大，部分地区的水资源基础设施建设不完善，因此在现阶段长江流域水资源生态补偿中需要中央参与，地方与企业共同配合的三主体的治理机制。

当前我国环境治理已经逐渐从中央负责转变到地方负责，地方政府也因此对辖区的环境治理有着更大的责任，但中央与地方政府仍在水资源治理责任判定、收益分配、开发目标等方面存在着分歧：中央更多是强调以绿色发展为前提来发展经济，实现水资源的可持续发展；地方政府更多是强调自身的短期利益，关心资源的开发给地方所带来的经济利益和增加就业量。在经济发展与政治声望的双重驱动下，地方政府更倾向于在现有工业基础上加速发展，在这个过程中对环境与企业的监管相对宽松。因此，落实到具体的水资源开发进程中，地方政府往往就会降低环境保护在经济发展中的优先级别，利用水资源的负外部性效益以及相关法规的漏洞与中央进行博弈，以达到加速地方经济发展的目的。

2.1.1中央政府与地方政府博弈模型

假设在中央政府与地方政府的水资源生态补偿博弈中，双方都会有执行和不执行两种行为选择。其中，中央政府的策略集为(监管，不监管)政府行为，地方政府的策略集为(执行，不执行)相关政策法规，据此构建出演化博弈矩阵。同时，设中央政府改变采取监管措施的概率为X，不采取监管措施的概率为1-X；地方政府执行措施的概率为Y，不执行措施的概率为1-Y。基于此，作出如下假设。

(1) 假设1。当中央政府选择监管地方政府行为时，监督成本为C1,因政策执行对地方环境的社会与经济效用附加值记为G。

(2) 假设2。地方政府执行生态补偿政策时的基本效用为L1,不执行生态补偿政策的效用记为L2，执行所付出的生态补偿成本记为CL；同时会获得中央政府的政策支持资金TC,不执行生态政策会有罚金F。

(3) 假设3。在中央与地方政府博弈中因其为从属关系，所以会存在一个强互惠者[14]，即中央政府。作为强互惠者的中央政府，当选择监管政策实施而地方政府消极执行时，可以运用行政手段对相关责任人进行惩罚，此时中央政府与地方政府各获得U1、U2单位负效用。同理，当中央政府不进行监管，地方政府主动实施生态补偿行为时，中央政府与地方政府各获得U3、U4单位正效应。在此基础上来构建此次博弈的支付矩阵，如表1所列。

表1 中央政府与地方政府的生态补偿支付矩阵Tab.1 Phase payment matrix of government and enterprise in green development

基于上述分析，可以构建博弈双方的收益期望效用函数。其中，中央政府选择监管与不监管时的期望效用表达如下：

(1)

(2)

根据Malthusian动态方程[15]，策略变化率等于微分方程，以此可以得到双方演化稳定策略的复制动态方程，进而求出企业与政府之间的演化稳定策略。

中央政府实行监管措施的复制动态方程以及一阶导数为

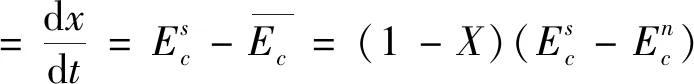
=X(1-X)(F-CI-U1+TC-YF-

YTC-YU3)

(3)

F′(c)=(1-2X)[F-CI-U1+TC-YF-

YTC-YU3]

(4)

当F(c)=0时，两种群体采用不同策略的比例达到稳定状态。此时求得的中央政府稳定点的解为

同理，得到地方政府选择执行政策与不执行政策的期望效用函数为

TC+U4)

(5)

(6)

地方政府的期望效用函数效用为

(7)

地方政府实行监管措施的复制动态方程以及一阶导数为

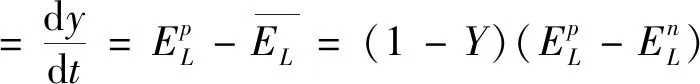
=Y(1-Y)[XF+XTC-XU4+L1-

L2+U4+U2-CL]

(8)

F*(L)=(1-2Y)[XF+XTC-XU4+L1-

L2+U4+U2-CL] (9)

当F(L)=0时，两种群体采用不同策略的比例达到稳定状态，此时求得的中央政府的稳定点的解为

2.1.2中央政府与地方政府的演化稳定分析

基于以上分析，构建了雅克比矩阵来进行局部均衡点稳定分析，旨在测验该博弈系统的稳定状态。式(3)和式(8)的行列式与迹所构建的雅可比矩阵为

(10)

并依照矩阵的局部分析法，对均衡点进行稳定性分析，具体如表2所列。

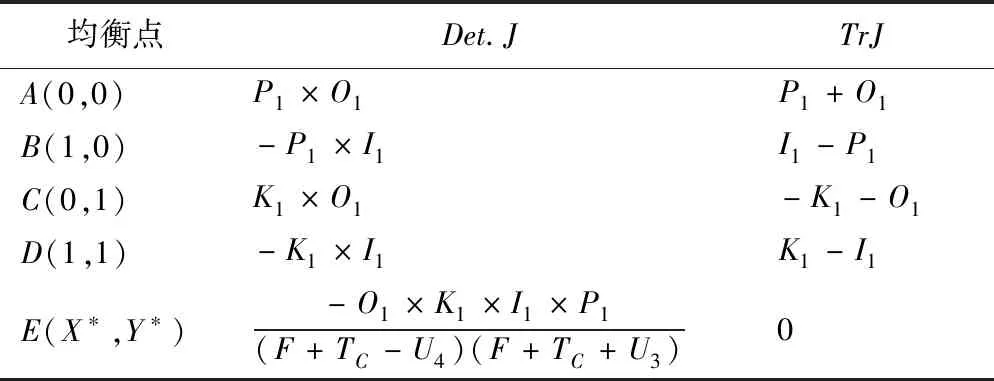
表2 中央与地方博弈雅可比矩阵Tab.2 The central and local game Jacobi matrix

为了简化表达，设定：P1=F-CI-U1+TC，O1=L1-L2+U4+U2-CL，K1=CI+U1+U2，I1=F+L1-L2+TC+U2-CL。在中央政府与地方政府的博弈中，最优解是(不监管，执行)组合，即中央政府不实行监管政策，地方政府自觉执行水资源生态补偿制度。在最优解条件下，已知K1>0,对参数P1、O1、I1进行讨论，判断Det.J、TrJ的符号(见表3)。

表3 中央政府与地方政府局部均衡点稳定性分析Tab.3 Stability analysis of central and local equilibrium points

由表3可以看出：以上两种情况可以达到(不监管，执行)的最优策略；其中，P1正负值不限制，而O1、I1的值需要大于0，所以可得：

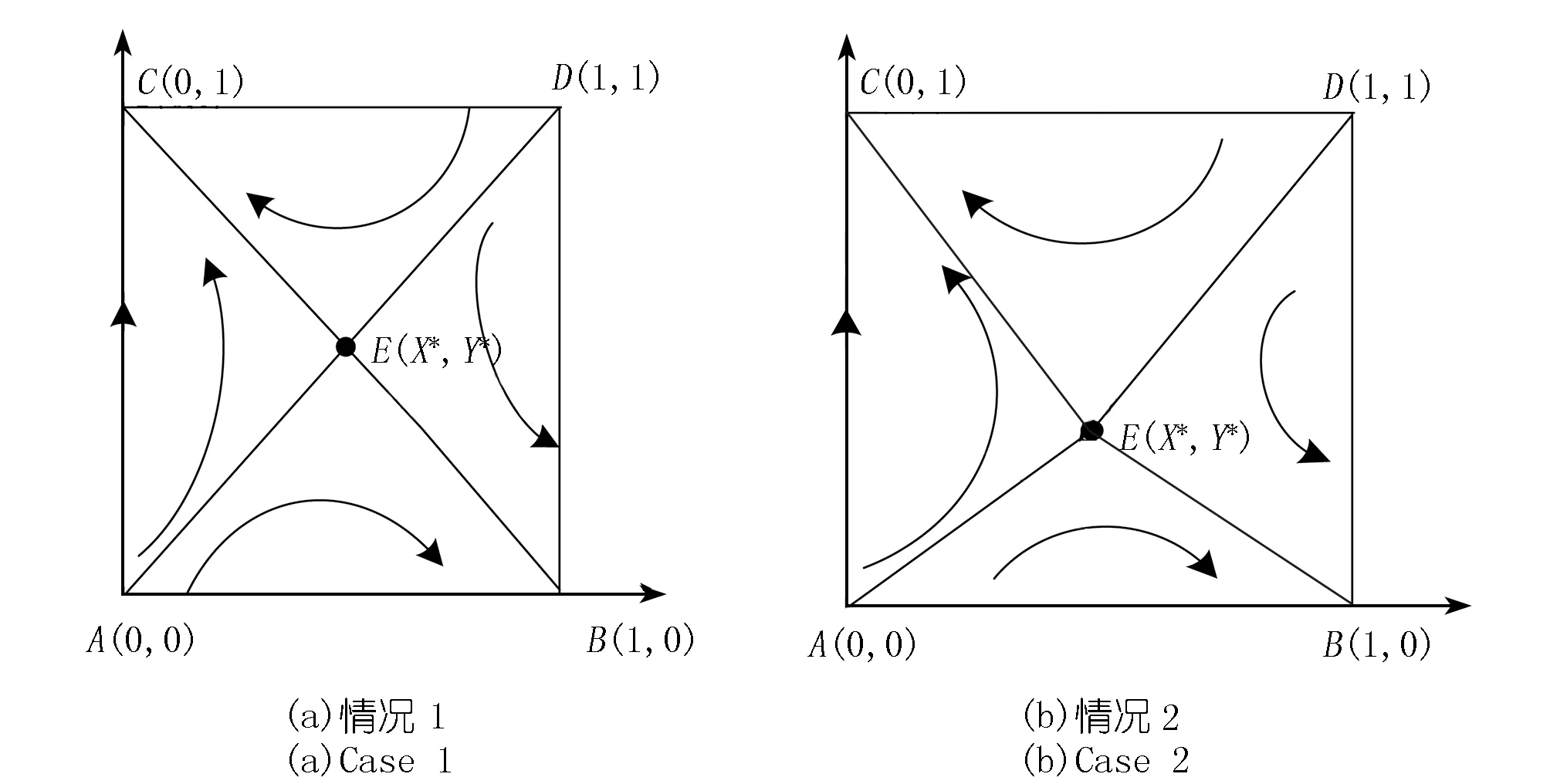
图1 中央政府与地方政府博弈行为相位图Fig.1 Phase diagram of game behavior between central and local governments

2.2 地方政府与当地企业的监管博弈分析

在现阶段长江流域水资源的生态开发与补偿中，地方政府与企业因利益诉求而存在着分歧，双方在博弈中既有合作也有矛盾。一方面，当地政府与企业的需要是共同合作，政府希望通过建立经济开发区来增加税收与就业岗位，企业也想通过与政府的合作得到政策优惠；另一方面，企业出于长远发展与声誉的考虑，有较强的积极性来升级技术保护水资源。可是仅依靠这些并不能完全使企业与政府之间的利益达到均衡，势必有些企业为了追求经济利益最大化，会不按章办事或买通政府进行寻租行为。地方政府作为当地利益的维护者，将会对这类行为进行监督与整治，保持当地经济与环境协调发展的平衡，政企双方基于不同的利益诉求进行博弈，这是双方博弈的基础。

2.2.1地方政府与当地企业博弈模型

在长江经济带水资源开发中，地方政府与当地企业博弈中既有合作又有矛盾。其中，地方政府的策略集为(监督，不监督)，当地企业的策略集为(治理，不治理)。根据相关政策法规，构建演化博弈矩阵，同时设地方政府改变采取监督措施的概率为α，不监督措施的概率为1-α；地方企业治理的概率为β，不治理的概率为1-β。基于此，可以作出如下假设。

假设1。当地方政府的监督成本为CG，地方政府进行监管与不监管的收益分别为R1和R2(R1>R2)，在企业不履行治理责任的情况下，地方政府需要支付额外治理成本为CE。

假设2。企业治理时投入的成本是CE，由此可以收获到企业的良好声誉成本X1，如果不治理，将会收入到地方政府的罚金H；企业执行与不执行治理政策的收益分别为D1和D2(D1>D2)，将企业每年固定要缴纳的税收记为TE，由此可以构建地方政府与企业收益矩阵，如表4所列。

表4 地方政府与企业的生态补偿支付矩阵Tab.4 Ecological compensation payment matrix of local governments and enterprises

政府与企业的期望效用函数效用分别为

(11)

(12)

此时，地方政府实行监管措施的复制动态方程以及一阶导数为

H-CG+TE-βH)

(13)

企业实行治理措施的复制动态方程以及一阶导数为

X1-CE+αH)

(14)

2.2.2地方政府与企业的演化稳定分析

根据以上分析结果，构建了雅可比矩阵对均衡点进行稳定性分析，如表5所列。

表5 地方政府与企业博弈雅可比矩阵Tab.5 Local and corporate game Jacobian matrix

为了简化表达，设：P2=R1-R2+H-CG+TE，O2=-H，K2=R1-R2-CG+TE，I2=D1-D2+X1-CE+H。在地方政府与企业的博弈中，最优解是(监督，治理)组合，即地方政府实行监督政策，企业自觉进行生产方面的生态治理，维持水资源可持续发展。地方政府的行政责任与中央不同，在地方发展中往往要承担更多的具体事务，比如监督政策实施与监管企业行为，以此来树立良好的政府形象。同时，企业也会通过实施水资源生态补偿来得到地方政府的财政补贴和当地居民的支持，从长期的角度来看，一个良好的生态环境也有利于企业的发展。这种地方政府适当监管与企业积极治理，是符合绿色发展理念行为的最优解。在此条件下，对参数P2、O2、I2、K2进行讨论，判断Det.J、TrJ的符号，有两种情况符合其演化博弈的最优策略，具体情况如表6所列。

表6 地方政府与企业局部均衡点分析Tab.6 Local and enterprise local equilibrium point analysis

由表6可知：演化博弈中想要达到(监督，治理)的情况，各参数中O2可正可负，P2>0，O2>0,K2>0，从而可得:P2=R1-R2+H-CG+TE、K2=R1-R2-CG+TE、I2=D1-D2+X1-CE+H。由此可知，增加R1-R2、H、TE、D1-D2、X1的值，减少CG、CE的值,可以使博弈模型更快达到稳定点；如图2的情况1和情况2所示，地方政府与当地企业在博弈中有更大可能达到I(1,1)点，即(监督，治理)这一最优策略。这也表明：对地方政府而言，要减少监管成本并增加监管后的既得利益，比如监管罚金、环境税收等；对企业而言，要激励其进行生态治理，减小企业生态治理成本，提高企业进行生态治理后的利益，从而有利于达到均衡策略的最优条件。

图2 地方政府与企业博弈行为相位图Fig.2 Phase diagram of game behavior between local governments and enterprises

3 水资源生态补偿关联主体利益均衡的实证

3.1 关联主体生态补偿分析

本研究以重庆市万州区为例进行实证分析。万州区作为渝东北重要的工业、商业、交通城区，在长江经济带建设中具有极其重要的位置。近年来，随着重庆市产业结构的升级，万州区政府着手于建设经济开发区，开发区内多为化工企业，对经济发展起到了一定的推动作用。然而在发展过程中，有些化工企业刻意地压缩本该用于治理排污的费用，导致工业废水不经处理而流入河流中；此外，万州区政府对水资源开发过程中的环境监管意愿不强。以上诸多因素导致了万州区水资源污染严重，长此下去，将会对长江沿岸以及长江中下游地区的生态环境造成不良的影响。针对上述情况，重庆市万州区人民政府及时反应，编制了《万州区贯彻落实水污染防治行动计划工作方案》，开展万州区的环境治理与水资源生态补偿工作。但是由于在水资源生态补偿中各利益主体的复杂性，需在实地调研与数据统计的基础上对案例中各方的行为进行分析。因此，本研究对重庆市万州区环保局以及相关工业园区进行了专访，对比水资源生态补偿的案例进行实证分析，与上述演化博弈中各利益主体之间的行为选择进行比较。采用贾舒娴[14]等对生态补偿前后收益的估算方法，将重庆市万州区生态补偿前的收益以2014年进行计算，开始的收益用2016年的数据进行测算，长远收益则采用2018年的数据来表示。

3.2 参数测算与估值

3.2.1中央政府和地方政府博弈的参数测算与估值

(1) 重庆市万州区中央政府的政策支持资金TC用生态价值当量法[16]为基础进行测算，其公式表达如下：

Q=∑Q(f,g,c,w,d,r)=∑sj×ej

(15)

Q=sf×fe+se×ge+sc×ce+sw×we+

sd×de+sr×re

(16)

J=Q×U×L

(17)

TC=Y=J-(D-I)

(18)

上述公式中:Q为重庆市辖区内生态价值总量，f、g、c、w、d、r分别为区内各湖泊、森林、农田以及湿地等生态分区的生态价值当量，sj为重庆市辖区生态系统的总面积，ej表示其中某一生态系统所对应的生态价值当量，J为重庆市生态经济价值，U为重庆市一个生态服务价值当量因子所对应的经济价值量，参考2014年刘春腊等[16]所测算的中国各省市生态价值当量值，取值为305.4 hm2，将调整系数L设为1，Y、D、I分别为重庆市生态经济剩余价值、预计治理污染的投入以及实际治理污染的投入。最后，得到中央政府对重庆市的生态补偿资金与财政转移支付资金TC约为40.860亿元。

(2) 地方政府不执行政策支付的罚金F，在重庆市万州区案例中，当地政府在环境恶化后积极实行监管与治理政策，此时地方政府所支付的罚金为0。在其他案例查询中，中央政府一般很少直接对地方政府实施罚款，多是采用通报批评或问责官员等方式，设F值为0。

(3) 重庆市执行生态补偿效用的收益，借鉴贾舒娴等的测算方法[14]，2016年全国财政收入同比增长7.4%，重庆市财政收入同比增长10.8%。重庆市2016年高于全国财政的增长率的部分，反映了地方政府执行生态补偿政策后的收益情况，则L1=L2×(1+10.8%-7.4%)=2 227.9×103.4=2 294.737亿元。此外，公式中的其他数据如表7所列。

表7 中央政府与地方政府博弈中参数定义及统计说明Tab.7 Parameter definition and statistical description in the model 亿元

3.2.2地方政府和当地企业博弈的参数测算与估值

当地企业的生态建设与补偿成本CE主要包括2个部分：一部分是因排污问题引起的水资源污染进而导致当地居民生产与生活不便而应付出的生态补偿成本；另一部分为河流治理及环境恢复费用。主要通过以下方法进行测算。

(1) 企业对居民身体健康的补偿金额CDA，主要采用修正人力法与医疗费用法测量，水污染对人群健康造成的经济损失包含每年早逝人群的健康损失而导致的经济价值、因病引起的病假损失及医疗费用两部分组成。

CDA=V1+V2

V1=早逝例数×VSL

(19)

VSL(每例早逝的统计生命价值)=GDPcs×

(20)

V2=住院病例×患者的误工天数×

(人均收入+每日医疗费用)=132×10×

(120+90)=27.72万元

(21)

上述式中：V1为万州区水资源污染给当地居民造成的经济损失及居民健康成本；GDPcs采用2014基准年计算，万州区的人均GDP为5.190万元；i为万州区的经济增速6.8%；g为万州区的贴现率以3 a以上银行贷款计算，为5.74%；n为早逝损失的工作年数，借鉴胥卫平等[17]研究成果测算的因水污染而损失的工作年数约为14 a。同时，根据卫生统计与服务部门的资料而获取的医疗费用及病例调查表明：2014年，万州区可查病例记录约为132例，早逝病例约为4例，平均住院天数为10 d，每人医疗费用约1 000元。所以CDA=249.07+27.72=276.79万元。

(2) 对于河流治理及环境恢复费用，主要是采用实际调研以及运用影子价格来测算因水资源污染所要付出的社会、经济及生态环境价值。

万州区工业开发园区产生的占地面积为33.5 km2，截至2016年，初步测算万州区居民每人用水的经济费用为1元，1 a共需要1.5亿元；同时，工业用地并占据了农耕用地15.0 km2,结合自然以及当地人文经济因素，借鉴于相关的耕地价值计算公式，经计算得到万州区的补偿标准为152.63万元/hm2，共计22.89亿元。基于以上公式计算出企业的生态建设与补偿成本CE为24.39亿元。

(3) 企业执行与不执行生态治理政策的收益为D1和D2(D1>D2)。

2015年，重庆市万州区工业园区整体的企业营收收入为521.00亿元；2016年，万州区工业园区企业营收收入为621.00亿元，年收入增长率为12%，全国工业园区平均增长率为6%，则2016年万州区工业园区相对于全国工业园区而言的营业收入增长率的增加值即表示万州区工业园区进行生态补偿前后的收益，亦即D1=D2×(1+12%-6%)=521×106%=552.26亿元。

博弈公式中的其他数据如表8所列。

表8 地方政府与当地企业博弈中参数定义及统计说明Tab.8 Parameter definition and statistical description in the model 亿元

3.3 生态补偿中各方利益主体的实证模拟结果

水资源生态补偿系统动力学模型仿真，主要是验证上述演化博弈模拟结果的正确性并进一步预测博弈主体行为的概率变化率。因此，构建系统动力学模型来进行仿真研究，主要设计思路是拟通过水资源生态补偿中央政府、地方政府、当地企业博弈的相互制衡影响关系来搭建SD模型，如图3所示。

图3 水资源开发生态补偿系统动力学图Fig.3 Dynamics diagram of ecological compensation system for water resources development

结合博弈过程中的复制动态方程，以及表7和表8中所列出的案例数据与部分测算值，运用Vensim.PLE软件，对水资源生态补偿中各方利益主体的动态博弈行为进行仿真模拟。三方主体行为的动态演化结果分别如图4和图5所示。

上述案例中，中央与地方政府博弈时的具体实证数据为F-CI-U1+TC>0,L1-L2+U4+U2-CL>0,F+L1-L2+TC+U2-CL>0，满足表3中局部稳定点的情况1。由图4可知：此时在中央政府与地方政府的博弈中，实现中央政府不监管，地方政府主动实施生态保护策略，达到了帕累托最优策略(不监管，实施)，这是因为在此次博弈中，地方政府不执行政策支付罚金F较低时，获得的中央财政转移补贴资金较多；同时，在执行政策后地方政府得到的收益较大，能够缓和其所付出的生态治理成本，使地方政府有更高的积极性来进行环境监督与治理工作。由图4还可以看出：地方政府实施政策曲线的斜率要大于中央政府实施政策的斜率，表明在双方的博弈过程中，中央政府并不会直接放弃对地方的监管，而是具备一个考察过程。因此，地方政府有更强烈的积极性实行治理行为。

图4 中央与地方政府博弈行为博弈仿真Fig.4 Game simulation of game behavior between central and local governments

根据图5可知：在地方政府与当地企业的博弈过程中，可以达到地方政府监督，企业自觉治理这一最优均衡策略。算例中具体数值符合表6均衡点分析中情况1的数值，即P2>0,O2>0,I2>0，K2>0可以在演化博弈中达到(监督，治理)这一最优策略。这是因为在该案例中，地方政府可以通过高效率的监管方式取得良好的成效，虽然所征收的资源税不高，但因此获得了较好的民间声誉与地区长期发展的可能性。对企业而言，虽然短期利益受损，但是可以获得足够弥补其损失的长期的经济收益与心理收益，并使企业的负外部性效益降到最低，长远来看，有利于企业在当地的发展建设。

由图5还可以看出：企业实行治理措施曲线的斜率要高于当地政府实施监督措施曲线的斜率。这就表明：在双方的博弈中，地方政府出台的政策与具体落实监督是一个平稳的过程，而当地企业对于政策变化表现出的较为敏感，会较快达到合作路径。

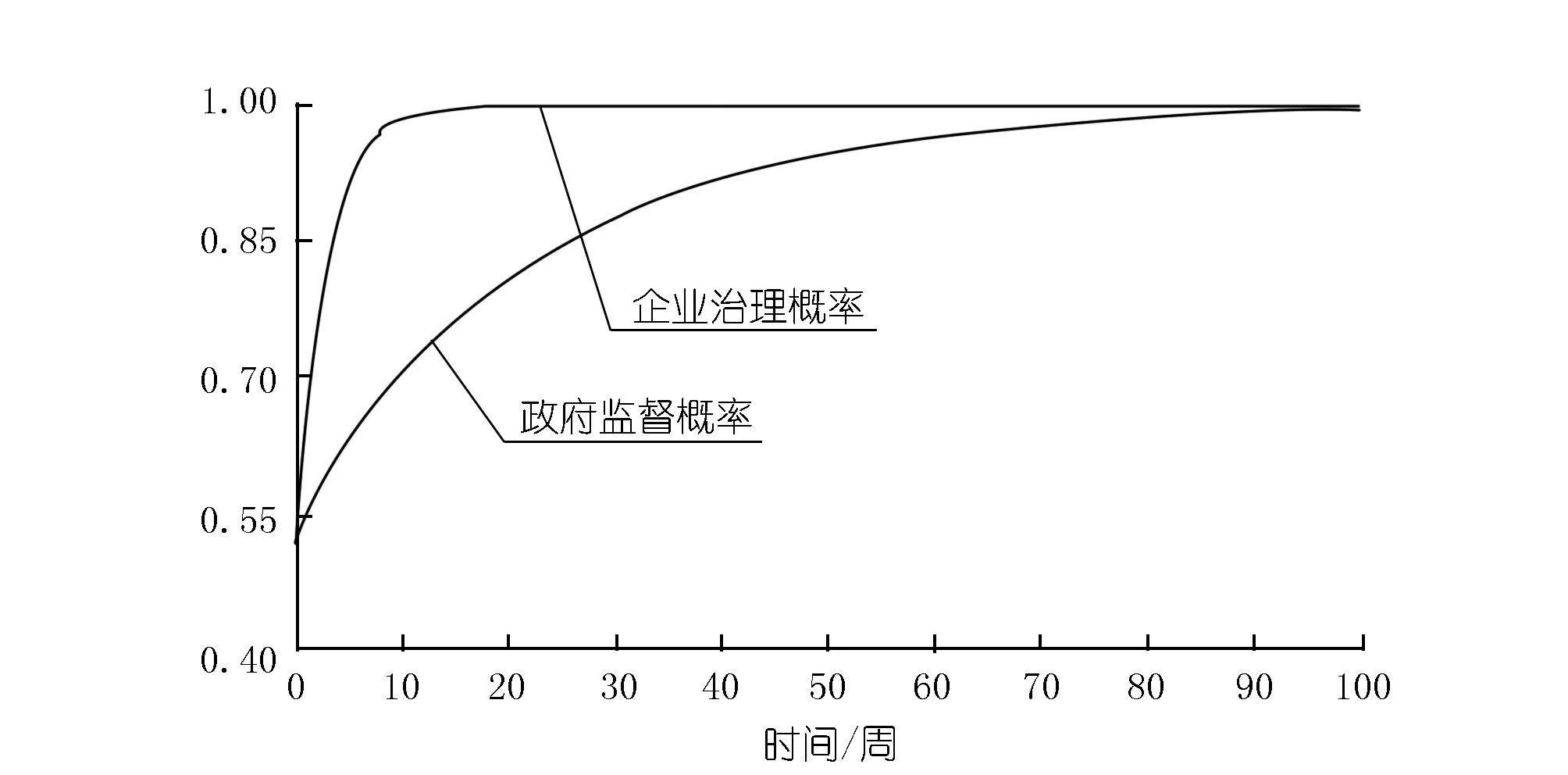
图5 地方政府与当地企业行为博弈仿真Fig.5 Game simulation of the behavior of local government and local enterprises

4 结论与建议

基于以上模型与实证研究结果可以看出：在中央政府与地方政府的博弈中，中央政府补贴与罚款、地方政府监督成本以及收益都会直接影响到双方的行为选择；地方政府与当地企业博弈时，地方政府的监督成本、企业治理成本等因素对双方行为的选择起着正向激励或者负向激励的作用。以重庆市万州区水资源生态补偿案例为例开展了实证分析，结果表明，仿真结果与实际案例中各方选择的行为相一致。

根据本研究的博弈与实证分析中影响水资源生态补偿最优策略解的变量，提出了以下政策性建议：

(1) 要因地制宜地实施监管模式，制定合理的奖惩机制。中央政府在制定政策时，应充分考虑到地方的区域发展与水资源开发的具体状况，可以征收并逐步提高水资源生态环境补偿税(费)。

(2) 完善地方政府水资源考核制度，鼓励地方政府主动执行水资源保护政策；将水中污染物增加量、三废污染物减少量以及公众对于水资源环境的满意度等纳入到考核指标的经济发展权重系数中。