漂浮式风力机在纵摇运动下的气动性能数值研究

方 圆，段 磊1,

(1.上海交通大学 海洋工程国家重点实验室，上海 200240；2.上海交通大学 船舶海洋与建筑工程学院，上海 200240)

0 引 言

漂浮式风力机的气动性能与其发电能力密切相关。但是，与固定式风力机不同，漂浮式风力机的气动性能受六自由度平台运动的影响，包括纵荡、横荡、垂荡、横摇、纵摇和首摇。其中，纵摇运动尤为重要且特殊：1）改变流体与叶轮之间的相对速度，从而直接影响推力、扭矩及功率[1]；2）导致叶轮处于不同的俯仰状态，对其气动性能也有影响[2]；3）使叶轮持续进出其尾涡场，进而间接影响其气动性能[3]。因此，本文拟对漂浮式风力机在平台纵摇运动下的气动性能展开研究。

截至目前，已有学者使用不同数值方法就相关内容展开研究，包括叶素-动量理论、动态尾迹模型和自由涡方法等。Jonkman 等[4]开发基于叶素-动量理论及动态尾迹模型的全耦合数值模拟工具FAST。Tran 等[5]使用上述2 种理论研究漂浮式风力机在纵摇运动下的气动响应。Shen 等和Wen 等[6-7]分别用自由涡方法研究风力机在纵摇运动下的非定常气动特性。然而，这些方法在本领域均有缺陷：叶素-动量理论结合不同动态入流模型使用经验公式及修正系数，无法准确预报瞬态剧烈变化的气动响应；动态尾迹模型基于诱导速度远小于风速假设，限制其在低风速下的应用；自由涡方法基于势流理论，无法准确模拟叶轮附近剧烈变化的流动现象。因此，需要更准确的数值方法对本文所述问题进行研究。

随着计算机的发展，计算流体力学（CFD）方法越来越多地被应用于复杂流体力学问题的模拟。其中，由于适中的计算量和精度，RANS（Reynolds averaged Navier-Stokes）模型被广泛运用。Tran 等[5]使用RANS模型研究漂浮式风力机在纵摇运动下的气动响应。Liu 等[8]使用RANS 模型研究漂浮式风力机在纵荡、垂荡及纵摇耦合运动下的气动特性。然而，RANS 模型时均化抹去重要涡结构，因此无法较好地模拟强非定常流动现象。相反，LES（large eddy simulation）模型虽然能对大尺度涡结构进行直接模拟，但是庞大的计算量制约其在工程上的应用。为兼顾计算效率和精度，本文采用由RANS 模型和LES 模型混合发展而来的IDDES（improved delayed detached eddy simulation）模型，其在近壁面使用RANS 模型，在远场使用LES 模型，兼具RANS 模型计算量低和LES 模型计算精度高的优点。截至目前，IDDES 已经被成功应用于垂直轴风力机[9]，但尚未被应用于本文所述问题的研究。

本文拟基于计算流体力学方法，使用IDDES 模型及重叠网格技术，对漂浮式风力机的气动响应和周围流场进行数值模拟，研究其气动性能在纵摇运动影响下的特性。

1 IDDES 湍流模型

IDDES 是结合了RANS 和LES 模型的混合模型，其湍动能方程为：

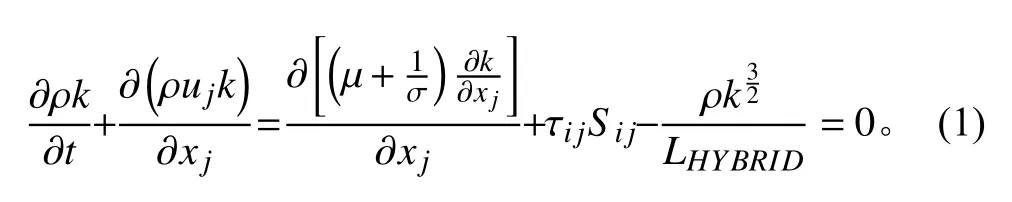
式中：k 为湍动能；τij为应力张量；Sij为平均应变率；uj及xj分别为速度及位移分量。LHYBRID为IDDES 长度尺度：

其中：

式中：γ为常数0.09；CDES为模型常数；ω为比耗散率；fB与 fe用于判断使用DDES（delayed detached eddy simulation）或WMLES（wall-modeled LES）模型进行计算，当来流有湍流成分时，激活WMLES 对边界层进行计算。此外，fdt与ΔIDDES分别为：

式中：rdt为壁面区域标记；Δmin为该网格中心到相邻网格中心的最小距离；Δ为网格尺寸；d为距壁面长度。

2 计算模型与网格

本文使用基于有限体积原理的STAR-CCM+软件实施数值模拟。

2.1 几何模型

研究对象选用Zhao 等[10]设计的1∶50 模型风力机。该模型风力机以美国国家可再生能源实验室5 MW 参考风力机为原型，基于傅汝德数相似定律，根据推力相似使用NACA4412 翼型重新设计而来，其几何模型如图1 所示。

图1 模型风力机三维模型Fig.1 The scale wind turbine model

2.2 计算域与网格

图2 计算域及边界条件Fig.2 The computational field and boundary setting

所有计算域形状均为圆柱体，以适应风力机旋转特点，如图2 所示。最外层计算域的长度和直径分别为9 倍和6 倍叶轮直径，入流段和出流段分别为3 倍和6 倍叶轮直径，其边界条件设置为速度入口和压力出口，四周为对称平面以避免边界影响。内层计算域包含2 层加密域，即网格尺寸从最外层计算域到最内层加密域以1∶2 进行2 次过渡，最内层加密域网格的基础尺寸为0.05 m。最内层加密域到旋转域的界面即为重叠网格界面，其两边网格尺寸保持一致，以保证计算精度。为避免叶轮发生较大变形，对叶片表面、轮毂和叶片随边进行面加密，如图3 所示。边界层网格的第1 层厚度为3.030 5×10-4m，增长率取1.2，以此确保叶片壁面的Y+值小于5，以符合软件规定。

图3 叶轮附近网格Fig.3 The mesh around the scale rotor

2.3 网格与时间无关性验证

为保证数值模拟的可靠性，本节使用叶轮推力为参数进行网格和时间无关性验证。

在边界层网格不变的前提下，将其他网格的基本尺寸增大或减小21/3（对应网格体积增大或减小2 倍），形成3 种网格划分，分别为粗糙网格、中等网格及精细网格。使用3 种网格，在风速1.61 m/s、转速85.41 r/min（尖速比7）的工况下进行数值模拟并与实验值[10]进行比对，如表1 所示。可知，粗糙网格计算结果的相对误差较大，精细网格的网格数量较大。综合考虑计算精度和效率，选取中等网格进行本文相关的所有数值模拟。

表1 不同网格精度对比Tab.1 Precision comprison of different mesh

选取3 个时间步长Δt1，Δt2和Δt3（对 应 每时间步叶轮旋转1°，2°和4°），在风速1.61 m/s、转速85.41 r/min、纵摇运动振幅2.25°、周期0.7 s 的工况下进行数值模拟并相互比对。如图4 所示，不同时间步长下的推力十分接近，仅在峰值处存在差别。其中，Δt2的推力曲线处于Δt1和Δt3的曲线之间。同样，综合考虑计算精度和效率，选取Δt2进行本文相关的所有数值模拟。

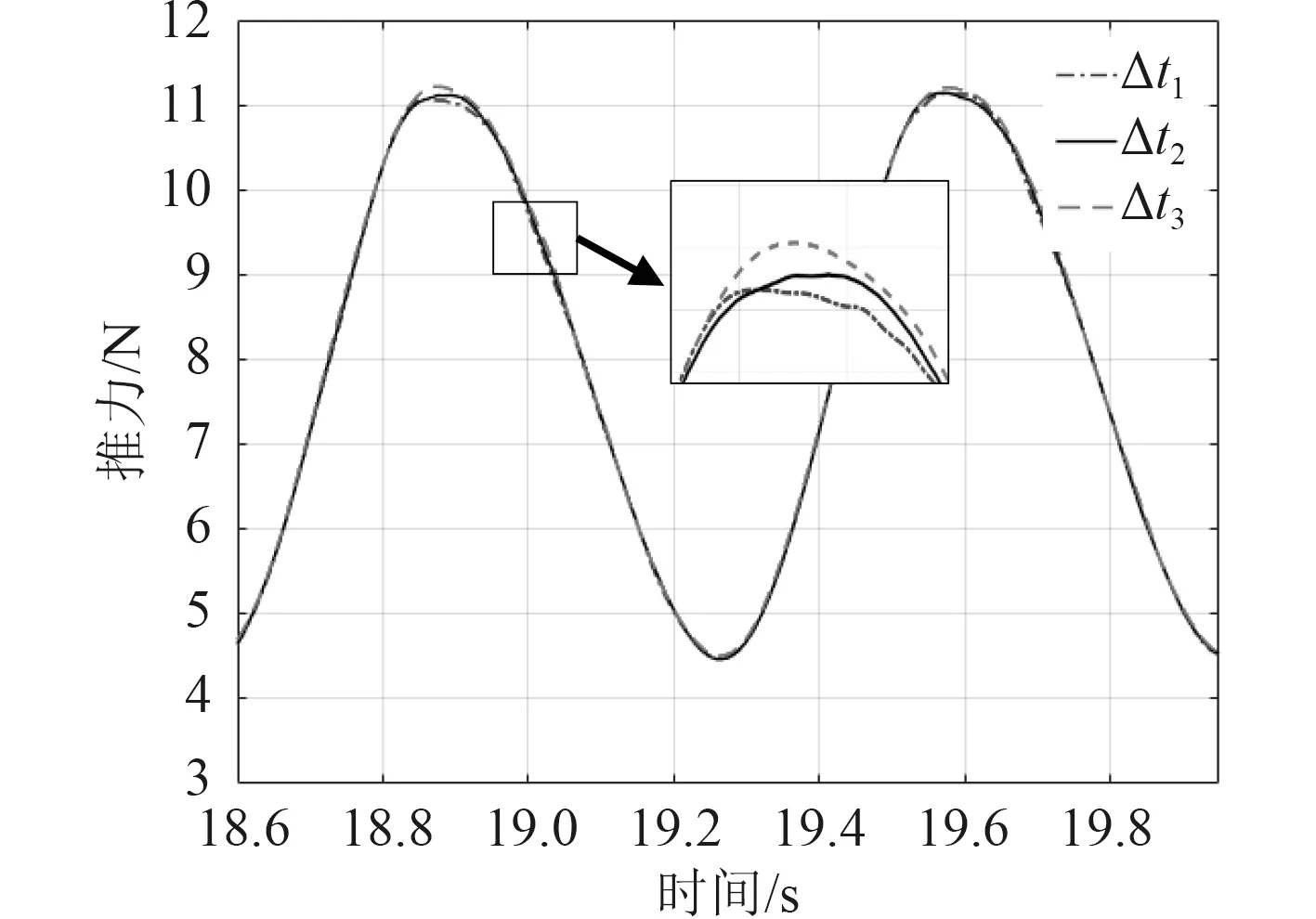
图4 不同时间步长下推力对比Fig.4 Comparison of the thrust at different time steps

2.4 风力机及平台纵摇运动参数设置

本文相关的所有数值模拟均在风速1.61 m/s、转速85.41 r/min（尖速比7）的工况下实施。平台纵摇运动中心为无运动下轮毂中心垂直向下1.54 m，运动形式为简谐运动，其位移和速度分别为：

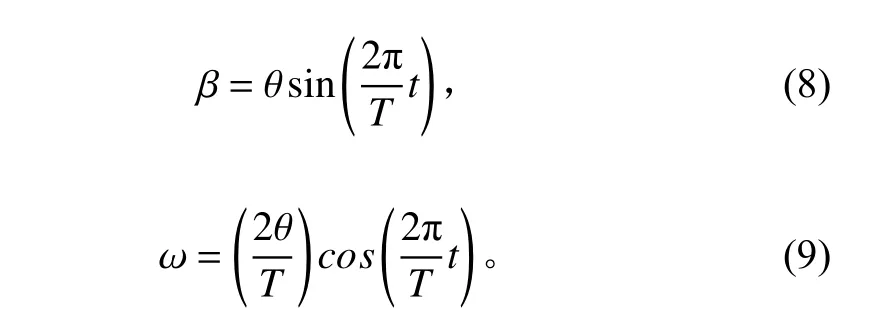
式中：θ为纵摇运动振幅，取1.5°，2.25°和3°；T为纵摇运动周期，取0.35 s，0.7 s 和1.4 s；t为时间。

3 数值模型验证

基于实验数据[10]对数值模型进行验证。其中，数值计算与实验中的模型风力机几何尺寸相同，风速、转速也相同。为节省计算时间，采用移动参考系法计算叶轮推力，并与实验值比对，如表2 所示。可知，相对误差绝对值均小于6%，最小相对误差绝对值0.51%出现在尖速比7 的工况下，即本文所有数值模拟所使用的工况，因此该数值模型可靠。

4 数值结果及分析

4.1 纵摇运动振幅对气动性能的影响

图5 为在相同纵摇周期（T=0.7 s），不同纵摇振幅下的叶轮推力、扭矩时域曲线。由图可知，存在以下现象：1）推力及扭矩曲线的平衡位置不受纵摇运动振幅的影响；2）推力及扭矩辐值随纵摇运动振幅增加而增大；3）推力和扭矩曲线关于其平衡位置不对称，以扭矩曲线较为明显；4）在推力和扭矩曲线峰值附近发生波动。

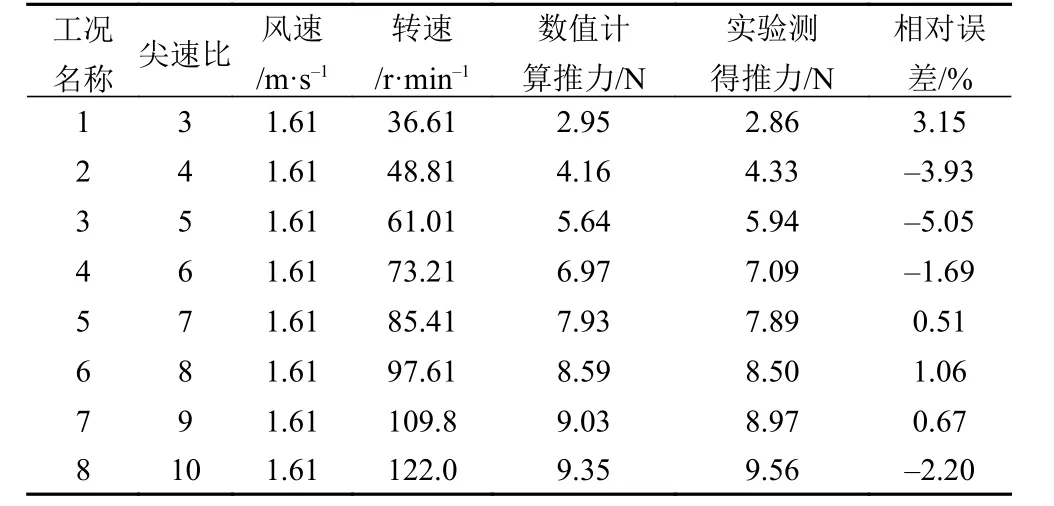
表2 数值模型验证工况及结果Tab.2 Validation of the numerical model at different TSRs

图5 不同纵摇运动振幅下的气动响应Fig.5 The aerodynamic performance with different pitch amplitudes

上述现象可借由叶轮与风之间的相对速度解释。漂浮式风力机在纵摇运动中，推力和扭矩与相对风速的平方成正比，相对风速由叶轮速度和自由风速合成，其中叶轮速度的幅值随纵摇运动振幅增加而增大，因此推力和扭矩的幅值随纵摇运动振幅增加而增大。且推力和扭矩的平衡位置大于零，上述平方关系将导致推力和扭矩曲线关于其平衡位置不对称。

叶轮与风之间相对速度的增加可能引起失速现象，进而使推力、扭矩曲线在峰值附近发生波动。为观察该现象，本文在典型纵摇运动（θ=3°，T=0.7 s）中，监测距轮毂中心0.7 倍叶轮半径处的叶片截面速度云图，如图6 所示。其中，图6（a）～图6（d）对应图6（e）中的T1～T4点。因为设置的纵摇运动速度正方向与自由风速正方向相反，所以纵摇运动速度变化趋势与相对速度变化趋势一致，即图6（a）对应的相对速度最大，并开始减小，至图6（c）对应的相对速度最小，再开始增大。图6（a）中叶片截面导边和随边均出现流动分离，即发生动态失速现象，引发升力降低、阻力增加，从而可以解释图5 推力及扭矩曲线出现在峰值附近的波动。

图6 典型工况下（θ=3°，T=0.7 s），距轮毂中心0.7 倍半径处叶片截面速度云图Fig.6 Velocity magnitude of one blade section at 0.7 radius from the hub center in a typical case (θ=3°，T=0.7 s)

4.2 纵摇运动周期对气动性能的影响

图7 为在同一纵摇振幅（θ=2.25°），不同纵摇周期下的叶轮推力、扭矩时域曲线。存在以下现象：1）推力及扭矩曲线的平衡位置不受纵摇运动周期的影响；2）推力及扭矩辐值随纵摇周期减少而增大；3）推力和扭矩曲线关于其平衡位置不对称，以扭矩曲线较为明显。

上述现象也可借由相对速度解释。如4.1 节所述，推力和扭矩与相对风速的平方成正比，相对风速由叶轮速度和自由风速合成，其中叶轮速度的幅值随纵摇运动周期减少而增大，因此推力和扭矩的幅值随纵摇运动周期减少而增大。且推力和扭矩的平衡位置大于零，上述平方关系将导致推力和扭矩曲线关于其平衡位置不对称。

图7 不同纵摇运动周期下的气动响应Fig.7 The aerodynamic performance with different pitch periods

图8 典型工况下（θ=3°，T=0.35 s），漂浮式风力机气动响应时域变化Fig.8 The aerodynamic performance in a typical case (θ=3°，T=0.35 s)

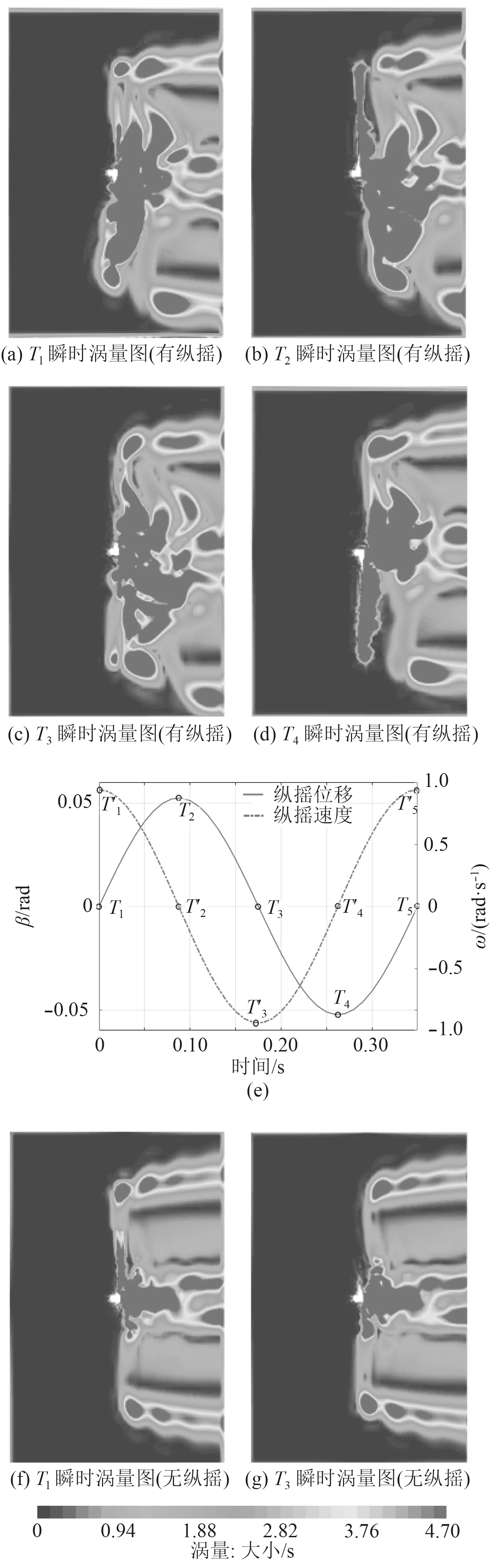
图9 典型工况下（θ=3°，T=0.35 s），一个纵摇周期内尾涡瞬时变化Fig.9 The instantaneous vorticity within one pitch period in a typical case (θ=3°，T=0.35 s)

此外，叶轮进出尾涡场可能引起尾涡干扰现象。为观察该现象，本文提取典型纵摇运动（θ=3°，T=0.35 s）中推力和扭矩的时域曲线，如图8 所示。其中，图8（a）和图8（b）中推力和扭矩曲线由上向下穿越平衡位置时发生曲率变化，图8（b）中扭矩曲线在谷值附近发生明显波动。该现象可以由图9 监测的尾涡解释。图9（a）～图9（d）对应图9（e）中的T1～T4点。同样，因为设置的纵摇运动速度正方向与自由风速正方向相反，所以纵摇运动速度变化趋势与相对速度变化趋势一致，即图9（a）对应叶轮处于平衡位置，迎风运动速度最大，叶尖涡间距与固定式风力机相近（对比图9（f））；图9（b）对应叶轮处于最远离尾涡场位置，运动速度为0，即将开始顺风运动，叶尖涡间距最大；图9（c）对应叶轮处于平衡位置，顺风运动速度最大，叶尖涡间距与固定式风机相近（对比图9（g））；图9（d）对应叶轮处于最深入尾涡场位置，运动速度为零，即将开始迎风运动，叶尖涡间距最小。上述推力、扭矩曲线在平衡位置附近的曲率变化对应图9（e）中T2点附近，即叶轮处于最远离尾涡场位置，运动速度为0，即将开始顺风运动，同时拍击尾涡。而扭矩曲线在谷值附近的波动对应图9（e）的T3点附近，即叶轮处于平衡位置，顺风运动速度最大，同时拍击尾涡最剧烈。从能量角度分析，叶轮拍击尾涡，尾涡场将部分能量传递给叶轮，使其推力及扭矩略增大，从而可以解释图8 推力及扭矩曲线出现在平衡位置附近的曲率变化以及扭矩曲线出现在谷值附近的波动。

4.3 纵摇运动对叶轮平均功率的影响

图10 为在各种工况下的叶轮平均功率。存在以下规律：1）纵摇运动下的叶轮平均功率大于无平台运动时的叶轮平均功率；2）相同纵摇振幅下，叶轮平均功率随着纵摇周期的增加而减小；3）相同纵摇周期下，叶轮平均功率随着纵摇振幅的增加而增大。上述规律也可借由相对速度解释，同4.1 和4.2 节。

图10 叶轮平均功率在各种纵摇运动和无运动工况下的对比Fig.10 Comparison of averaged rotor power with and without pitch motion

5 结 语

本文在STAR-CCM+软件中使用IDDES 模型，对模型漂浮式风力机在纵摇运动下的气动响应和周围流场实施数值模拟。研究结果表明，漂浮式风力机气动性能受纵摇运动影响较大，应在设计阶段予以考虑，具体如下：

1）叶轮推力和扭矩的辐值随纵摇运动振幅增加而增大。叶轮迎风运动导致相对速度增加，可能发生动态失速现象，期间升力减小、阻力增大，对风力机产生不利影响。

2）叶轮推力和扭矩的辐值随纵摇运动周期增加而减小。叶轮顺风运动导致叶轮进入尾涡场，可能发生尾涡干扰现象，期间尾涡将部分能量传递给叶轮，对风力机产生部分有利影响。

3）叶轮平均功率在纵摇运动下有所提高，随纵摇运动振幅增加而增大，随纵摇运动周期增加而减小。