基于FNN-GARCH组合模型的船舶电磁仪表器材消耗预测研究

吴雯雯

[摘    要] 针对船舶电磁仪表器材消耗预测过程中存在的数据序列波动性问题，结合电磁仪表器材消耗特点和维修保障工作实际，分别建立了模糊神经网络模型（FNN）和广义自回归条件异方差模型（GARCH）以及FNN-GARCH组合模型，通过比较研究，基于FNN-GARCH1组合模型来对电磁仪表器材消耗量进行预测，可以很好地提高预测精度，为电磁仪表器材维修保障决策提供了定量依据和实用预测方法。

[关键词] FNN模型;GARCH模型;FNN-GARCH组合模型;消耗预测;船舶电磁仪表;器材

doi ： 10 . 3969 / j . issn . 1673 - 0194 . 2020. 15. 056

[中图分类号] F224    [文献标识码]  A      [文章编号]  1673 - 0194（2020）15- 0130- 02

0      前    言

在船舶设备器材中，电磁仪表器材占有很大的比重。随着时间的推移，电磁仪表会因储存寿命周期、仪表故障率、使用人员操作技能、使用强度、任务变化、装备更替、管理水平以及海上水文气象条件等因素的影响，出现电磁仪表器材消耗的情况。由于旧的或者需要维修的电磁仪表器材在被更换或维修之后，会出现新旧仪表与维修后的仪表同时工作的情况，因此，电磁仪表器材的消耗规律十分复杂，而其消耗规律又会直接影响维修保障过程中电磁仪表器材备品备件的库存决策。可见，寻求一种能够有效预测电磁仪表器材消耗量的方法是十分必要的。

1      样本数据获取

为了研究船舶电磁仪表器材的消耗规律，这里选取了2017年至2019年某船舶电磁仪表器材消耗的实际数据，如表1所示。

2      组合模型的建模步骤

（1）依据电磁类消耗量时间序列建立ARMA模型，以消除数据线性部分的影响。（2）检验残差的异方差性。如果消耗量序列具有无异方差性，则选择ARMA模型;如果有异方差性，则建立异方差模型。（3）验证序列的ARCH效应。如果具有ARCH效应，

则建立GARCH模型，消除不显著的变量。（4）修正或改进GARCH模型，如果模型能够实现对电磁类仪表器材消耗量的准确预测，则选择GARCH模型。（5）选择模糊神经网络模型FNN与GARCH模型组合，建立组合预测模型[1]。

3      ARMA模型的建立

3.1   消耗量数据序列的ADF检验

设定检验的显著性水平为α=0.05，则消耗量数据序列{xt}的单位根ADF检验结果，如表2所示。

在进行单位根检验时，假定原来的假设为：H0：消耗量数据序列中存在一个单位根，由于Prob.为：0.138 7>0.05，因此，接受原来的假设，即消耗量数据序列是不平稳的。进行一阶差分处理后，对新序列进行单位根检验，结果如表3所示。

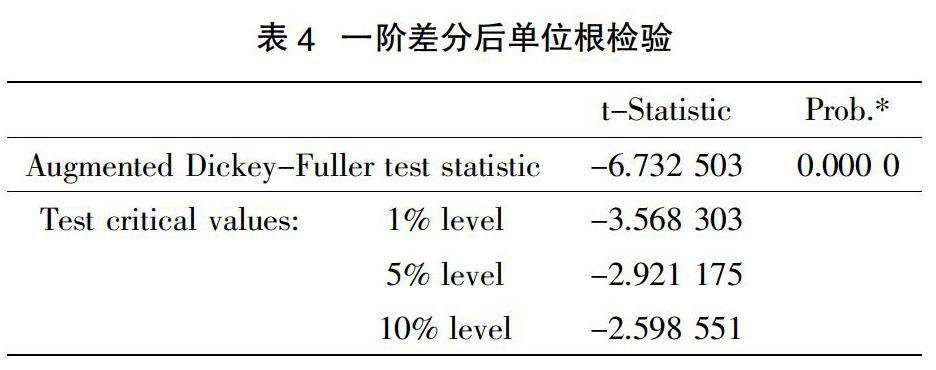
由表3可知，Prob.=0.000 1<0.05，因此，可以拒绝原来的假设，即一阶差分后的消耗量数据序列是平稳的[2]。将一阶差分后的数据序列再进行单位根检验，结果如表4所示。

3.2   消耗量序列的峰度与偏度

消耗量序列峰度与偏度检验结果为：Mean：26.992 57;Median：22.053 81;Maximum：94.511 42;Minimum：1.454 689;Std.Dev：21.248 29;Skewness：1.246 123;Kurtosis：4.030 381;Jarque-bera：18.182 44;Probability：0.000 113。由此可见，峰度大于3，偏度大于0，这表明该序列具有明显的尖峰性，与正态分布相比是右偏的。Jarque-bera值为：18.18 244>0，Prob.=0.000 113，说明消耗量序列不服从正态分布，具有明显的非线性特征。

3.3   消耗量的ARMA预测模型

对消耗量序列残差进行白噪声检验可知，每一阶的滞后项p>0.05，自相关和偏相关值基本在边界线以内，说明可以建立ARMA模型进行预测。由于是序列基本平稳的，因此，可得模型：Y=0.272 48×Y（-1）+0.491 73×Y（-2）+0.804 36

4     GARCH模型的建立

GARCH模型运用过去的方差及其预测值来构建未来方差的自回归条件异方差时间序列模型。GARCH效应，一是指异方差性，即随着时间的变化方差也会相应地發生变化;二是条件性，即预测值与过去的相邻观测值有关，相邻观测值的个数会随着阶数的增加而同步增加。

4.1   异方差性与ARCH效应检验

设随机干扰项εt～ARCH（q），则ht=α0+α1εt-1+…+αt-q。为检验该序列是否存在ARCH效应，可做原假设：H0：α1=α2=…=αq=0，H1：？埚αi≠0（1≤i≤q）。对残差序列进行ARCH效应检验：Prob.F（1，57）：0.0095;Prob.Chi-Square（1）：0.0101。由此可见，P值均小于0.05，因此，残差序列是相关的且具有异方差性，存在ARCH效应，可以运用GARCH类模型进行建模预测。

4.2    GARCH模型

GARCH模型是在自回归条件异方差模型ARCH基础上发展而来的，ARCH模型比较适用于短期自相关系数的问题，对于长期的自相关问题则需要通过增加移动平均阶数来对模型进行改进，构建GARCH模型，以提升对器材消耗量的预测精度。

5      组合模型的建立

5.1   组合模型的建模步骤

组合模型的建立步骤：一是建立电磁类仪表器材消耗量数据序列{xt，t=1，2，…，n}时间序列模型xt的线性部分;二是建立GARCH模型对随机干扰项进行预测，对非线性部分运用FNN模型建模预测。

将60个数据中的48个数据作为训练样本，其余的12个数据作为测试样本。为了提升预测精度，对原始数据序列做以下变换：

Yt=log（Xt），t=1，2，…，60。

5.2   组合模型的建立过程

建立两种混合模型FNN-1和FNN-2，其中：FNN-GARCH1模型：■t=f（■t，■t）

FNN-GARCH2模型：■t=f（■t）

其中，■t为GARCH模型的预测值，■t为异方差预测值。

5.3   变换后残差序列的ARCH效应检验

变换后残差序列的ARCH效应检验结果为：Prob.F（2，57）：0.000 0;Prob.Chi-Square（2）：0.000 0。由此可知，残差序列存在ARCH效应。可以对消耗量数据序列滞后模型的残差项建立GARCH（1，1）模型并对参数进行估计，估计结果如表5所示。

由此可得出模型：Yt=3.140 256Yt-1+εt

GARCH=0.003 01-0.174 27×RESID（-1）2+1.064 61×GARCH（-1）

6      模型比较分析

采用2017年至2019年的电磁仪表器材消耗数据进行拟合，求出各种模型的拟合结果并分别计算出各个模型的平均绝对误差（MAE）值、平均绝对百分比误差值（MAPE）以及均方百分比误差（RMSE）值，如表6所示。通过比较各个误差值的大小，选出三个误差值都最小的，作为电磁仪表器材消耗量估计的最优预测模型。

从表6中可知，FNN-GARCH1组合模型的MAE、MAPE、RMSE的值与其他模型相比都是最小的，因此，FNN-GARCH1组合模型能够较为准确地预测船舶装备电磁类仪表器材消耗量情况。

7      结    论

电磁仪表器材是保障机电设备正常工作的关键部件之一，做好船舶电磁仪表器材消耗的预测工作是维修保障决策的重要环节。将FNN模型与GARCH模型相结合，建立FNN-GARCH1组合模型，可以克服采用单一方法预测的缺陷，提升电磁仪表器材消耗预测的准确性和可靠性，其预测值可以作为维修保障决策的定量依据。

主要参考文献

[1]马艳青.马尔科夫转换-GARCH模型的MCMC参数估计和方法研究[D].重庆：重庆大学，2015.

[2]李玉芳.波动率分析：GARCH族及模糊时间序列模型[D].杭州：浙江大學，2012.