基于CZM模型的锚杆拉拔脱粘特性研究

卢 杰，李敏敏

(河南理工大学 土木工程学院，河南 焦作 454000)

随着我国基础设施的大规模建设，特别是能源、水利、交通和城市基础设施建设的增加，必须面对大量的岩石开挖及处理的问题。因此，研究锚固问题具有重要意义。对锚杆拉拔脱粘这一课题进行深入研究，以此来提高传统锚杆锚固力，有利于我国锚杆支护的深入发展。

粘结式锚杆是目前锚杆支护技术中常用的一种支护方式，这种支护方式可有效加固围岩和改善围岩强度。国内学者对锚杆支护的初步探索始于1956年，由于当时的科学技术条件限制，直到1990年以后才开始迅速发展。谭鑫等[1]基于收敛约束法原理，推导了考虑锚杆与围岩共同作用的圆形隧道围岩特性曲线弹性响应函数。赵呈星等[2]通过建立预应力锚杆围岩模型，得到在不考虑滑移的条件下，当自由段轴力为定值时，锚固段轴力沿锚杆长度逐渐减小至零。近年来，随着地下巷道的发展，锚杆支护的研究也越来越多[3-6]，但是这些研究多数只是对试验结果的总结，深刻且全面的理论分析却相对较少。本文借助有限元软件，对全长粘结式锚杆脱粘特性进行了研究，重点分析了锚杆的破坏模式和锚固机理。

1 CZM模型的建立

1.1 基本理论

1.1.1 粘结滑移应力分析

CZM(cohesive zone model)即粘结区域模型，在两个界面中插入一个粘结区域，来研究粘结区域的破坏。Benmokranet等[7]对于锚杆脱粘做了相关试验，用来研究理想化粘结滑移关系。锚杆由七股钢绞钢丝线组成，直径Φ=15.8 mm。所以选择4Φ长度的粘膜是因为粘结的长度比较短时，可近似假定粘结应力在破坏附近沿灌浆-锚索界面均匀分布。经过用不同的水泥浆以及多次试验之后得出结论：粘膜破坏分为3个阶段：弹性阶段、脱粘破坏阶段、粘膜完全破坏阶段。

剪应力和滑移之间的函数表达式：

τ=ms+n

(1)

当0≤s≤s1时

(2)

当s1≤s≤s2时，

(3)

当s2≤s时，

m=0；n=τ2

(4)

式中：τ为锚杆和水泥浆之间的粘膜所受切应力；s为锚杆和水泥浆之间的滑移；m，n为系数。

损伤变量D和位移s的关系为：

(1-D)K=τ/s

(5)

式中：τ为剪应力；D为损伤模量；K为剪应力-滑移曲线上的点与原点所成直线的斜率。

1.1.2 粘膜受力的理论分析

轴向张拉荷载施加于锚杆的端部，通过对锚杆某一单元进行受力分析，如图1所示。

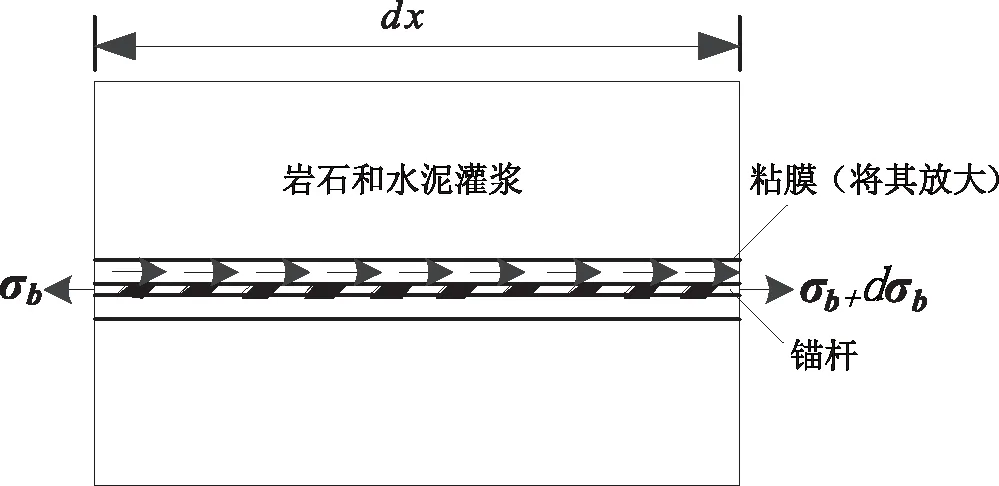
图1 锚杆上一个单元的受力图

建立锚杆轴向应力与交界面剪应力的关系式

Adσb=-τbπdbdx

(6)

(7)

式中：A为锚杆横截面积；db为锚杆直径。

由于面积是常数，则可知面积与应力微分的乘积为轴力的微分，即剪力与dFN/dx成正比。也即轴力的斜率与一个常数的乘积即为粘膜的剪力。

1.2 锚杆脱粘的建立

假设锚杆、岩石粘膜是均匀的，选择圆柱状岩石为研究对象以形成CZM模型。在模型里一共用到4种材料：锚杆、粘膜、水泥灌浆、岩石。锚杆是用钢绞线所制，其弹性模量是210 GPa，泊松比是0.28，直径是15.8 mm；粘膜实际上是水泥灌浆与锚杆接触处形成的，水泥灌浆28 d固化后其抗压强为52.6 MPa，抗拉强度为3.8 MPa，弹性模量为35 MPa，泊松比为0.14；岩石抗压强度为60 MPa，弹性模量为30 MPa，泊松比为0.14。采用轴对称模型。

2 计算结果及分析

2.1 固定锚固长度时锚杆和粘膜的受力分析

2.1.1 固定锚固长度时锚杆受力分析

建立模型：设置锚杆长度为170 mm，同时设置混凝土圆柱长度为142 mm。对于所建立的模型，分别施加从小到大的位移边界条件，拉拔力与锚杆受拉端位移关系如图2所示。从图2可知，当锚杆受拉位移是3 mm，此时锚杆受拉端位移较小，随着锚杆受载端位移的增大，拉拔力也越来越大；当位移边界条件是9 mm，开始时随着位移逐渐变大，拉拔力逐渐变小，随后再继续增大时，拉拔力的数值逐渐趋于平稳。当锚杆受拉位移是15 mm时，与锚杆受拉位移为9 mm时相比，初始端的受力完全相同。为了验证模拟结果的正确性，现将模拟数据与Benmokrane的试验数据进行对比分析。

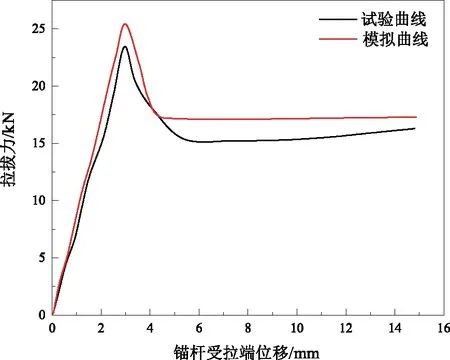
图2 试验数据与模拟数据的对比分析

通过对比可知，模拟的数值基本是正确的。可以得出如下结论：锚杆的脱粘分为3个阶段，第一阶段是弹性阶段，粘膜并未发生破坏，随着载荷的增加，受拉端的位移线性增加；第二阶段是粘膜破坏阶段，此时整个模型的受载能力下降，粘膜逐渐发生破坏；第三阶段是完全破坏阶段，此时锚杆只受到破坏后的粘膜对其的摩擦力，比较均匀。

2.1.2 固定锚固长度时粘膜受力分析

取锚固长度为1 000 mm，对锚杆受拉端位移不同时在粘膜破坏前后其剪力的变化进行分析，锚杆拉拔力与位移的关系，如图3所示。沿锚杆粘膜的剪力分布情况，如图4所示。从图3-图4可知，当锚杆受拉端位移是1 mm时，锚杆粘膜没有发生破坏，粘膜所受剪应力随锚固长度的增大而增大。

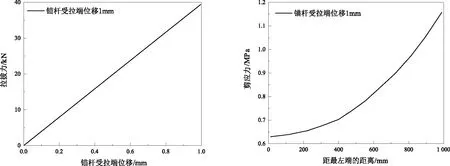
图3 拉拔力-位移的关系 图4 沿锚杆粘膜的剪力分布

2.2 锚杆脱粘与锚固长度的关系

为了对比分析不同锚固长度对锚杆脱粘的影响，现将锚固长度分别设定为锚杆直径的4倍、9倍、14倍和20倍，如图 5所示。由图5可知，在初始阶段，随着锚杆受拉端位移的增大，拉拔力也随之增大；锚固长度越大，最大抗拉拔力越大；锚固长度在一定范围内变化时，破坏时的拉伸位移的大小相近，增加锚固长度，并不能增大破坏时的位移，锚固长度不同，但破坏的机理相同。最大拉拔力与锚固长度的关系，如图6所示。锚固长度与最大拉拔力近似线性关系，即在一定范围内，锚杆脱粘粘结力和锚固长度的关系为[8]：

F=0.13L+5.66

(8)

式中：F为最大拉拔力，kN；L为锚杆锚固长度，mm。

图5 拉拔力-位移 图6 最大拉拔力-锚固长度

3 结 语

基于CZM模型的锚杆拉拔脱粘特性，分析脱粘过程以及不同过程中粘膜受到的剪应力，以及拉拔力与锚固长度的关系，得出以下结论：

(1)锚杆的脱粘分为3个阶段：第一阶段是弹性阶段，粘膜并未发生破坏，随着载荷的增加，受拉端的位移线性增加；第二阶段是粘膜破坏阶段，此时整个模型的受拉能力下降，粘膜逐渐发生破坏；第三个阶段是完全破坏阶段，此时锚杆只受到破坏后的粘膜对其的摩擦力。

(2)锚固长度在一定范围内变化时，破坏时的拉伸位移的大小相近，增加锚固长度，并不能增大破坏时的位移。锚固长度越大，抗拉拔力就越大。