环Z4+uZ4上负循环码的Hamming距离
2020-10-27王艳萍
王艳萍,李 杰
(宿州学院 数学与统计学院,安徽 宿州 234000)
随着对环Z4的研究,编码学者对环上循环码、常循环码进行了大量的研究[1-5]。其中,负循环码作为一类特殊的常循环码,也被广泛研究[6-8]。负循环码在整个编码与密码领域中有着重要的应用,其性质的探究显得格外重要。近些年,链环上码的研究相对成熟,非链环上码的研究相对较少。本文将研究一类非链环上码的一些性质,主要通过对环Z4+uZ4负循环码结构及性质的研究,定义了环上挠码和剩余码的概念,通过负循环码及其挠码的关系,讨论了该环上负循环码的Hamming距离,为编码与密码学提供了理论参考。
1 预备知识
记R=Z4+uZ4={a+ub|a,b∈Z4,u2=0},且R≅Z4[u]/
定义1 在Rn上,有τ-1(c0,c1,…,cn-1)=(-cn-1,c0,…,cn-2),对线性码C有τ-1(C)=C,则码C是R上的负循环码。
下记S=Z4,Rn=R[x]/(xn+1),Sn=S[x]/(xn+1)。∀f(x)∈Rn,能唯一写成f(x)=f1(x)+uf2(x),f1(x)、f2(x)∈Sn。如无特殊说明,本文所出现的R、S、Rn、Sn均为上述记法,且约定文中的n=2k。
引理1 在Rn中,假设m=2k,k∈N+,则有(x+1)m=xm+1+2xm/2。
引理2 在Rn中,若当n=2k,k∈N+时,则Rn为局部环,且其极大理想为(u,x+1)。
证明 可定义映射Φ:Rn→Sn,有Φ(f(x))=f1(x)mod(u),易证Φ为满同态。由文献[9]可知:Z4[x]/(x2k+1)是局部环,(x+1)为其极大理想。则有Φ-1((x+1))=(u,x+1)。又因(u,x+1)里包含Rn中的所有非单位,所以(u,x+1)是Rn唯一极大理想,即Rn是局部环。
引理3 在Rn中,(x+1)n=2xn/2,(x+1)为幂零元,幂零指数为2n。
证明 (x+1)n=xn+1+2xn/2,因xn=-1,(x+1)n=2xn/2,则(x+1)2n=0。下证,不∃l<2n,有(x+1)l=0。设∃n 引理4[10]记I为Rn上的理想。如果T是满足下面式子的最小正整数。 u(x+1)T∈I=((x+1)s+u(x+1)th(x)) 当1≤s≤n-1,0≤t 当n≤s≤2n-1,t 当n≤s≤2n-1,t≥s-n,degh(x)≤n-t-1,h(x)∈Sn为单位时,则T=min{s,2n-s+t}; u(x+1)T∈I=((x+1)s+2u(x+1)th(x)) 当n≤s≤2n-1,0≤t u(x+1)T∈I=((x+1)s+u(x+1)t(2h1(x)+(x+1)lh2(x))) 当n≤s≤2n-1,0≤t 注1 假设T1为使得当2u(x+1)T1∈I=((x+1)s+u(x+1)th(x))时对应的最小值,在此不再具体讨论。 为讨论环R上负循环码的Hamming距离,首先定义其挠码与剩余码。 由上述概念,可得: (1)平凡理想 ① 当C=(0)时,则有Tor(C)=Res(C)=(0); ② 当C=(1)时,则有Tor(C)=Res(C)=(1); (2)主理想 ① 当C=(u(x+1)m),0≤m≤2n-1时,则有Tor(C)=((x+1)m),Res(C)=(0); ③ 当C=((x+1)s+2u(x+1)th(x)),n≤s≤2n-1,0≤t ④ 当C=((x+1)s+u(x+1)t(2h1(x)+(x+1)lh2(x))),n≤s≤2n-1,0≤t (3)非主理想 ① 当C=((x+1)s+u(x+1)th(x),u(x+1)m),1≤s≤2n-1,0≤t ② 当C=((x+1)s+2u(x+1)th(x),u(x+1)m),n≤s≤2n-1,0≤t ③ 当C=((x+1)s+2u(x+1)th(x),2u(x+1)m1),n≤s≤2n-1,0≤t ④ 当C=((x+1)s+u(x+1)t(2h1(x)+(x+1)lh2(x)),u(x+1)m),n≤s≤2n-1,0≤t ⑤ 当C=((x+1)s+u(x+1)t(2h1(x)+(x+1)lh2(x)),2u(x+1)m1),n≤s≤2n-1,0≤t 引理5 对R上负循环码C(n=2k),有dH(C)=dH(Tor(C))。 证明 因为uTor(C)⊆C,所以有dH(C)≤dH(uTor(C))=dH(Tor(C))。又∀0≠c∈C,如果c(modu)=0,则∃0≠c′∈Tor(C),有c=uc′,所以WH(c)=WH(uc′)=WH(c′)≥dH(Tor(C))。如果c(modu)≠0,则c(modu)∈Res(C)⊆Tor(C),所以WH(c)≥WH(c(modu))≥dH(Tor(C))。即证。 命题1[11]Z4上长为n=2k的负循环码为码C,则C=((x+1)i),0≤i≤2n,其Hamming距离: 由引理5、命题1及上述挠码分析,可得本文重要定理。 定理1R上长为n的负循环码C,有C的Hamming距离: (1)当C=(u(x+1)m),0≤m≤2n-1时,dH(C)=Δm; (2)当C=((x+1)s+u(x+1)th(x)),1≤s≤2n-1,1≤t (3)当C=((x+1)s+2u(x+1)th(x)),n≤s≤2n-1,0≤t (4)当C=((x+1)s+u(x+1)t(2h1(x)+(x+1)lh2(x))),n≤s≤2n-1,0≤t 证明(1)因当C=(u(x+1)m)时,有Tor(C)=((x+1)m),又dH(C)=dH(Tor(C)),由命题1可知dH(C)=Δm; (2)当C=((x+1)s+u(x+1)th(x))时,有Tor(C)=((x+1)T)其中 将T的值代入命题1,可得 同理可证结论(3)和结论(4)。 注2 对于非主理想的情形,易得dH(C)=Δm与dH(C)=Δm1。 本文主要通过定义R上的挠码与剩余码,来讨论R上负循环码的Hamming距离,为代数编码与密码学提供了理论基础,后续将进一步研究该环上常循环码、对偶码等性质。2 环R上负循环码的Hamming距离
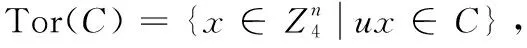
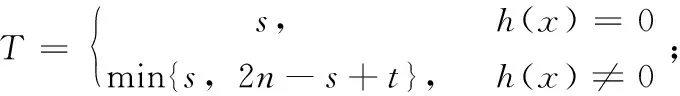
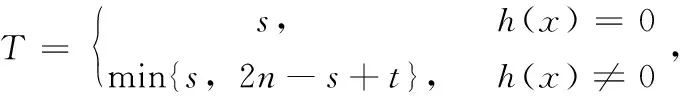
3 结 语
