一种抗眩晕训练平台三自由度并联机构优化设计
2020-10-27曹建平王海东高富东
曹建平,王海东,高富东
(海军航空大学青岛校区, 山东 青岛 266041)
抗眩晕训练是海军舰艇人员的必备训练科目,目前训练器材局限于滚轮、旋梯及浪木等手动式装置,这些装置仅能进行单方面的往复运动,无法模拟复杂海况下船舶多方向运动引起的机体眩晕感,因此设计一种能模拟船舶多自由度运动的训练平台非常必要。考虑到承载能力和运动精度,复杂海况下船舶运动模拟平台一般基于并联机构设计,包括六自由度[1]、三自由度[2]、二自由度[3]并联机构。人员晕船是由船舶的周期性振荡引起的,船舶的六自由度运动中,只有垂荡、横摇和纵摇运动是纯粹的振荡运动,因此三自由度并联机构更适用于抗眩晕训练。
灵巧度是衡量并联机构输入与输出运动之间传递精度和评价机构运动学性能的重要指标[4],众多学者以灵巧度为指标对并联机构进行了优化设计。针对单一指标评定灵巧度的局限性,陈修龙等[5]定义了一种能综合评价不同位形下并联机构灵巧度的指标——平方平均灵巧度系数。于凌涛等[6]提出了全域空间条件数均值与全域空间条件数波动值的综合灵巧度指标。作为优化问题评价指标时,灵巧度必须考虑全域范围的值,在定义全域值时一般都是基于工作空间计算,而三自由度并联机构可达工作空间较小,因此还应考虑可达工作空间每个位置所有姿态下的复合灵巧度,这样的评价对优化设计更具有指导意义。
在优化设计算法方面,马致远等[7]采用差分进化算法对一种三平移并联机构进行多目标优化,鲁凯等[8]采用遗传算法对8-SPU并联机器人进行优化,Cahill等[9]对二自由度并联机构提出了一种几何代数方法。Wang 等[10]利用多目标粒子群(MOPSO)算法对平面三自由度并联机构进行优化。人工蜂群算法(artificial bee colony,ABC)是Karaboga等[11]于2005年提出来的一种群智能全局优化算法,可应用于多种工程优化问题,但目前在并联机构的优化设计方面应用不多。
本文设计了一种新的用于抗眩晕训练的2UPS-PU并联机构,给出位置反解和运动速度雅克比矩阵,证明了该机构的线速度条件数恒为1,为衡量角速度的灵巧度,提出了离散型全姿态空间条件数指标,并以此指标为目标函数,采用人工蜂群算法对2UPS-PU并联机构结构参数进行了优化。
1 2UPS-PU并联机构
1.1 机构描述
如图1所示,并联机构包括动平台B1B2B3和固定平台A1A2A3,动平台B1B2B3通过2个结构完全相同的无约束主动支链AiBi(i=1,2)和1个恰约束主动支链A3B3与固定平台A1A2A3连接。动平台B1B2B3和固定平台A1A2A3分别呈等腰直角三角形。恰约束主动支链A3B3一端通过万向铰B3与动平台B1B2B3相连接,另一端与固定平台A1A2A3固定连接,用来限制动平台的摇艏、横荡和纵荡运动。无约束主动支链A1B1和A2B2一端通过万向铰B1和B2与运动平台B1B2B3相连,另一端通过球铰A1和A2与固定平台A1A2A3相连,当移动副L1,L2和L3伸缩时可以使动平台实现既定的横摇、纵摇和垂荡运动。

图1 2UPS-PU并联机构结构简图
1.2 位置反解
当已知机构动平台的位置和姿态时,求解机构主动件的位置称为位置反解。建立如图1所示的坐标系,设R:OXYZ为固定在固定平台上的基础坐标系,R′:oxyz为固定在动平台上的动坐标系,动平台A1A2A3和固定平台B1B2B3边长分别为r和R。Ai(i=1,2,3)为点Ai的位矢,Bi(i=1,2,3)为点Bi的位矢,φ为矢量A3B3与固定平台的夹角,θ为矢量A3B3在固定平台的投影与矢量A1A2的夹角。下文约定c、s、ct分别表示cos、sin和ctan。
运动坐标系原点B3(o)在基础坐标系下表示为:
(1)
式中:z为位矢B3相对于固定平台B1B2B3的垂线高度。
位矢Ai在基础坐标系下表示为:
(2)
位矢Bi在动坐标系下表示为:
(3)
则位矢Bi在基础坐标系下表示为:
(4)
其中:
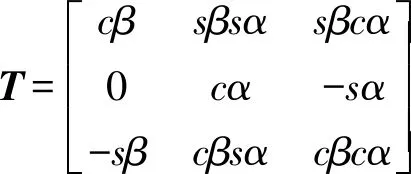
式中:T为动坐标系R′与固定坐标系R的坐标变换矩阵;α,β为动平台绕万向铰链两个转轴转动的姿态角。
将式(1)、(2)代入式(4)可得位矢Bi在基础坐标系R:OXYZ下的坐标为:
(5)
设机构3个移动副长度为li(i=1,2,3),则有:
(6)
将式(5)代入式(6)中并展开,可得:
(7)
由式(7)可进一步求解:
(8)
式(8)即为该并联机构的位置反解方程。
1.3 速度分析
设q为动平台输出速度向量,p为各支链的输入速度向量,且有:
(9)
(10)
则并联机构的速度约束方程写成:
Aq=Bp
(11)
式中:A和B为3×3矩阵。则式(11)可进一步写成:
q=Jp
(12)
式中:J为速度雅可比矩阵。
J=A-1B
(13)
对式(8)进一步求导整理可得2PUS-U并联机构动平台的速度方程:
(14)
整理后矩阵A和B可以表示为:

(15)
(16)
式中:
M=Rsβ-zcβ-zctφcθsβ,
N=z-rsβ+rctφcθcβ-Rctφcθ+zct2φ,
P=Rsα+zcαcβ-zsαctφsθ+zctφcθcαsβ,
Q=z+rsαcβ+rctφsθcα-Rctφsθ+zct2φ+rctφcθsαsβ。
根据式(13)可求出速度雅可比矩阵J,可知J与R,r,φ,θ,α,β和z有关,其中R,r,φ,θ是2UPS-PU并联机构的设计参数,α,β和z是动平台的位置和姿态参数。
2 优化数学模型
2.1 灵巧度评价指标
评价灵巧度的指标一般包括可操作度和条件数,利用可操作度评价存在一定的缺陷[12],因此本文采用雅可比矩阵的条件数作为评价2UPS-PU并联机构灵巧度的指标。雅可比矩阵条件数可表示为:
k=‖J‖‖J-1‖
(17)
式中:k为雅可比矩阵条件数,1≤k<∞。
如果速度雅可比矩阵的条件数较大,则该矩阵的逆矩阵J-1精度较低,此时利用式(13)求驱动器输入速度时,会使输入和输出速度之间的传递关系严重失真,另外驱动器的输入速度的微小偏差将会导致并联机构的输出速度出现较大偏差,因此在进行机构设计时,应该使得该机构速度雅可比矩阵的条件数在其操作范围内尽量为较小的值。当k=1时,并联机构具有最佳的运动传递性能,此时称并联机构的这一形位为运动学各向同性。当雅可比矩阵条件数为无穷大时,并联机构处于奇异形位,因此雅可比矩阵条件数可用来度量并联机构的灵巧度。
2UPS-PU并联机构输出速度向量中同时存在线速度和角速度,即有:

(18)
式中:ν为动平台的线速度向量;ω为动平台的角速度向量。由于ν和ω具有不同的量纲,利用雅可比矩阵J的条件数评价灵巧度不够准确,因此式(18)可以改写为如下形式:
(19)
式中:Jω,Jν分别为角速度和线速度雅可比矩阵。则Jω与Jν的条件数可定义为:
(20)

(21)
可以证明,对于2UPS-PU型并联机构,其kJν值恒为1,证明如下。
证明:
由式(9)~(12),可知:
(22)
由于在2UPS-PU型并联机构中,φ值不可能取0,因此:
(23)
因此矩阵Jν是行满秩矩阵,其广义逆为:
(24)
将式(22)代入式(24)后,可得:
(25)
则可得:
(26)
证毕。
由此可知,2UPS-PU型并联机构在线速度上是各向同性的,因此在优化上应使角速度条件数kJω尽量靠近1。单个kJω值是对应于动平台特定位置的,不能用来衡量整个运动空间的灵巧度,为此Gosselin等[13]定义了全条件性指标ηJω,用以评价机构在可达工作空间的角速度灵巧度:
(27)
式中:ηJω为机器人的角速度全条件性指标,0≤ηJω≤1;W为动平台的可达工作空间。事实上式(27)的数学意义是雅可比矩阵的条件数kJω的倒数在可达工作空间上的平均值。ηJω值越大,并联机构的灵巧度和控制精度越高。由于ηJω的精确解获取很困难,因此Pusey[14]定义了离散型全域条件数:
(28)

上述定义都是面向可达工作空间的,但实际上2UPS-PU并联机构的可达工作空间比较小,以图1中动平台参考系原点o为参考点,其可达工作空间为一条线段,长度由移动副L3的杆长限制。因此为了全面衡量机构的角速度条件数,还应考虑每一个可达位置上点的姿态,为此需要在全姿态空间[15]上进行定义。
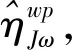
(29)
式中:wp为姿态空间上点的数目;分子为姿态空间网格中对应点的条件数的倒数之和。
2.2 数学模型
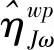
(30)
式中:Lmin≤Li≤Lmax(i=1,2,3)表示杆长限制;θHi≤θH max i(i=1,2,3)表示虎克铰限制;θSi≤θS max i(i=1,2)表示球铰限制。
3 基于人工蜂群算法的优化
3.1 人工蜂群算法
人工蜂群算法仿生蜜蜂群体采蜜时各个蜂种之间的配合,以找到最优采蜜位置。该算法控制参数少,全局寻优性好,收敛速度快,具有非常好的优化搜索特性,可以有效解决实际工程问题。
人工蜂群算法的搜索模型包括蜜源、引领蜂、跟随蜂和侦查蜂。其中,蜜源代表问题的可行解;引领蜂与蜜源一一对应,用来存储蜜源的相关信息,并将这些信息以一定的概率与其他蜜蜂分享;跟随蜂与引领蜂分享相关信息进行局部搜索找到新蜜源;搜索一定次数找不到更好的蜜源后,由侦查蜂进行随机全局搜索找到新蜜源,以跳出局部最优值。算法的具体步骤如下[16]:
Step1,初始化算法的基本参数(问题维数D、最大迭代次数ItMax、蜜源数目nPop、丢弃限度L,按照式(31)为每一个蜜源设置随机值:
Xi,j=Xmin,j+r(Xmax,j-Xmin,j)
(31)
式中:Xi,j为第i个蜜源代表的可行解中的第j维值,即原蜜源,其中i=1,…,nPop,j=1,…,D;Xmin,j,Xmax,j分别为第j维值的下限和上限;r表示[0,1]的随机值。
Step2,每一个引领蜂对相应的蜜源随机选择除本身以外的另一个蜜源,按照如下公式计算新蜜源的位置:
Vi,j=Xi,j+φi,j(Xi,j-Xk,j)
(32)
式中:Vi,j为新蜜源;Xk,j为随机选择的蜜源;φi,j表示[-1,1]范围内的随机值。用新蜜源的适应度值与原蜜源的适应度值比较,如果大于则更新,否则计数加1;
Step3,每一个跟随蜂按照轮盘赌法选择一个蜜源,再随机选择一个除本身以外的蜜源,按照式(32)局部搜索新蜜源,计算新蜜源的适应度值,如果大于原蜜源适应度值则更新,否则计数加1;
Step4,侦查蜂检测每个蜜源的更新计数,如果连续L次没有得到更新则抛弃蜜源在全局重新搜索;
Step5,记录一次迭代找到的最优蜜源,比较是否达到终止条件,如果达到则输出最优值,否则回到Step2。
将上述过程利用MATLAB编程实现,并在MATLAB R2012平台上进行计算。
3.2 适应度函数
对并联机构结构参数进行优化的关键是制定适应度函数。按照上文给定的数学模型,给出适应度函数的算法。
算法1,并联机构在姿态空间的适应度值。
输入:并联机构设计参数X=[R,r,φ,θ]。
步骤:
1)初始化。
{给出动平台姿态定义域范围[αmin,αmax],[βmin,βmax],[zmin,zmax],杆长限制范围[Lmin,Lmax],胡克铰最大转角,球铰最大转角,随机搜索点数N1,并将计数器N2初始化为0};
2)采用蒙特卡洛方法在动平台姿态定义域{[αmin,αmax],[βmin,βmax],[zmin,zmax]}内随机搜索N1个点;
3)For(i=1;i<=N1;i++)do
{
判断是否符合杆长和最大转角限制;
如果符合则
{
N2=N2+1;
计算该点的角速度条件数kJω;
}
}
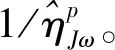
将上述过程也用MATLAB编程,作为人工蜂群算法的适应度函数。
3.3 优化结果
2UPS-PU型并联机构的设计约束设置见表1。

表1 结构参数范围
人工蜂群算法初始参数设置如下:D=4,ItMax=100,nPop=20,L=5。
按照上述设置,得到如图2所示优化迭代过程。

图2 优化迭代过程

4 优化结果分析
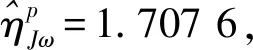

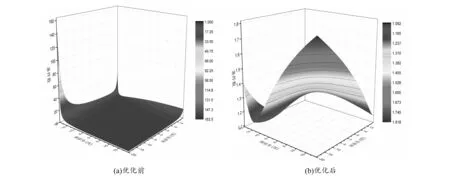
图3 z=780 mm平面角速度条件数分布对比

图4 z=850 mm平面角速度条件数分布对比

图5 z=1 200 mm平面角速度条件数分布对比
5 结论
本文对一种少自由度2UPS-PU并联机构的结构参数以角速度离散型全姿态空间条件数为指标采用人工蜂群算法进行优化设计,得到了以下结论:
1)优化后2UPS-PU并联机构在动平台的全姿态空间内灵巧度显著改善,避免了运动传递过程中的失真现象,为抗眩晕训练装置物理样机的设计和制造提供了理论和技术支持;
2)角速度离散型全姿态空间条件数的评价指标考虑到并联机构可达工作空间每一点的所有姿态,计算量小,为并联机构的灵巧度优化提供了有效的评价指标;
3)人工蜂群算法适用于并联机构的优化设计,全局搜索能力强,收敛速度快。
