风电传动系统轴承多目标优化设计

袁海良，邱 俊，王 智，王德伦

(大连理工大学机械工程学院, 辽宁 大连 116024)

作为风力发电机组的核心部件，主轴传动系统轴承的性能直接影响轴系的安全性、稳定性。设计轴承的过程中，评价指标不同会导致轴承结构参数的差异。目前，轴承结构设计的效率低、周期长，如何改进轴承的设计方法成为提高轴承结构设计效率的关键。

近年来国内外学者对轴承的优化设计均做了相关的研究。文献[1]通过ISIGHT与MATLAB软件的联合运用完成双列圆锥滚子轴承(DTRB)的优化设计；文献[2]将改进的自适应遗传算法应用于圆锥滚子轴承的优化设计；文献[3]基于遗传算法进行了双列圆锥滚子轴承的优化设计；文献[4]综合研究了双列圆锥滚子轴承的受力及润滑状况；文献[5]在实验数据和理论模型的基础上，将有限元法与多响应面优化相结合，寻找到双列圆锥滚子轴承的最佳运行工况；文献[6]基于FEM(finite element method)与RSM(response surface methodology)对圆柱滚子轴承(CRB)进行优化设计；文献[7]借助MATLAB的fmincon命令完成圆柱滚子轴承的优化设计；文献[8]运用遗传算法完成了圆柱滚子轴承的优化设计；文献[9]运用人工蜂群算法完成了圆柱滚子轴承的多目标优化设计。当前的研究方法多数只考虑单目标优化，且未综合考虑轴系中的全部轴承。为此，本文以某型号双馈式风电机组的轴系为例，在综合考虑全部轴承的基础上，建立其优化的数学模型，借助MATLAB实现轴承的结构参数优化设计。

1 结构式与力学模型

风机主轴系有各种不同的结构[10]，如图1所示为双馈式机型中典型的轴系结构，双列圆锥滚子轴承与圆柱滚子轴承构成载荷支点，支撑转轴从而构成轴系，转轴的法兰与风机轮毂连接，载荷由轮毂传递至轴系。

图1 典型轴系结构示意图

主轴与齿轮箱之间通常采用柔性连接，抽象简化出的轴系力学模型如图2所示，图中O点为法兰载荷作用点，其坐标系参考GL规范[11]要求，O1和O2为轴承载荷点，L1和L2为各载荷点之间的距离；Mxm,Mym,Mzm,Fxm,Fym,Fzm为外载荷，Fx1,Fy1,Fz1为O1支点的载荷，Fx2,Fy2,Fz2为O2支点的载荷。

图2 轴系力学模型图

将空间力系转化为Oxy与Oxz平面力系，以O点为坐标原点，得到平面内O1和O2点的载荷。

在Oxy平面内FOxy为：

(1)

在Oxz平面内FOxz为：

(2)

由此得到O1点与O2点轴承的径向力为：

(3)

式中：FO1与FO2分别为O1,O2点的载荷。

对于轴向力，当O1支点为DTRB时，Fx1=Fxm,Fx2=0；当O1支点为CRB时，Fx1=0,Fx2=Fxm。根据以上力学分析，得到轴承承受的载荷FB为：

(4)

式中：Ftd,Ftr分别为DTRB的轴向力与径向力；Fcd,Fcr分别为CRB的轴向力与径向力；A为2×2阶矩阵，当A为单位对角矩阵时，表示O1支点为DTRB，当A为单位反对角矩阵时，表示O1支点为CRB。

2 优化模型

轴承的体积、寿命均为评价轴承设计结果的指标，体积反映了生产轴承所消耗材料的量，寿命反映了轴承运行时间的长短。

在轴承中，套圈与滚子存在配合关系，因此其尺寸参数之间相互制约。将尺寸变量分为自变量与相关变量，套圈内外径、厚度等参数在设计时可以在一定的范围内变动，则这些尺寸参数为自变量；滚子直径、长度等参数可以根据套圈等的尺寸得到，则这些尺寸参数为相关变量。

优化模型需要确定5个方面的问题：目标函数、约束函数、优化变量、优化算法以及结束准则。

建立目标函数与约束函数时，为了避免轴承相同参数表达的冗余，以下角标i表示轴承类型，i=c,t，其中c表示CRB，t表示DTRB。

2.1 目标函数

目标函数是优化模型中的核心内容，需要清晰而又准确地建立。考虑到DTRB结构的对称性，以单列轴承为基础进行分析，图3所示为轴承结构示意图。

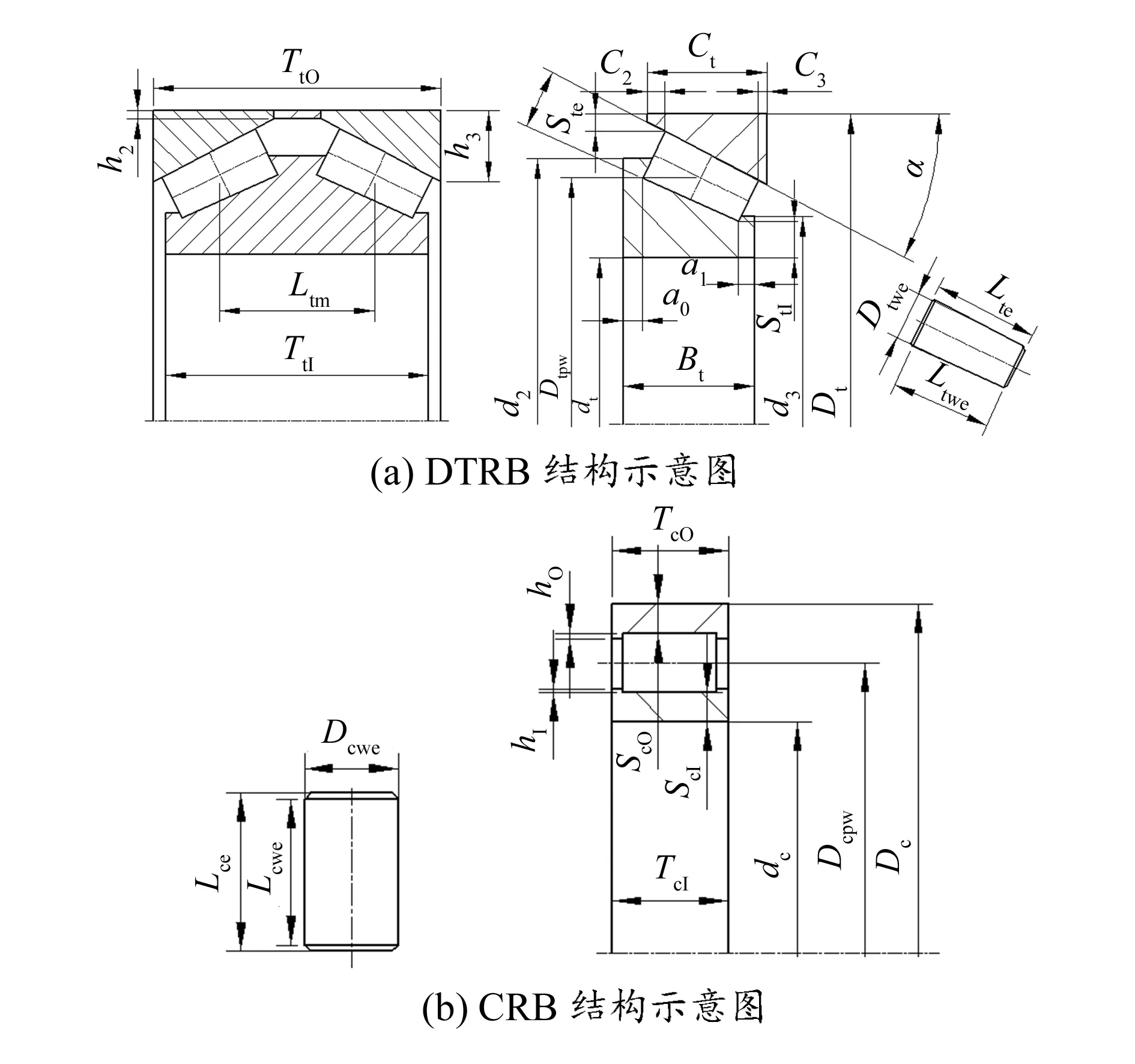
图3 轴承结构示意图

1)轴承体积。

轴承的体积越小，生产时消耗的材料越少，因此可以选择轴承体积作为优化目标。对于体积函数，尺寸变量在定义域内的迭代变化必然引起函数值的改变，函数值的减小意味着轴承体积减小。

轴承体积VA为CRB与 DTRB体积的代数和：

VA=Vio+Vii+ViR

(5)

式中：Vio为外套圈体积；Vii为内套圈体积；ViR为滚子体积。

2)轴承寿命。

在轴承设计中，寿命是评判轴承的重要标准，寿命值越大，则轴承可运转时间越长，因此可以选择轴承寿命作为优化目标。轴承寿命与其结构尺寸之间的关系为非线性关系，尺寸变量在定义域内的迭代变化必然引起函数值的改变，函数值的增大意味着轴承寿命延长。

根据ISO281标准[12]，轴承修正寿命Lim表示为：

(6)

式中：Ci为基本额定动载荷；Pi为当量动载荷；αi1为可靠度寿命修正系数；αiISO为寿命修正系数。

由于CRB、DTRB的结构与承受载荷的差异，一般情况下两个轴承的寿命并不能保证相同，因此轴承寿命LA以其中最小者为准：

LA=min(Lcm,Ltm)

(7)

2.2 约束函数

轴承的结构尺寸必须保证轴承工作时运转顺畅，各部分之间不存在干涉，同时为了确保工作时机组的安全性，轴承需要满足相应的性能要求。

考虑轴系的装配关系，O2处轴承内径必须小于O1处轴承内径：

Ψcdc+Ψtdt≤0

(8)

式中：Ψc,Ψt为控制O1,O2处轴承内径关系的系数，且[Ψc,Ψt]=A[1,-ξ]T，ξ∈(0,1)。

对于风电机组的CRB，内圈厚度Cc与外圈厚度Bc一般相同：

Cc-Bc=0

(9)

对于风电机组的DTRB，根据滚子与套圈的配合关系，可以得到：

(Bt-a0-a1)cosα+(Ct-C2-C3)cos(α-2φ)=0

(10)

式中各参数的含义如图3所示。

轴承结构既要保证滚子不碰撞，又要避免滚子分布过于稀疏，因此根据滚子分布的几何关系可得：

(11)

式中：Zi为滚子个数；Diwe为滚子直径；Dipw为滚子节圆直径；kmin,kmax分别为滚子分布系数的最小值和最大值。

为了保证滚子外形的协调，滚子直径与滚子和轴承滚道的有效接触长度之间需要满足：

Ψmin≤Diwe/Liwe≤Ψmax

(12)

式中：Ψmin,Ψmax为比例系数的最小值和最大值；Liwe为滚子接触长度。

根据赫兹接触理论，轴承滚子的接触应力σi可表示为[13-15]：

(13)

式中：Qimax为轴承的最大接触载荷；E1,E2分别为滚子和套圈的弹性模量；ν1,ν2分别为滚子和套圈的泊松比；Ri1,Ri2分别为滚子和滚道的半径。

为了避免滚子与滚道之间接触应力过大而损坏轴承，需要保证接触应力小于等于其许用值：

σi-[σi]≤0

(14)

式中：[σi]为接触应力许用值。

根据德国劳埃德船级社风力发电机组认证规范(GL认证)，风机轴承设计寿命至少20 a[12]，因此设计轴承时必须将其寿命作为约束条件。当选择寿命为优化目标时，表示在满足许用要求的条件下，寿命最长。

[LA]-LA≤0

(15)

式中：[LA]为寿命许用值。

2.3 设计变量

设计变量是求解优化模型过程中需要优化的参数。由于结构尺寸变量中的自变量能够引起相关变量的改变，因此将自变量选定为设计变量。

对于CRB，内径(dc)、外径(Dc)、内套圈宽度(Tci)、外套圈宽度(Tco)及滚子个数(Zc)能够确定CRB的其他尺寸变量，因此将这些参数作为自变量。

对于DTRB，内径(dt)、外径(Dt)、单列内套圈宽度(Bt)、单列外套圈宽度(Ct)、接触角(α)、锥角(φ)及滚子个数(Zt)能够确定DTRB的其他尺寸变量，因此将这些参数作为自变量。

综上，设计变量X为：

X=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12]=[dc,Dc,Tci,Tco,Zc,dt,Dt,Bt,Ct,α,φ,Zt]

(16)

对于工程类问题，设计过程中需要考虑尺寸参数的范围。DTRB的接触角一般为25°左右，因此其定义域为α∈[20°,30°]；取DTRB锥角的定义域为φ∈[1°,4°]；其他变量均为结构尺寸参数，取值范围均为大于0，计算时可依据外载荷预估给定。

2.4 算法与初始值

优化算法选择的依据是优化数学模型的类型。本文首先采用目标达到法将多目标优化问题转换为单目标优化问题，然后采用单目标优化方法进行求解。多目标优化问题转换后的数学模型为：

(17)

显然优化数学模型为非线性约束优化问题，序列二次规划法(SQP)是求解此类问题的有效方法，因此本文选择此方法。

一般情况下，目标函数具有多个局部最优解，当初始值位于最优解附近时，迭代就能够收敛。但是在计算时很难直接将初始点设置于最优解附近，因此本文中依据变量的范围随机生成初始值。

2.5 结束条件

算法需要满足设定的结束条件才可以停止迭代。选取以下条件，当迭代满足任一条件时，算法迭代即停止。

条件1：相邻幂次两个变量迭代结果之间的距离满足允许精度，即

‖Xk+1-Xk‖≤ε1

(18)

式中：Xk+1与Xk为相邻幂次两个变量迭代值；ε1为允许精度。

条件2：函数在迭代点处的方向导数满足允许精度，即

(19)

3 算例分析

已知某型号主轴轴承的设计参数，见表1，要求根据表中的参数设计出轴承结构。

表1 轴承设计参数

依据定义域设置变量的范围，见表2。

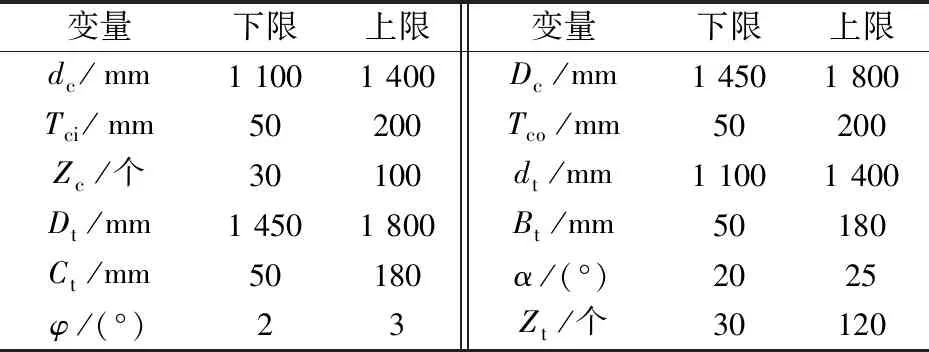
表2 变量范围

一般情况下，优化目标不同则优化结果不同，分别对单目标与多目标进行优化。借助于MATLAB进行求解，操作流程如图4所示。

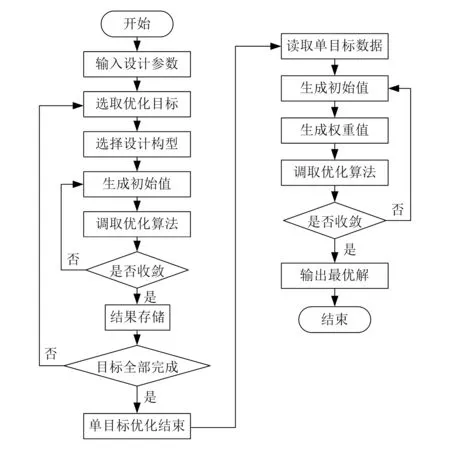
图4 操作流程图

对两种结构轴系的轴承进行单目标优化，优化目标分别为体积和寿命，迭代计算结果见表3。由表中的数据可知，CRB+DTRB轴系结构优于DTRB+CRB轴系结构。

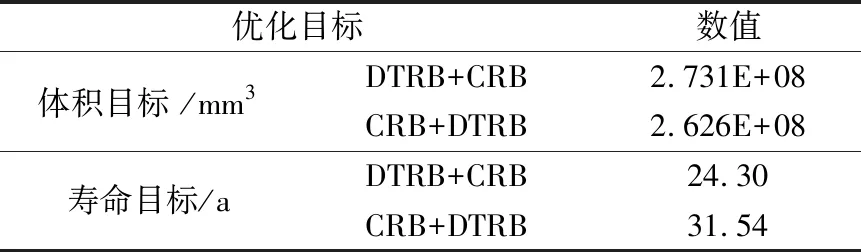
表3 不同结构轴系优化结果

一般在进行多目标优化时，各个目标之间会相互制约，一个目标的最优是以牺牲其他目标为前提，因此多目标优化不可能使所有的目标都得到最优值。以DTRB+CRB轴系结构为例，分别进行单目标优化与多目标优化，优化结果见表4。

表4 单目标与多目标评价指标结果

由表4可知，多目标优化的结果均介于单目标优化的结果之间，表明多目标优化在迭代计算过程中能够均衡各个目标。

以DTRB+CRB轴系结构为例，分别对DTRB与CRB进行单独优化计算，结果见表5。

表5 单独优化评价指标结果

对比轴系单独优化与综合优化结果发现，寿命结果相近，且均能够满足许用要求；综合优化的体积值优于单独优化的值，表明综合优化时算法能够同时迭代优化变量而得到更优的结果。

为验证使用本文方法得到的轴承的合理性，选取以体积为单目标的DTRB+CRB轴系结构的优化结果，借助RomaxDesigner进行校核验算，分别得到极限与疲劳载荷作用下的滚子与滚道的接触应力，如图5～8所示，图中数据显示设计结果满足要求。

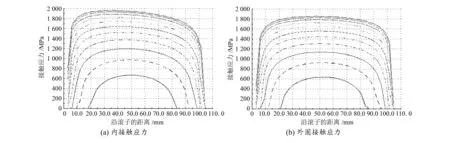
图5 DTRB极限载荷接触应力

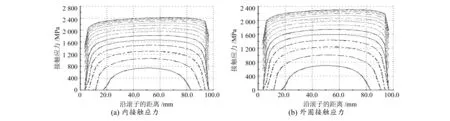
图6 CRB极限载荷接触应力

图7 DTRB疲劳载荷接触应力

图8 CRB疲劳载荷接触应力

4 结论

本文建立了某典型风机主轴系结构的力学模型与优化数学模型，在单目标优化模型的基础上，耦合出多目标优化模型。以某型号风电机组为例进行优化计算，通过对结果的分析与验算得到如下结论：

1) 轴系设计时，结构的选择需要考虑侧重于何种优化设计目标，本文以不同优化目标进行优化得到的最优轴系结构均为CRB+DTRB。

2)与单目标优化相比，多目标优化不能保证所有优化目标都能够达到最优值，但是能够权衡考虑各个优化目标。

3)相比于对DTRB与CRB单独优化，对DTRB与CRB进行整体优化能够综合考虑两个轴承而使得结果更均衡、优化目标更优。

4)运用RomaxDesigner对所设计的轴承进行验证，结果表明轴承设计结果是合理的。