环氧树脂/594体系固化反应动力学研究*

方双全, 秦云晴, 俞 亮，翁 辉

（扬州大学机械工程学院，江苏扬州 225127）

环氧树脂（EP）因为其硬度高、固化收缩性小、附着力强等特性，被制成涂料、复合材料、胶粘剂，被广泛应用于航空航天以及热固性材料等国民经济的各个领域[1-3]。关于固化动力学研究，科研工作者已对环氧树脂固化性能的方面做了大量的工作，例如，高婧韬等[4]总结了潜伏型固化剂2-甲基咪唑对环氧树脂的固化影响，发现E-51/2-MI体系固化过程符合Kamal复合模型。左联等[5]采用E-51型环氧树脂与固化剂（三乙烯四胺）进行固化反应，得出大体积环氧树脂在固化时的温升变化规律及性能。Yousefi等[6]利用动态和恒温DSC技术获取环氧树脂样品热量吸收或释放的谱图，推导出固化反应的初始、峰值和结束温度。李恒[7]利用作图法得到反应活化能 Ea、反应级数n和m,并根据反应活化能的变化规律分析固化反应机理的变化。常温时，潜伏型固化剂与环氧基团即便处于均匀混合状态下，也能够稳定的贮存一段时间，固化交联反应只有在达到固化剂需求的情况下发生，因此借助这个特性，可以通过将固化剂和环氧树脂混合均匀后出售或运输，以此降低成本和操作步骤。本文通过非等温DSC法对环氧树脂掺杂不同比例的固化剂在不同升温速率下的固化过程进行了研究，获得环氧树脂基体的动力学参数，可为环氧树脂固化过程提供实验支撑与理论依据。

1 实验部分

1.1 主要原料及设备

原料：环氧树脂（E-51），固化剂（594），来自无锡仁泽化工产品有限公司

设备：差示扫描量热仪，型号DSC8500，来自美国PerkinElmer。

1.2 性能测试

将E-51与固化剂594按照特定比例混合，机械搅拌30min，得到测试样品。使用差示扫描热分析仪测试，每次取试样10mg左右放入测试锅中，参数设置为：升温速率分别为2.5℃/min、5℃/min、10℃/min和20℃/min，升温范围为24℃～280℃。

2 结果与分析

2.1 DSC曲线分析

图1分别是594用量为7%、8%、9%、10%、11%的E-51/594体系在不同升温速率下测得的固化反应DSC曲线。

图1 不同固化剂用量下的树脂体系非等温固化DSC曲线Fig.1 Non-isothermal curing DSC curve of resin system under different curing agent dosages

从图1中可以直观地看出，E-51/594体系在不同升温速率下的趋势是相同的，均得到了单一的放热峰，并且随着升温速率的升高，各个体系的放热峰向高温区移动，特征温度也随之增高，说明在低升温速率进行升温固化时，树脂固化体系有足够的反应时间，随着升温速率的提高，热效应增大，体系的热惯性变大，导致温差也越大，因而放热峰逐渐进入到了高温区。取实验所得特征温度（包括起始温度、峰值温度和终止温度）进行线性拟合，横坐标为升温速率，纵坐标为固化特征温度，将拟合线外推至零，就得到了拟合的等温固化温度。将结果汇总于表1中。由表中数据可知，发现含有10%固化剂时的反应开始的温度最低。

表1 E-51/594固化体系等温固化温度Table 1 E-51/594 curing system isothermal curing temperature

本文选取固化剂含量10%的环氧树脂体系作为研究目标，计算体系的固化动力学参数和方程。

2.2 固化反应动力学参数

表观活化能Ea和指前因子A的确定：

固化的难易可通过表观活化能来了解，活化能越小则越易固化，反之则越难固化。本文通过以下两种方法来求活化能

Kissinger[8]方程：

式中：ß（℃/min），升温速率；Tp（℃），峰值温度；E（kJ/mol），表观活化能；A，指前因子；R，理想气体常数，8.314J/(mol·K)。依据表1中的数据，把对1/Tp作图[图2(a)]，通过线性拟合的方法得到直线的方程为：y=-1.75×103x+0.226，再根据上述方程得到Ea=14.74 kJ/mol，由截距可得到指前因子A=4.55×105。

Ozawa[9]方程：

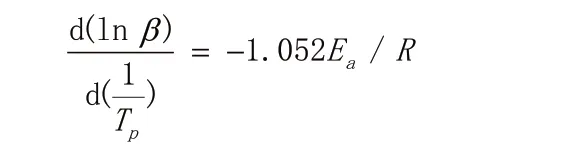
依据表1中的数据，作图[图2(b)]，lnβ纵坐标，1/Tp横坐标，通过线性拟合的方法得到直线的方程为：y=-2.15×103x+12.81，由Ozawa方程显示，得到的斜率可求得体系的表观活化能，Ea=15.27 kJ/mol。

两种活化能的差异可能是不同假设条件导致的，这里取两种活化能的平均值，即Ea=15.21 kJ/mol。

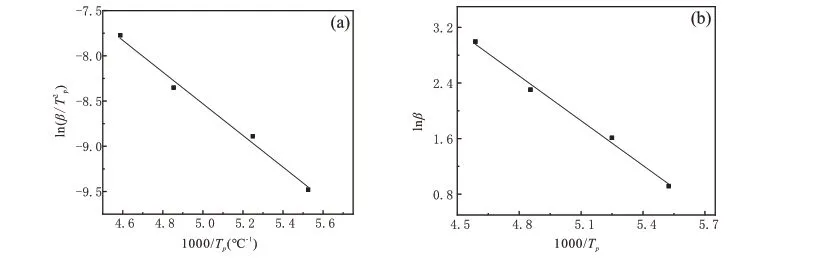
图2 树脂体系固化反应线性拟合线：(a)Kissinger方程(b)；Ozawa方程Fig.2 Linear fit line of curing reaction of resin system:(a) Kissinger equation；(b) Ozawa equation

2.3 固化反应动力学模型

常用的经验模型是自催化反应模型，本文即采用此模型对EP固化反应的固化反应级数和动力学模型进行了研究。模型的表达式[10]如下所示：

式中：n、m为反应级数，k(T)为反应速率常数，即：

Crane[11]方程如下所示：

把lnß对1/Tp作图，通过线性拟合的方法就能得到反应级数n。

自催化反应模型（又叫双参数模型），增加了参数，提高了精度，能更加精准的反应固化过程。为了增加计算结果的可靠性添加两个特殊的方程y(α)和z(α)[12-13]，表达式如下：

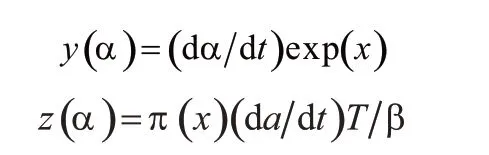
式中：x=Ea/RT，温度的积分形式，采用Senum和Yang[14]提出的近似表达式进行计算：

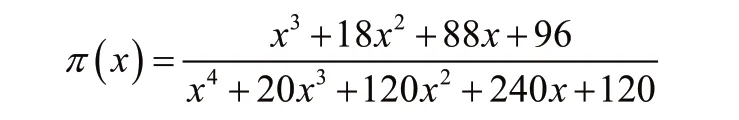
作y(α)-α、z(α)-α的 曲 线，找出y(α)、z(α)最 大 值时对应的固化度，将它们分别记为αM和 Pα∞。对DSC曲线进行微分处理，可得dα/dt与α的函数关系图，将数据代入式中可得y(α)、z(α)与α的函数关系图，如图3、图4所示。

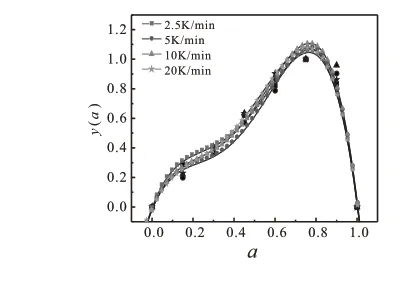
图3 y(α)-α函数关系Fig.3 y(α)-αFunction Relationship

图4 z(α)-α函数关系Fig.4 z(α)-αFunction Relationship

从图3、图4中可以看出，不同的升温速率下的固化程对应的αM和的值基本保持稳定。在αMM∈(0,1)，同时的前提条件下，由y(α)和z(α)的特征值可以得知，自催化动力学模型足以表达E-51/594体系的固化过程，表达式如下所示。

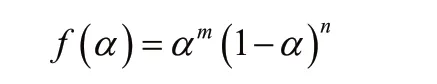
可改写为：

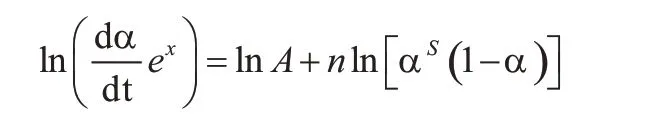
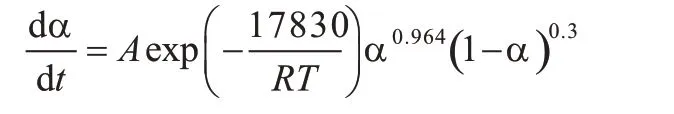
最大概然机理函数法常用于固化反应计算，这个方法得到的固化反应模型是否可以表达E-51/594固化体系的固化反应过程，可以将计算所得的曲线（dα/dt与T的曲线）和实验所得的曲线进行对比得出，如图5所示。

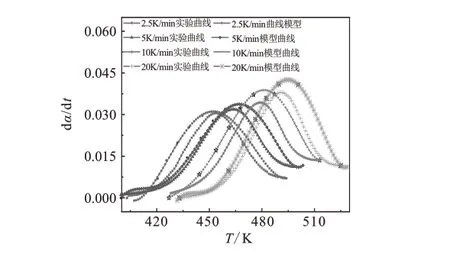
图5 实验测试曲线与固化动力学模型计算曲线对比Fig.5 Comparison of experimental test curve and calculation curve of curing kinetics model

观察图5可以发现，不同升温速率下的模型曲线和实验曲线的重合率非常高，说明自催化模型能够很好地表达固化过程，于是可以通过计算得到的模型来对实验体系进行一个很好的预测，这能够大大降低前期投入的成本和人力。对图5进行一个更加细致的观察发现前期和后期时模型曲线的吻合情况有一定的波动。前期基本能够与实验数据保持一致，而后期吻合情况稍差，这是因为反应后期，整个体系的粘度渐渐增大，阻碍了体系中未反应的分子的扩散，从而影响到整体反应的趋势，而模型模拟出的曲线并未考虑到这方面的影响。

3 结论

（1）由非等温DSC实验曲线，分析后得到了594固化剂在5种配比下的环氧树脂体系的反应起始、峰值和终止温度。

（2）对比不同固化剂含量下体系的固化温度和活化能可得到，当固化剂比例达到10%时体系的固化起始温度最低，所需的固化反应的活化能也较低，是E-51/594体系的最佳比例。

（3）环氧树脂/594体系固化动力学方程为