海外600 MW机组工程低频振荡分析及解决方案

黄晓鹏，丁永允，段海洲，魏 来，赵帅达

(1.辽宁东科电力有限公司，辽宁 沈阳 110179；2.国网辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006；3.沈阳工程学院，辽宁 沈阳 110136)

1 故障概述

海外某600 MW机组在调试升负荷过程中发生低频振荡，振荡时有功功率380 MW，无功70 Mvar，现场未进行PSS试验。振荡频率为0.4 Hz左右，振荡过程持续7 min，起初有功波动幅值为60 MW左右，由于振荡一直未平息，最终振幅达到200 MW，导致系统故障，机组与系统解列，并造成全厂失电。

此项目为2×600 MW机组工程，当前电网结构并未完善，机组处于电网末端，通过400 kV变电站经200 km架空线路与2台350 MVA联络变压器相连，再经132 kV线路向132 kV系统供电。

励磁系统采用UNITROL6800励磁调节器，励磁系统主要参数见表1，电力系统稳定器采用PSS-2B型，发电机主要参数见表2。

表1 励磁系统主要参数

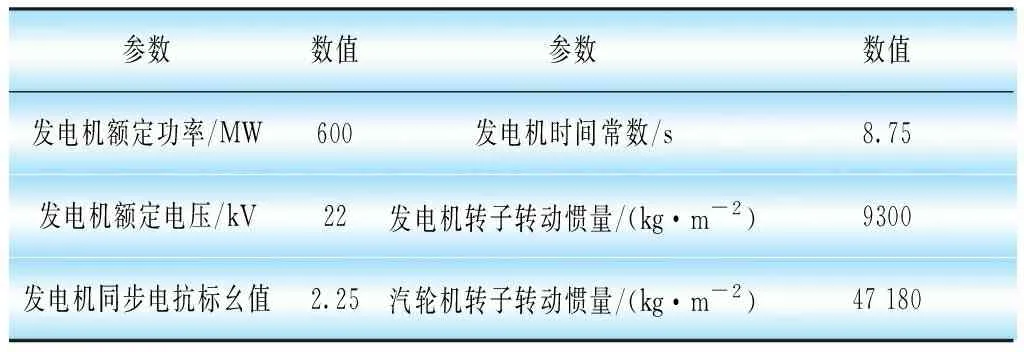
表2 发电机主要参数

2 低频振荡原因及项目特点

低频振荡主要有区域间振荡和局部振荡2种类型。前者是系统的一个区域机群对于另一个区域机群的振荡，振荡频率一般较低，在 0.1～0.7 Hz。局部振荡是电气距离较近的少数发电机之间的相互振荡，这类振荡局限于区域内，频率为 0.7～2 Hz。

2.1 引起功率低频振荡的主要原因

图1为原动机调节系统的phillips-Heffron模型，由此模型可知,引起ΔP振荡的原因主要是励磁系统和调速系统，文献[1]介绍了由调试系统引起的低频振荡。根据现场对调试系统的检查，当系统发生低频振荡时，汽轮机蒸汽调节阀变化幅度较小，变化幅度不足以引起有功功率的大幅变化，因此排除此台机组由于调速系统引起的低频振荡。

图1中，K1、K2、K4-K6随运行方式变化而变化。通常K1、K2、K4、K6为正值；当负荷大于某一数值时，K5可能由正值变为负值。

(1)

式中：KA为励磁系统动态放大倍数。

负荷较轻时，K5>0，附加阻尼转矩ΔTD>0，长距离、重负荷输电时，K5<0。励磁系统动态放大倍数越大，ΔΤD越小，从而引发电机的增幅振荡。一般而言，对于远距离、大负荷送电的快速励磁系统，如果K5<0，就会影响系统阻尼。一旦受到小扰动后，电力系统有可能发生自发振荡和非同期性的失步，这种振荡是0.2～2.5 Hz范围内的低频振荡。

2.2 项目特点分析

2.2.1 与系统联系强弱

a.联系阻抗Xe计算

(2)

式中：U1、U2和Q1、Q2是电压和无功前后2次的测量值，一般认为Xe<0.2时，发电机与系统联系紧密，经计算Xe=1.0。

b.电压+2%阶跃试验

发电机有功功率为350 MW，在电压2%阶跃试验中，发电机有功功率振荡次数超过10次。当振荡过程中阻尼比小于0.1时，振荡将超过5次，认为阻尼较弱；当阻尼比小于0.05时，振荡将超过10次，称为弱阻尼；当阻尼比为负值时称为负阻尼，将产生自发振荡。结合系统阻抗的计算基本可以判断此台机组系统为弱联系。

2.2.2 励磁系统高增益

励磁系统为自并励磁系统，采用PI控制，动态增益与暂态增益相等，负载2%阶跃试验结果计算励磁系统动态增益为

(3)

通过上述分析此项目符合系统弱联系、励磁系统高增益、发电机输送大功率的特点。因此判断在当前的电网结构且为高负荷运行情况下极易发生低频振荡。

3 PSS现场试验

3.1 试验工况选取

DL/T 1231—2018《电力系统稳定器整定试验导则》(简称导则)要求：此项目试验工况为有功负荷大于396 MW，无功功率小于80 Mvar。依据现场380 MW期间发生低频振荡事故分析，在当前的电网结构下，机组有功负荷达到380 MW时，有功功率在0.3 Hz振荡时，系统阻尼基本为零。由图4 可知，350 MW试验工况下，0.5 Hz振荡时，系统阻尼仅为0.02。文献[2]介绍了运行工况对电力系统稳定器PSS现场参数的整定影响，PSS参数整定试验应尽量在接近额定有功功率的工况下进行。如果因条件限制试验机组无法达到额定有功出力，则在参数整定时应适当缩小补偿范围，以保证PSS在额定有功出力下能满足补偿要求。因此根据现场的实际情况，试验工况选取有功负荷为350 MW，无功功率小于80 Mvar。

3.2 励磁系统无补偿特性

通过COCO-80X动态信号分析仪产生白噪声信号，接入调节器信号相加点，将机端电压信号经交直流变换后，接入COCO-80X输入通道，缓慢增加白噪声幅值，直至发电机机端电压有轻微摆动，进行参数测试。根据导则，通过调整PSS相位补偿，使附加力矩在0.1～0.3 Hz(不含0.3 Hz)频段，超前Δω轴不应大于30°，在0.3～2.0 Hz频率的力矩向量在超前Δω轴20°至滞后Δω轴 45°之间，同时PSS不应引起同步力矩显著削弱而导致振荡频率进一步降低、阻尼进一步减弱。试验及参数整定结果如图2所示。

3.3 PSS临界增益测试

观察PSS输出为零时投入PSS，观察励磁调节器的输出或发电机转子电压有无持续振荡。如无持续振荡则增大PSS增益，直至励磁调节器的输出或发电机转子电压出现微小、持续振荡时为止，此时的增益即为临界增益，通过试验临界增益测定为15。PSS运行增益取临界增益的20%～30%，即取PS1=3～5作为运行增益。

3.4 负载阶跃试验

进行有、无PSS的阶跃试验，计算有功功率振荡频率和阻尼比，当振荡频率不符合要求时应调整 PSS 相位补偿参数，当阻尼比不符合要求时应增大增益，再次进行有 PSS的阶跃试验直至满足要求。有、无PSS现场2%电压阶跃响应曲线如图3所示。

从表3和图3可知，有PSS比无PSS的负载阶跃响应的阻尼比应该明显提高，在350 MW试验工况下，当KS1=5时负载阶跃响应的阻尼比大于0.1。PSS整定参数见表4。

负载阶跃响应激发振荡频率为0.53 Hz，属于区域间振荡，其原因为当前电网结构和机组占比较高所致。

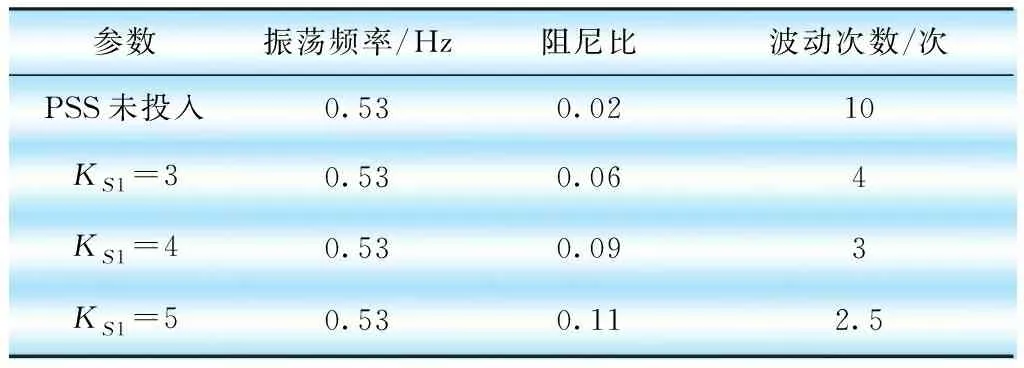
表3 振荡品质参数

表4 PSS整定参数

3.5 投入PSS前后的机组运行期间有功振荡及反调情况

表5为机组运行若干天有无PSS最大振幅的记录，并结合表3的试验结果初步得到结论：有无PSS，结果相异，这说明本机组的振荡参与度很高，属于振荡重点控制机组，在本机组增加投入PSS绝对有效果。

a.当前电网结构下，未投入PSS，有功功率在380 MW以上时，系统阻尼基本为零，极易发生低频振荡，振荡过程无法平息，最终导致跳闸。

b.PSS中的增益KS1=5投入过程中比KS1=3对有功低频振荡的抑制效果更好，而且励磁调节器输出的波动幅值适当。

c.PSS中的增益KS1=5投入，在负荷达到530 MW，发生系统扰动后，机组有功振荡明显加剧。因此基本可以判断目前励磁系统及PSS参数很难在当前电网结构下、530 MW以上负荷稳定运行，极易发生低频振荡。

d.进行无 PSS下的改变原动机出力试验，观察有功功率和无功功率波动。PSS-2B模型有转速信号参与调节，能够有效抑制反调现象。在运行期间，增减有功过程中，无功反调幅度很小，小于20%额定无功功率[2]。

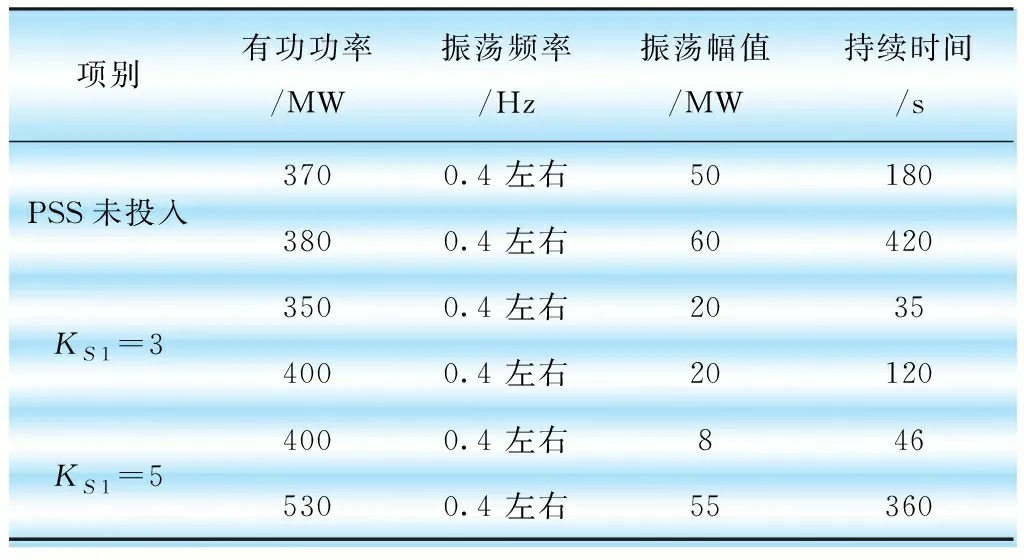
表5 投入PSS前后机组运行过程中有功振荡对比

4 提高系统阻尼的方案

由于发电机连接的系统为临时过渡系统，振荡频率基本集中在低频段0.3～0.6 Hz，目前主要目标为完成机组满负荷运行24 h要求。因此优化方案主要包括继续提高现有PSS的增益；进行PSS超前滞后环节第三阶整定[3]，有效增加低频段的增益；降低励磁系统动态增益，增加PSS增益。

4.1 提高PSS增益

PSS是个闭环控制系统，增加PSS增益可以增加机电振荡模式阻尼，减小电气振荡模式的阻尼。增益过大会引起电气振荡模式振荡的负阻尼，使系统失稳，电气振荡的频率一般为3～7 Hz，因此PSS中的KS1受限于励磁系统的电气振荡特性[4-5]。临界增益试验过程中，导则要求发电机转子电压出现等幅或接近等幅值振荡为止。文献[3,6]在临界增益现场试验过程中转子电压均波动超过当前值的15%，而本项目试验过程中，KS1=15时仅仅为轻微的转子电压波动。因此临界增益的提升还有一定余量，增加增益的同时，可以重点观察电气振荡的情况。

4.2 降低励磁系统动态增益

由式(2)可知，机组高负荷运行时，阻尼转矩ΔΤD为负，降低励磁系统动态放大倍数，可减小附加阻尼转矩ΔΤD，从而增加阻尼。由于PSS是个闭环控制系统，降低动态放大倍数的同时，可以相应提高PSS的临界增益，最终达到提高系统阻尼的目的。根据DLT 843—2010 《大型汽轮发电机励磁系统技术条件》，励磁系统的动态增益不小于30。

4.3 进行PSS超前滞后环节第三阶整定

现有参数整定方法在高频段增益的上翘造成了整体增益裕度偏小，导致了低频段模式下运行增益不足的问题。如能够在低频段时保持增益不变，同时降低高频段最高增益，就可以提高整体的增益稳定裕度。利用现有PSS-2B的第3个超前滞后补偿环节，可以在不改变中低频段的增益同时，降低最高增益值，提高整体增益裕度。对于超前滞后环节(1+T10s)/(1+T11)，当设置成T11>T10时，其相频特性滞后，幅频特性是衰减的。设计目标为减小0.1～2 Hz滞后角度同时，尽量减小3 Hz以上增益。因此超前滞后环节选为(1+0.06s)/(1+T0.09s)进行仿真试验。

5 仿真分析

采用PSASP程序，利用机组参数和模型建立单机无穷大系统，进行此项目定性仿真分析。仿真工况：有功功率为400 MW，无功功率为80 Mvar，机端电压为额定电压。励磁系统采用表1参数，PSS参数采用表4参数。

5.1 降低励磁系统动态增益仿真分析

仿真试验中，逐步增大参数组1和2中的参数Ks1值，当转子电压发散时，为负阻尼模式，此时Ks1为临界增益。参数组1中临界增益为35，整定增益为7；参数组2中临界增益为47，整定增益为9.4。

从图4及表6可知，参数组3和参数组4为未投PSS情况下，随动态放大倍数的降低，阻尼比随之降低，振荡频率也随之降低。参数组1和参数组2为PSS投入时，随着动态放大倍数的降低，PSS临界增益增加，PSS增益会增加，阻尼比基本不变，振荡频率随之降低。通过仿真结果表明，无法通过降低动态放大倍数的方法提高系统阻尼。

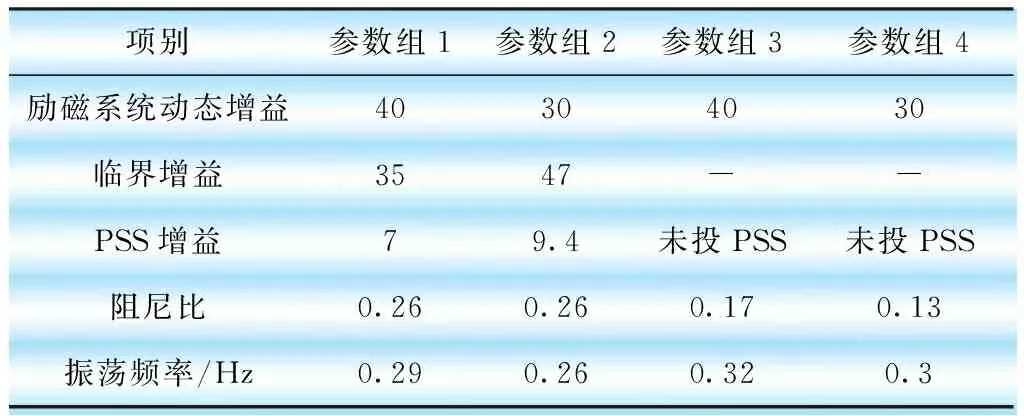
表6 不同动态增益的仿真数据及结果

5.2 PSS超前滞后环节二阶和三阶参数及仿真结果

PSS-2B 2组参数有补偿相频特性具体数据如图5所示。可见其有补偿相频特性较接近，在0.1～2 Hz范围内，三阶参数比二阶参数多滞后约10°，相位补偿均可以满足要求。在 0.1～2 Hz频段内，三阶的增益较优化前有较大提高，而高频段的最高增益反而更低。二阶和三阶参数仿真结果见表7。

通过对三阶参数和二阶参数对比仿真试验，PSS的临界增益由35变为45，阻尼比由0.26提高至0.3。通过上述仿真结果表明，可以通过适当调整PSS三阶参数，提高系统阻尼。二阶和三阶参数2%电压阶跃响应曲线如图6所示。

表7 二阶和三阶参数仿真结果

6 结束语

对于此600 MW机组接入当前电网结构，首先分析机组低频振荡的原因。为完成机组满负荷运行24 h要求，提出解决方案：继续提高现有PSS的增益，并观察PSS提高增益的情况下机组振荡模式和振荡频率；进行PSS超前滞后环节第三阶整定，能够在一定程度上提高PSS的临界增益，增加系统阻尼，提高输电负荷；暂不采用改变励磁系统动态增益提高PSS增益的方法。负荷、机组区域均衡发展，加强电网网架结构才是此项目解决低频振荡的最终方案。