基于拉格朗日方程的Delta机器人动力学分析

孙志伟，李亚洲※，武志华

（1.山东外事职业大学，济南 264500；2.山东博尔特电梯有限公司，山东德州 253400）

0 引言

机器人动力学分析描述了机器人关节力矩与机器人关节位置、速度、加速度之间的关系。动力学分析包含正向动力学分析与逆向动力学分析两类。正向动力学分析指已知关节驱动力，求解各相应部分瞬时运动，多应用于机器人运动仿真；逆向动力学分析指已知机器人关节的位移、速度和加速度，求相应的关节力矩矢量，是实时控制的需要[1]。常用的动力学分析方法有虚功原理法、牛顿—欧拉法、拉格朗日法等[2-10]。虚功原理的思想最早来源于欧洲的伯努利家族，后来在拉格朗日的《分析力学》一书中得到体现。虚功原理又叫虚位移原理，指的是外力在虚位移上做的功等于内力在虚位移上做的功。当系统势能不唯一时，依据最小势能原理，在平衡条件下总势能最小，所以其变分形式为0，可以据此条件联立方程。当用虚功原理处理力学问题的时候，实际上就是在进行动能为0时的E-L方程的推导，因此其推导过程较为复杂，而且虚功原理仅仅可以处理静力学问题，所以应用范围较窄。牛顿-欧拉方程针对刚体的平移和旋转问题，将两个关于刚体的运动方程组合在一起。一般情况下，牛顿-欧拉方程使用矩阵或向量进行运算。从本质上来讲，牛顿-欧拉方程描述了物体重心的运动与物体所受力或力矩之间的关系。牛顿-欧拉法通过平衡方程来求解问题，思路清晰，方法简单，不失为一种高效的动力学建模方法。但该种方法需要对机器人每一连杆分别建模，加之并联机器人结构复杂，所以计算量巨大，求解困难，运算效率低下，难以保证实时性。拉格朗日方法的理论基础是能量守恒原理，通常分别求取系统动能和势能，然后建立拉格朗日函数。使用拉格朗日法求解系统动力学，优越性体现在以下几方面：（1）求解过程中，避免了对系统速度和加速度的求解，因此计算量小、运算简单；（2）能满足实时控制的需求；（3）以矩阵的形式表示动力学模型，便于对系统进行动力学控制。

本文使用矢量法建立了并联机器人运动模型，分析了系统进给与连杆夹角、动平台空间位置之间的关系，获得了运动学方程。基于拉格朗日方程，建立了系统动力学模型，分析了系统进给量、连杆夹角对系统受力的影响。

1 并联机器人运动学分析

研究所用机器人如图1所示，顶端静平台固定于支架上，3条直线导轨端接于静平台，呈对称分布。连杆通过滑块连接直线导轨与动平台，端接于同一滑块的两根连杆互相平行，动平台与静平台均呈等边三角形。

图1 Delta机器人结构模型图

图2 Delta机器人空间直角坐标系

建立如图2所示的空间直角坐标系，坐标系原点O为静平台所在的等边三角形的中心，也即是直线导轨在静平台投影的交点。直线导轨上端点与静平台交于点PA、PB、PC。O-PA所在直线为坐标系X轴，且X轴正方向为由O点指向PA点。将X轴沿逆时针方向旋转90h为坐标系Y轴。Z轴正方向由O点出发，竖直向上。坐标原点O 到静平台端点PA、PB、PC的距离R=615 mm，直线导轨Lr=740 mm，连杆长度Lc=600 mm，动平台中心O′到动平台边沿的垂直距离r=58 mm，A导轨在静平台的直线投影与X轴重合，B导轨在静平台的直线投影与Y轴正方向夹角θ1=30°，B 导轨在静平台的直线投影与X 轴负方向夹角θ2=60°，C 导轨在静平台的直线投影与X 轴负方向的夹角θ3=60°，C 导轨在静平台的直线投影与Y 轴负方向的夹角θ4=30°，各直线导轨与静平台的夹角均为α=45°。连杆与各直线导轨分别交于点A、B、C。

假定原点的空间位置坐标为O=[0 0 0 1]T，通过齐次变换中的位置平移方法求得连杆与导轨交点A、B、C的坐标：

式（1）～（3）中：i1、i2、i3分别为附着于导轨A、B、C 上的滑块与导轨上端点之间的距离，也即代表伺服电机的进给量。

由于动平台空间位置是未知的，在此用未知量x、y、z表示动平台中心点的坐标，所以，以齐次坐标形式表示的动平台空间位置为：O′=[xy z1]T。使用平移的方法表示出各连杆与动平台交点A′、B′、C′的坐标：

以连杆长度为定值，即|AA′ |=Lc， |BB′ |=Lc， |CC′ |=Lc联立方程：

式（7）给出了电机进给量i1、i2、i3与动平台空间位置x、y、z之间的关系，即给定了这两组量中的任意一组，可以求解出另一组。

2 运动学验证

设定动平台空间位置，由式（7）求解电机进给量，借助机器人完成运动进给，将动平台实际位置与设定位置做对比，结果如表1所示。

表1 数据采样及误差

空间位置关系如图3 所示。考虑到测量的不准确性，系统误差在可接受范围之内。3台伺服电机在相同位置同时以相同速度做匀速直线运动，动平台运动轨迹如图4所示。此运动轨迹与实际运行轨迹相一致。

图3 空间位置关系折线图

图4 动平台运动轨迹

空间中，2 条已知的直线，可以求出2 条直线的夹角。以连杆AA′为例，假定电机进给量已知，由式（7）可知，连杆的2 个端点A、A′也确定，所以直线AA′的空间位置方程是确定的，可以分别求出连杆与坐标系各坐标轴的夹角：

式中：xA′为点 A′的 x 坐标，yA′为点 A′的 y 坐标，zA′为点 A′的 z 坐标，θax为连杆 AA′与 x 轴的夹角。

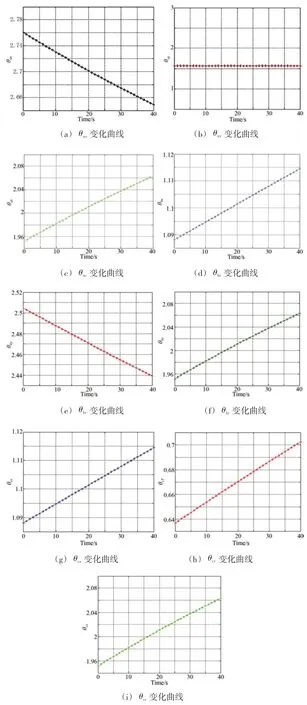
由式（8）同理可得连杆AA′与y 轴的夹角θay，连杆AA′与 z 轴的夹角θaz；点 B′的 x 坐标xB′，点 B′的 y 坐标yB′， 点B′的z 坐标zB′；连杆BB′与 x 轴的夹角θbx，连杆 BB′与y 轴的夹角θby，连杆BB′与z轴的夹角θbz；点C′的x坐标xC′， 点C′的 y 坐标yC′，点 C′的 z 坐标zC′；连杆 CC′与 x 轴的夹角θcx，连杆CC′与y轴的夹角θcy，连杆CC′与z轴的夹角θcz。在匀速直线运动条件下，各轴夹角随时间变化曲线如图5所示。

3 系统动力学分析

3.1 系统动能求解

由于直线导轨A在静平台的投影与坐标系X轴相重合，在位置上具有特殊性，动力学分析过程中选取B 导轨作为研究对象。由式（2）得点B的坐标（xB, yB,zB）。

使用位置平移的方法，求得连杆BB′的中点OB坐标（OBx,OBy,OBz）。令l代表连杆长度的一半，即。

点OB的广义速度：

B为滑块在B 直线导轨上的速度；为连杆 BB′与X 轴方向所成夹角的角速度；为点OB在y 轴方向的广义速度；为连杆BB′与y 轴方向所成夹角的角速度；为点OB在z 轴方向的广义速度；为连杆BB′与z轴方向所成夹角的角速度。

点OB的动能：

式中：EKB为连杆中点OB的动能；m为连杆的质量。

3.2 系统势能求解

以静平台所在位置作为零势能点，电机进给i2时的系统势能表述为：

式中：EPB为连杆中点OB的势能；Lr为直线导轨的长度。

3.3 建立拉格朗日函数

由式（12）～（13）可知，系统拉格朗日方程可以表述为：

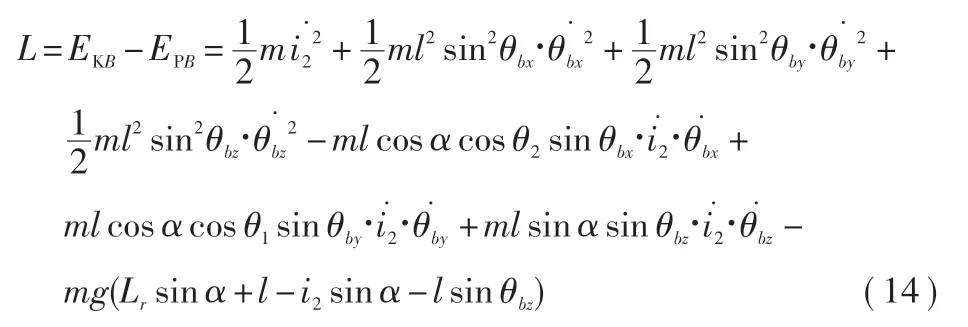
式中：L为系统拉格朗日函数。

3.4 建立动力学方程

电机进给在点OB产生的力矩：

式中：τ2为由于电机进给而在点OB产生的力矩；为电机进给加速度；为角θbx的角加速度；为θby的角加速度；为角θbz的角加速度。

同理可得因θbx角度变化而在点OB产生的力矩τbx，因θby角度变化而在点OB产生的力矩τby，因θbz角度变化而在点OB产生的力矩τbz。

同理可以求得各因素对连杆A和连杆C力矩产生的影响。

在匀速直线运动下，电机进给及各夹角对连杆力矩的影响如图6所示。

图6 中，τAi1为A 轴电机进给量对A 轴力矩产生的影响，τBi2为B 轴电机进给量对B 轴力矩产生的影响,τCi3为B 轴电机进给量对B轴力矩产生的影响。τAx、τAy、τAz、τBx、τBy、τBz、τCx、τCy、τCz分别为动平台空间位置坐标 （x，y，z）对各轴力矩产生的影响。

图6 各因素对力矩的影响

4 结束语

通过齐次坐标变换的方法搭建了运动学方程，建立了电机进给与空间坐标之间的对应关系，在此基础上求取了机器人连杆与坐标轴夹角的大小。使用基于拉格朗日方程的方法，建立了机器人动力学方程，具体步骤为：（1）求解系统广义速度；（2）求解系统势能；（3）建立拉格朗日方程；（4）对拉格朗日方程求偏导，建立动力学方程，分析各变量对系统力矩的影响。