基于多核聚类算法和用户兴趣模型的图像搜索方法

（重庆第二师范学院继续教育学院，重庆400067）

引言

随着信息技术的发展日新月异，海量图像信息的检索应用越来越广泛。自90年代初以来，个性化图像搜索一直是一个活跃的研究课题。近年来，在图像搜索与跟踪、特征提取机制以及相关的机器学习技术方面取得了一些进展。图像搜素已经引起了图像分析与处理、计算机视觉、心理学和安全等领域研究人员的关注。

人们通常利用搜索引擎来查询目标信息，但现有搜索引擎有两个明显缺陷[1]：（1）简化了图片搜索，仅仅进行文本检索，而未充分考虑图像语义间的相似性[2]；（2）在检索关键词的时候，所有相关的图像都被下载到索引库中，按照一定的排序规则反馈给用户[3]。也就是说，现有搜索引擎并不考虑个人兴趣喜好，针对同一个检索词的操作，无法根据用户的主观意愿进行相应的个性化搜索结果[4]。比较好的解决办法就是反馈。文献[5]将最小二乘法支持向量机 (Least Squares Support Vector Machines，LSSVM)引入到检索系统中，但需要用户标记正负样本，比较繁琐，而且没有解决正例样本较少的问题。针对以上问题，文中提出了一种新的图像搜索算法，根据用户的搜索指标，在对图像进行基于多核聚类的基础上，使用最小二乘支持向量机来建立用户兴趣模型，并将搜索结果呈现出来返回给用户。

1 几种聚类算法的比较

目前，常见的聚类算法包括K-means聚类算法、FCM算法以及多核聚类算法，下面分别详细介绍每种算法。

1.1 基于Hadoop的多维聚类算法K-means

K-means是一个十分简单的聚类算法，针对客户信息属性多维的特点，以及结合Hadoop的MapReduce算法的设计，以常规的K-means算法为基础，进行多维化的扩展。

常规的K-means算法包含以下几个步骤：

1）从图像对象中有针对性的选择个图像对象作为初始化聚类中心；

2）设定最小距离的初步临界值，通过计算每个图像对象与聚类中心的距离，进行初步的分类划分；

3）根据划分后分聚类中心，重新计算每个聚类的均值，这个均值是可以重新按照步骤2）进行变化的；

4）计算每一次划分后是否满足函数收敛，如果满足，则算法终止运行，如果条件不满足，则继续 2）、3）步骤。

K-means算法的迭代是通过Map函数及Reduce函数来实现的，Map函数默认的键值对为（Key,value）。为了便于计算，可以将图像数据按照属性导成文本形式。这里的key即当前文本的数据相对于起始点的位移，value则是对应的位移字符串。文本遍历后，通过value值计算对象与各个中心点的距离，从而找到距离最短的中心簇类。其设计的Map函数如下：

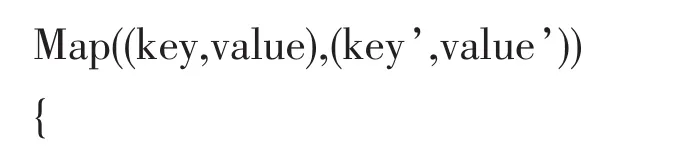
初始时解析value值得到初始值firstvalue；

距离中心聚类的最短距离定义为minvalue,初始化时为最大值；

Dex变量作为key’;

K定义为初始聚类中心的个数；

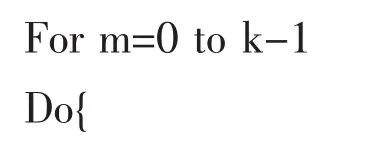
Dis=firstvalue;定义每一个对象与第m个聚类中心的距离；

Key’=index;每一次map函数执行之后将index赋值给 key’;

Value’=dis;将 dis作为 value’的值；

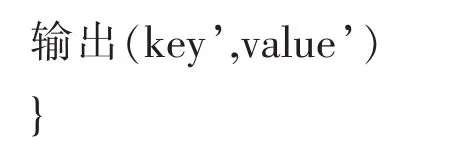
Reduce函数的输入来源Map之后的分类合并，即(key,V);这里的key是合并后聚类的下标，V是同一聚类的对象值即Map函数得到的value’;通过对同一聚类的各个对象value’值得相加除以同一聚类的对象个数，即为新的聚类中心的值。伪代码如下：

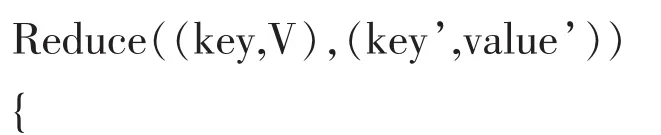
SUM[];初始化数组作为每一个聚类对象坐标的累加值。

NUM=0;初始化变量NUM，作为同聚类的对象个数；

While（V.hasNext()）//hasNext()用于判断是否有下一个同聚类对象；位移及对象个数；

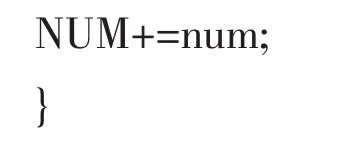
数组SUM[]的每一个值与NUM相除，得到各个聚簇中心新的坐标值；

即key变为 key’;

Value’的值即各个对象对应的坐标值；

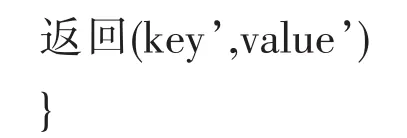
重复Map函数及Reduce，直到达到收敛条件。

1.2 模糊C-均值聚类算法FCM

FCM是比较常见的模糊聚类算法，其基本思想是通过计算隶属度表示每个数据点属于某个类的程度，并进行约束，从而实现数据分类。FCM把n个向量xi(i=1,2,…，n)分为c个模糊组，计算每组的聚类中心，使总体非相似性指标的价值函数达到最小，FCM算法最大的特点在于每个数据点隶属度的取值被规范在0和1之间，以更直观的确定其属于每组的程度。

首先，定义数据集中第个样本和第个聚类中心之间的误差平方：

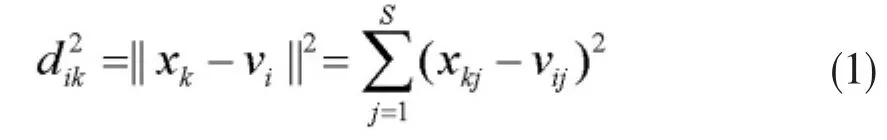
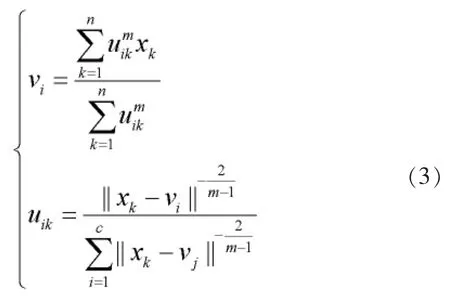
通过隶属度的平方加权来表示所有数据点与每个聚类中心的距离，进而得到每个聚类内的加权平方和目标函数：

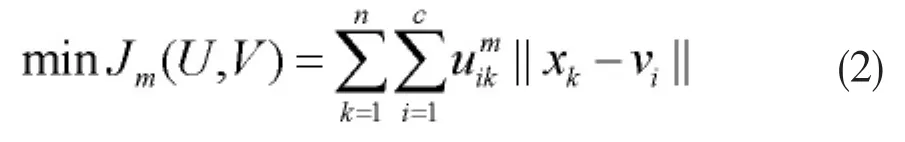
然后利用拉格朗日乘数法，可以得到算法的迭代公式：

1.3 多核聚类算法

多核聚类算法是指在传统的模糊聚类算法的基础上融入多核，引入动态核的权重，通过多核的方式可以有效地解决K-means算法、FCM算法的不足。对于选定的多核函数，根据权重的组合，可以满足不同的图像对核函数的偏好，最终得出最佳的匹配权重值。算法如下：

输出：wl,uij,vi及图像分类结果。

第一步：随机初始化第j个样本xi隶属于第i类的典型值为ti(0)，设置迭代次数为，最大迭代次数为tmax；令t的初始值为1；第t次迭代的隶属度矩阵为U(t)；第t次迭代的聚类中心为Vk(t)；

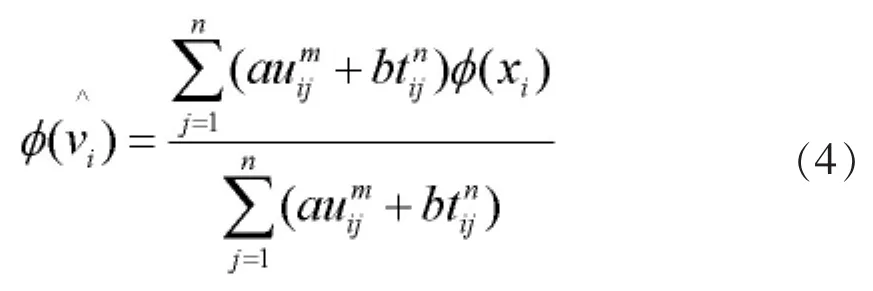
其中，uij为第j个样本隶属于第i类的隶属度值的大小，tij为第j个样本属于第i个类的可能性隶属度值，Φ为非线性映射函数，为原始空间的样本点。

第三步：利用下式获得第t次迭代的第j个样本隶属于第i类的隶属度值Vij(t)；

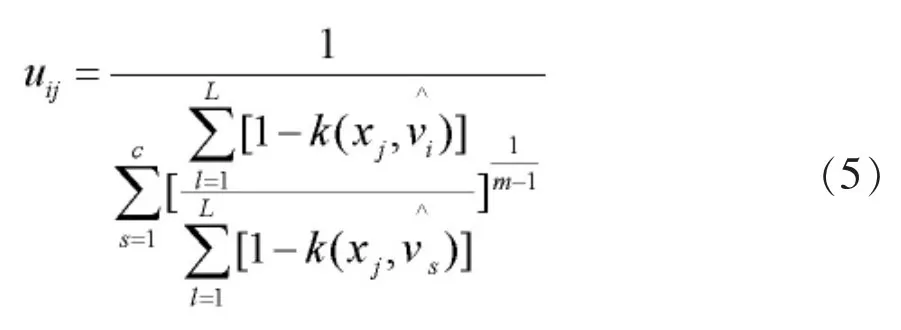
第四步：利用下式计算第t次迭代的第j个样本隶属于第类的典型值tij(t)；

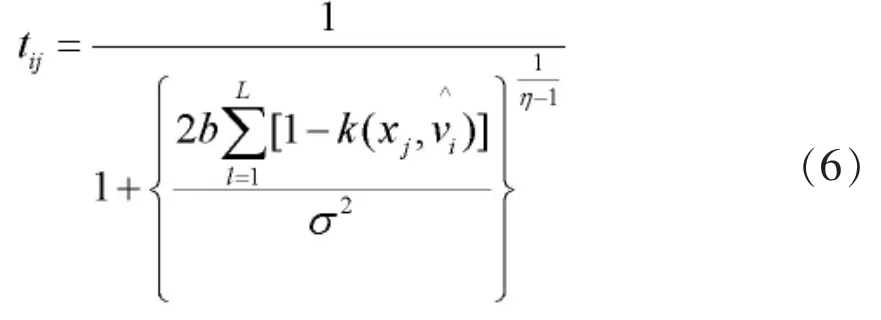
其中，σ2为协方差矩阵。

第五步：根据下式更新权重wl；

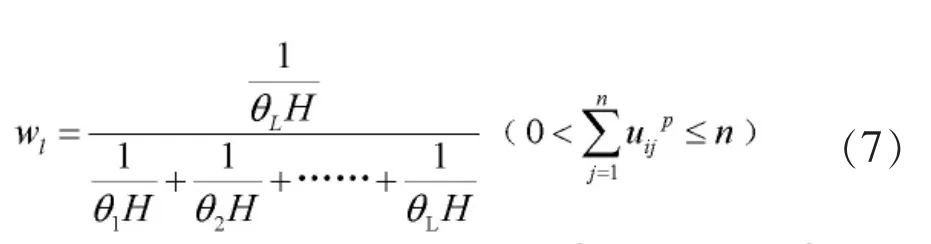
第七步：输出各个参数以及最终结果，结束。

1.4 比较结果

在K-means算法中，K需提前拟定，且K值的选定较难。在进行算法前，应根据初始聚类中心来确定一个初始划分，再对其进行优化。若初始值未选定合适，则可能得到无效的聚类结果。另外，K-means算法需要多次调整样本分类方式，并重新计算聚类中心，因此当图像数据较多时，会耗费较多的时间成本。

对于FCM算法，若一个类的样本容量很大，而其他类样本容量较小，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。同时，FCM算法只计算“最近的”邻居样本，使得某一类的样本数量很大，最终可能导致该类样本不能接近目标样本。此外，FCM算法的计算量也较大。

多核聚类算法能够规避其他算法对于核函数选择的不确定性。对于选取的多种核函数，凭借权重组合能够满足不同图像对于各种核函数的兴趣需求。综上以上算法的优缺点，本文选择多核聚类算法。

2 局部特征和全局特征的提取

提取图像中的关键特征是准确描述图像和提高图像搜索准确性的前提和基础。图像中包含的信息众多，不同用户根据自身关注点的不同对图像有不同的理解，即使对同一幅图像也会产生多种不同的特征描述。本文选取了局部颜色直方图[6]和全局纹理特征这两种底层的视觉特性进行计算。

在提取图像局部颜色特征部分，本文将图像分割成9个子块，分割方法如图1所示，而后将图像变换到HSV颜色空间中再进行相应的特征提取。

图1 将图像划分若干块

两幅图像x,y所对应的局部颜色直方图γ，Ψ间的视觉相似性使用核函数（8）计算，来描述不同图像视觉间的差异：

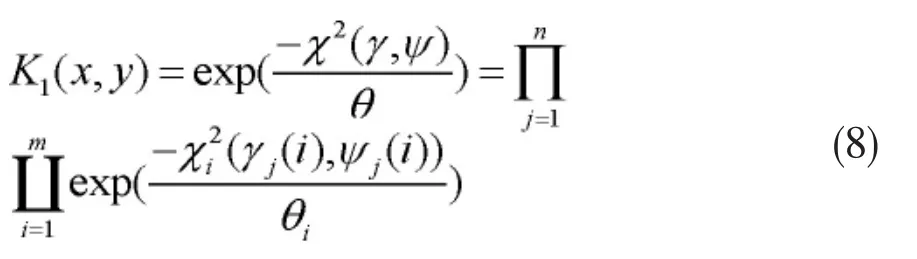
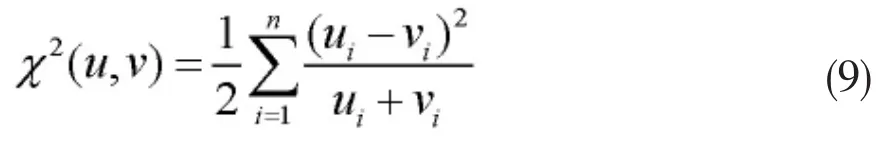
其中ui和vi是两副图像颜色直方图的分量。

本文使用频谱法进行纹理特征提取，采用2DGabor小波提取图像的纹理特征[7]，对于形状变化或者旋转都有较好的识别鲁棒性，如图2中所示。2DGabor小波变换采用图像卷积来表征：

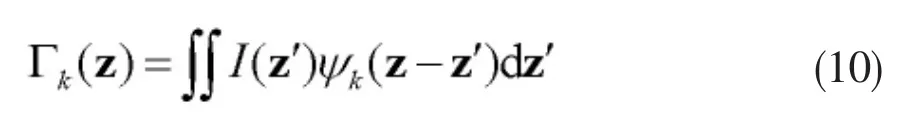
其中Gabor滤波器定义为：

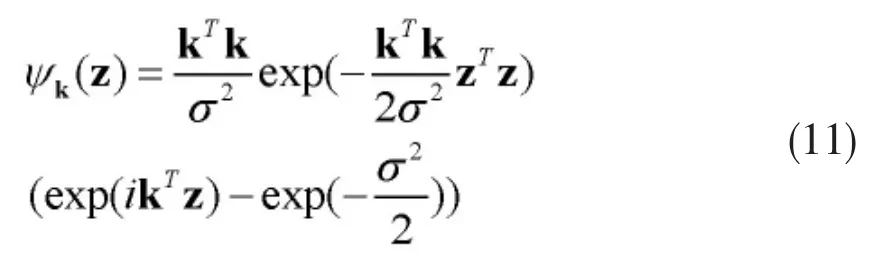
其中z=(x,y)，k代表波向量，满足以下关系：

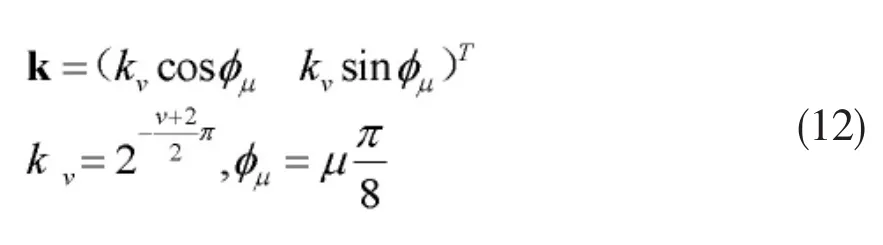
图2 Gabor特征提取示意图

使用公式（13）可以计算两幅图像的纹理相似性：

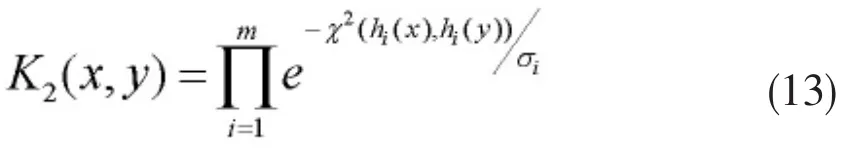
其中,σ=［σ1，…，σm］,表示 x2所有图像距离的平均值，x2均值的计算使用公式（9）。

3 建立模型

3.1 基于多核动态聚类工作流程

本文算法融合多核相似性与动态聚类，引入基于核函数的聚类方法。工作流程如下：

步骤一:设定参数聚类类别数C，以及允许误差Emax，确定初始化聚类中心Wi(k)， i=1，…，C;

步骤二:采用公式（8）和公式（13），将输入空间的特征向量映射到高维特征空间中；

步骤三:第i个子类的散度矩阵计算公式如下：

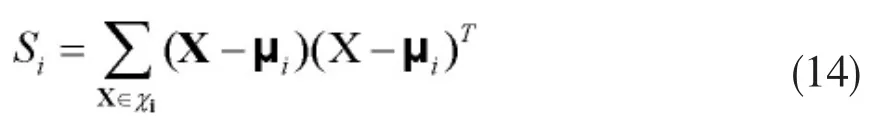
其中

由于使用散度矩阵的迹度量散度矩阵大小是一种有效的方法，它在最小化类内散度矩阵迹的同时，也最大化了类间散度矩阵迹，反映了聚集和分离程度。故求出trSi，并比较几个子类迹的大小，将迹最大的子类划分，按照相似度准则的标准进行二次聚类。直到实现预定的聚类数目，这时候得到新的聚类号[8]。

3.2 建立用户兴趣模型

3.2.1 最小二乘支持向量机模型

最小二乘支持向量机模型可以解决分类问题和函数估计问题，其数学模型的建立过程如下：

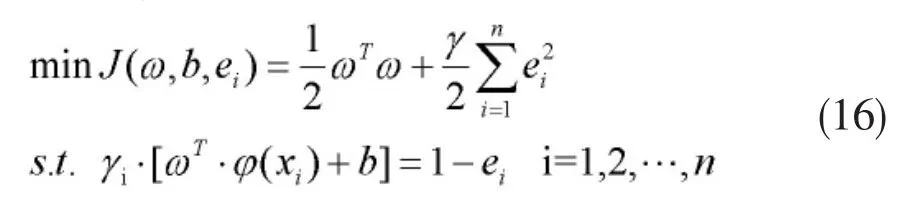
其中，ω为超平面方向向量，φ(xi)为映射函数，ei为xi的松弛系数，γ为边际系数。公式（16）的解可由对应的公式（17）所示的拉格朗日函数给出：

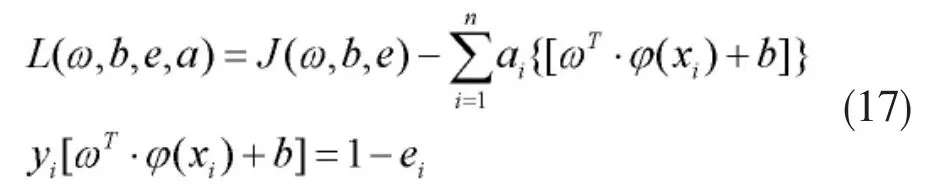
式中ai为拉格朗日乘子。根据公式（17）求得：

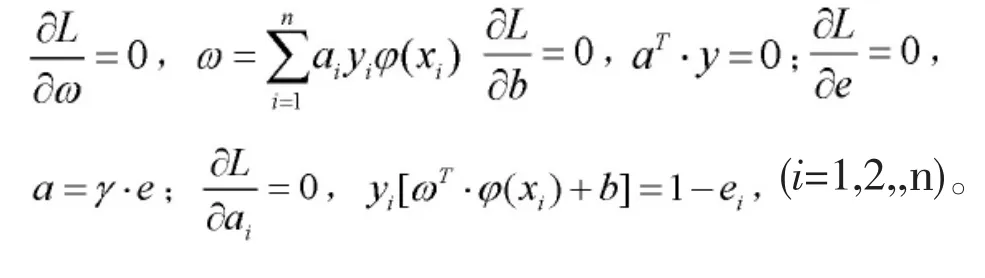
合并上式，可通过求解公式（18）的线性方程组得出ai和b的值。

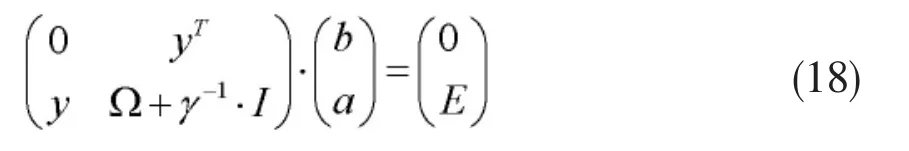
公式（18）中，Ω为n维对称方阵，I为n维单位阵，E为元素全为1的n维列向量，其元素为，，是核函数，因此，表示为Ω的元素（i行j列）。令可得到公式（18）的变形式：

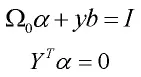
求解以上变形式，得到ai和b后，即可得LS-SVM 分类函数，见公式（19）：

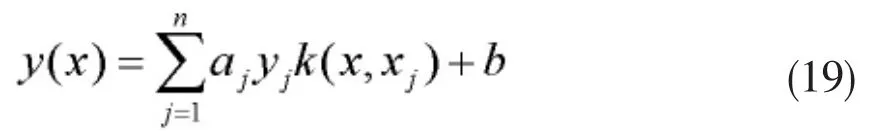
可以看出，计算LS-SVM分类模型时，无需考虑函数φ（·）的具体形式，只计算各个训练样本与待测样本之间的核函数k(xi,x)即可，待判模式向量的类别，由如下判别函数决定，见公式（20）：

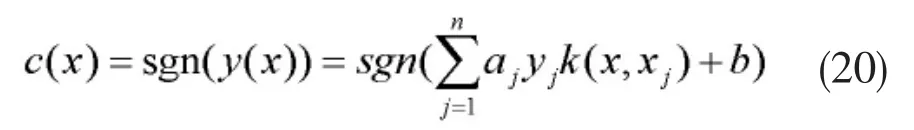
其中 sgn(·)为符号函数。若 y(x)≥0，则 x 被判为正类，否则x被判为负类。

3.2.2 建立用户兴趣模型流程

建立用户兴趣模型流程如下：

步骤一:线性组合公式（8）和公式（13），使用公式（15）计算每幅图像间的相似性，将得到相似度矩阵作为多核动态聚类算法的输入；

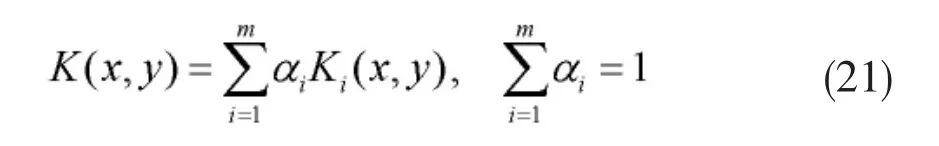
其中，ai≥0，m表示核函数的个数。

步骤二:通过多核动态聚类算法完成数据库样本图像的聚类；

步骤三:根据用户的搜索指标进行相关显示，如果实验结果不达标，则利用手动方式来人工选择感兴趣图片，然后，将聚类图像作为正例样本输送到最小二乘支持向量机网络中进行训练，从而确定分类面，构建个性化用户兴趣模型[9]。训练完成后，再一次查询样本库，将用户兴趣优先级高的实验结果进行优先选择，完成个性化搜索[10]。

图3实验结果与分析

实验中我们选取了Corel图像库进行测试，Corel图像库分成25个种类，每类含有100幅总共2500幅图像。选择的关键词，包括典型的大象、非洲、马、恐龙、花、家具6组。每组关键词选取60幅图像，这里选取360幅图像进行实验测试，图3为实验结果。实验中采用查全率与查准率进行系统评价，公式定义如下：

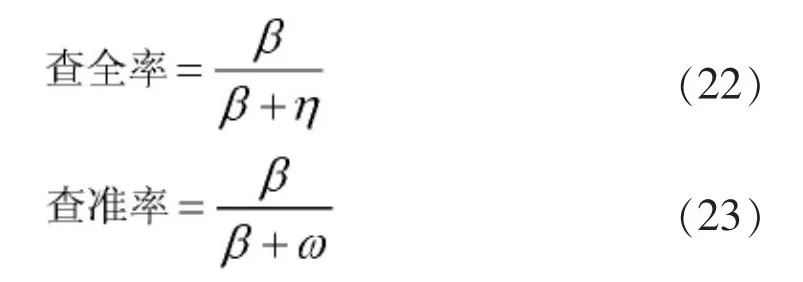
其中β表示检索出的相关图片，ω表示检索出来的不相关图片，η表示未检索出的相关图片实验结果如表1所示。

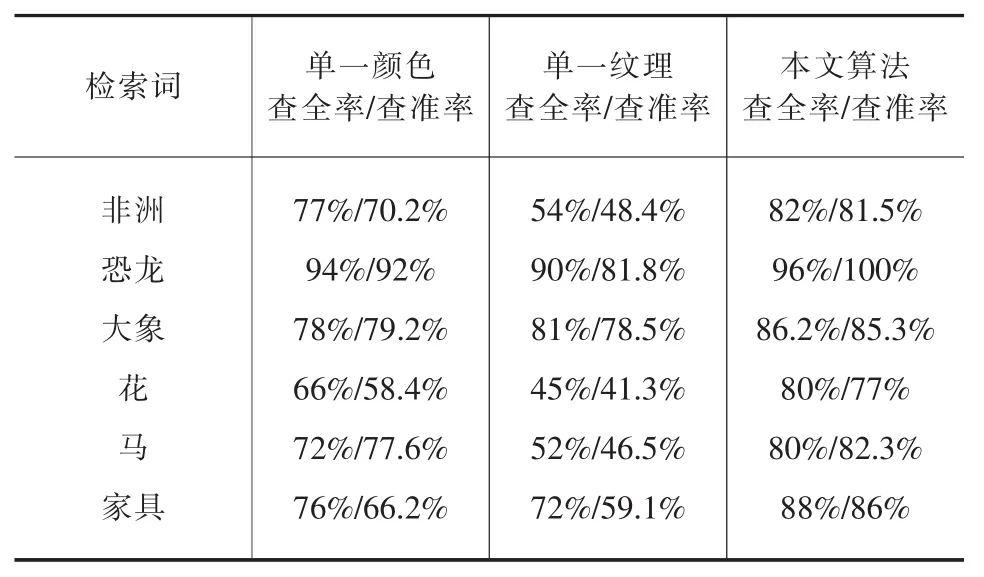
表1 传统检索方法与本文算法的比较

由表1所示，传统检索方法不能针对用户的需求建立兴趣模型，查询效果相对比较差，而本文提出的检索方法建立了用户兴趣模型，使得用户的主观需求参与检索，可以解决底层视觉特征与高层语义间的不匹配。通过对实验结果进行平均查全率和查准率的比较评估，本文提出的新方法比单一颜色特征的搜索算法分别提高了8.2%和11.42%，比单一纹理特征方法分别提高了19.7%和26.08%，改进效果明显。

4 结论

针对现有的搜索引擎算法不能完整地评价用户的查询目的同时代价较高的问题，本文提出的一种新的基于聚类和用户模型的搜索算法，该算法与传统的基于Hadoop的多维聚类算法K-means以及模糊C-均值聚类算法FCM相比，改进了传统最小二乘支持向量机需要过多用户参与的问题，将聚类结果作为正例样本送入最小二乘支持向量机网络进行训练，不断调整分类面，将该分类面重新应用于数据库的图像检索，通过实验可以看出，构建了用户模型的搜索方式可以更加准确全面地查找用户感兴趣的图片。