一种有效的异步电机参数辨识方法及运用

牛 莹，路 建，尹小龙

(西安中车永电捷通电气有限公司，西安 710018)

0 引 言

随着设备成本的上升以及空间的限制，无速度传感器控制逐渐取代速度传感器，而无速度传感器估算的方法又对电机参数有着较大的依赖性。电机的参数并不是固定不变的，如电机的电阻值和转子时间常数随温度与频率的变化而变化[1-2]。因此，在实现无速度传感器控制算法前就要对电机的这些基本参数与非基本参数进行计算，得到较为准确的电机参数的初始值[3-6]。传统的空载实验和堵转实验都需要大型的测量设备，测量极其不方便，而且当温度发生变化时，这种测量方式就不适合了。需要采用更加简单且有效的测量方法，即本文采用的在线辨识和离线辨识两种方法。选用TMS320F28377作为控制芯片，对电机的参数进行准确计算。TMS320F28377是双核处理器，CPU1主要对参数计算时的逻辑进行处理，CPU2主要完成对电机参数静止以及运行时的计算。仿真分析和实验验证了本文所提理论分析的正确性和准确性。

1 参数离线辨识

对于系统静止时候的初始值，需要采用离线参数辨识的方法，离线参数辨识就是给异步电机通入直流电和交流电进行参数自识别计算。定子电阻的初始值可以通过直流实验得到，转子电阻初始值和漏感初始值可以通过单相交流实验得到，定转子互感的初始值可以通过三相交流空载实验得到[7]。

离线参数辨识需要依赖电机的数学模型，将电机转子侧的电阻和电感值折算到电机的定子侧[8]。而电机定子电阻参数的初始值计算比较简单，其模型结构图如图1所示。将异步电机的AB两相通入直流电，回路中的电感相当于短路，回路中只有电机的定子电阻，回路中电阻的计算公式为式(1)，同样将BC、CA两相通入直流电，便会得到相同的计算公式，整理后可以得到定子电阻的计算公式，如式(2)。

(1)

(2)

传统的转子电阻、定子漏感和转子漏感的测量方法是对电机进行堵转实验，而本文采用给电机通入单相交流电的方法。电机通入交流的单相激励信号后是不会转动的，相当于堵转实验。在实际应用中，定子漏感与转子漏感的差值是很小的，其值远小于电机的互感值，故一般将励磁支路视为开路。如图2所示，通过电机的有功功率计算和无功功率计算可得转子电阻和定转子的漏感，如式(3)和式(4)，其中θ为功率因数角。

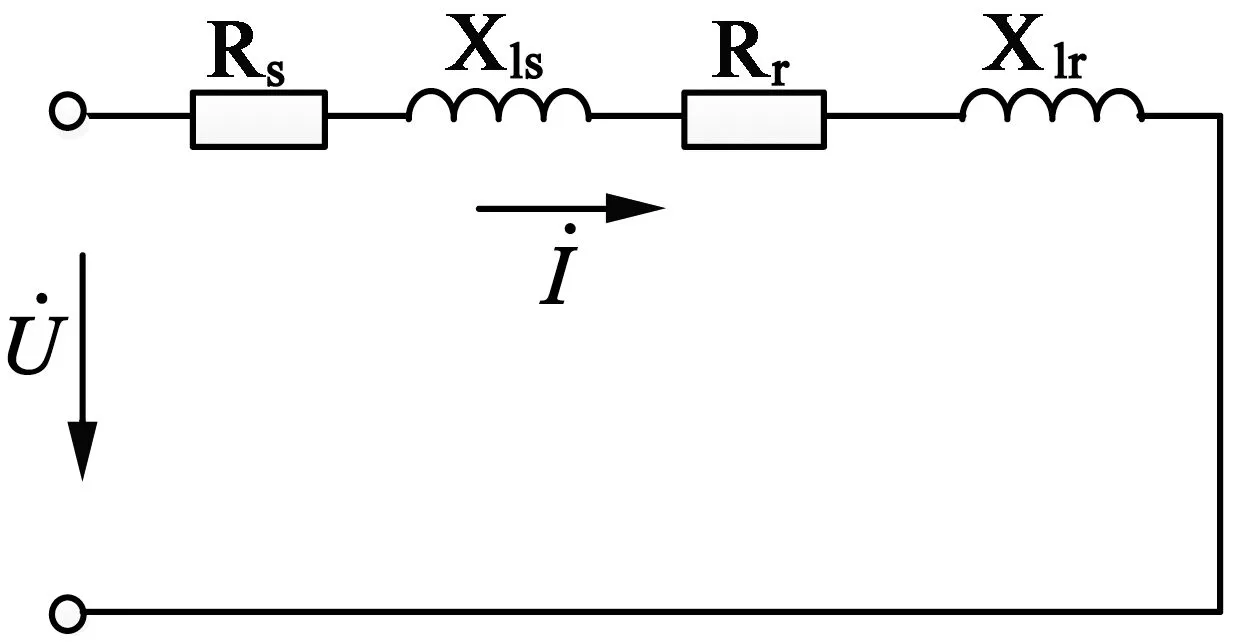
图2 单相交流等效电路图

(3)

(4)

通入三相交流电测量电机的互感。当电机转到nN时，转差率s变为0。此时电机转子侧等效为开路，定转子互感值变为式(6)所示。

(5)

(6)

式(3)～式(6)中都含有θ，因此需要准确计算出θ。本文采用相关函数的算法，相关函数在计算的时候包含自相关函数和互相关函数[1]：

(7)

(8)

式中：x(t)与y(t)是两个不同的随机信号；x(t+τ)与y(t+τ)是x(t)与y(t)延迟时间τ后的信号。离线参数辨识时，定子侧输入电压信号u(t)和测得的电流信号i(t)的计算公式如下：

(9)

式中：Nu(t)、Ni(t)为噪声干扰信号。

根据正弦函数的和差角公式，对式(9)进行简化，可得到下式：

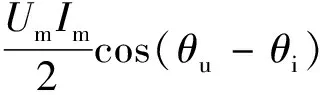
(10)

对于信号u(t)和i(t)，当τ=0时，自相关函数：

(11)

化简后：

(12)

2 参数在线辨识

电机在运行时，机身温度、转速、磁饱和度等都会发生变化，而这些因素都会影响电机电阻的阻值，其中机身的温度对电机电阻变化的影响最大。定子阻值与温度的变化是非线性的关系，最大变化范围是2倍的关系。在模型参考自适应的计算中，电阻的改变会改变电压模型中的转子磁链，其中转子磁链的计算公式：

(13)

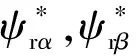
通过Popov超稳定性理论的分析，得到定子电阻辨识的自适应律如下：

(14)

式中：kp为比例系数；ki为积分系数。

由Tr=Lr/Rr知，当转子电阻Rr发生变化时，转子时间常数也随之发生改变，将会导致转子磁场定向计算的不准确，将1/Tr的自适应律改写成比例积分的形式：

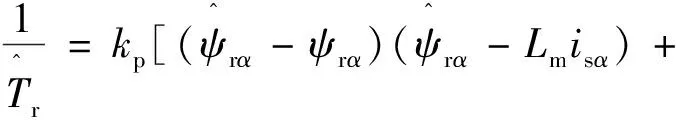
(15)

将上式转换到s域：

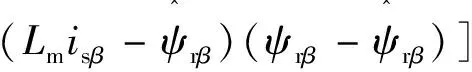
(16)

3 仿真与分析

在MATLAB/Simulink中搭建仿真模型，通过仿真与分析验证电机参数辨识的正确性和准确性。因为仿真模型为理想模型，不能模拟特殊激励的工况，所以在仿真中只进行参数在线辨识。按照定子电阻在线辨识构造出定子电阻自适应律模块仿真图，如图3所示。

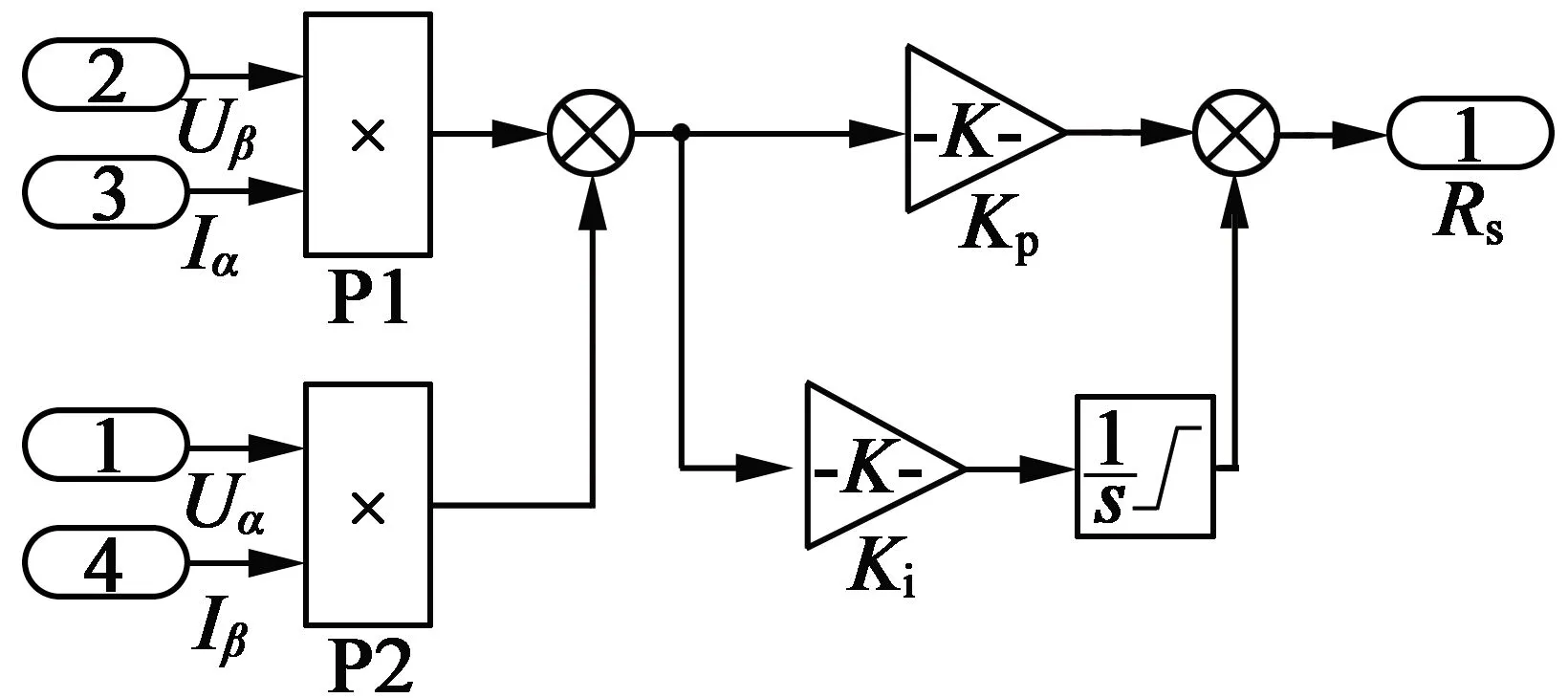
图3 自适应律模块仿真图

电机的电阻会受电机的温度和机身的老化影响，由于这在仿真中难以体现，所以采用改变仿真中电机电阻阻值的参数来模拟电机的电阻值随时间和温度的变化。电阻在线辨识结果如图4所示。

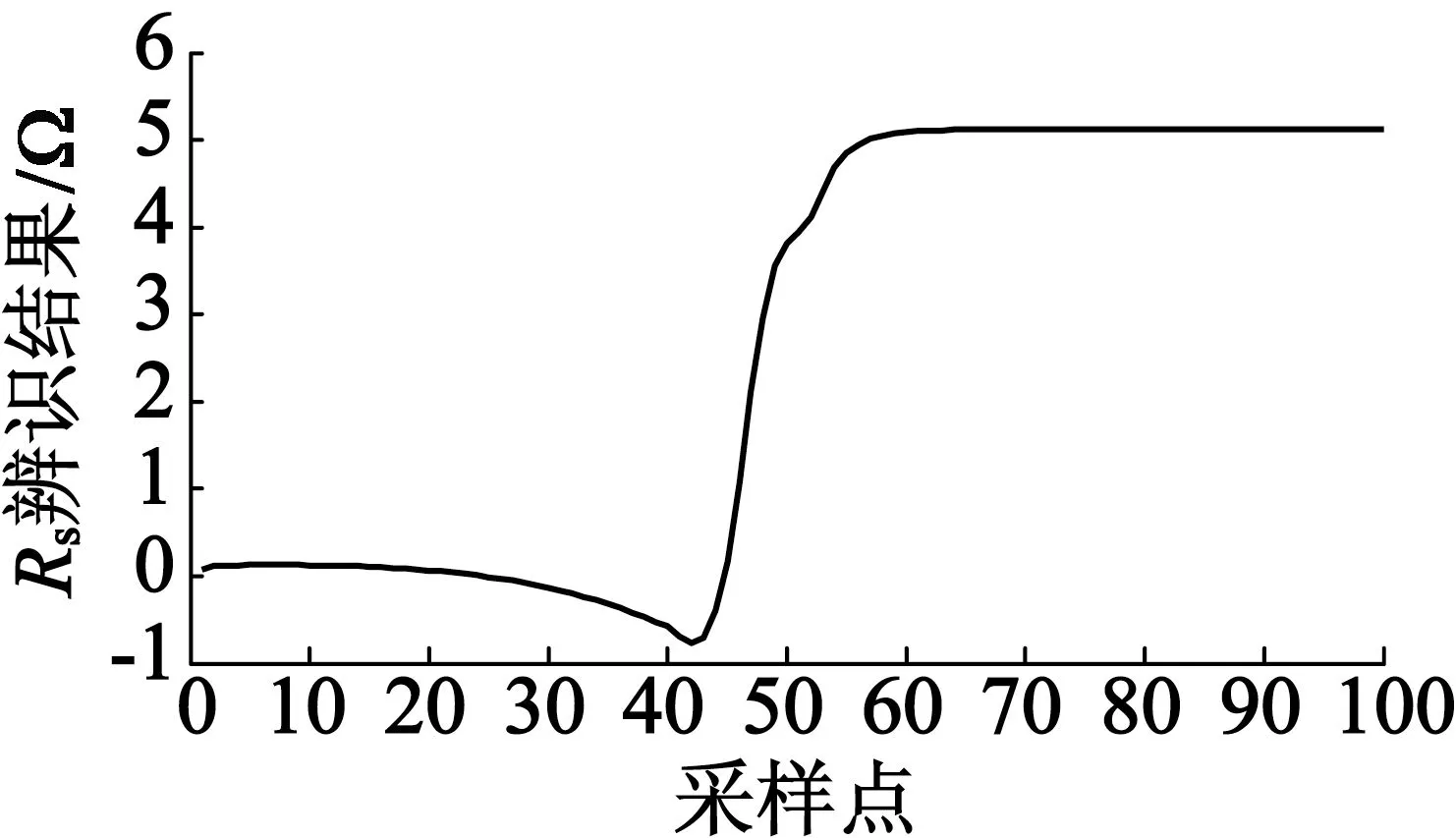
图4 Rs在线辨识结果

转子时间常数的仿真模块按照式(16)搭建，如图5所示，忽略外界其他因素对转子电阻影响的情况下，通过在线辨识仿真分析转子时间常数的变化趋势。在仿真模块中用的转子电阻的阻值为5.06 Ω，转子电感值为0.423 H，计算可得11.958 s。从图6能够看出，收敛速度非常快，在线辨识响应非常好。

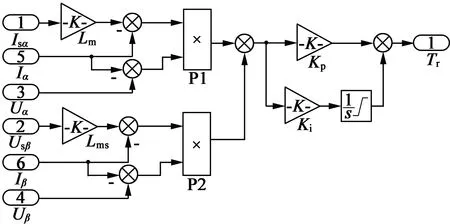
图5 1/Tr自适应律模块仿真图

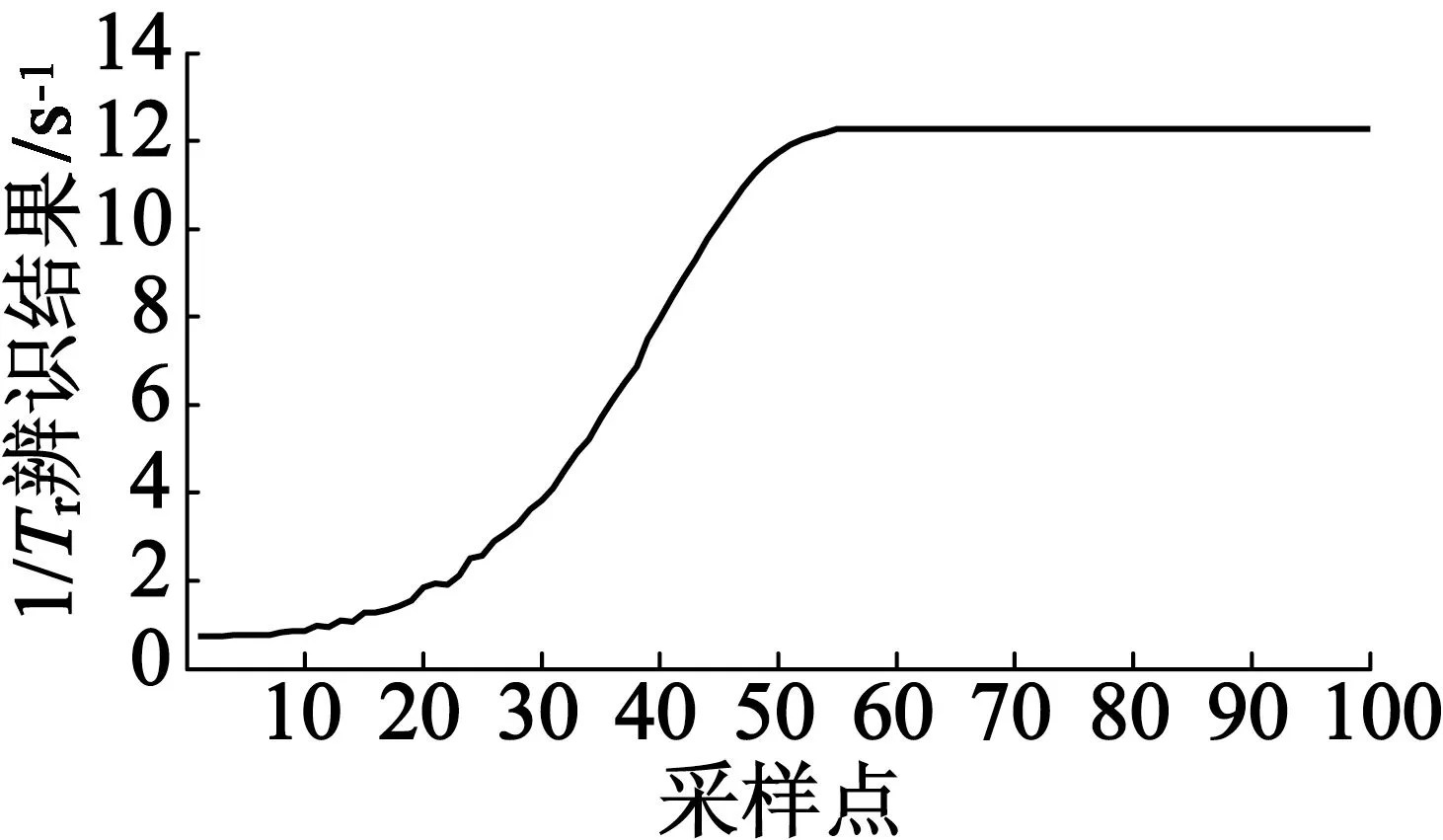
图6 在线辨识结果

对图4和图6的辨识结果进行分析可知，定子电阻和转子时间常数都可以较快地达到收敛并且保持稳定的辨识值。

4 实验验证

本文所采用的实验电机为三相异步电机，电机参数与仿真保持一致，电机参数如表1所示。

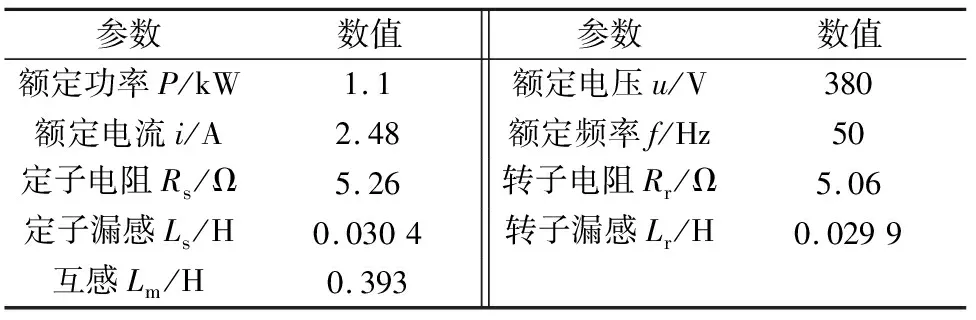
表1 异步电机参数

(1)单相交流实验

给三相电机中的B相通入单相交流电，通过采样电路得到单相交流电压和单相交流电流波形，如图7所示。从图7中可以看出，电压波形的相位超前电流波形。再从CCS6.2中STATEFLOW窗口读取5组不同的数值，然后求平均值，便可得到转子电阻值和漏感值，如表2所示。

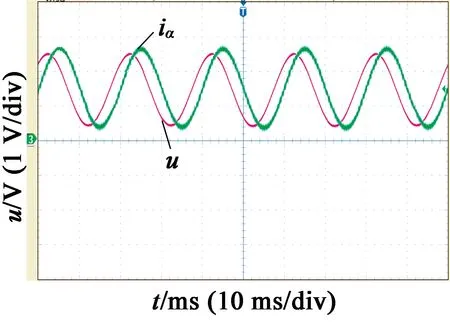
图7 单相交流实验波形

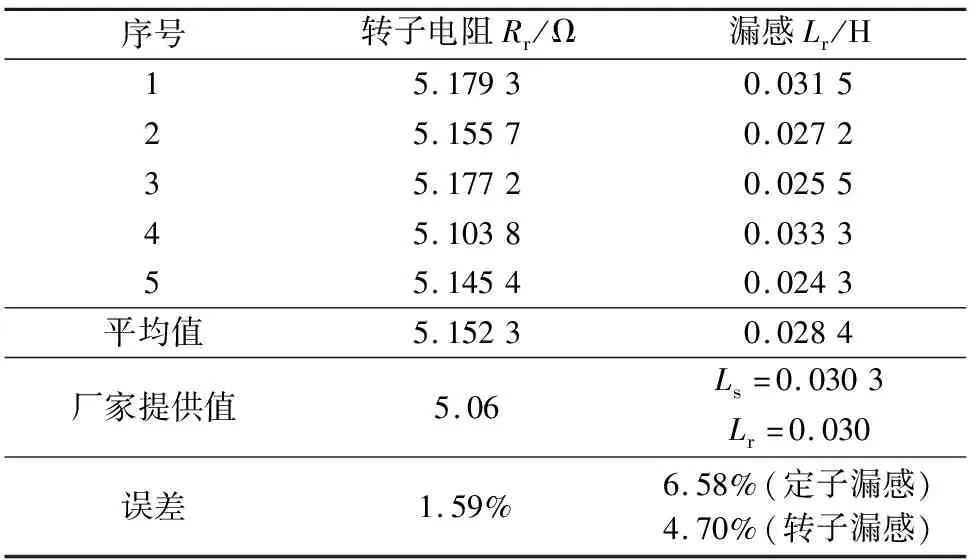
表2 转子电阻及漏感离线辨识数据

(2)三相空载实验

通入三相交流电，使电机空载且运转在额定转速下，测得B相的相电压波形和相电流波形，如图8所示，与通入单相电是一样的，相电压的相位超前相电流。从CCS6.2中的STATEFLOW窗口中读取5组不同数值，通过定转子的计算公式便可以得到程序中的定转子互感值，然后选取平均值，如表3所示。

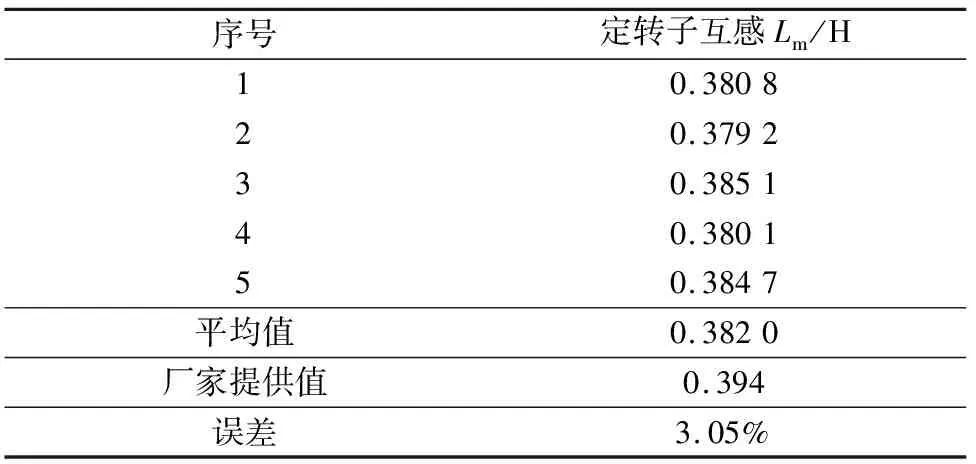
表3 互感离线辨识数据

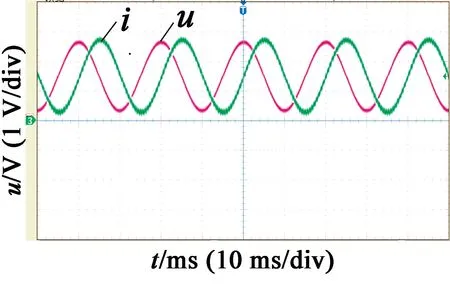
图8 三相空载实验波形

从表格中的实验数据可以看出，本文设计的离线辨识的方法可以准确地测出定子电阻、转子电阻、定转子互感、漏感等，而辨识过程中产生误差可能是干扰信号的影响和采样精度等导致的。

5 结 语

本文通过离线辨识与在线辨识相结合的方法可以准确地计算电机的基本参数与非基本参数，离线辨识主要包括直流实验、单相交流实验和三相交流空载实验，目的是为获得电机定子和转子电阻的初始值、漏感的初始值和互感的初始值。由于电阻受温度和磁场变化等因素影响，所以需要在线辨识，获得更准确的电阻值和转子时间常数。在线辨识通过Popov超稳定性理论得到自适应律，由仿真波形看出，辨识过程的收敛速度比较快，且稳定以后误差比较小。实验结果验证本文设计的参数辨识具有辨识误差小、准确度高的优点，可以满足大部分无速度传感器的速度辨识的场合，而且计算简单，具有较好的应用性。