基于自抗扰反步法的高空飞行器动力电机控制率设计

娄 鹏，宋剑桥，殷佩舞，孙耀程

(中国电子科技集团公司第二十一研究所，上海 200233)

0 引 言

对于高空飞行器动力电机动力系统，螺旋桨负载尺寸大、转动惯量大，需求的动力驱动电机力矩大，转速相对较低，为了安全高效和较好的飞行品质，螺旋桨的动力驱动电机采用永磁同步电机系统，控制方式采用在0到360°电周期内磁场定向旋转的控制策略(以下简称FOC)，这种旋转磁场定向的模型方法的应用大大提高了控制品质和电机性能[1]，FOC核心是转速环作为外环控制，励磁电流(id)和转矩(iq)电流的控制作为内环控制，有效地降低控制模型中各个参数之间的耦合问题[2]。

高空飞行器用螺旋桨动力系统驱动电机FOC(磁场矢量控制)模型中，多环控制的模型中存在多个输入的变量与相应输出结果的非线性特点，各参数间也存在强耦合的特性[3]。大型高空飞行器动力系统多安装于碳纤维杆组成的支架上，飞行器结构振动、遇大风等恶劣工况会导致系统工作情况复杂，使得电动机运行时内部参数都会存在急剧突变的情况,从而影响着高空飞行器动力电动机的实际控制性能。本文设计了基于自抗扰反步法的外环控制器，以实现对大尺寸螺旋桨负载动力电机转速的精确控制。

1 高空飞行器动力电机控制系统总体结构

图1中，ωe为动力电机的期望转速；ωfed为动力位置传感器反馈的螺旋桨(也是电机输出轴)当前转速；iq为动力电机的期望转矩电流；id=0为动力电机的期望励磁电流；idf,iqf分别为动力电机系统采集到的三相电流iA,iB,iC经过坐标变换后的交轴(q轴)和直轴(d轴)反馈电流；vd,vq分别为动力电机期望的交轴和直轴电压。在外环控制中，转速跟踪控制器根据当前转速与期望转速间的误差，解算出实现该转速跟踪的q轴电流。内环控制中，转矩稳定控制器将外环计算出的期望q轴电流作为输入，与当前q轴电流比较，计算出动力电机q轴电压输入量。同理，计算出d轴电压输入量。控制输入量控制电机本体做出相应的电流和转速改变，并将状态信息反馈给基本控制律，从而使电机控制系统成为闭环系统[4]。

图1 高空飞行器动力电机基本控制律结构框图

2 扩张状态观测器设计

扩展状态观测器的数学模型如下。

对于下列系统：

(1)

式中：x1,x2为系统状态变量；f[x1,x2,w(t),t]为未知时变非线性函数；w(t)为时变外界扰动；y为系统输出；u为控制输入。

在螺旋桨负载电机矢量控制模型建立的过程中，由于各种近似与简化处理，使获得的力学模型与螺旋桨负载的真实受力之间存在较多误差，而这些误差主要存在电机矢量控制模型中对电机电感、转子磁链等参数的简化[5]。同时，各种外部干扰比如阵风、扰流等也会对机体施加力的作用，无论是矢量控制模型误差还是外界扰动造成的影响，统称为“总的扰动”。如果这些扰动力造成的加速度误差能够被估计出，那么就可以在反步控制法中将其补偿。而扩张状态观测器的设计目的就在于实现对转速干扰的估计[6]。针对电机控制模型的扩张状态观测器可以设计为如下结构：

(2)

式中：V为电机转速；z1为V的观测量；z2为干扰转速的估计值；iqm为下面设计的控制器输出的电机转矩电流期望值；J为螺旋桨负载转动惯量；β01,β02为观测器的反馈增益；fal()为观测器的非线性非光滑反馈函数。

通过观测器，z1可以实现对当前速度V的跟踪，z2可以实现对干扰转速的准确估计。得到干扰转速的估计值z2后，将实现对外环控制器输出的电机转矩电流的补偿，从而使控制器具有抗干扰能力[6]。

3 反步控制法原理

反步控制法稳定性定理由俄国力学家Lyapunov提出，其定义如下。

对于如下系统：

(3)

设x=0为其一个平衡点，D⊂Rn为包含原点的定义域。建立数学模型函数V(x)，此函数可对变量x求一阶导数，V′(x)为连续函数，对状态空间Rn中所有状态点D满足以下条件：

V(0)=0，V(x)>0，在D-{0}内

则系统的原点平衡状态x=0为Lyapunov意义下稳定。

此外，如果V(x)满足以下条件：

V(0)=0，V(x)>0，在D-{0}内

则系统的原点平衡状态x=0为Lyapunov意义下的渐近稳定。

4 自抗扰反步控制器设计

根据反步控制法原理，针对高空螺旋桨负载动力电机模型，进行如下自抗扰反步控制器的设计。

第一步,对于外环转速调节系统，将V视为控制输入，转速误差ωe=ω-ωfed，其中，ωfed为电机当前转速，ω为电机期望转速。设计转矩电流Lyapunov函数：

(4)

其导数：

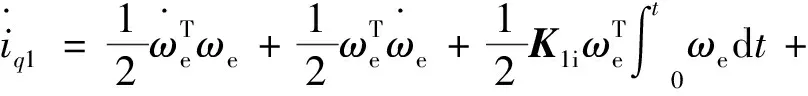
(5)

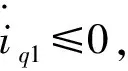
(6)

式中:V为虚拟输入速度；K1p,K1i为恒定的正定矩阵。从而使得：

(7)

第二步，对于内环电流调节系统，将iqm视为控制输入，定义虚拟输入误差为Ve=V-Vc。设计Lyapunov函数：

(8)

其导数：

(9)

(10)

式中：K2p，K2i为恒定的正定矩阵。从而使得：

(11)

经过上述步骤，得到控制输入iqm。

在以上控制律的设计中，首先通过扩张状态观测器对电机受到的干扰转速进行观测，并得到估计值z2，将z2用于对电机转动模型的修正，从而获得更加准确的模型。基于该模型进行反步控制法的设计，最终获得的控制输入iqm包含了对总的扰动的补偿，从而使控制律具备了抗干扰的能力，并且从理论上保证了外环控制律的渐近稳定性。

5 内环PID控制器设计

反步控制法基于级联系统逐级进行控制输入的计算，如果将反步法沿用至内环姿态控制，针对直升机系统，反步控制的级数将达到2级，而根据外环控制律的设计可知，在每一级都拥有6个控制参数(Kp,Ki)，因此整个控制律将拥有12个控制参数需要调节。而且反步控制法在每一级设计前，都需要对前一级获得虚拟控制输入求取一阶导数，若控制级数增加，对期望值的求导阶次也会增加，而高阶导数往往受到噪声污染，从而使控制效果变差，综合以上考虑，本文的内环姿态稳定控制器采用经典的PID控制方法设计，以减少控制律参数和期望值的求导阶数，从而减少噪声等因素对控制效果的影响[8]。

电机矢量控制模型电流环具有两个控制输入量，力矩电流iq和励磁电流id。通过这两个输入量控制电机输出转速和转矩。利用外环位置跟踪控制器获得期望力矩电流后，将其作为内环姿态稳定控制器的控制期望。根据电流采集得到iA,iB,iC进行坐标变换后进PI计算[9]。

内环姿态稳定控制律的具体算法如下：

(12)

式中：取idref=0，iqm由外环位置跟踪控制器得到；kpq，kiq，kpd，kid为内环控制律参数。

6 控制实现及实验验证

图2为引入自抗扰反步法控制系统结构框图，控制器系统主要包含主控逻辑电路和功率驱动电路。

图2 电机控制器系统结构框图

功能模块包含位置传感器角度检测、电流采样、自抗扰速度控制器、坐标变化、SVPWM模块、整流及逆变模块构成。按照图2的控制结构框图，研发针对高空动力电机驱动控制系统软件，程序流程图如图3所示。

图3 控制器程序流程图

研制实验样机如图4所示。高空螺旋桨尺寸7 m,质量33 kg，调速范围0～370 r/min，电机控制器输入电压270 V(DC)，电机额定转速370 r/min，电机额定转矩330 N·m。

图4 高空动力电机系统样机及起动测试

分别从零转速起动电机运行至500 r/min,电机控制器采集位置传感器数据，并通过内部计算得到实时转速数据并传输给上位机系统，得到负载起动和扰动转速波形如图5、图6所示。

图5 螺旋桨负载起动速度波形

图6 螺旋桨负载扰动速度波形

电机运行至转速稳定后，根据图5、图6中得到的转速波形数据，引入自抗扰反步法控制后，电机转速比常规PID控制波动更小，系统抗干扰能力增强。

7 结 语

本文首先分析了高空飞行器大功率螺旋桨负载动力推进电机转速的控制重点与难点，设计了基于自抗扰反步法的外环位置跟踪控制器，实现了自抗扰功能，同时保证了控制系统的稳定性。然后为简化基本控制律结构，使其能够投入实际使用，采用经典的PID算法进行了内环姿态稳定控制器的设计，内环电流控制器根据磁场矢量模型的特点，对励磁电流和转矩电流进行独立的控制器设计。最终通过内、外环组成的控制律实现了对动力电机的闭环控制，增强控制系统抗干扰能力。