基于蒙特卡罗法的感应电机转子槽数及转速辨识方法

李 良，宋文乐，张树亮，蒋 曦，王朝阳，赵俊蕾，李鹏宇

(1.国网河北省电力有限公司沧州供电分公司，河北 061001；2.华北电力大学 电气与电子工程学院，北京 102206)

0 引 言

笼型感应电机具有运行稳定、结构简单的特点，且广泛应用于社会生产中。当感应电机运行状态稳定时，其转子转速是一个非常重要的运行参数，可以利用转速数据计算电机负载率，也可以通过查表方式来评估电机的运行效率[1-2]。在实际工程中，很多现场环境不允许电机停止运转，在这种情况下不具备安装转矩转速传感器的条件，若能安装也会耗费大量人力物力。如果想得到电机转速近而评估出电机的运行效率，就有必要研究一种非侵入式的转子转速评估方法。目前，通常采用转子槽频率法进行转子转速辨识[3-4]。但由于笼型感应电机及其设计的多样性和商业机密等因素，对于从事现场评估的人员来说，如果通过拆卸转子获得转子槽数，工程量较大，同时也会影响正常生产，难度较大。因此，如何通过一种非侵入式方法准确获得转子槽数，成为工业现场电机系统能效评估面临的一个重要问题。

非侵入式电机系统参数与能效评估历来都是众多学者研究的对象，且已经取得了很多成果。文献[5]对变频异步电动机的非侵入式效率估计提出了一些考虑，重点讨论了不同谐波等效电路附加损耗的量化以及电压、电流谐波对其性能的影响,在分析现有的电机能效评估方法的基础上，提出了最新方法的推荐技术。文献[6]提出了一种可转换为自适应观测器形式的感应电机模型，在参数不变的情况下，建立转速和转子电阻自适应观测器，并对无传感器驱动系统进行了实验验证；文献[7]考虑了电机参数随运行工况实时变化的特点，提出了一种基于等效电路法的改进算法，并进行了实验验证；文献[8]则提出了一种基于滑模法和磁化电流估计的感应电机转速观测器并基于李亚普诺夫方法进行了稳定性分析；文献[9]利用修改后的粒子群优化方法对转子时间常数进行实时跟踪，并用实验验证了该方案的鲁棒性和有效性；文献[10]提出了两种不同的电机参数实时估计方法，包括基于磁链观测器的模型参考自适应系统和基于脉动磁链注入的方法，并通过实验评估了这两种方法的优缺点。

1)未知的转子槽数。根据理论分析可知，要想通过转子槽频率来获取电机转子转速，其转子槽数必须是已知量。但是在不清楚电机具体结构的情况下，定转子槽数其实是一个未知量，且很难在现场获取到，而上述文献均将转子槽数视为已知参数。所以即使对定子电流进行快速傅里叶分解后得到了某些特定频率，也无法准确获得转子槽谐波的频率。

2)定转子槽谐波混叠。某些特殊结构的电机，比如定子槽数和转子槽数相等或接近相等时，定子槽谐波和转子槽谐波在频谱上的分布十分接近，从而发生混叠现象，导致很难从频谱中把定子槽谐波和转子槽谐波准确分辨出来。

为了解决上述问题，本文在对转子转速在线辨识研究的基础上，结合蒙特卡罗法与电机运行中空载和额定负载两个特殊工况来辨识电机转子槽数，然后使用转子槽谐波法完成对电机转子转速的辨识，并根据转速评估电机的运行效率；并以5.5 kW电机为例进行实验验证。

1 基于转子槽谐波的转速辨识方法

在正常情况下，电机定子和转子未开槽时，定子绕组通入电流后所产生的气隙磁动势[4]：

(1)

式中：α为机械角；ω1为角频率；Fν为ν次谐波磁动势振幅；p为极对数；ν为谐波次数。

当电机定转子开槽以后，此时气隙磁导可表示：

(2)

式中：Λm，n为对应于m和n阶的磁导，其中m和n为整数，分别代表定子和转子槽产生的磁导谐波阶次；z1和z2分别为定转子槽数；ωr为转子角速度。

国际贸易法律复合人才作为重要的战略资源，直接影响我国“一带一路”倡议的实施效果。“一带一路”倡议的深入纵深推进，必然要依靠国际贸易法律实务高端人才的优质供给和有效供给。在当前全球化进一步加剧的新时期，我国要把握机遇，发展自我，就必须在国际竞争中占据先机，而人才正是我国在国际化发展进程中占据先机的重要武器。基于“一带一路”倡议视野，加强国际贸易法律复合人才法律英语教学，包含了对国际贸易人才国际视野、知识储备、专业水平、实践技能等总和义务素质能力的考量，成为我国“一带一路”倡议的关键助力。

进一步推导可得到开槽后的气隙磁密如下：

cos[(nz2±mz1±νp)α-(nz2ωr±ω1)t]

(3)

式中：u0为磁导率；Bν,m,n为对应于第ν次，第m和n阶的磁密值。

从上述公式可以看出，当电机定转子开槽以后，定子槽谐波在定子侧三相对称绕组中感应出基波电动势；转子槽谐波也会在定子侧三相对称绕组中感应出相应的电动势，此电动势在定子绕组上会产生对应频率的谐波电流，这种电流谐波就是转子槽谐波，频率可用式(4)表示：

fsh=f1z2(1-s)/p±f1

(4)

式中：s为转差率；f1为三相电源频率。

由式(4)可知，由转子槽频率可以计算出转差率，从而便可以计算出转子转速：

n=60(fsh±f1)/z2

(5)

由式(5)可知，只要知道了转子槽频率、三相电源频率和转子槽数，将其代入式(5)便可辨识出转子转速。转子槽频率可通过对定子电流快速傅里叶分解得到，三相电源频率一般为工频，但转子槽数是未知数，其计算方法将在下文详细论述。

2 现场转速辨识所面临问题

2.1 转子槽频率与齿谐波频率混叠

从上述的描述我们可以看出，在电机运行过程中，定子电流会同时存在定子谐波电流和转子谐波电流，称之为定子槽谐波和转子槽谐波，在某种特殊情况下即定子槽数和转子槽数相等或者接近于相等时，定子槽频率和转子槽频率在频谱上发生混叠，难以辨识。以一台定子槽数为36，转子槽数为33的感应电机为例，采集其定子电流波形，然后进行快速傅里叶分解后发现，定子槽谐波和转子槽谐波次数均为11次，如图1所示，在这种情况下就很难直接在频谱图上辨识出转子槽谐波次数。

图1 定子电流频谱

为了解决上述发生混叠问题，通过对大量现场运行电机的实测分析，提出以下解决方案。即可以根据电机铭牌数据，从估算负载转差率入手，得出转子槽频率的大致区间，然后对输入端定子电流进行傅里叶分解，在之前得出的槽频率区间内找出转子槽频率。

负载率及负载转差率可根据电机输入功率P1、空载及额定参数推出:

(6)

(7)

式中：PN为额定功率；nN为额定转速；ΔP0为空载损耗；ΔPN为额定负载时损耗；n0为同步速；λ和sλ分别为基于铭牌数据得到的负载率和转差率估算值。

2.2 转子槽数的求解

在已知转子槽频率的前提下，想要辨识出电机转速的前提是转子槽数为已知量，但事实上，在大部分感应电机应用现场，电机转子槽数z2是未知量，同时，对于一些非标准系列的电机，如果想准确获得转子槽数，需要对电机进行拆卸，这是很难操作的，故这是面临的另一个难点问题。

为了能够采用一种非侵入式方法辨识出z2的具体数值，本文提出利用两个特殊工况下转速的特点，具体方法如下：

1)令电机运行在空载状态下，此时电机转速可看作同步转速，表示如下：

n1=60(fsh1±f1)/z2

(8)

2)让电机在额定负载下运行(将电流调节为额定电流)，此时电机转速即为额定转速，可表示如下：

n2=60(fsh2±f1)/z2

(9)

对式(8)和式(9)进行如下处理：

n1/n2=(fsh1±f1)/(fsh2±f1)

(10)

经过以上处理之后，只剩下fsh1,fsh2两个未知量了。在空载状态下，将分解得到的定子电流频谱中谐波较大的次数分离出来，将其视为可能的fsh1代入到式(10)中，便可以通过fsh1的公式得到fsh2的所有可能的次数；然后在额定负载状态下，将定子电流频谱中谐波较大的次数找出来，将其与之前求得的fsh2进行拟合，根据拟合的误差，即可找到正确的转子槽频率fsh2。这样，在没有得知转子槽数z2的情况下就得到了转子槽频率。此时转速是已知的，可以通过式(9)求出电机的转子槽数z2。

此外，感应电机在正常空载运行情况下，由于转差率的存在，其转子转速总是低于同步速，而此时如果仅仅用两个固定的转子槽频率fsh1,fsh2之间的配合很可能会由于误差问题导致无法找到任何一组精确的转子槽谐波具体值。因此，有必要形成一套在现场可行的未知槽数情况下转子槽频率确定方案，并考虑在实际测量和数据拟合中可能存在误差，故本文利用蒙特卡罗法，首先根据现场实际工作状况将变量误差限设置为λ=2‰，然后在此基础上在97.5%的可信度的置信区间中找出准确的转子槽频率组合。具体步骤如下：

1)在电机运行过程中，采集得到定子绕组三相电流并进行傅里叶分析，得到定子电流频谱图；

2)频谱图中峰值较低的谐波对于计算并没有实际意义，故将其从频谱图中滤掉，仅保留含量较高的谐波；

3)根据现场实际工作状况，设置空载和额定负载工况下转子转速的误差限为λ=2‰，生成正态分布数组；

4)进行蒙特卡罗循环迭代运算，给出转子槽频率的置信区间，并由此最可信地找转子槽频率组合，将迭代运算得到的转子槽频率代入式(9)便可得到转子槽数。

3 实验验证

3.1 转子槽数的计算与验证

为了验证前述所提出的四个计算步骤，利用实验室的转子槽数为28的感应电机作为算例进行分析，结果如图2所示，图2(a)，图2(b)，图2(c)，图2(d)分别对应于四个步骤。从图2中可以看出，蒙特卡罗迭代运算得到的电机空载运行情况下的转子槽频率为fsh1=1 350 Hz，此时电机转子转速视为同步速，这样就可以根据公式推得转子槽数z2为28，符合电机设计要求，且有97.5%的准确度。

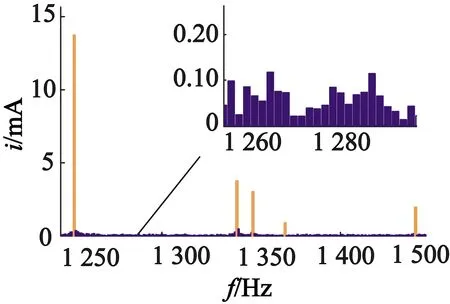
(a)定子电流频谱图

3.2 电机转速与能效的验证

为进一步验证所提出方法的可行性及实用性，针对某厂家生产的一台5.5 kW、4极笼型样机进行不同负载实验。首先利用实验所测的电气量进行转子槽数辨识，进一步利用所辨识的转子槽数辨识不同负载下的转子转速并完成能效评估，需要说明的是，能效评估时采用文献[11]中的方法。

利用本文方法辨识得到转子槽数为33，基于此，将利用转子槽频率辨识得到的不同负载点下的转速，与转速传感器测得转速进行对比，结果如表1所示。进一步得到的能效估算与实测则如图3所示。由对比结果，可以看出：

图3 电机转速及能效率评估值与实测值对比图

表1 转速实测和估算对比结果

1)实验测得的电机转速在25%负载以上时，误差值均在2%以内。例如接近满载时的转速辨识结果与实测结果几乎一致，这说明当精确辨识得到转子槽数后，转速与槽频率一一对应，辨识精度较高。

2)在25%负载或者更轻载时，误差值略大，但仍在5%以内，这主要是由于轻载时转子电流偏小，产生的谐波磁场较弱，导致定子侧电气量不太明显，而该情况下的精度，也基本满足工程的要求。

4 结 语

本文针对利用转子槽频率方法辨识笼型感应电机转速时遇到的转子槽数无法准确获得的问题，本文研究一种基于蒙特卡罗法的转子槽数及转速的辨识方法，该方法通过采集定子绕组电流波形，对其进行快速傅里叶变换得到转子槽频率，并结合蒙特卡罗循环迭代确定转子槽频率置信区间，准确获得转子槽数并完成转速辨识，提升了在现场采用转子槽频率辨识电机转速方法的可行性。对一台5.5 kW笼型感应电机进行了实验验证，并基于本文方法实现了基于可测电气量的电机系统能效在线辨识，为工业生产中电机系统的能效评估提供了重要技术参考和理论支持。