三种群捕食系统动力行为与最优捕获策略

冯庆红, 陈荣军, 冯艳青, 王忠英, 陈立范

(1. 常州工学院理学院, 江苏 常州 213032; 2. 上海健康医学院文理教学部, 上海 201318)

B-D功能反应函数考虑了捕食者之间的相互竞争, 比Holling反应函数[1]更加贴近实际．对带B-D功能反应函数的食饵捕食模型, 众多学者分析了各种因素对系统的影响, 如扩散[2-3]、食饵避难所[4-5]、脉冲反馈控制[6]、分支[7-8]、Allee效应[9]、时滞[10-11]、 阶段结构[12-13]以及捕获[14]等．由于捕获问题既关系到经济效益, 又与保护物种和生态环境有关, 自然引起了生物数学学者的极大关注．最近, Haugen等[14]提出一种基于优化的拖网作业规划系统, 建立了一个最优控制问题的公式, 为渔船和渔网自主捕鱼找到了可行的轨迹; He等[15]建立了一类具全局反馈边界条件和年龄结构的非线性偏微分方程模型,并利用紧致性和最大化序列确定了最优捕获策略．受上述工作启发, 本文拟讨论带B-D功能反应函数的三种群捕食系统, 并对系统中2个竞争捕食者种群同时进行捕获的最优策略进行分析．

1 三种群捕食系统

三种群捕食系统为

(1)

其中u,v,ω分别表示t时刻食饵种群和两竞争捕食者种群的密度;r表示食饵种群的内禀增长率;k表示食饵种群的最大环境容纳量;αv/(a+bu+cv)表示B-D功能反应函数;d表示捕食者种群v的死亡率;γ表示捕食者种群ω的内禀增长率;μ表示捕食者种群ω和食饵种群u在平衡状态下生物量之比;q2,q3分别表示对捕食者种群v和ω的可捕系数;E2,E3分别表示相应的捕获努力量．假设所有参数为正数, 显然γ-q3E3>0．据生态学意义, 仅在区域{(u,v,ω)|u>0,v>0,ω>0}=R+内对系统(1)进行讨论．

2 正平衡点的存在性与唯一性

定理1系统(1)存在唯一正的平衡点．

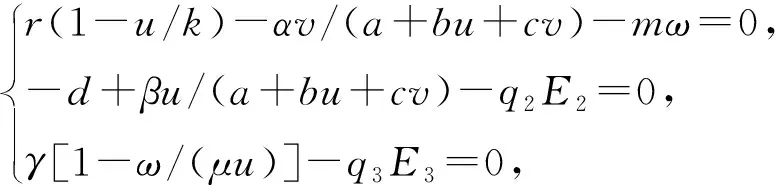
3 正平衡点的局部渐近稳定性

定理2当cβ>bα,r/k>bα,γb>μβ,c>1时,正平衡点局部渐近稳定．

证明 令f1(u,v,ω)=ru(1-u/k)-αuv/(a+bu+cv)-muω,f2(u,v,ω)=v[-d+βu/(a+bu+cv)]-q2E2v,f3(u,v,ω)=γω[1-ω/(μu)]-q3E3ω, 则系统(1)在正平衡点(u*,v*,ω*)处的Jacobian矩阵为

设对应的特征值方程λ3+Dλ2+Fλ+G=0, 可知:G>0; 当cβ>bα时,D>0; 且当cβ>bα,r/k>bα,γb>μβ,c>1时,DF-G<0. 根据Routh-Hurwitz判别法, 在上述条件下, 矩阵A的所有特征值都有负实部, 因此正平衡点局部渐近稳定．

4 经济平衡点

假设两竞争捕食者种群v,ω的捕捞成本分别为常数c2,c3, 出售单价分别为常数p2,p3, 通过捕获获得的经济效益分别为L2=(p2q2v-c2)E2和L3=(p3q3ω-c3)E3, 则总捕获效益L=(p2q2v-c2)E2+(p3q3ω-c3)E3．显然, 当L2>0,L3>0时, 捕获效益大于捕获费用, 可以对两竞争捕食者种群进行捕获．

经济平衡点不同于生物平衡点, 它是在经济利润被完全消耗时获得的平衡点(u∞,v∞,ω∞,E2∞,E3∞), 满足

解此方程组可得v∞=c2/(p2q2),ω∞=c3/(p3q3)．当{ar/k+rcc2/(kp2q2)-b[mc3/(p3q3)-r]}2>4brαc2/(kp2q2)时,u∞存在, 且E2∞=βu∞/[q2(a+bu∞+cv∞)]-d/q2,E3∞=γ[1-ω∞/(μu∞)]/q3．由此可得如下定理．

定理3当{ar/k+rcc2/(kp2q2)-b[mc3/(p3q3)-r]}2>4brαc2/(kp2q2)时, 系统的经济平衡点(u∞,v∞,ω∞,E2∞,E3∞) 存在．

5 最优捕获策略

最优捕获问题可以转化为如下的最优控制问题, 其目标函数为max{J},使得

(2)

其中Ei(i=2,3)为捕获控制变量, 且0≤Ei≤Emax．

定理4系统 (1) 满足条件{ar/k+rcc2/(kp2q2)-b[mc3/(p3q3)-r]}2>4brαc2/(kp2q2)时, 存在唯一最优平衡解(uδ,vδ,ωδ); 相应地,对两竞争捕食者种群v,ω的最优捕获努力量分别为E2δ=βuδ/[q2(a+buδ+cvδ)]-d/q2和E3δ=γ[1-ωδ/(μuδ)]/q3．

证明 首先, 构建此问题的Hamilton函数H=e-δt[(p2q2v-c2)E2+(p3q3ω-c3)E3]+λ2{v[-d+βu/(a+bu+cv)]-q2E2v}+λ3{γω[1-ω/(μu)]-q3E3ω}, 其中λ1(t),λ2(t),λ3(t)为伴随变量, 伴随方程为

dλ1/dt=-∂H/∂u=-λ1[r(1-2u/k)-αv(a+cv)/(a+bu+cv)2-mω]-
λ2βv(a+cv)/(a+bu+cv)-λ3γω2/(μu2),
dλ2/dt=-∂H/∂v=-e-δtp2q2E2+λ1αu(a+bu)/(a+bu+cv)2-
λ2[-d+βu(a+bu)/(a+bu+cv)2-q2E2],
dλ3/dt=-∂H/∂ω=-e-δtp3q3E3+λ1mμ-λ3γ+2λ3γω/(μu)-q3E3．

考虑最优平衡解, 由系统(2)得E2=βu/[q2(a+bu+cv)]-d/q2,E3=γ[1-ω/(μu)]/q3．

假设系统在Ei=0或Ei=Emax时不会出现平衡点, 则根据Pantryagin最大值原理, 最优捕获控制量Ei(i=2,3)在极值点达到, 此时∂H/∂E=0, 则有λ2=-e-δt[p2-c2/(q2v)],λ3=-e-δt[p3-c3/(q3ω)]．伴随方程可写成dλ1/dt-A1λ1=-B1e-δt, 得λ1=B1e-δt/(A1+δ), 其中

A1=ru*/k-bαu*v*/(a+bu*+cv*)2,

B1=βv*(a+cv*)[p2-c2/(q2v*)]/(a+bu*+cv*)+
γω*2[p3-c3/(q3ω*)][bαu*v*/(a+bu*+cv*)2-ru*/k]/(μu*2)．

同理,可得λ2=B2e-δt/(A2+δ),λ3=B3e-δt/(A3+δ), 其中A2=cβu*v*/(a+bu*+cv*)2,B2=p2[βu*/(a+bu*+cv*)-d]-B1αu*(a+bu*)/[(A1+δ)(a+bu*+cv*)2];A3=γω*/μu*,B3=p3γ[1-ω*/(μu*)]-B1mu*/(A1+δ)．于是得到奇异轨线为p2-c2/(q2v*)=B2/(A2+δ),p3-c3/(q3ω*)=B3/(A3+δ)．

令f(v*)=p2-c2/(q2v*)-B2/(A2+δ), 显然limv*→0+f(v*)<0．若存在k>0使f(k)>0, 并且对任意v*>0, 显然有f′(v*)>0．则根据零点定理, 在区间(0,k)内, 方程f(v*)=0存在唯一的正根v*=vδ．同理可得ω*=ωδ．再由式(2)中r(1-u*/k)-αv*/(a+bu*+cv*)-mω*=0, 可得唯一u*=uδ, 故E2δ=βuδ/[q2(a+buδ+cvδ)]-d/q2,E3δ=γ[1-ωδ/(μuδ)]/q3．