基于MDP和动态规划的医疗检查预约调度优化方法研究
2020-10-24梁峰,徐苹
梁 峰, 徐 苹
( 南开大学 商学院,天津 300071)
0 引言
医疗检查是医院服务过程的中间环节,既面向各大科室,又面向多类患者,其图像结果是医生诊断病情的重要依据。由于购置成本高昂,操作维护复杂,医院的大型诊疗设备数量有限,每天的最大服务能力受到约束。随着就医病人持续增加,各大检查科室压力增大,在可允许的等待时间内,医院的检查资源难以满足所有病人的需求。如何通过合理有效的方式,将可用的医疗设备资源在不同类型的病人间进行分配,以提高医院的收益并减少病人的等待,是医院管理面临的重要问题。
检查资源的需求来自多种病人,这些病人一般可分为三类:门诊病人、住院病人、急诊病人。不同类型的病人具有各自的需求特征。门诊病人和住院病人大多会选择提前预约,而急诊病人会在服务日当天随机到达。急诊病人病情紧急,可允许的等待时间短,一般在急诊病人到达时,医院需立即安排检查,否则会造成较高的拒绝成本。门诊病人和住院病人病情相对缓和,可允许适当等待。另外,在实际中,不同类型的病人所需要的检查时间也会有所不同。
医疗检查资源的有效管理主要包含两大任务:一是建立起面向病人的检查预约系统,病人可以通过提前预约以减少服务日当天的无效等待。二是确定预约系统的决策规则,在病人的预约请求到达时,系统要能够根据规则做出接受或者拒绝的决定。目前,大部分医院设有预约中心来处理各类病人的预约请求,预约系统一般会根据先到先得(First Come First Served,FCFS)的决策方式,将病人的请求安排到设备最近的空闲时间段。这种预约排程方式不考虑不同类型病人的需求特征,同时,由于检查资源的稀缺性,医院将有可能拒绝后到达但收益更高的病人类型。为解决此类问题,本文根据有限时域马尔可夫决策(Markov decision process,MDP)模型,研究有限检查资源在不同类型病人间的最优预约调度:以医院在检查设备方面收益最大化为目标,建立有限时域马尔可夫决策(MDP)模型,并结合动态规划理论,得出系统最优的预约排程策略。
1 文献综述
关于医疗检查资源的预约调度,国外已有广泛的研究。文献[1]考虑多优先级病人不同的到达率和爽约率,利用马尔可夫决策(MDP)模型进行预约调度优化,决定有限的检查资源在不同类型的病人间如何分配,突出之处在于提出了利用两种算法和一种数学规划来解决复杂维度的MDP模型。文献[2]也是针对不同病人类型间的检查资源分配问题,建立了连续时间马尔可夫决策模型,考虑设备服务时间的随机性和部分病人的不守时因素,优化目标为医院获得最大收益,并通过近似动态规划的方法进行求解。文献[3]运用MDP模型,研究在服务日当天,医院如何将多台检查设备在三类病人间进行合理分配以获得最大收益。文献[4]研究放射科的预约排程问题,建立了连续时间马尔可夫决策模型,考虑折扣因子,通过合理转化,用线性规划代替近似动态规划来求解MDP模型。文献[5,6]也是运用线性规划的方式求解MDP模型。文献[7~9]研究病情紧急的中风病人的检查排程问题,提出签约时间段CTS(Contracted Time Slots)的方式,即检查系统会为中风病人预留CTS,三篇论文均是结合MDP模型与动态规划理论,分别研究CTS分配,中风病人的合理排程和部分病人提前取消CTS的解决方案。
文献[10]针对化疗科室病人的预约排程问题,建立包含多目标的整数规划模型,利用Cplex程序来进行求解,分析不同时间长度下的预约调度策略。文献[11]在考虑病人爽约和病人偏好(即病人自身希望哪天进行检查)的基础上,建立起根据预约状态变化的动态模型,并利用启发式算法来求解出最优策略,通过比较证明该预约策略的优越性。文献[12]将随机因素考虑在内,运用近似动态规划模型研究多种资源的分配问题和多类病人的排程问题,通过算例比较,证明近似动态规划方法在处理病人排程问题方面的优越性。
近几年,国内一些学者也都开始研究医疗检查资源的调度优化问题。文献[13]利用MDP模型和动态规划理论,研究一台设备、三类病人条件下检查设备的预约调度。文献[14]研究的情况为三类病人、两项检查、且各类病人可允许的等待时间都为一天,建立包含有限时域的MDP模型,通过值迭代算法得出各类病人的最优预约排程策略。文献[15]考虑病人的不守时因素,根据CT检查室现有排程规则,利用Simio软件建立仿真模型,证明该模型的合理性与有效性,并在此基础上寻求优化的排程方案。文献[16]也是利用仿真方法,实地调查所研究医院的放射科现状,建立起针对核磁共振检查(MRI)的分时段预约模型,设计出三种新的排程规则,并通过遗传算法进行优化,后与传统预约策略比较,证明新规则的优越性。
目前,对于病人的预约排程问题,各学者考虑的内容有所不同,采取的求解方法也都各异,为进一步的研究确立了基础。在关于医疗检查资源优化调度的现有文献中,由于模型的建立和求解会随着考虑因素的增加而变得复杂,大部分研究对不同病人的需求特征考虑的不够完整,研究多台检查设备的文献仍为少数,更很少有学者考虑不同类型病人所需的检查时间不同,而病人检查时间的不同将会影响系统产能的最优调度。本文考虑的情况为两台设备、三类病人且各类病人所需要的检查时间不同,根据合理假设,建立有限时域马尔可夫决策模型,利用matlab软件求解得出最优预约调度策略,并通过敏感性分析研究了预约策略的适用性。
2 模型描述
本文针对两台设备、三类病人的情况进行最优预约排程策略的研究。每类病人需要的检查时间有所不同,收益情况也存在差别。预约排程的目标是医院在检查设备方面获得最大收益。当某类病人的预约请求到达时,系统会根据决策规则立刻做出接受或者拒绝该请求的决定,并根据设定的排程规则做出合理的预约排程。
2.1 模型假设
假设1医院安排设备A和设备B同时为病人服务,这两台设备的新旧程度、服务能力等完全相同。
假设2检查设备的服务能力通过时间槽(Time Slot)来衡量,根据实际情况,时间槽可设定为时间的基数,设备A与设备B每天可用的最大时间槽个数相同。
假设3不同类型的病人所需要的检查时间不同,并且各类病人的检查时间可以通过时间槽的个数来表示,住院病人所需检查时间比门诊病人所需检查时间长。
假设4整个预约周期可划分为有限个相等的时刻。在任意的预约时刻,门诊病人与住院病人的预约请求根据不同的概率到达系统,且到达情况相互独立。急诊病人会在检查当天随机到达。
假设5在任一预约时刻,每台设备最多只有一位病人的预约请求到达,即系统在任一预约时刻最多有两位病人的预约请求到达。
假设6设备A和设备B的到达情况相互独立。在任一预约时刻,每台设备都有三种可能,即到达一位门诊病人的预约请求、到达一位住院病人的请求和没有预约请求到达。
假设7在任一预约时刻,预约系统的排程规则设置如下:如果系统只接受一位病人(门诊病人或住院病人)的预约请求,优先选择剩余产能多的设备为该病人服务,若两台设备剩余产能相同,则选择设备A为病人服务;如果系统接受一位门诊病人、一位住院病人的预约请求,优先选择剩余产能多的设备为住院病人服务,若两台设备剩余产能相同,则选择设备A为住院病人服务;如果系统接受两位同类型病人(两位门诊病人或两位住院病人)的预约请求,则两台设备各服务一位病人。
基于以上假设,医疗检查预约调度问题可以通过有限时域马尔可夫决策过程(MDP)来进行描述,医院收益最大化的目标也可以转化为动态规划的最优解。MDP模型可以在任一预约时刻,根据系统的状态和病人的到达情况做出满足条件的最优决策。
2.2 模型参数设置
现假设设备A和设备B每天的最大可用时间槽数分别为个,则检查系统每天总可用时间槽数为个。将整个预约周期划分为个相等的预约时刻,即预约周期的所有预约时刻可表示为t=H,H-1,…,2,1,病人的预约请求在这些时刻按一定概率到达,假设t=H为预约周期的开始,t=0为预约周期的结束,即服务日当天的开始。模型中的其他参数设置如表1所示。
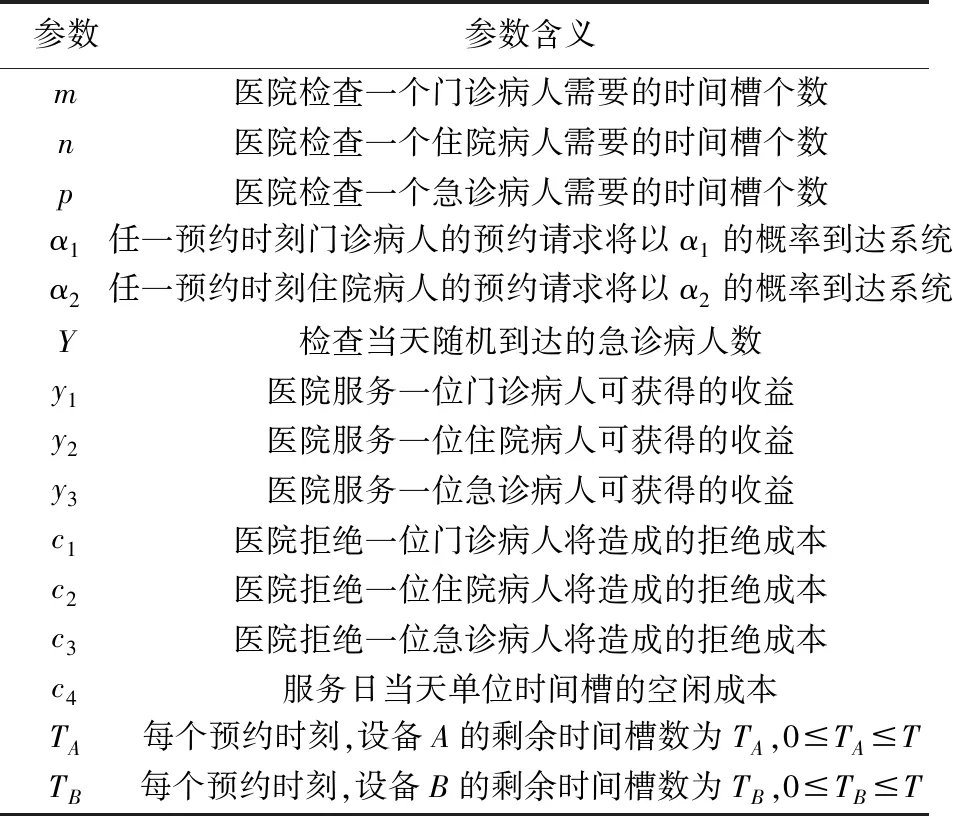
表1 模型参数设置
2.3 模型建立
根据马尔可夫决策的六大要素:决策阶段、状态集合、决策集合、转移概率、报酬、目标函数,建立预约周期内的MDP模型如下。
2.3.1 决策阶段
预约周期内的任一预约时刻t,即t=H,H-1,…,2,1。
2.3.2 状态集合
TA表示设备A的剩余可用时间槽数,TB表示设备B的剩余可用时间槽数。S=(TA,TB)为系统的状态集合,满足0≤TA≤T, 0≤TB≤T。
2.3.3 决策集合
每一预约时刻t=H,H-1,…,2,1,系统根据当前剩余时间槽数和病人的到达情况做出决策,即接受或者拒绝的病人的预约请求。系统的行动集合用At(TA,TB)来表示,其中0代表拒绝病人的预约请求,1代表接受病人的预约请求。即有
2.3.4 转移概率
每台设备在任一预约时刻都有三种预约到达可能,即到达一位门诊病人的预约请求、到达一位住院病人的预约请求和没有预约请求到达,则预约系统在任一时刻的到达情况可能有六种,对应六种不同的转移概率。表2列出了六种可能的到达情况及其相应的转移概率。

表2 到达情况与转移概率
2.3.5 报酬
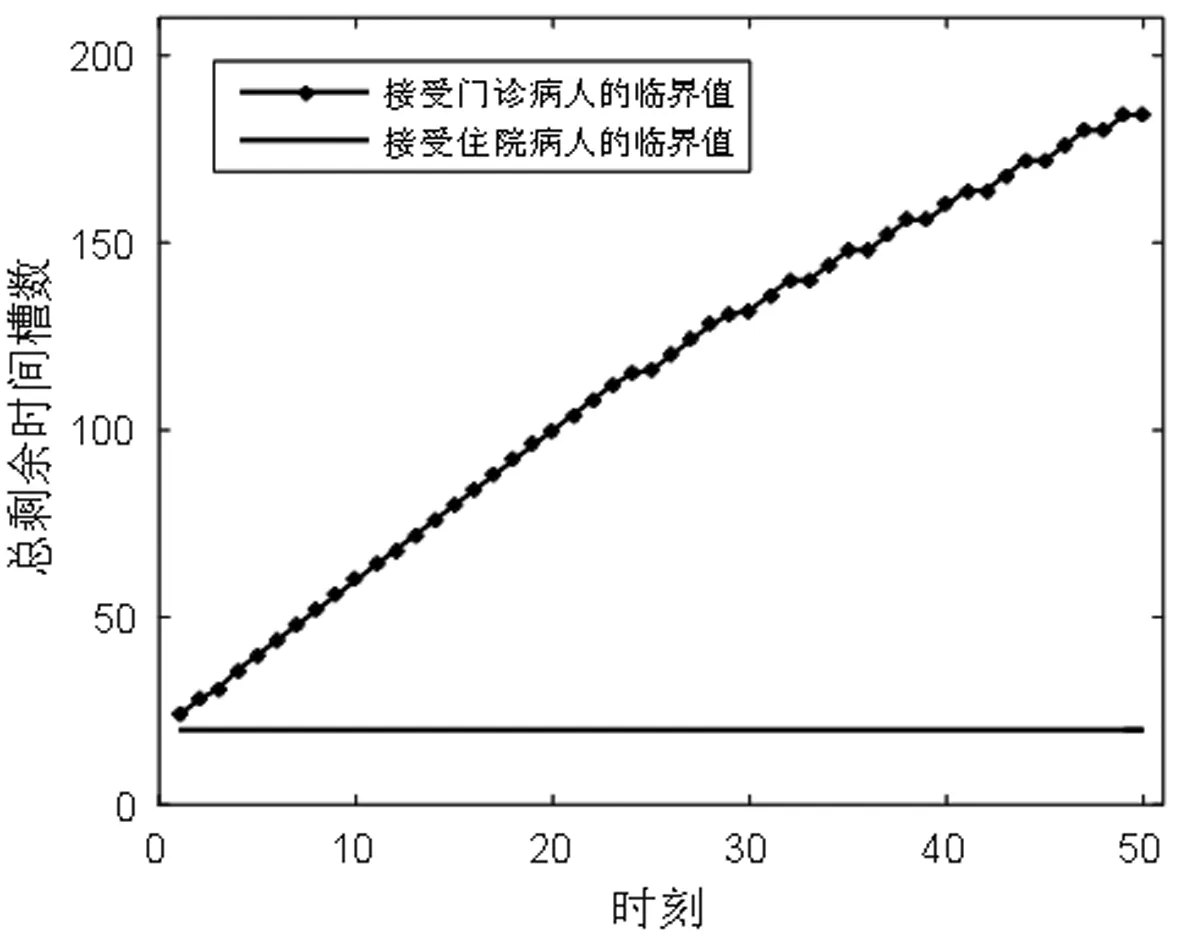
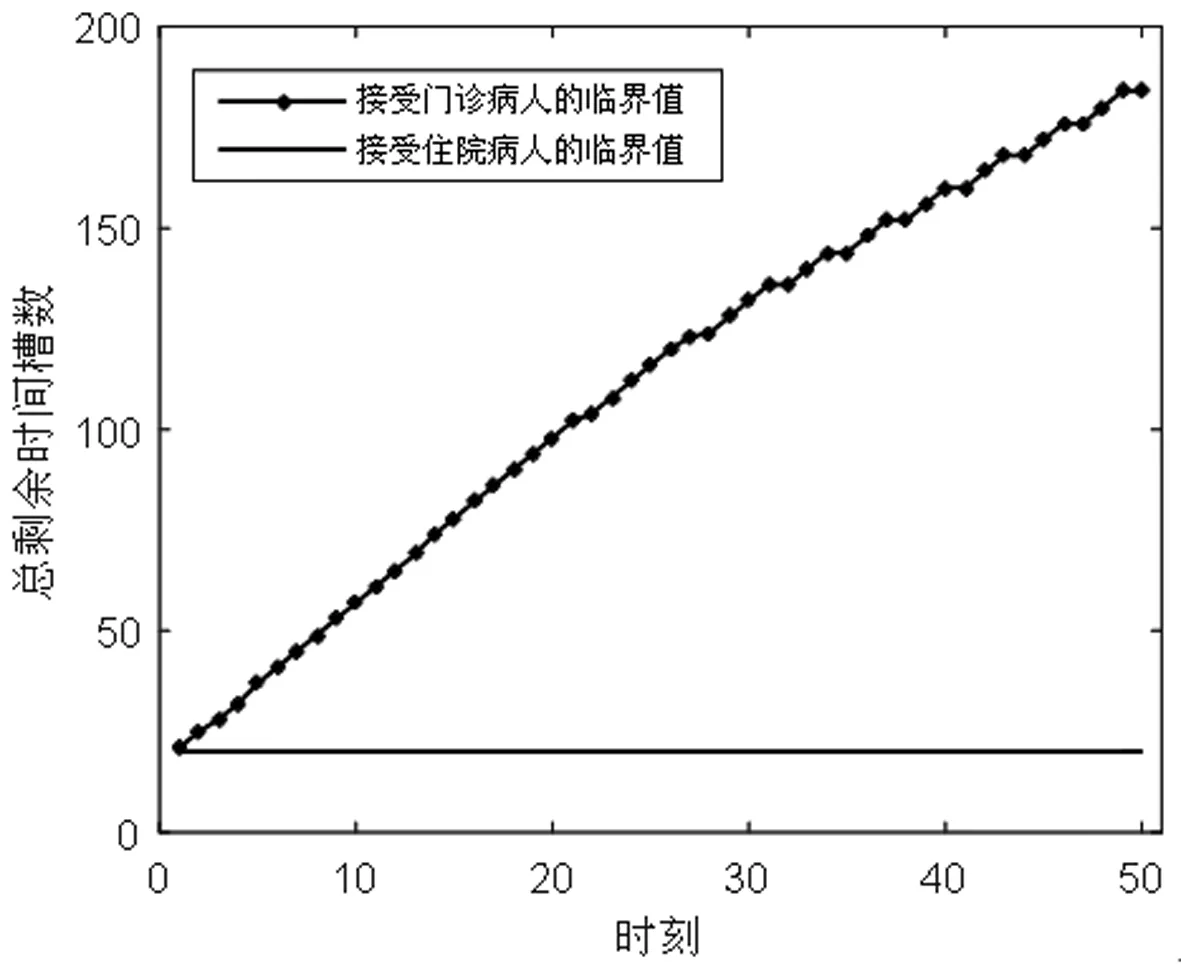
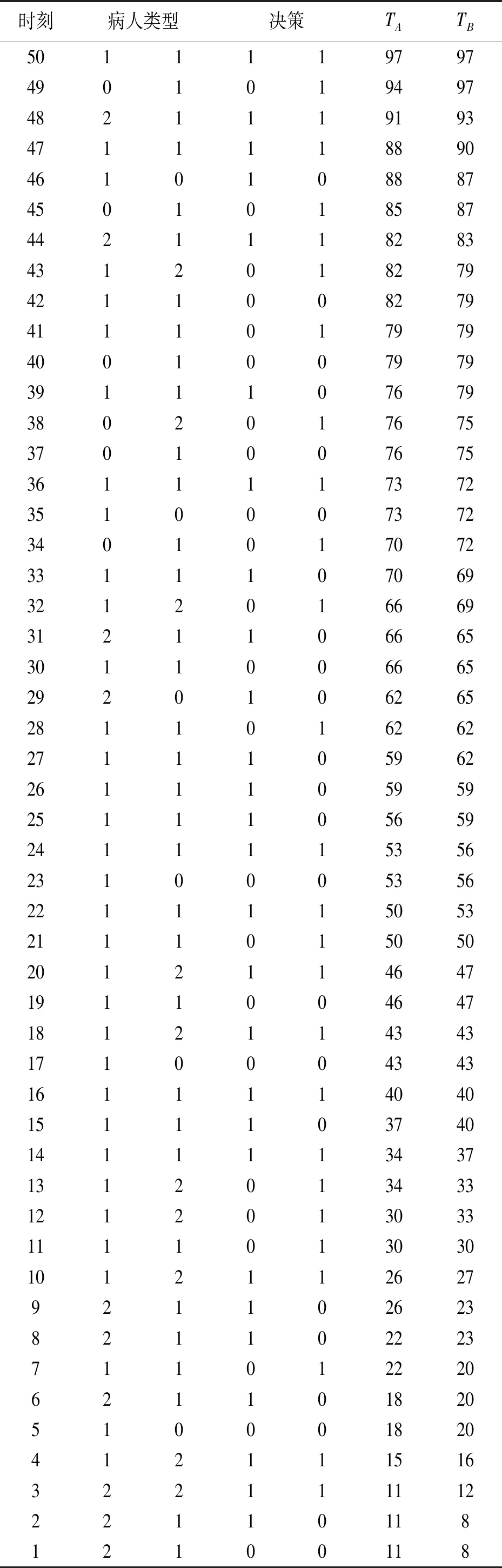
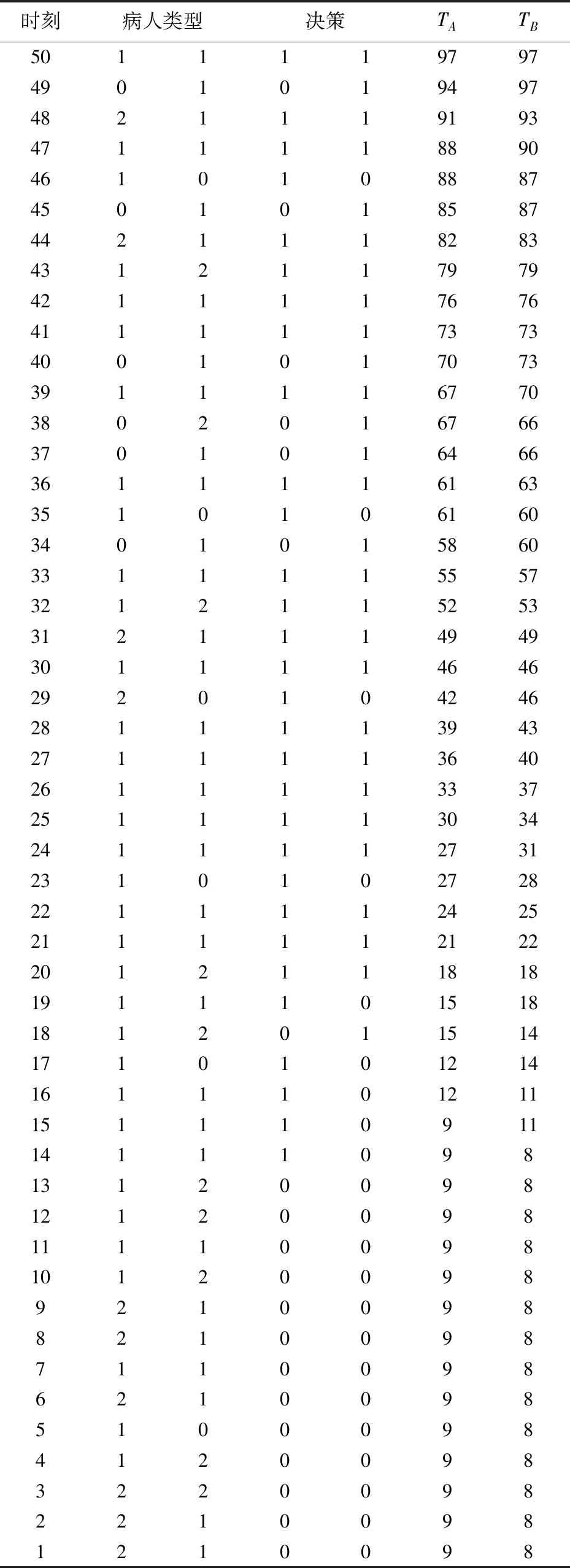
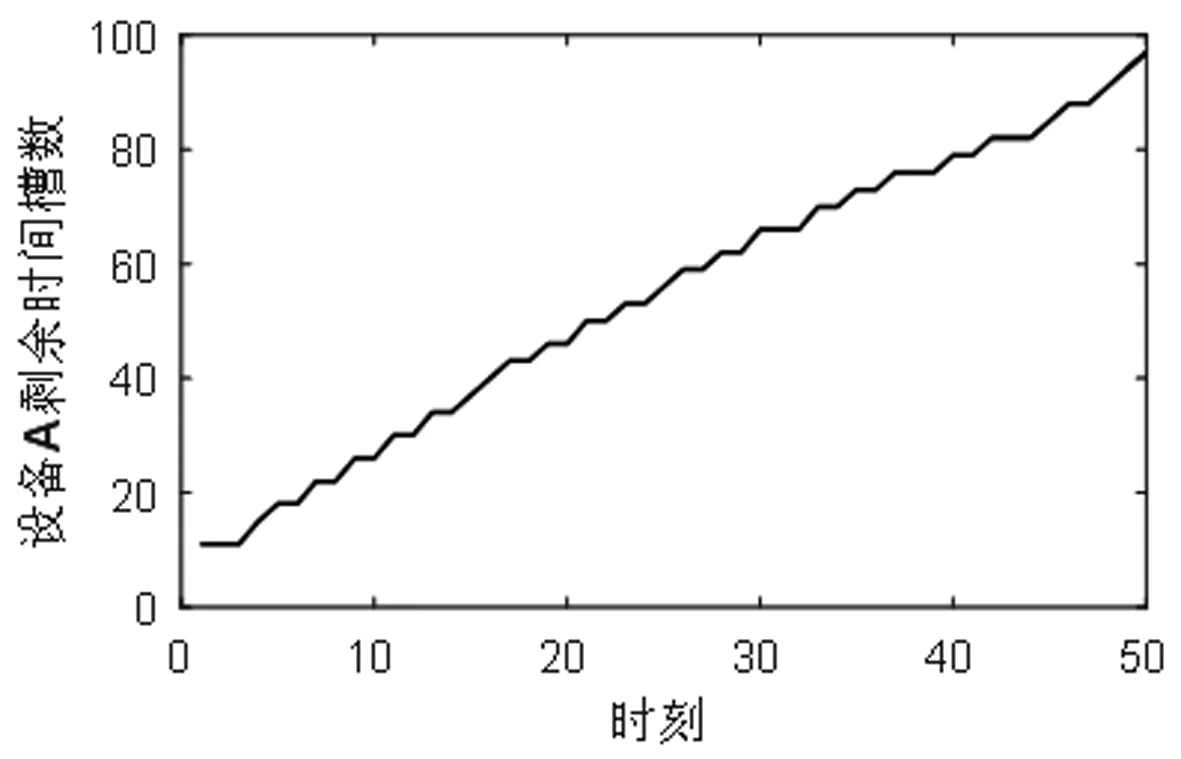
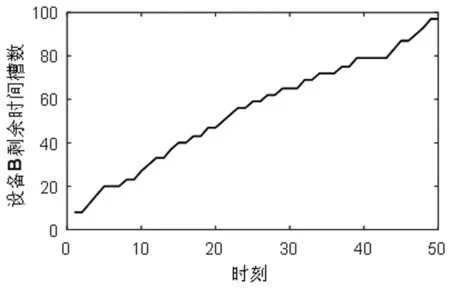
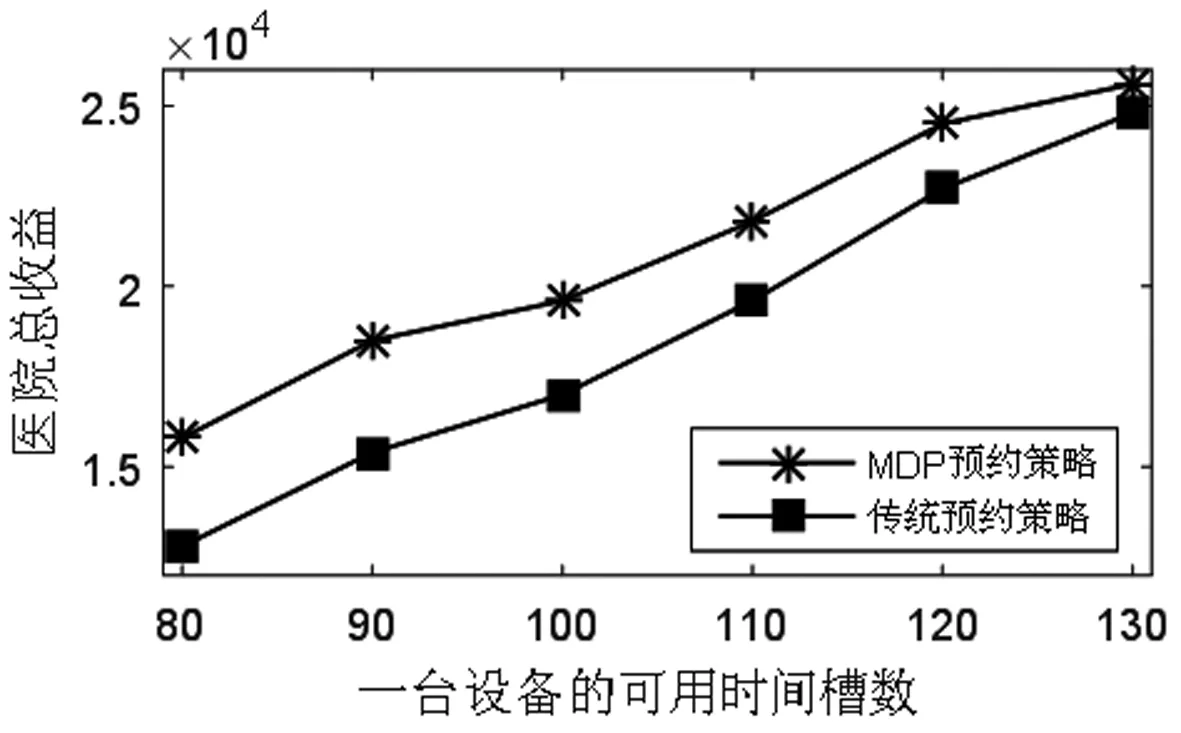
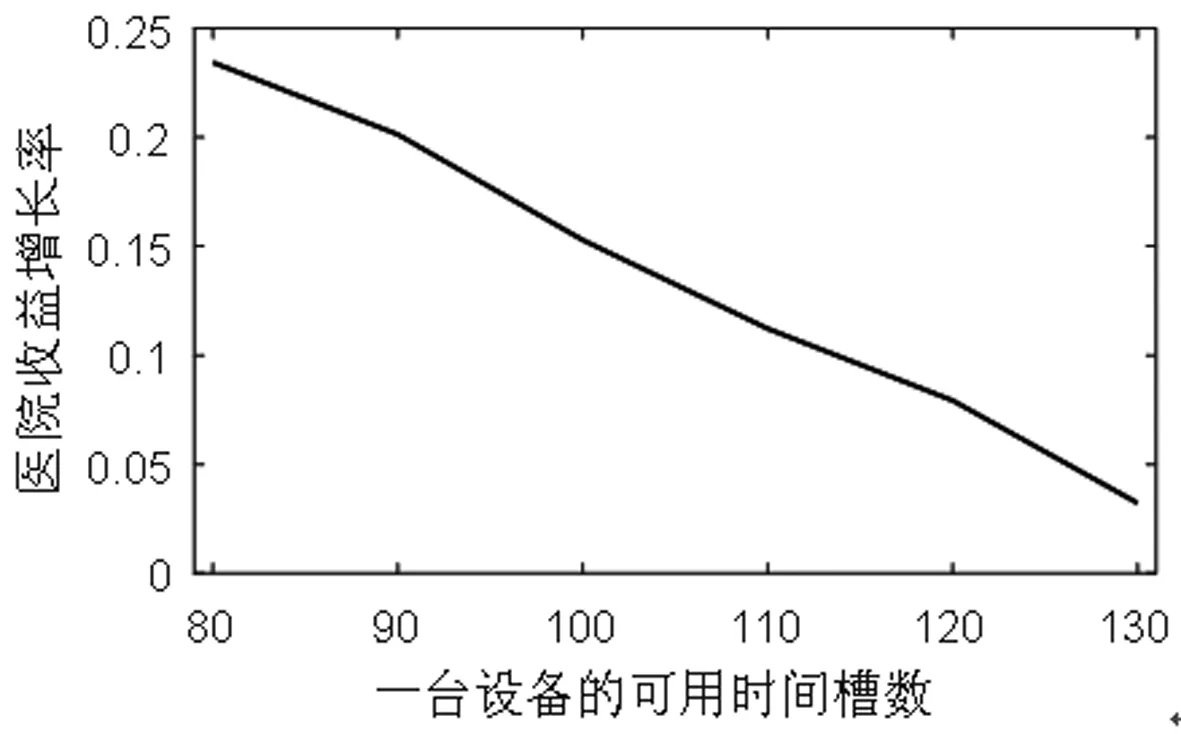
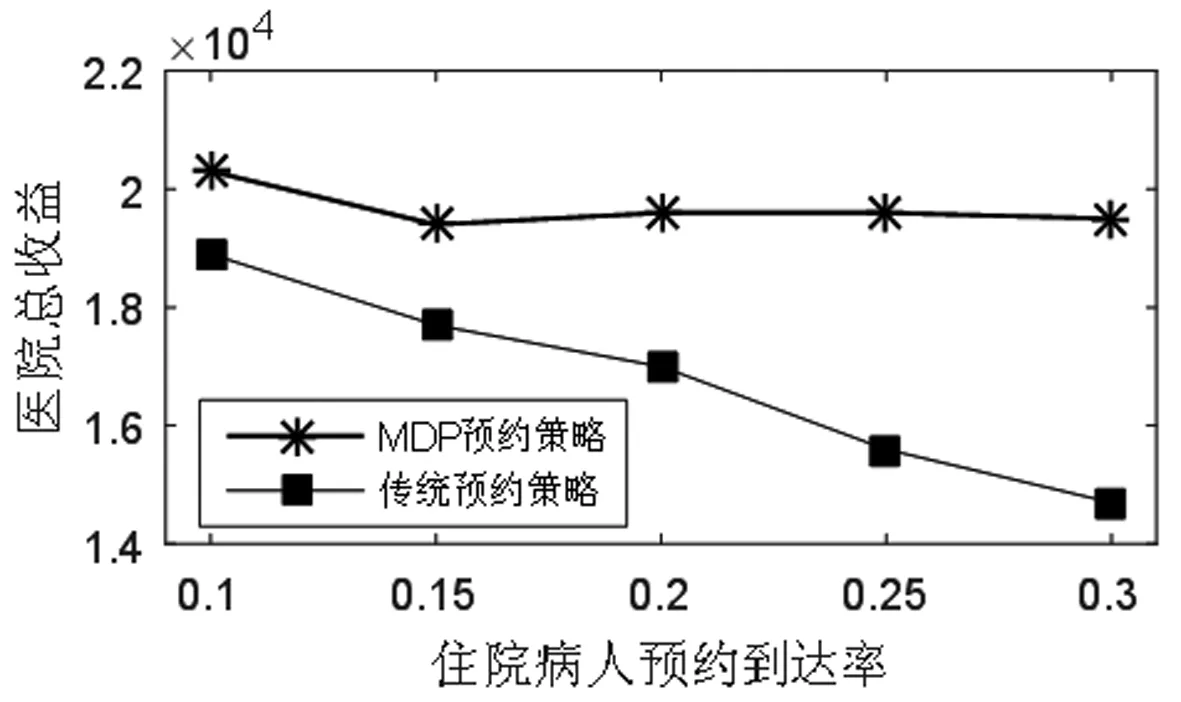
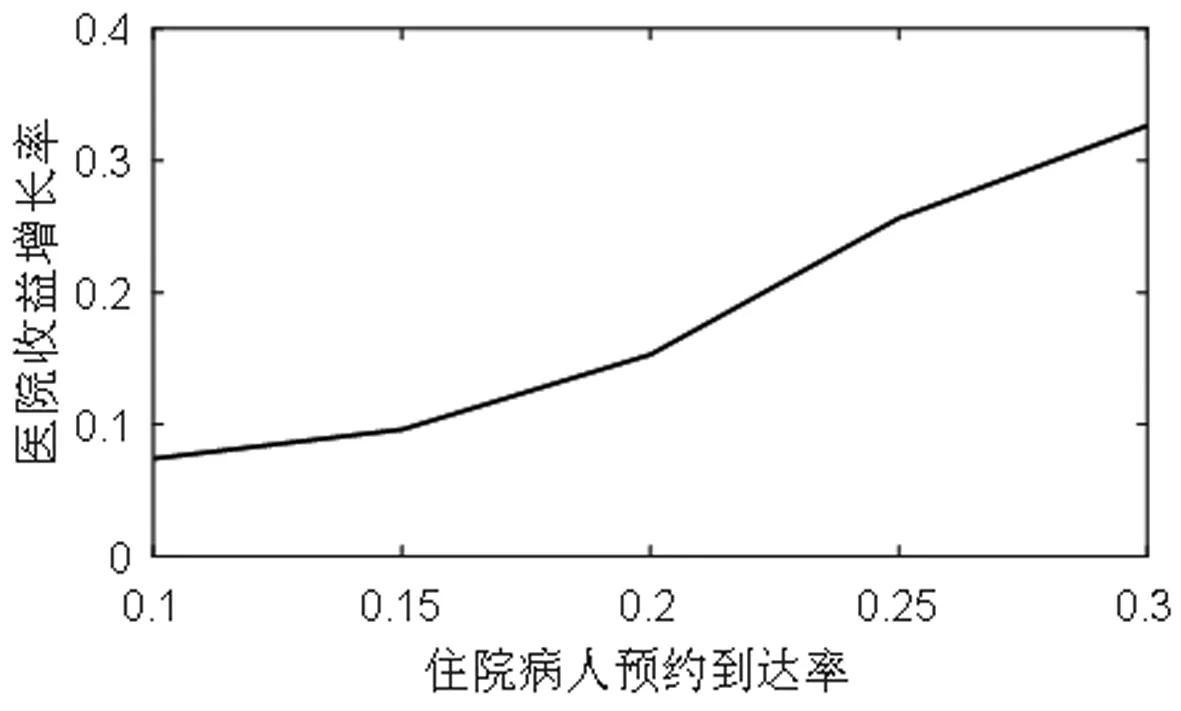
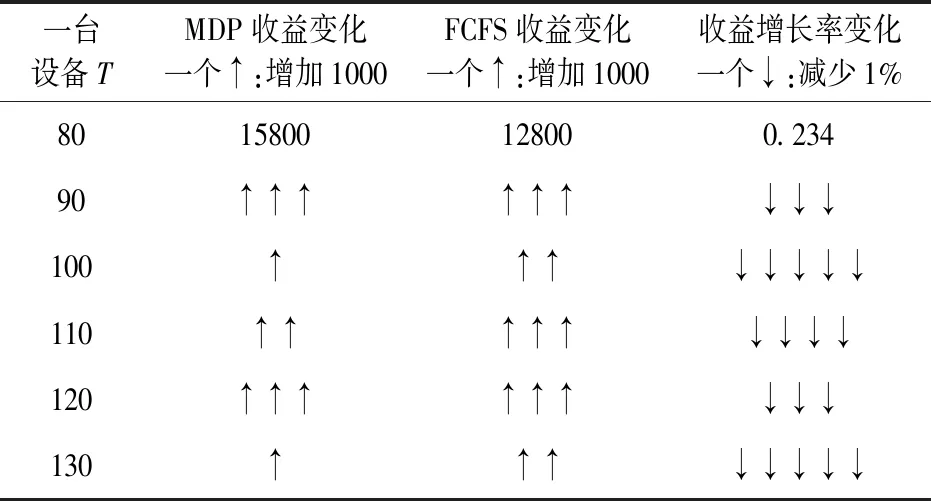
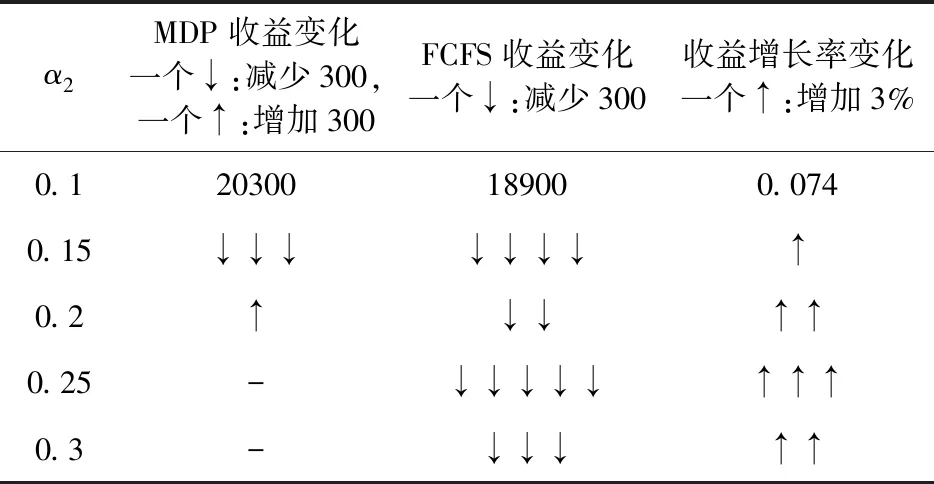
医院检查一位门诊病人、住院病人、急诊病人的收益分别是y1,y2,y3,相应的,拒绝一位门诊病人、住院病人、急诊病人的成本分别是c1,c2,c3。一般有y1+c1 2.3.6 目标函数 Jt(TA,TB)表示从t时刻,系统的当前状态S=(TA,TB)开始,一直到预约周期结束医院所能获得的最大收益。 (1) 其中,当两个门诊病人的预约请求到达,即i=1时, (2) 当两个住院病人的预约请求到达,即i=2时, (3) 当一个门诊病人和一个住院病人的预约请求到达,即i=3时, (4) 当只有一个住院病人的预约请求到达,即i=4时, (5) 当只有一个住院病人的预约请求到达,即i=5时, (6) 当没有预约请求到达,即i=6时, (7) 当检查预约周期结束,服务日当天开始,即t=0时,急诊病人开始到达,随机到达的急诊病人数为Y。一个急诊病人所需检查时间为p个时间槽,系统的状态S=(TA,TB),当[TA/p]+[TB/p]>Y([a]表示不大于a的最大整数),即总剩余时间槽所能服务的急诊病人数大于当天实际到达的急诊病人数时,系统会产生空闲成本,同样的,当[TA/p]+[TB/p] J0(TA,TB)=y3E(TS^Y)-c4[TA+TB-E(TS^Y)×p]-c3E(Y-TS)+ =(y3+c3+c4×p)E(TS^Y)-c3E(Y)-c4(TA+TB) (8) 在公式(8)中,(a^b)表示min(a,b),(a)+表示max(a,0)。 根据MDP模型,At(TA,TB)为使得系统收益函数(公式(1))最大化的行动集合。在所有预约时刻t=H,H-1,…,1,根据边际条件(公式(8))的限制,确保最优解的存在。在合理设置参数后,可以利用值迭代策略求解MDP模型,使得系统在每一时刻,都能根据剩余时间槽数和病人的到达情况做出最优决策,即接受或者拒绝一个病人的预约请求,并根据设置的排程规则得出具体排程策略。 任一预约时刻,设备A和设备B各自有三种到达情况,到达一个门诊病人的预约请求、到达一个住院病人的预约请求和没有预约请求到达。将两台设备的预约到达情况相结合,系统在任一预约时刻都有六种可能的到达情况(表2)。在任一预约时刻t=H,H-1,…,1,系统状态S=(TA,TB)时,如果到达一个门诊病人的请求,系统需比较Jt-1(TA+TB-m)+y1与Jt-1(TA+TB)-c1的大小,若y1+c1≥Jt-1(TA+TB)-Jt-1(TA+TB-m),则接受该门诊病人的请求,否则拒绝。如果到达一个住院病人的请求,则需比较Jt-1(TA+TB-n)+y2与Jt-1(TA+TB)-c2的大小,若y2+c2≥Jt-1(TA+TB)-Jt-1(TA+TB-n),则接受该住院病人的请求,否则拒绝。根据这样的决策规则,通过多级迭代,任一预约请求到达时,系统都可以自动做出最优决策。在做出是否接受某位病人的决策后,系统会根据当前时刻的接受情况及设定的排程规则得出排程策略。 为了更好的模拟出各类病人的到达情况和系统的最优决策过程,对MDP模型中的各项参数进行设置。将预约周期平均划分为50个相等的时刻,即H=50,此时病人的到达时刻和系统的决策时刻为任一预约时刻t,其中t=50,49,…,1。设备A和设备B每天的最大可用时间槽数T=100,检查一位门诊病人所需时间槽数m=3,检查一位住院病人所需时间槽数n=4,检查一位急诊病人所需时间槽数p=1。三类病人各自对应的收益和拒绝成本设置如下:y1=200,y2=400,y3=600,c1=100,c2=300,c3=500。每个时间槽的空闲成本c4=100。门诊病人的预约请求在任一时刻以α1=0.7的概率随机到达,住院病人的预约到达率α2=0.2。检查当天,随机到达的急诊病人数Y服从参数为15的泊松分布。根据各类病人的请求到达概率可计算得出系统在任一预约时刻的转移概率pi(其中i=1,2,3,4,5,6),相应的到达情况和六种转移概率值如表3所示。 表3 到达情况与转移概率值 基于以上参数设定,根据动态规划理论,可利用matlab软件对马尔可夫决策(MDP)模型进行仿真求解。根据门诊病人和住院病人的预约请求到达率α1,α2,可以模拟出预约周期内的一组到达情况,通利用多级迭代,得出最优排程策略。在本文的算例中,通过观察,发现系统会产生对于接受各类病人的临界值。以门诊病人为例,在任一预约时刻,存在这样的临界值L,L为使得y1+c1≥Jt-1(TA+TB)-Jt-1(TA+TB-m)成立的最小值,故决策规则可简化为比较TA+TB与L的大小,TA+TB≥L时,可保证y1+c1≥Jt-1(TA+TB)-Jt-1(TA+TB-m)一定成立,故接受病人的请求,否则拒绝。对于住院病人,同样存在这样的临界值。系统做出接受或拒绝的决策后,根据接受情况进行排程,若只接受一位病人的预约请求,优先选择剩余产能多的设备为病人服务(TA=TB时选择设备A);若接受一位门诊病人、一位住院病人的预约请求,优先选择剩余产能多的设备为住院病人服务(TA=TB时选择设备A服务住院病人);若接受两位同类型病人,则两台设备各自服务一位病人。根据仿真结果,医院的期望收益函数Jt(TA,TB)随预约时刻和总剩余时间槽的变化情况如图1所示。由于系统在每一预约时刻有两位病人的预约请求到达,故在任一时刻,系统接受第一位病人(门诊病人或住院病人)的临界值变化如图2所示,接受第二位病人的临界值变化如图3所示。 图1 医院期望总收益变化图 图2 系统接受第一位病人的临界值变化图 图3 系统接受第二位病人的临界值变化图 根据MDP模型的决策规则及设定的排程规则,预约周期内的最优排程策略如表4所示。传统预约策略的决策过程如表5所示。在病人类型中,1代表一位门诊病人的预约请求到达,2代表一位住院病人的预约请求到达,0代表没有预约请求到达。在决策中,1用来表示接受一位病人的预约请求,0用来表示拒绝一位病人的预约请求。TA表示设备A在当前时刻的剩余可用时间槽数,TB示设备B在当前时刻的剩余可用时间槽数。 表4 MDP预约策略 表5 传统预约策略 根据MDP的决策过程,两台设备的剩余时间槽个数随预约时刻的变化情况分别如图4、图5所示。设备剩余时间槽变化情况对应检查当天的排程策略,由于系统总排程规则为在任一预约时刻,优先选择剩余产能多的设备为病人服务,故两台设备的剩余时间槽变化情况相近,实现了产能的均衡利用,符合检查当天两台设备同时服务的实际情况。 图4 设备A剩余时间槽变化图 图5 设备B剩余时间槽变化图 根据本文的预约策略,系统在预约周期内所能获得最大总收益为19600,而传统的先到先得(FCFS)的预约策略所能带来的收益为17000。通过比较,可以证明本文的预约排程策略为更优的排程方式。 其他条件不变的情况下,改变两台设备每天可用的最大时间槽数T,医院的总收益随系统总产能的变化情况如图6所示。可得出结论:(1)当两台设备的总产能不能满足所有病人的预约请求时,无论是传统预约策略还是MDP预约策略,医院总收益都随着可用时间槽数的增加而增加。(2)两台设备的总可用时间槽数越少,即检查系统的产能越匮乏时,MDP预约策略相对于传统预约策略的优势越明显,医院的总收益增长率随产能的变化图(图7)也更好的证明了这一结论。其中,假设MDP预约策略能给医院带来的总收益为r1,传统预约策略下医院可获得的总收益为r2,用k来表示医院总收益增长率,则有 (9) 图6 医院总收益随产能变化图 图7 医院收益增长率随产能变化图 其他条件不变的情况下,调节住院病人的预约到达率α2,医院的总收益随α2的变化如图8所示。在系统总产能不能满足所有病人预约请求的情况下,可得出以下结论:(1)随着住院病人预约到达率的增加,MDP预约策略下医院总收益变化不大,而传统预约策略下医院总收益呈递减趋势。这是因为在产能缺乏的情况下,随着住院病人预约到达率的增加,医院会拒绝更多病人,带来拒绝成本的上升,而在MDP预约策略下,医院也将会选择服务更多综合收益较高的住院病人,从而实现了总收益的平衡。(2)随着住院病人预约到达率的增加,MDP预约策略相对于传统预约策略的收益增长率呈上升趋势(图9)。由于住院病人的综合收益高于门诊病人的综合收益(y2+c2>y1+c1),MDP预约策略会根据住院病人预约到达率的变化,调整接受某类病人的临界值,从而为后到达的、收益更高的住院病人保留产能。另一方面,住院病人的预约请求越多,先到先得的预约方式也将有可能拒绝更多后来的住院病人,带来更高的拒绝成本。 图8 医院总收益随α2变化图 图9 医院收益增长率随α2变化图 总的来看,保持其他变量不变,当每台设备的最大可用时间槽数T变化时,两种预约策略下的各项指标随总产能的变化情况如表6所示。表6中,以T=80时的各项数值作为初始基准,各项指标变化值代表下一状态在上一状态基础上的变化情况,即T=90相对于T=80的变化情况,T=100相对于T=90的变化情况,以此类推到T=130。表7为保持其他变量不变,当住院病人到达率α2变化时各项指标的变化情况。以α2=0.1时的各项数值为初始基准,类推方式与表6相同,也表示下一状态在上一状态基础上的变化情况。从表6和表7可以进一步得出结论:系统产能越匮乏、住院病人预约到达率越高的情况下,MDP预约策略相对于传统预约策略的优越性越是突出。 表6 各项指标随产能变化情况 表7 各项指标随α2变化情况 本文针对医疗检查设备的预约调度问题,提出了利用马尔可夫决策(MDP)模型来动态处理病人的预约请求,优化目标为医院在检查设备方面收益最大化。在检查设备为两台、病人被分为三类,且各类病人所需检查时间不同的情况下,结合动态规划理论,分析系统在预约周期的最优预约排程策略。通过合理设置各参数值,利用matlab软件实现多级迭代,仿真结果证明相对于传统的先到先得的预约策略,本文的预约排程策略具有一定的优越性,能使医院在检查系统方面获得更大的收益。后对模型进行敏感性分析,分别改变两台设备的最大可用时间槽数T和住院病人的预约请求到达率α2,得出结论为马尔可夫决策(MDP)模型适用于医院的预约排程问题,并且在系统产能越匮乏、住院病人预约到达率越高的情况下,该决策模型相对于传统预约策略的优越性越是突出。后续的研究工作可考虑从以下两个方面展开,一是考虑不同设备服务能力与服务效率间的区别,二是研究模型在实际决策过程中可能带来的不公平现象,可考虑在模型建立时引入公平性因素。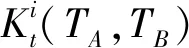
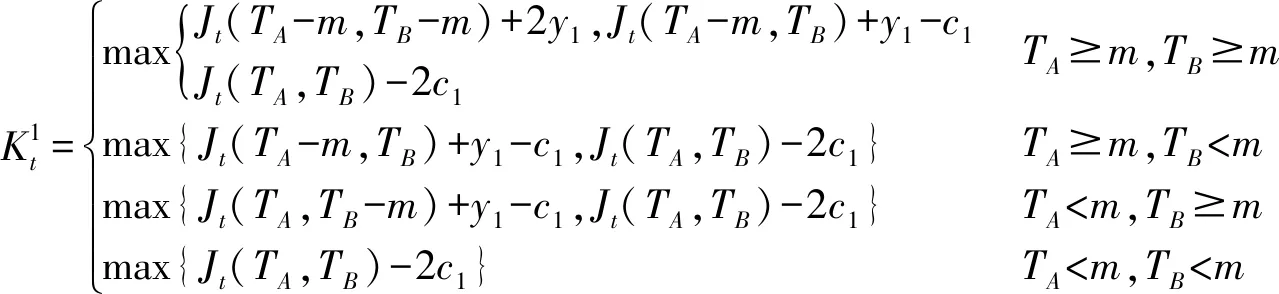
2.4 模型求解
3 数值算例


4 敏感性分析
4.1 设备的最大可用时间槽数T变化
4.2 住院病人的预约请求到达率α2变化
5 结论
