基于海空协同的群岛救援方案优化模型及算法
2020-10-24林婉妮沈铭棋宋云婷
林婉妮, 王 诺, 沈铭棋, 宋云婷
(大连海事大学 交通运输工程学院,辽宁 大连 116026)
0 引言
我国海域辽阔,海上岛屿众多,有的相互距离较远,在发生紧急情况亟需救援时,仅利用船舶救援效率过低,通常采取海空协同方式完成。但由于船舶与直升机在运载能力、驰援速度等方面的性能差异较大,相互协同救援关系复杂,因而如何有效地配置救援船舶与直升机的数量,科学地制定调度方案,是有待深入研究的重要课题。
对于远离大陆的群岛,通常将群岛中较大的岛屿作为中心岛,与周边小岛形成辐射型中心-卫星岛支撑关系。这样,以中心岛为起点,以卫星岛为终点的海空救援行动,实际上是一个带容量约束的单车场多车型最快完成车辆路径优化问题(vehicle routing problem,VRP),可以看作由中心岛(配送中心)向周边卫星岛(顾客)提供救援物资(货物),由船舶和直升机负责运送(多种车型),各船舶及直升机负责若干不同岛屿的物资配送,以实现整体配送时间最短的目标。有关车辆路径优化问题已有许多研究,例如Nikolakopoulou等人针对时间要求提出了完成时间最短的车辆路径问题,以最后一台车辆完成任务的时间最小为优化目标[1];Zhang等人研究了以平衡车辆使用时间最短为目标的车辆路径优化问题[2];丁秋雷等人研究了考虑顾客时间要求的车辆路径优化,并用混合蚁群算法对其进行求解[3];郑斌等研究了震后应急物流动态选址联运问题,并用混合遗传算法进行求解[4];王海军等针对应急物资配送选址-路径问题,建立了双目标随机规划模型,通过启发式算法来求解[5]等等。上述成果虽然考虑了带时间窗口的车辆路径优化问题,但使用的运输工具仅限于车辆,且尚未考虑节点容量和运输批次,因而并不适应本文问题,需要进行改进。
关于群岛救援也有学者做过一些研究,例如Sheller分析了2010年海地地震的重建过程,通过建立物流网络体系,探讨了海上岛屿灾后救援及物流运输过程中因孤岛运输条件限制产生的阻碍效应问题[6];Makkonen等人研究了群岛人口变化对其运输系统的影响,并以芬兰群岛为例分析了如何通过改变人口模式以及空间布局来提高群岛的运输服务水平[7];Gil等人研究了群岛之间的可持续交通规划模型,并以葡萄牙亚述尔群岛为例探讨了使用该模型解决人口可持续迁移问题的可能性[8];Shi等人以我国南沙群岛为例,分析了周边国家海上搜索和救援能力,建立了海上搜救模型,并验证其可行性[9];Hu等人针对紧急情况下的海运大批量货物的配送问题建立了开放式VRP模型和算法[10];杜永浩等人建立了多平台海上协同搜索路径优化模型,设计了多平台海上协同搜索与路径优化策略,并开展了不同规模的搜索路径优化仿真[11];佟士祺等人以轴辐式三级物流网络为基础,建立了群岛海运物流体系框架[12];吴迪等人针对边远群岛海运物流体系在构建与优化中所面对的选址-库存-路径问题,构建出物流成本最低的优化模型[13];王诺等人针对陆海联运海上战略投送过程中需解决的选址-路径优化问题,分析了陆海协同运输体系的运作机理和特点,构建了以下水港选址、运输船舶航次、航线配置以及天气条件等不确定性因素为变量、以投送时间最短为目标的选址-路径优化模型[14]等等。上述成果虽涉及了群岛运输系统以及灾后救援,但未涉及海运和空运两种方式的协同运输问题,因而还需要进行深化研究。
有关海空协同运输也有一些可供借鉴的成果,如Yang通过分析高雄市的交通需求,利用灰色预测模型预测了未来海空联运的预期运输市场[15];Menou等人探讨了摩洛哥建立海空联运中心的可能性[16];Kim和Chang分析了韩国海空联运现有模式,利用线性规划模型从环境角度讨论了海空联运的环境污染问题[17]等等。以上成果虽然考虑了海空联运的协同运输方式,但仅限于常规下的运行,并未将其作为应急救援手段,与本文问题在本质上仍有所不同。
分析发现,以上成果可为本文研究提供部分思路和借鉴,但在规划模型构建上需做进一步的深化。梳理问题可以发现,本文规划的群岛救援方案是以海空联运为背景,带容量约束的多车型多批次车辆路径问题,此类系统与传统多车型VRP问题的主要区别在于:①优化目标分为轻重缓急两类。由于救援的紧迫性,首先考虑在最短的时间内抢送关系到生存的部分药品、淡水等最急需的物资,以此作为第一个优化目标,然后再考虑如何在最短的时间内完成后续救援物资(包括抢修设备、发电机等)的运输,以此作为第二个目标;②由于救援时采用空运作业可以在短时间内完成多批次抢运,因而使得救援船舶对各岛屿的物资补给一直处于动态变化中。具体而言,由于空运具有速度快的特点,因此首轮救援主要选择直升机抢运,目标函数为抢送最急需物资的时间最短。但航空运输运量较小,送达的救援物资有限,为克服这一局限,后续救援物资的运输由直升机和救援船舶共同完成,即当直升机完成首轮物资抢送后,将继续为各受灾岛屿运送救援物资。直升机和救援船舶的运输速度相差较大,因此在救援船舶到达相应岛屿之前,直升机可能已完成对该岛屿的多次运输。在这一过程中,救援船舶因此对各岛屿的物资补给需要参考在第一轮和第二轮救援过程中各岛屿已经通过直升机运输获得的补给物资量进行综合考虑,进而对直升机和救援船舶各航次和航线的路径、运输量、运输组织形式(往返运输或循环运输)进行统筹优化,这与传统的VRP问题存在较大不同;③变量多,模型复杂。船舶与直升机在运载能力、驰援速度等方面差异较大,运行航线交错复杂,交叉联动,且各自存在往返运输与循环运输两种并行方式,需综合考虑海运和空运两种不同运输方式的特点协同组合,较传统VRP问题模型中变量更多且关系更为复杂。
综上,以上各项因素决定了群岛应急救援与传统的单批次多车型车辆路径优化问题有所不同,需要建立特定的海空协同救援模型开展研究。本文以突发事件为背景,基于需救援的岛屿数量、岛屿间距离、物资补给最小基数等要素,为制定海空协同的运输航次,编排循环或往返航线,分配机、船各航程运载量等调度策略建立相应的优化模型和求解算法,并以南海群岛的救援为实例,验证了所建模型和算法的可行性和合理性。
1 模型构建
1.1 问题分析与假设
通常情况下,针对群岛救援可供使用的应急交通工具有直升机和救援船舶两种。由于群岛距大陆较远,当突发事件发生时,可考虑以设施、设备、物资完善的中心岛屿作为基地对周边卫星岛展开救援。在直升机与救援船舶数量均有限的情况下,为了赢得时间,在制定调度方案时将采取以下做法:将救援过程分为两个并行步骤(按登岛的时间顺序将其称为首轮救援和后续救援),其中,首轮救援是指利用直升机以最快的速度为各个卫星岛抢送少量最急需的物资(如药品、淡水等)。在这一阶段中,直升机运输的组织形式包括往返运输和循环运输两种,需要根据岛屿的需求,以首轮救援时间最短为目标进行优化;后续救援包括救援船舶运输和完成首轮救援后的直升机运输两个方面,需要综合考虑救援船舶和直升机在运输能力、装卸速度和运输速度等方面的差异,以共同运输时间最短为目标,对不同运输工具的运输路线、航次数量、运输量和运输组织形式进行统筹优化。
为简化问题,假设:①中心岛储备有足够的救援物资可供调用;②所有卫星岛都处于救援船舶和直升机的航程内;③各卫星岛物资所需的最小补给基数比例相同,救援优先级相同;④直升机在中心岛的装载时间、卫星岛的卸载时间固定,救援船舶的装卸时间与装卸量有关;⑤首轮救援任务由直升机负责完成,且运载量需满足最低的需求量;⑥当直升机或船舶同一航次途经多个岛屿时,卸载量按各岛屿物资需求量等比例分配;⑦各机组以最快速度在前s个执飞航次中完成遍访各岛的首轮救援任务;⑧后续救援中,对于救援船舶已投送过的岛屿,直升机不再投送。
1.2 符号定义
设中心岛共有I架直升机,直升机的平均飞行速度为va,额定载重量为na,直升机的首轮救援时间为Z,直升机总救援时间为X;在中心岛的装载时间为te,第i架直升机的航次数量为Ji,i∈{1,2,…,I}。设中心岛共有M艘救援船舶,救援船舶完成的总救援时间为Y,救援船舶的航行速度为vb,额定载重量为nb,在中心岛的装载速度为vl,在卫星岛的卸载速度为vm,第m艘救援船的航次数量为Nm,m∈{1,2,…,M}。设共有D个卫星岛,第d个卫星岛的救援物资需求为Qd,d∈1,2,…,D,第d个卫星岛的卸载时间为td,首轮救援物资对卫星岛最小补给基数的比例为P。
对于第i架直升机的第j个航次,设路经卫星岛屿的集合为dij,路经的卫星岛上卸载的货量为Nd,d∈dij,路经中心岛到卫星岛的距离为Ld,d∈dij,路经卫星岛d与卫星岛d′之间的距离为Ldd′,d、d′∈dij,设aij、bij为0-1变量,若其航线为往返航线,则aij=1,bij=0;若为循环航线,则aij=0,bij=1;设直升机路经岛屿g救援时为Xijg,g∈{1,2,…,D},为0-1变量,若路经编号为g的岛屿,则Xijg=1,否则Xijg=0。
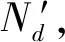
1.3 目标函数
设直升机的首轮救援时间为Z,直升机总的救援时间为X,救援船舶的总救援时间为Y,有:

(1)
(2)
m∈{1,2,…,M},n∈{1,2,…,Nm}
(3)
按照救援时间最短原则,设置目标函数如下:
Tone=min(Z)
(4)
Ttwo=min(X,Y)
(5)
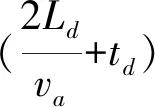
1.4 约束条件
(6)
(7)
(8)
vl·tmn≤nb,m∈{1,2,…,M},n∈{1,2,…,Nm}
(9)
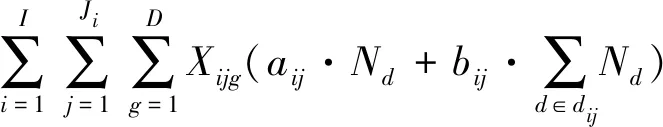
2 计算方法
由以上建模过程可知,海空协同救援路线、批量的优化实际上是一个NP-Hard问题[18],可采用启发式算法或进化算法进行求解,禁忌搜索算法、遗传算法、模拟退火算法和蚁群算法都可用于解决该类问题[19]。潘振东等采用遗传算法,提出先安排路线后分组的染色体设定方法,并设计一种基于运输点划分的遗传算法(partition based on autonomous genetic algorithm,PB-GA),该算法按照染色体上基因的顺序,依次在满足运输载体载重量的约束条件下计算每个节点费用最小的划分,并根据当前节点的最小划分对其所有后继节点的最小划分进行改进,直到得出染色体每段基因的最小划分,即整个染色体对应的可行解[20]。PB-GA算法虽然在运输节点的划分方面有所创新,但其目标函数是以成本最小为目标,且没有考虑各个运输节点的需求量,因而对本文情况并不适用。相对于传统的多车型车辆路径优化,本文所设问题与其主要差异是在考虑多批次运输的同时,还要求完成时间的最短,且只有当所有岛屿都得到所需的救援物资时整个任务才算完成。基于以上分析,本文对PB-GA算法进行进一步的改进,提出一种能够同时考虑两种运输方式、多批次运输的双层搜索遗传算法(double-deck search genetic algorithm,DS-GA)。
本文提出的DS-GA算法的核心思想是:对于任意一条染色体,首先按救援批次的先后顺序,将其划分为上层和下层两个部分,设上层为首轮救援,下层为后续救援,基于上层和下层使用的运输工具,按其数量划分为不同长度的信息段,每个信息段表示1个航次。根据需救援岛屿的数量、与中心岛的距离以及投入救援的物资量,对上层染色体进行初始化配置,使其先满足首轮救援任务,得到上层的初始可行解。然后,再对下层染色体进行搜索,根据其在运量、运输距离以及运输路线之间的复杂关系,对直升机和救援船舶同时进行配置,找到下层的可行解。基于该可行解,再对上层染色体的约束域进行划分,并开展搜索,找到上层新一轮的最优解,如此反复交互,直到上层和下层的约束域都唯一时,跳出循环结束,得出优化结果。由于染色体信息庞大,且有小数(由装卸量引起)存在,所以不做编码、解码处理,得到的初始可行解直接按式(4)、(5)进行适值计算,并完成后续的选择、变异和交叉操作。
2.1 染色体设计
为表达不同运输方式各航次、航线配置以及运载量,满足染色体序列能够完整表达全部解空间(极限情况下所有航次都为往返航线)的要求完成划分阶段操作。先将染色体分为两层,上层为首轮(由直升机执行)救援目标函数,下层为后续救援(由救援船舶和完成首轮救援的直升机共同执行)目标函数。对上、下层的染色体按各层涉及的交通工具数量、航次数量设置分隔符,两个分隔符之间的连续基因即表示某艘船或某架飞机1个航次依次经过的岛屿。此外,考虑到直升机与救援船舶不同的运载能力,每架直升机每航次单位染色体的长度固定为3位,第1、2位是其航线所经过的岛屿编号,若第2位编号为0,表示其航线为往返航线,第3位为固定的分隔符0;每艘救援船舶每航次单位染色体的长度固定为5位,第1位是其在中心岛的装载时间,第2、3、4位是其航线访问岛屿的顺序编号,若第4位编号为0,表示只经过两个岛,若第3、4位都为0,表示为往返航线,第5位是固定的分隔符0。为方便计算,不对每个航次航线上各个岛屿的卸载量以染色体表达,而是将其作为隐形条件,由其航线上的岛屿编号决定,按岛屿所需要的救援物资比例分配。例如,当有7个卫星岛需要救援时,出动救援直升机为2架,每架执飞4个航次;救援船舶为2艘,每艘救援船舶出海1个航次,按照上述规则进行初始配置,生成的染色体表达式如图1所示。

图1 染色体表达式
在图1(a)中,表示直升机执飞的前2个航次,以该染色体的前6位为例,第1~3位染色体表示机组执飞的第1个航次为循环航线,其救援路线为中心岛→4#岛屿→5#岛屿,第4~6位染色体表示机组执飞的第1个航次也为循环航线,其救援路线为中心岛→1#岛屿→6#岛屿。图1(b)表示救援船舶的运输航次以及直升机执飞的后2个航次,以前5位为例,该段染色体表示救援船舶Ⅰ在中心岛的装载时间为2.3h,只出海1个航次,其方式为循环航线,救援路线为中心岛→4#岛屿→7#岛屿→2#岛屿。
得到上述救援路线方案后,便可对各路线的配载量进行计算,相应的规则如下:①当直升机或者船舶同一航次途经多个岛屿时,在各个岛屿上的卸载量按各岛屿最小补给基数等比例分配;②当按上述比例分配无法满足个别岛屿的最低需求量或最小补给基数时,需进行邻域搜索,在航线上选择超出最低需求量或最小补给基数比例最大的岛屿,将该岛屿的卸载量降至满足条件的最小值,依次调整不满足要求的岛屿卸载量,直至所有被救援的岛屿都满足需求为止。
2.2 交叉与变异算子设计
根据染色体编码的特点,DS-GA以救援船舶装卸时间和航次岛屿号分别交叉的方式进行交叉运算,对于救援船舶单航次情况,其子代继承了父代1的装卸时间和父代2的路经岛屿顺序;对于直升机单航次情况,其子代按顺序依次继承父代1和父代2路经岛屿的顺序。具体交叉操作如图2所示。
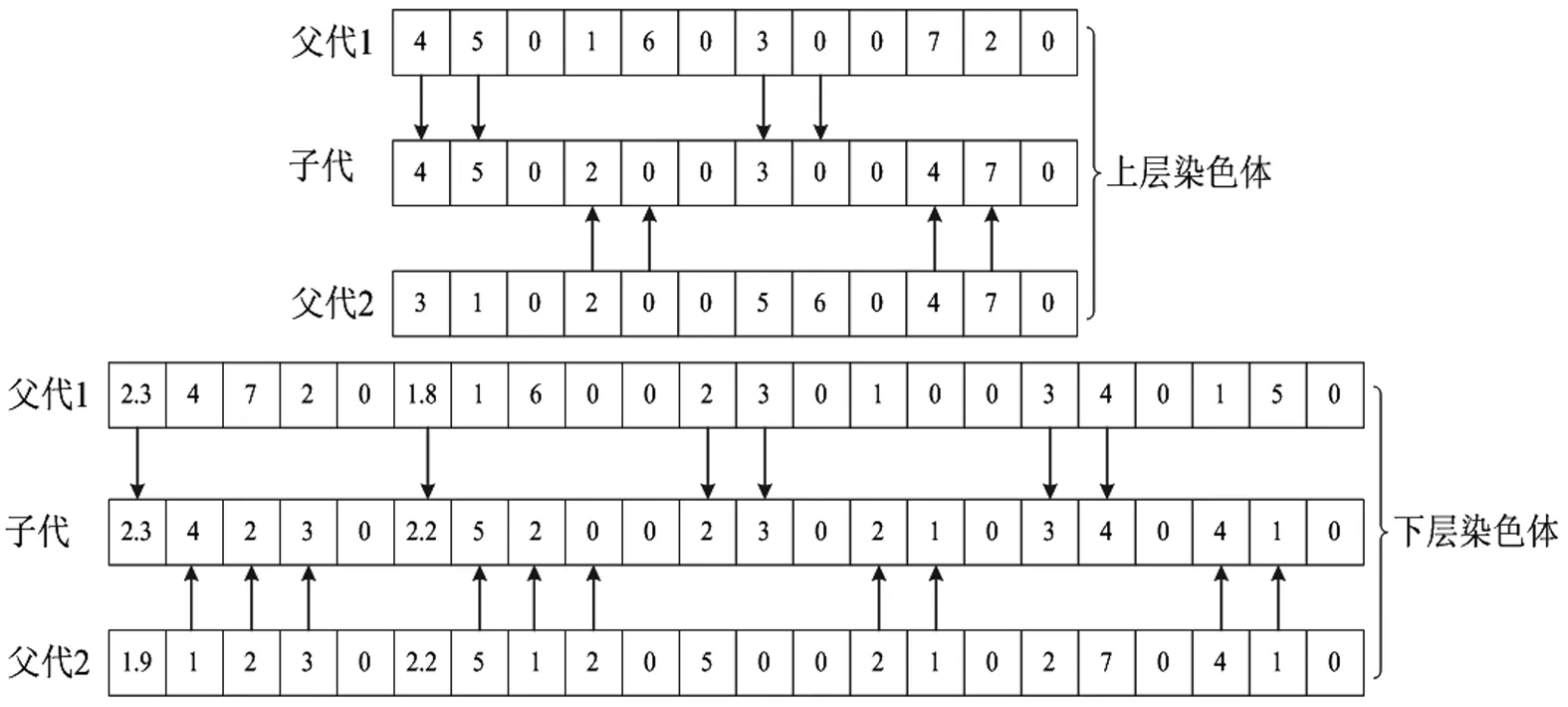
图2 交叉算子
当岛屿数量较多时,各卫星岛需要救援的物资量总和增大,需要的救援航次也增多,因此染色体将较长,包含信息也较多。为求解较为复杂的染色体,可将变异算子分为两种情况:第1种是相同运输工具不同航次间岛屿编号的交换,第2种是单独染色体某1位(除分隔符)的变异,具体操作过程如图3所示,具体流程见图4。

图3 变异算子

图4 计算流程示意图
3 算例
3.1 基本数据
现以我国南海部分岛屿为例,假定需救援的岛屿共有9个,各岛屿位置及坐标分别如图5和表1所示。设可调用直升机5架,最大载重量5t,在卫星岛的装载和卸载时间均为0.5h,最大续航时间为2.5h,平均飞行速度为260km/h(约合140n mile/h);调用救援船舶3艘,载重量200t,航速12节,在中心岛的装载速度为60t/h,在卫星岛的卸载速度为50t/h。各卫星岛物资所需最小补给基数Qd如表2所示,首轮救援物资量设定为各卫星岛物资最小补给基数的5%。
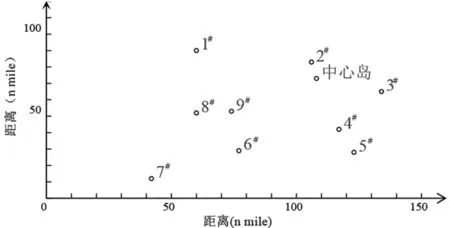
图5 某群岛各岛屿分布位置示意图

表1 各岛屿坐标(单位:n mile)

表2 各卫星岛物资补给最小基数(t)
3.2 计算结果
采用MATLAB 6.5运行DS-GA算法,设置种群个数N=30,交叉概率Nc=0.5,变异概率Nm=0.005,在windows XP,AMD Anthon(tm) Ⅱ X2 240 Processor 2.81Ghz,2GB内存的环境下完成计算。迭代3275次后得到最优解,收敛过程如图6所示。运行计算程序10次,得到首轮救援和全部完成救援的平均时间分别为3.65h、15.63h,对应的路径方案和所需时间见表3、表4和图7和图8。

图6 计算收敛过程示意图

表3 直升机救援运行方案

表4 救援船舶运行方案

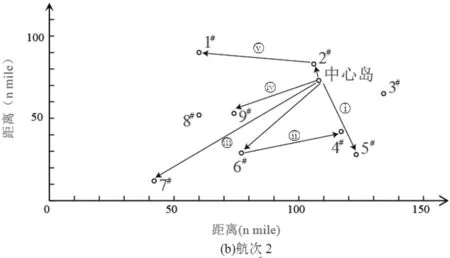
图7 首轮救援直升机飞行路线
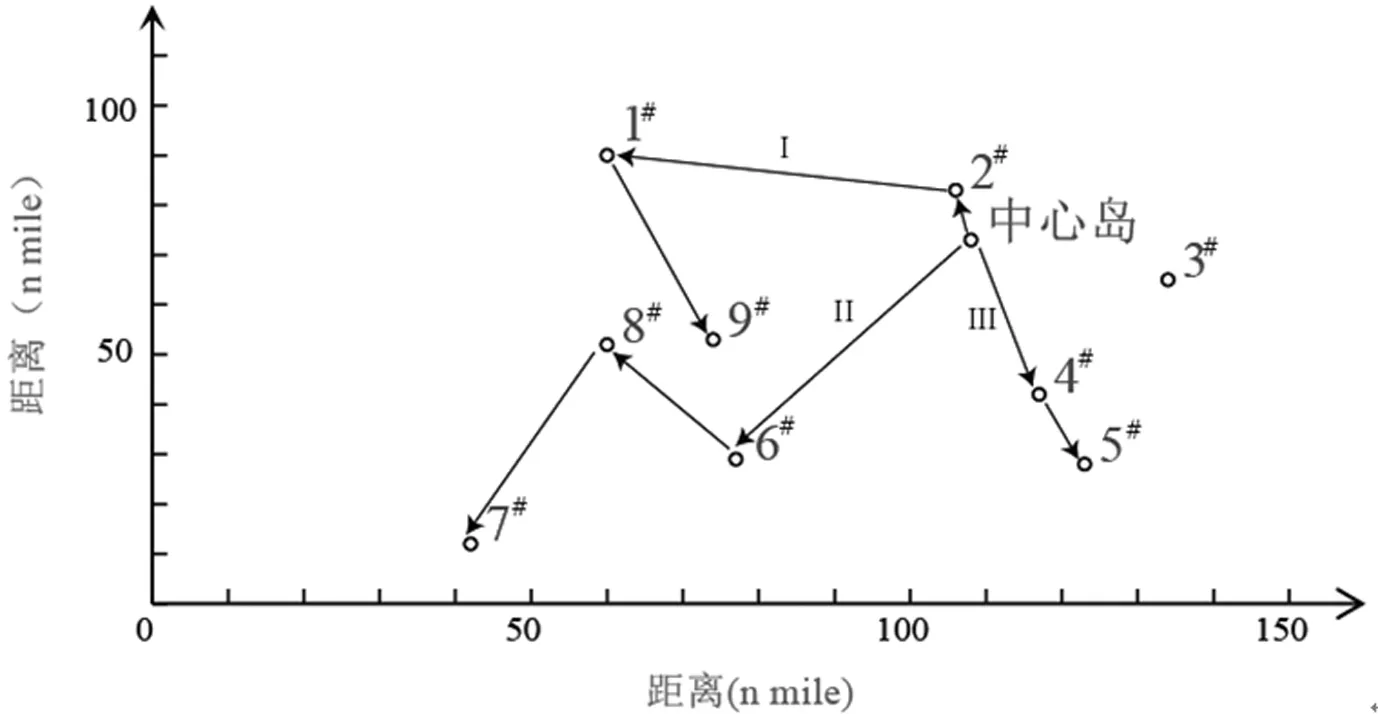
图8 船舶救援航线
3.3 算法对比
为说明本文算法的有效性,分别采用基于运输点划分的遗传算法(PB-GA)和CPLEX软件计算的精确解进行对比,对比实验仍在相同的计算机上运行,各计算10次。结果显示,在优化结果上,本文算法得到的平均救援时间为15.63h,相对于PB-GA算法的16.88h缩短了7.30%,与CPLEX求解出的结果一致,表明本文算法能够较好地找到满意解。在计算时间上,本文算法仅用时19.21s,比PB-GA算法用时21.56s缩短了11.32%,比CPLEX计算用时583s缩短了96.7%,说明本文算法具有更好的计算效率。在物理内存占用上,本文算法占用2587MB,比PB-GA算法和CPLEX计算分别减少了2.63%和5.34%。以上对比说明,本文算法能够快速收敛并得到较好结果,具体见表5。

表5 算法对比结果
4 结论
海空协同对边远群岛开展救援是最有效的一种方式,但已有研究涉及此类问题的还较少。由于救援的紧迫性,通常先要考虑在最短的时间内抢送关系到生存的部分药品、淡水等最急需的物资,然后再考虑如何在最短的时间内完成后续救援,因此整个救援实际上具有分阶段的特点。空运救援速度快,但运量小,船舶救援运量大,但速度慢,在救援船舶到达相应岛屿之前,直升机可能已完成对岛屿的多次运输。船舶与直升机在运载能力、驰援速度等方面存在巨大差异,协同时运行航线交错复杂,交叉联动,因而较传统的VRP问题更为复杂,需要建立新的规划模型和求解方法。
为解决以上问题,本文给出了海空协同救援的调度方案优化模型,提出双层搜索遗传算法(DS-GA),并结合算例进行了求解,得到了较为理想的优化效果,表明本文所建模型及算法是合理有效的,可为我国有关部门制定救援方案提供借鉴。
需要指出,本文仅以同一群岛的中心岛对各卫星岛展开救援为研究背景,而当面对多组群岛,或有的救援物资需从大陆紧急调拨时,其调度计划将会变得更为复杂,对于此类问题如何构建优化模型,是下一步需要深入研究的内容。
