鲁棒动态设施选址问题的近似算法
2020-10-24吴晨晨徐春明徐大川
吴晨晨, 王 丽, 徐春明, 徐大川
(1.南开大学 商学院,天津 300371; 2.天津理工大学 理学院,天津 300384; 3.北京工业大学 数学学院,北京 100124)
0 引言
在建立和管理实体企业中,首要任务就是要进行合理的选址。同时,选址也是事业扩展的第一步。因此设施选址的重要性显而易见。另一方面,设施是指在生成过程赖以运行的硬件条件,常见由工厂、仓库、车间等实体构成。而设施选址就是指合理利用科学方法选择以上提及设施的地理位置,使其与企业整体运营体系有机结合,从而达到企业的经营目标。选址后对建成后的设施布置以及投产后的生产经营费用、产品和服务质量以及成本都有极大而长久的影响。考虑到不当的设施选址会给企业运营带来若干不良影响,而仅靠事后加强和完善管理是无法弥补的,因此该问题引起了众多学者的关注[21]。 在进行设施选址时,必须充分考虑到多方面因素的影响,慎重决策。除新建企业的设施选址问题以外,随着经济的发展,城市规模的扩大,以及地区之间的发展差异,很多企业面临着重新选址的问题,等等。可见,设施选址是很多企业在生产运作过程中都面临的一个重要问题。大量的成功案例证明,在选址问题上,以下原则是必要的。
(1)成本最小原则:作为经济实体的企业,经济利益对于企业无论何时何地都是重要的。固定费用,单个顾客的服务成本,等等都与选址有关。
(2)接近顾客原则:对于实体经济,都需要遵循这条原则,如银行储蓄所、邮电局、电影院、医院、学校、零售业的所有商店等。许多制造企业也把工厂建到消费市场附近,以降低运费和损耗。
(3)动态发展原则:选址是一项带有战略性的经营管理活动,因此在选址是要综合考虑企业生产力的合理布局,市场的开拓。这样才能在当前世界经济越来越趋于一体化的时代背景下,增加企业的竞争力。
从解决问题的角度看,设施选址问题是起源于传统韦伯问题 (Weber Problem)。具体地说,该问题是指在待选的地址中开设一个设施,使得事先给定的顾客连接到该设施的距离之和最小。对于此类问题只需事先将所有待选设施中的所有设施遍历计算相应的费用得到最小的决策即为最优解。随着社会和经济发展,开设一个设施远远不够,同时设施的建立也需要一定的成本。由此,不断发展出了设施选址问题,其中最经典的问题为无容量的设施选址问题 (uncapacitated facility location problem,简称UFLP)。
无容量设施选址问题是指给定设施的集合F和顾客的集合C,设施i∈F的开设费用为fi,设施i∈F和顾客j∈C之间的连接费用(即服务成本)为cij,该问题的目标为开设一些设施,将每个顾客连接到一个开设的设施 上使得开设费用和连接费用之和最小。由于可以从集合覆盖问题规约而来,从而设施选址问题是NP-困难的。这类问题在P≠NP的假设下,不存在有效时间的 (即多项式时间)算法。为此,处理这类问题的一个重要方法是丢弃掉对最优解的追求,找到问题的一个可控的可行解即可。这类方法称为近似算法,即,如果算法A所得解的费用不超过α倍最优值,那么被称为α-近似算法。UFLP的第一个常数近似比是由Shmoys等人[18]通过建立整数线性规划,松弛整数约束,进而利用算法将分数最优解舍入为整数解,给出了3.16-近似算法。后来,许多学者不断创造新的技巧得到更好的近似比。总体来说,设施选址问题的近似算法技巧可以分为四类,线性规划舍入[18],原始-对偶[11],对偶-拟合[10],局部搜索[1]。目前,最好的近似比是Li[15]利用综合线性规划舍入和对偶-拟合技巧得到的1.488-近似算法。除非P=NP,UFLP不存在近似比低于1.463的近似算法[6]。
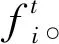
在设施建立后服务顾客的过程中,有时会遇到某些顾客的服务成本很高的情形。因此,经常在此类问题中加入一些鲁棒设置。这里介绍两种。第一种,每个顾客都有不被服务的成本,这里称之为惩罚费用。若选择不服务该顾客,则需要支付相应的惩罚费用,这类问题则称之为带惩罚的设施选址问题(facility location problem with penalties,简称FLPWP)。第二种,规定可以至多不服务个顾客,这些顾客被称为异常点(outlier)。允许异常点的设施选址问题被称为带异常点的设施选址问题(facility location problem with outliers,简称FLPWO)。
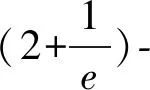
优化问题中,时常考虑异常点的设置。FLPWO由Charikar等[2]提出,在设施选址问题原始对偶技巧的基础上得到3-近似算法。此外,异常点设置在数据挖掘中有重要的应用。Gupta等[7]利用局部搜索技巧得到了常数的近似比,但会较小的违背异常点数目限制。在此之后,不断有学者对此问题进行讨论[3,5,7,14]。
对比前述工作,本文将讨论同时具有带惩罚和异常点的动态设施选址问题(dynamic facility location problem with penalties and outliers,简称DFLPWPO),利用原始对偶技巧,保持了近似比,得到3-近似算法。本文接下来将按照如下结构对鲁棒动态设施选址问题的研究工作展开论述。第二部分将介绍鲁棒动态设施选址问题的描述和相关的符号;第三部分将介绍原始-对偶算法;第四部分将对第二部分的算法进行分析,得到近似比为3;最后则对全文进行总结并给出研究展望。
1 问题描述与符号
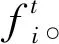
为了方便描述问题和设计算法,本文引入以下概念和相关记号:
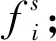
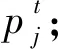
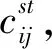
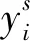
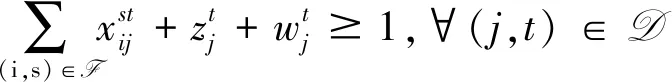
∀(i,s)∈F,(j,t)∈D
(1)
在上述规划中,第一组约束表示每个顾客-时刻对(j,t)要不连接到一个设施-时刻对,要不被惩罚,要不作为异常点;第二组约束表示如果顾客-时刻对(j,t)连接到设施-时刻对(i,s)上,则设施-时刻对一定开设;第三组约束表示异常点至多有l个。
2 算法
由于FLPWO的整数间隙是无穷,从而作为推广模型的DFLPWPO,其整数间隙也为无穷。为处理这一问题个算法设计带来的困难,我们借助文献[2]中转变实例的方法。因此,对于给定DFLPWPO的实例I,我们将其转化为实例I′。具体转化过程为,记(ih,sh)是最优解中开设费用最大的设施-时刻对。重新定义设施费用
因此,实例I′的整数规划为:
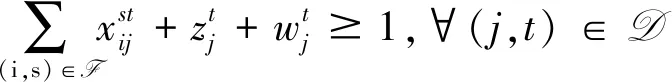
∀(i,s)∈F,(j,t)∈D
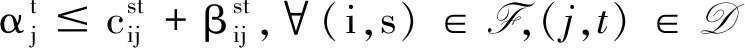
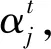
算法1
步骤0初始时,设置
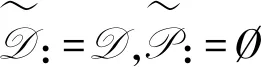
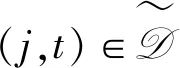
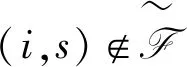
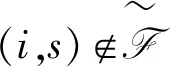
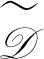
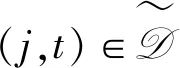
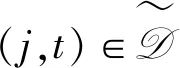
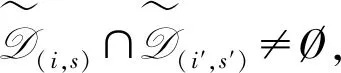
3 分析
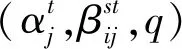
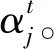
接下来我们分别分析顾客的连接费用和惩罚费用。
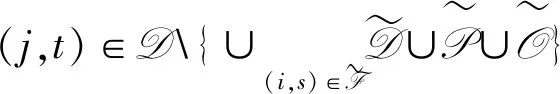
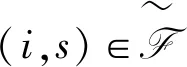
根据三角不等式,有
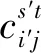
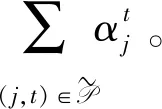
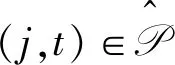
综合以上引理,可以得到算法的近似比。
定理4.4算法1是DFLPWPO的3-近似算法。
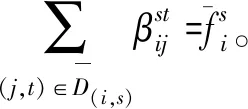
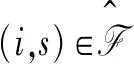
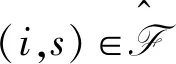
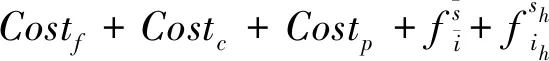
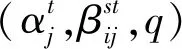
4 总结和展望
本文主要讨论了鲁棒动态设施选址问题,将带惩罚和带异常点两种变形嵌入到动态设施选址问题中,利用原始-对偶的基本框架设计得到3-近似算法。在设施选址问题仍有待解决的问题, 其中无容量设施选址问题的突破近似比上界(1.488)和近似比下界(1.463)之间的壁垒是近似算法领域里最有趣的问题之一。 此外, 是否存在基于局部搜索框架的带异常点的设施选址问题的近似算法也是有意义的问题。
