梯形波纹腹板钢梁有限元优化分析

2020-10-24罗洪光张婵韬蔡诚秀

湖南工程学院学报（自然科学版） 2020年3期

关键词：钢梁腹板屈曲

罗洪光，张婵韬，蔡诚秀

（湖南工程学院建筑工程学院，湘潭411104）

1 概述

由于波纹腹板具备合理的受力性能，波纹腹板钢梁得到广泛应用［1-2］.

梯形波纹腹板构形及有关几何参数如图1所示.

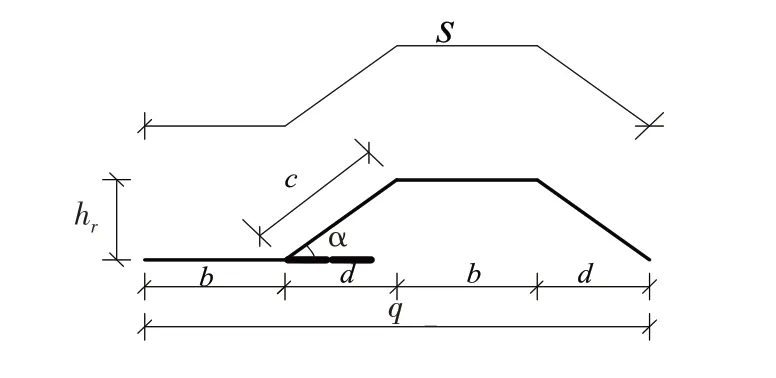
图1 梯形波纹腹板构形及几何参数

由于存在“手风琴效应”，波纹腹板钢梁剪力主要由腹板承担，弯矩主要由翼缘承担［3-4］.“手风琴效应”为计算带来简便，并被纳入相关设计规范［2］.B.Kövesdi 等［5］指出可利用有限元方法精确计算波纹腹板钢梁.罗洪光等［6］运用有限元对梯形波纹腹板钢梁设计参数进行优化分析.

本文拟针对常见的跨中集中荷载作用下的简支梯形波纹腹板钢梁，在弹性范围内运用通用有限元程序ANSYS［7］对钢梁开展多个设计变量的优化分析，并与平腹板钢梁优化对比，揭示梯形波纹腹板钢梁承载特点，推进梯形波纹腹板钢梁计算与设计.

2 有限元建模

本文计算首选梯形波纹腹板钢梁试件设计变量为：hr=50 mm，d =50 mm，b=70 mm，腹板高度hw=500 mm，腹板厚度tw=3 mm，翼缘厚度tf=12 mm，翼缘宽度bf=250 mm.

图2 所示梯形波纹腹板钢梁跨中承受荷载2Fy作用，其几何与荷载条件均为最不利情形［5］，［8］.图2 所示的钢梁计算模型如图3 所示，在图3 所示荷载条件下，本文计算取Fy=100 kN.

图2 梯形波纹腹板钢梁

图3 梯形波纹腹板钢梁计算模型

本文采用ANSYS 三维壳单元Shell93 进行建模，弹性模量E 取210 GPa，泊松比ν 取0.3.针对简支钢梁建模分析，支座及加载位置均对称设置加劲肋.

3 有限元优化

本文选择梯形波纹腹板钢梁的7 个几何参数hr、b、d、tw、tf、bf和hw作为优化设计变量.

设不考虑腹板的抗弯性能条件下的翼缘平均弯曲正应力为σ'x，σ'x大小与L 有关，为便于对比，在计算σ'x时，本文统一选取L=4 m.由于对称性，本文采用半跨梁建模，支座端部位置处，腹板起始点位于翼缘中部，如图2 所示.为了保证腹板板段的完整性，令实际半跨长度不小于2 m，且0.5L-2 m不大于0.5b 或0.5d.

在梯形波纹腹板钢梁弹性抗弯强度计算中，需考虑翼缘横向弯矩的影响［9］，翼缘最大横向弯矩可采用式（1）进行计算.

式中，V 为计算截面剪力.

与My,max对应的最大正应力位于翼缘端部，则σ'x与（设二者为同号应力）叠加值σx相对较大.

本文选择τxy、第一阶屈曲系数k 以及σx作为状态变量.

给设计变量定义一个合理的取值范围有利于计算效率的提高［10］.本文设计变量hr上下限设为200 mm 和20 mm、设计变量d 和b 取值上下限均设为300 mm 和20 mm，设计变量tw取值下上限设为2 mm 和10 mm，tf取值下上限设为4 mm 和16 mm，bf取值下上限设为200 mm 和600 mm，hw取值下上限设为300 mm 和1500 mm.本文钢梁采用Q235 钢，为充分利用钢梁抗剪和抗弯强度，状态变量τxy和σx设定取值上限分别为125 MPa、215 MPa.考虑钢梁的稳定承载力不低于强度承载力的要求，状态变量k 设定取值下限为1.

为实现计算的可对比性，本文将钢梁单位长度体积2V/L 作为目标变量，其中V 为半跨钢梁体积，不含加劲肋体积.

首先运行随机搜索，可以删除那些不合理的设计序列［11］.因此本文采用随机搜索法对应命令“optype，grad”开展优化计算，并运用“opsel，-1”删除不可行设计，利用“opsel，n”命令选择n 个较优的可行设计，提高后续计算的运行效率.

零阶方法是通用的ANSYS 优化方法，可以有效地处理绝大多数的工程问题［12］，本文采用零阶方法进行优化计算.同样，在前一轮零阶方法计算结果基础上，利用“opsel，n”命令选择n 个较优的可行设计，提高后一轮零阶方法计算的运行效率.

零阶方法在多重优化方法中较为关键，进行若干轮零阶方法计算，可逐步逼近优化值.因此，运用ANSYS 参数化设计语言APDL，预设循环次数和目标变量值，利用零阶方法进行循环优化计算，利于实现优化目的.

随着向最优点的靠近，优化进展变得较为缓慢［13］.一般情况下，后一轮零阶方法计算得到新的较优设计，随着零阶方法计算轮数的增加，后续零阶方法较优设计目标变量计算值变化较小.

此外，为了尽量获取全局最优解，当前后2 轮零阶方法较优设计目标变量计算值比较接近时，本文再运用扫描法对整个设计空间进行等步长的扫描.

本文运用“opsweep”命令指定控制点和评估点个数，并及时运用“opsel，-1”和“opsel，n”命令选择合适的可行设计集，提高后续计算效率.

前一轮多重优化结束后，再依次运用随机搜索法、零阶方法、扫描法开展新一轮的优化计算过程，直至前后2 轮优化目标变量接近为止.经过上述若干轮多重优化，目标变量2V/L 的迭代曲线如图4所示，其中横坐标为设计集序号，纵坐标为目标变量计算值.本文迭代曲线对应的设计集均为可行设计集.需指出的是，在图4 基础上，还存在进一步优化的可能.但在实际工程结构优化时，工程师追求的并不是一个精确的最优解，往往只要有一个合理的精度便够了［13］.考虑到优化空间逐步变小以及计算耗时逐步增加，因此本文目的不是确定一个精确的最优解，只是求得具有一定实际应用意义的相对较优解.

图4 梯形波纹腹板钢梁目标变量2V/L的迭代曲线1

图4 中相对较优解对应的设计集序号为241，由于在优化过程中，本文仅选择若干较优设计集作为后续优化的基础，因此图4 设计集序号只包含部分较优设计集的序号.图4 相对较优解对应的目标变量2V/L = 4125.5 mm2，优化解对应的设计变量tw=2.0 mm，hr=25.7 mm，d =44.8 mm，b=90.1 mm，tf=5.3 mm，bf=218.6 mm，hw=846.1 mm，0.5L=2001.1 mm.优化解对应的剪应力τxy和正应力σx分别为88 MPa 和214 MPa. 跨中σxy和σx' 之比约为0.04，说明优化后的钢梁横向弯矩对于抗弯强度的影响并不大.第一阶屈曲系数k=1.00，如图5 所示，对应的梯形波纹腹板钢梁屈曲模式为整体屈曲.

图5 梯形波纹腹板钢梁最优解一阶屈曲z向变形图

需指出的是，为尽可能反映实际优化计算结果，上述钢梁优化解相关几何参数保留小数点后一位数值，钢材密度以7.85 t/m3进行计算（后文不作说明，均同）.图5 相对较优解对应的每米钢梁自重约为32.4 kg，而钢梁优化前对应的每米自重约为61.1 kg.优化后与优化前相比，每米钢梁材料用量减少约47%.

在求最优设计时精度不必要求很高.目前还缺少切实可行判别全局最优的方法，常用的办法是让迭代算法从几个不同的初始设计出发，从中比较出全局最优的解［13］.

本文改变首选梯形波纹腹板钢梁设计变量参数，选择以下新的设计变量：hr=100 mm、d=200 mm、b=200 mm、hw=1000 mm、tf=10 mm、tw=6 mm、bf=400 mm.对新初始设计条件下的钢梁进行优化，目标变量2V/L 的迭代曲线如图6 所示，相对较优解对应的设计集序号为244，对应的目标变量2V/L =4340.1 mm2，0.5L=2032.2 mm，第一阶屈曲系数k=1.02，类似于如图5 所示对应的屈曲模式仍为整体屈曲.优化解钢梁每米自重约为34.1 kg，与首选设计变量对应的优化解每米钢梁自重32.4 kg 相比，偏差约为5%，二者比较接近.因此通过对比，可取每米钢梁自重32.4 kg 对应的设计集作为本文梯形波纹腹板钢梁相对较优解.

图6 梯形波纹腹板钢梁目标变量2V/L的迭代曲线2

在钢梁相对较优解基础上，对有关几何参数取整，得到比较符合实际生产情况的设计变量：tw=2 mm，hr=25 mm，d=45 mm，b=90 mm，tf=6 mm，bf=220 mm，hw=850 mm.钢梁自重约为35.0 kg/m，与优化前自重61.1 kg/m 相比，每米钢梁材料用量减少约43%.0.5L=2002.5 mm，第一阶屈曲系数k=1.15，对应的屈曲模式为整体屈曲.τxy和σx分别为88 MPa 和185 MPa.跨中σyx和σ'x之比约为0.04.

对于平腹板钢梁，选择几何参数tw、tf、bf和hw作为设计变量，设计变量初始值为：tw=6 mm、tf=10 mm、bf=400 mm 和hw=1000 mm.设计变量相应的上下限与梯形波纹腹板钢梁相同，状态变量、目标变量均同于梯形波纹腹板钢梁.按上述多重优化得目标变量2V/L 的迭代曲线如图7 所示.

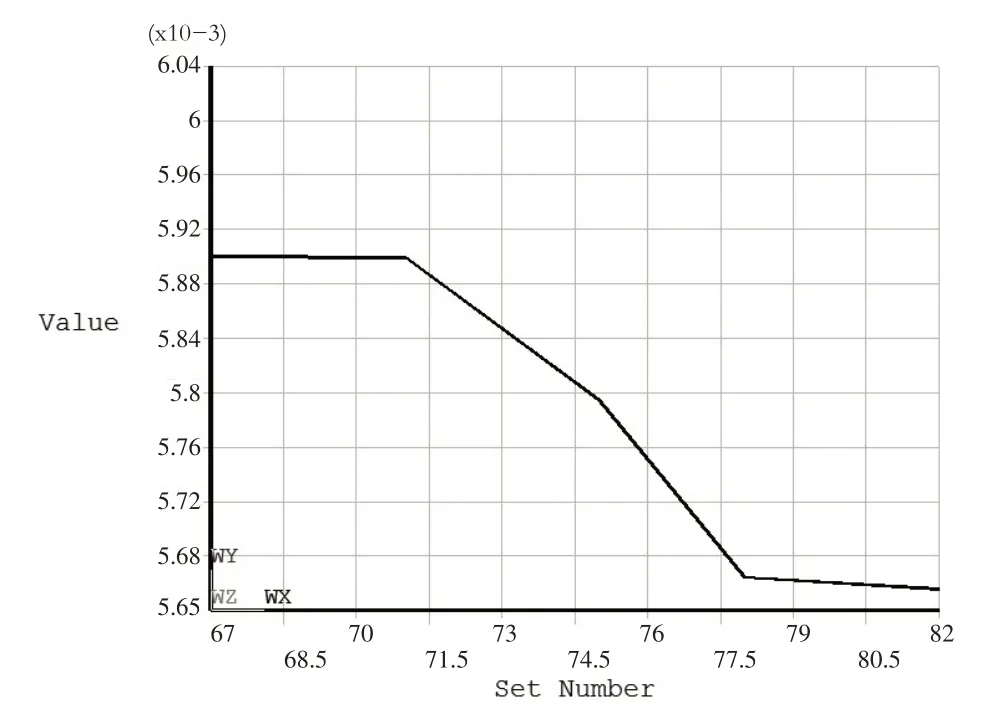
图7 平腹板钢梁目标变量2V/L的迭代曲线

图7 中相对较优解对应的设计集序号为82，平腹板钢梁较优解自重约为44.4 kg/m，与优化前钢梁自重110.8 kg/m 相比，每米钢梁材料用量减少约66%.平腹板钢梁较优解主要几何参数为：hw=424.5 mm、tw=4.1 mm、tf=7.8 mm、bf=250.0 mm、0.5L=2000.0 mm，剪应力τxy和正应力σx分别为100 MPa 和211 MPa，第一阶屈曲系数k=1.00，对应的屈曲模式如图8 所示，表现为整体屈曲.

图8 平腹板钢梁最优解一阶屈曲z向变形图

经过优化，梯形波纹腹板钢梁与平腹板钢梁的τxy、σx均接近于强度上限值，第一阶屈曲系数均接近于1，这表明优化后的钢梁抗弯、抗剪以及屈曲承载力均比较相近.与优化前对比，优化后钢梁自重下降显著，符合优化目标.

就本文所选取的钢梁优化而言，与梯形波纹腹板钢梁优化解相比，平腹板钢梁优化解每米自重增加约37%，自重增加的主要因素在于板件厚度较大，其中平腹板钢梁优化解腹板厚度约为梯形波纹腹板钢梁优化解腹板厚度的2 倍.腹板厚度与钢梁抗剪强度与腹板局部屈曲有关，这反映出与平腹板钢梁相比，梯形波纹腹板钢梁在腹板抗剪承载力方面具有一定程度的优势.另一方面，与梯形波纹腹板钢梁优化解相比，平腹板钢梁优化解梁高约为前者的50%，这主要是由于梯形波纹腹板钢梁存在“手风琴”效应，腹板抗弯性能忽略不计的原因，从该角度而言，平腹板钢梁在抗弯性能方面具有一定的优势.本文两类钢梁优化解的对比展现了两类钢梁在抗剪和抗弯性能方面的主要特点.