反复应力松弛下黄麻织物/聚乙烯复合材料的变形特性

汪泽幸，吴 波，李 帅，何 斌

（湖南工程学院 纺织服装学院，湘潭411104）

0 引言

作为一种来源极其广泛、最具发展前景的生物质材料，麻纤维具有高产、低密、易降解、力学性能优异等优点，在诸如聚乙烯（Polyethylene，PE）、聚丙烯（Polypropylene，PP）、聚乳酸（Polylactic acid，PLA）、热塑性淀粉（Thermoplastic Starch，TPS）等热塑性塑料的增强改性方面应用广泛［1-3］.

为全面研究麻纤维增强热塑性复合材料的力学行为，众多学者就麻纤维增强热塑性复合材料制备工艺对麻纤维增强热塑性复合材料拉伸［2，5-7］、抗冲击［5-7］、弯曲［4-8］、蠕变［9-12］、应力松弛［12］以及动态力学性能［9］的影响进行了研究.此外，Berhanu［13］就液态环境介质对麻纤维增强聚丙烯复合材料的耐老化性能进行了分析，文献［14］分析了循环加载下麻纤维/聚乙烯复合材料的变形特征与能量耗散特性.但少有学者对其在复杂受力条件下的行为特性进行研究.

为进一步研究复杂受力条件下麻纤维增强热塑性复合材料的变形特性，本文以黄麻织物/聚乙烯复合材料为研究对象，分析循环加载条件下应力松弛对材料变形特性的影响.

1 试样制备与试验方法

1.1 试样制备

增强体为黄麻织物，组织结构为平纹，经、纬纱均为240 tex，经、纬向纱线排列密度为（68×58）根/10 cm，单位面积质量为315.6 g/m2.

热压制备黄麻/聚乙烯复合材料前，将黄麻织物在90 ℃条件下烘干2 h，以充分去除黄麻织物中的水分.采用自行搭建的热压设备制备热塑性复合材料，单层黄麻织物双面铺设厚度为0.50 mm 的聚乙烯膜，160 ℃下预热15 min，1 MPa 热压压力条件下保压15 min 后在保压条件下自然冷却，获得黄麻织物/聚乙烯复合材料，实测成品厚度为1.60 mm.

沿黄麻织物经纬向制备矩形试样，试样宽为25 mm，长为200 mm，有效夹持隔距为100 mm.

1.2 试验方法

在WDW-20C 微机控制电子万能试验机上自动进行加载-应力松弛-卸载-应力松弛循环，设计实验过程为：以1 mm/min 加载速率加载至循环峰值应力σmax并保持应变trs，即应力松弛trs，后以1 mm/min 的速率卸载至循环下限应力σmin，并保持应变trs，设定循环次数N 为30 次.为确保循环实验过程中试样处于拉伸状态，各次循环的下限应力σmin设定为0.8 N/mm2.由于经纬向试样在反复应力松弛下的力学行为特性相似，故本文仅对经向试样进行测试和分析.

所有实验均在环境温度为（20±1）℃、相对湿度为（65±2）%的条件下进行.

2 试验结果与分析

2.1 应力应变曲线特征

4 种应力松弛时间和3 种循环应力峰值下30 次循环松弛过程的应力-应变曲线如图1 所示.从图中可以看出，黄麻织物增强聚乙烯复合材料为典型的非弹性材料.反复应力松弛条件下各循环曲线的几何形态高度相似，表明反复应力松弛下材料的变形机理是一致的.

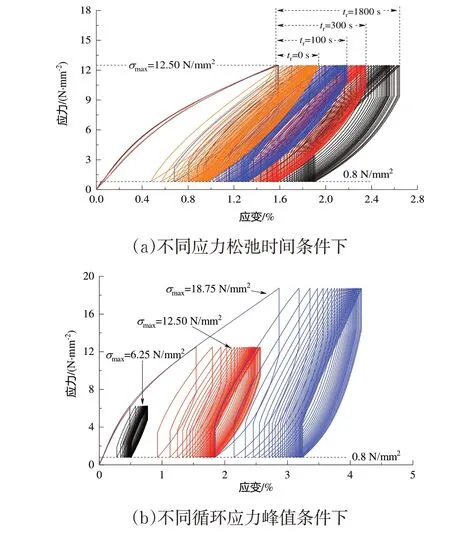
图1 试样应力应变曲线

如图1 所示，同种实验条件下各循环曲线具有较好的相似性，第1 次和第2 次循环曲线之间存在明显的差异性，所表现出的差异性随循环峰值应力提高和应力松弛时间的增加而表现得更加明显.同等实验条件下，随着循环次数的增加，相邻2 次的循环曲线之间的差异性逐渐减少，并呈现重合的趋势.从而表明，循环曲线的形态由循环峰值应力、应力松弛时间和循环次数共同决定.

2.2 最大应变量与最小应变量

各循环加载至峰值应力时的最大应变εmax以及卸载至下限应力时的最小应变εmin的获取方法如图2 所示.

图2 最大应变量与最小应变量的确定方法

本文实验条件下，黄麻织物/聚乙烯复合材料各循环的最大应变量以及最小应变量曲线绘于图3中.从图3 中可以看出，随循环次数的增加，各循环的最大应变与最小应变均呈现先快后慢的增加趋势.同等实验条件下，随应力松弛时间的增加，各循环的最大应变（N≥2 时）与最小应变均随之增加；随循环峰值应力的提高，各循环的最大应变与最小应变亦表现相似的变化趋势.

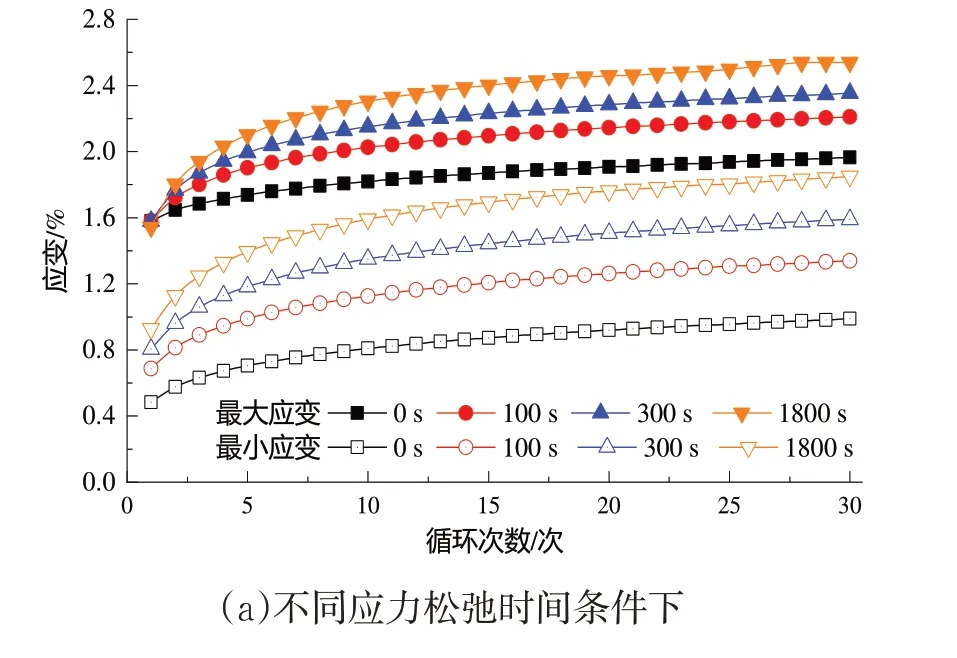
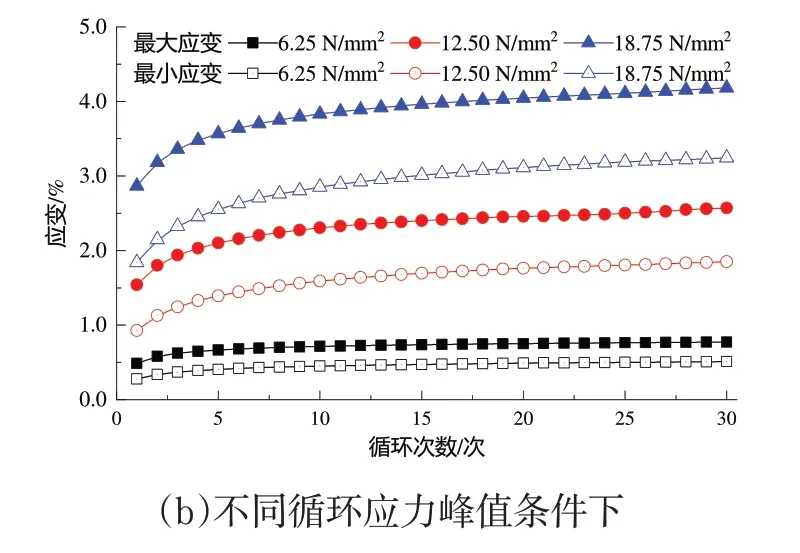
图3 最大应变量与最小应变曲线

2.3 各循环加载应变与残余应变

循环峰值应力为12.5 N/mm2，应力松弛时间分别为0、100、300 与1800 s 时各循环的加载应变与残余应变绘于图4 中.应力松弛时间为1800 s，循环峰值应力分别为6.25、12.50 以及18.75 N/mm2时，各循环的加载应变与残余应变绘于图5 中.

图4 表明，同等循环峰值应力时，随应力松弛时间的增加，各循环的加载应变（i ≥2 时）随之减少，各循环的残余应变随之增加，且均随循环次数的增加而呈现先快后慢的减少趋势.

图4 不同应力松弛时间的加载应变与残余应变曲线图

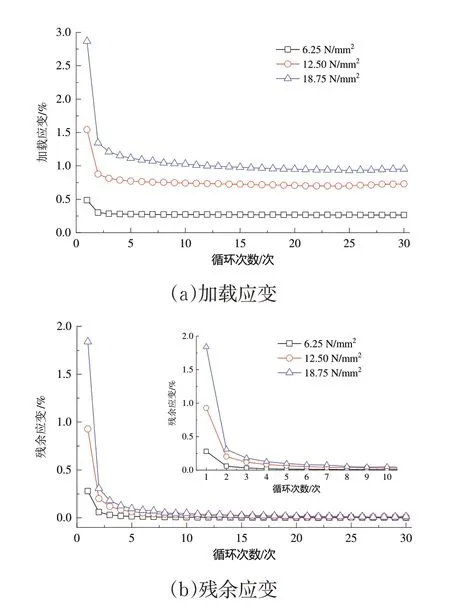
图5 不同循环应力峰值的加载应变与残余应变曲线图

从图5 中可以看出，相同应力松弛时间条件下，各循环的加载应变与残余应变随循环峰值应力的增加而增加，亦均随循环次数的增加而呈现先快后慢的减少趋势.

1 个完整的反复应力松弛循环，由加载、应力松弛、卸载、应力松弛4 个阶段构成.加载阶段，在外加载荷作用下，增强黄麻纤维和基体聚乙烯中大分子链伸直、伸长并产生滑移.同时，在外加载荷作用下，黄麻织物中纱线屈曲结构发生变化并产生伸长.同等循环峰值应力条件下，因试样中纱线力学性能存在非均匀特性以及试样宽度之间存在差异，故在首个应力松弛循环（i =1）中，当试样加载至设定载荷时，各试样产生的变形（即第1 个循环的加载应变）存在小幅度差异，但差异并不显著.应力松弛阶段，试样变形保持，在内应力作用下，增强黄麻纤维和基体聚乙烯大分子链之间继续产生滑移并在新位置建立平衡，从而产生不可逆的残余应变；在此过程中，应力松弛时间越长，即变形保持时间越长，增强黄麻纤维和基体聚乙烯大分子链之间的滑移程度越充分，产生的残余应变量增加，材料中大分子链弹性变形量减少，后续循环加载阶段材料的变形主要为大分子链的弹性变形，从而宏观表现为随应力松弛时间增加，残余应变增加，而加载应变减少（i ≥2）.

同等应力松弛条件下，循环峰值应力增加，材料在加载阶段承受的外加载荷较高，增强黄麻织物中纱线屈曲结构改变程度较高，增强黄麻纤维和具体聚乙烯中大分子链承受的张力亦较高，导致大分子链的伸长量和滑移程度较高，从而宏观表现为加载应变随循环峰值应力的增加而增加.因加载阶段大分子链承受的张力较高，在后续应力松弛阶段，大分子链构象可调整程度较高，大分子链之间滑移程度亦较高，从而宏观表现为残余应变量较高.

随着循环加载的进行，增强黄麻纤维和基体聚乙烯大分子链中产生滑移的量逐渐减少，材料的变形主要源于大分子链的弹性变形，增强黄麻织物中纱线屈曲结构趋于稳定，从而宏观表现为随循环加载次数的增加，各循环的加载应变与残余应变均呈现逐渐减少的变化趋势.

2.4 相对残余变形指数

为表征试样在各循环的非弹性程度，特引入相对残余变形指数β，其表征同一循环中残余应变相对于加载应变的比重，其值越高，表明在此循环中残余应变的比重越高，非弹性程度越高.相对残余变形指数β 可表示为：

式中，i 为循环次数，1≤i ≤30.

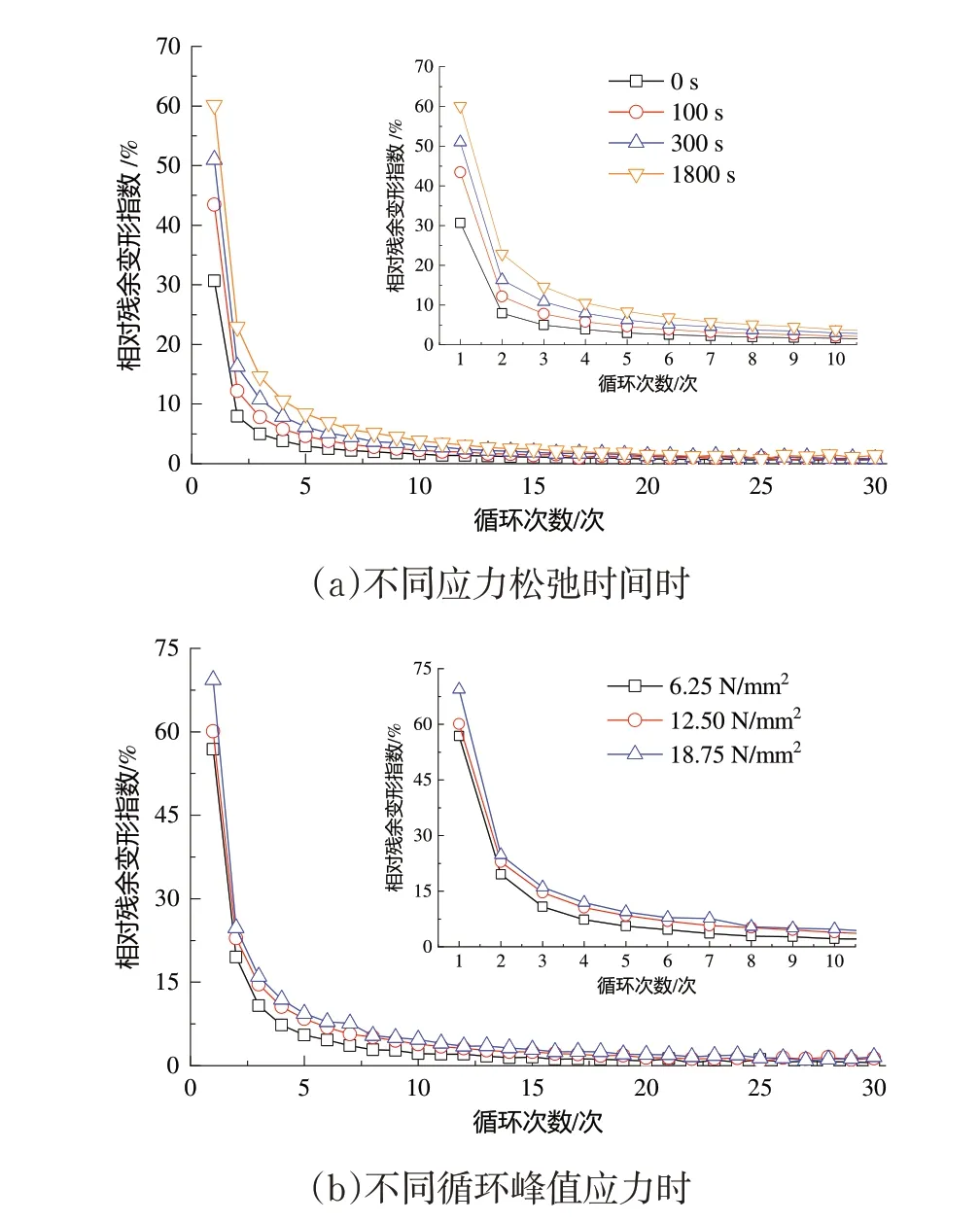
图6 相对残余变形指数

图6 示出，同等循环加载次数下，随应力松弛时间的增加和循环峰值应力的提高，黄麻织物/聚乙烯复合材料的相对残余变形指数随之增加，且均随加载次数的增加而不断减少，初始加载循环（i ≤5）时，相对残余变形指数随加载次数的变化最为明显.

相对残余变相指数产生如图6 所示的变化趋势，主要是由于随应力松弛时间的增加和循环峰值应力的增加，增强黄麻纤维和基体聚乙烯中大分子链的滑移程度越充分，塑性变形比例越高，宏观表现为相对残余变形指数随应力松弛时间的增加和循环峰值应力的提高而增加.此外，随着反复应力松弛的进行，增强黄麻纤维和基体聚乙烯中大分子链的滑移量逐渐减少，试样的变形主要为大分子键长和键角的变化，大分子链的伸长等弹性变形，从而宏观表现为，随循环加载次数的增加，材料的相对残余变形指数呈现逐渐减少的变化趋势.

3 结论

为研究复杂受力条件下，麻纤维增强热塑性复合材料的变形特性，以热压法制备黄麻/聚乙烯复合材料为研究对象，对其循环应力松弛下的变形进行了研究，主要结论如下：

（1）随应力松弛时间、循环峰值应力的增加，最大应变增加，而最小应变则随之减少；最大应变与最小应变均随循环次数的增加而增加.

（2）应力松弛时间增加，各循环中的加载应变降低，而残余应变增加；循环峰值应力增加，各循环的加载应变与残余应变均增加；各循环的加载应变与残余应变随循环次数增加而减少.

（3）黄麻织物/聚乙烯复合材料的相对残余变形指数，随应力松弛时间和循环峰值应力的增加而增加，随循环次数增加而减少.