长江口海域风浪场的计算与特征分析

耿浩博，张洪生，洪杨彬,，胡国栋

(1.上海海事大学 海洋科学与工程学院，上海 201306；2.浙江省嵊州市水利水电局，浙江 嵊州 312400；3.长江水利委员会长江口水文水资源勘测局，上海 200136)

长江口独有的三级分汊、四口入海的地貌特征，使其具有复杂的风浪特征。数值模拟是研究风浪场的常用方法，但以往在利用数值模拟方法研究长江口水域的风浪场时，要么只是数值模拟台风风浪场[1-4]，要么是对包含该区域的西北太平洋相关海域的风浪场进行整体的数值模拟和分析[5-8]。查阅公开发表的文献，未发现利用数值模拟通过计算连续多年的风浪场，进而统计分析长江口水域风浪特征的相关研究。

数值计算方法在20 世纪中叶被引入到海洋学研究。早期的海浪模型因没有考虑波浪内部的复杂性，因此模拟精度不高。随着波浪理论和计算机技术的发展，陆续提出了三代海浪数值模型[9]，其中WAVEWATCH III[10]（以下简称WW III）和SWAN[10-11]（Simulating Waves Nearshore）都属于第三代海浪模型。其特点是所有源项进行参数化之前，不对波谱加以限定，因此第三代海浪模型具有较强的适应性。

影响长江口海域波浪的因素复杂，除了当地的风场之外，外海传播过来的涌浪也是重要影响因素。为了提高风浪场模拟的精度，需要选择合适的计算范围。本文通过敏感性分析来分别确定WW III 模型和SWAN 模型的计算范围，其中确定SWAN 模型的计算范围时以WW III 模型的输出结果作为边界条件。

本文以ECMWF 数据资料作为输入风场，以ETOPO1 地形数据和实测水深资料相结合作为计算水深，通过将WW III 和SWAN 模型进行嵌套，计算长江口水域20 年（1996 年1 月至2015 年12 月）的风浪场；并选取1 个代表性站点，根据该站点已有的观测资料对计算结果加以修正；统计分析修正后的计算结果并利用风场数据资料，进而得出所选站点的风场和风浪场特征。

1 第三代海浪模型简介

WW III 是目前比较成熟的海浪数值模型之一，具有稳定性好、计算精度高等优点。SWAN 模型来源于WW III 等第三代海浪数值模型，采用隐式格式离散控制方程。与WW III 相比，SWAN 模型更适合地形多变的河口海岸水域风浪场的数值模拟，这是因为该模型能够有效地模拟波浪在浅水域传播变形过程中的特征，因此很多学者将两个模型进行嵌套计算[5,12-14]，其中文献[12]对两个模型进行嵌套计算的精度进行了详细论证。因此，使用这两种海浪模型进行嵌套计算是合理有效的。

在球坐标系下WW III 和SWAN 模型的控制方程均可表示为：

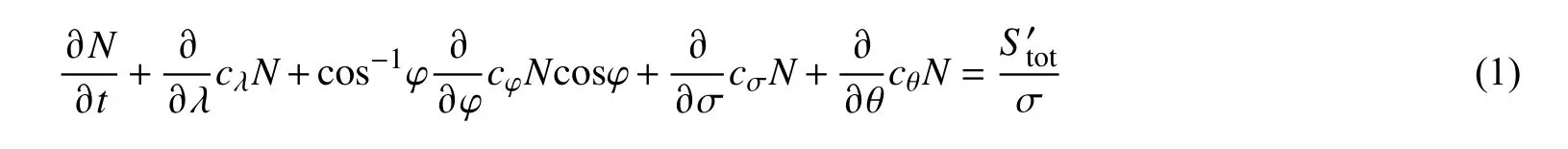
式中：t 为时间；σ 为相对频率；θ 为波向；λ 和φ 分别代表经度和纬度；cλ，cφ，cσ和cθ分别代表波作用量N 在λ，φ，σ 和θ 方向上的相应传播速度；为各物理过程中产生的源项，包括风能输入、波-波非线性相互作用和耗散项（白浪、水深变浅引起的破碎和底摩擦等），在WW III 和SWAN 模型中的形式略有不同，详见文献[10-11]。

2 模型建立与验证

风场数据的选择对风浪场模拟的精度有着重要影响。即使风场数据为实测数据，观测站点是否具有代表性也影响着最终结果的精度[12,15]。目前对海浪进行数值模拟时，主要使用ECMWF（European Centre for Medium-Range Weather Forecasts，欧洲中期天气预报中心）提供的风场。ECMWF 风场数据是当前高精度气象预报产品的代表[16]。文中采用分辨率为0.125°×0.125°的ECMWF 风场作为外强迫。

地形资料采用ETOPO1（1 Minute Gridded Global Relief Data Collection）海底地形数据和实测数据。ETOPO1 数据因其分辨率高达1′×1′，且包含冰面和基岩的情况，可以较好反映海底地形，所以是目前进行风浪场数值模拟时常用的地形数据[17]。考虑到长江口内水深地形复杂，因此在SWAN 模型的计算范围内，部分采用实测水深数据以体现长江口深水航道等水工结构物的影响，从而提高计算的精度。

长江口深水航道位于长江口南港北槽。北槽附近的牛皮礁（坐标为122°15′06″E，31°08′12″N，记为点P）具有较强的代表性（见图1），作为计算对象可以为今后航道整治和通航管理等提供参考。

图1 研究范围和代表性位置示意Fig.1 Sketch of study scope and representative location

在进行风浪场的数值模拟时，需要先确定模型的计算域和网格分辨率，因为这两者会严重影响计算精度和计算效率。如果计算域太小，就不能充分考虑在其他海域生成和传播而来的风浪，从而使计算结果产生较大的误差；如果计算域过大则又会增加不必要的计算时间。在确定计算网格分辨率时，同样需要遵循在满足计算精度的前提下，尽可能节省计算时间的原则。因为篇幅原因，文中只概述确定WW III 的计算范围和嵌套计算两个模型时网格类型的过程。确定SWAN 模型计算范围的方法与WW III 类似，故不再赘述。模型参数设定为手册的建议默认值。

2.1 计算范围的确定

首先基于往年的台风路径和寒潮影响范围，在长江口海域划定一个大范围区域（118°E～136°E，23°N～38°N）来确定WW III 的计算范围，再通过算例来讨论计算范围边界的具体位置。经过敏感性分析最终确定WW III 的计算范围为119°E～135°E，22°N～39°N；SWAN 的计算范围为121°E～124°E，30°N～33°N。图1（a）为计算范围示意图。

鉴于影响东边界和南边界所在区域海浪大小的主要因素为台风，文中以2013 年12 号台风“潭美”影响期间点P 的显著波高为计算指标，以1°为间距来确定东边界和南边界。而影响北边界和西边界所在区域海浪大小的主要因素为寒潮，所以以2010 年1 月发生寒潮期间点P 的显著波高为计算指标，以1°为间距来确定北边界和西边界。

在137°E 到132°E 之间、以1°为间距分别假定为东边界，并保持SWAN 的计算范围不变。WW III 的计算网格为6′×6′，SWAN 的计算网格为2′×2′。通过比较东边界不同经度时点P 的显著波高，以确定东边界的具体位置，计算结果如图2 所示。由图2 可见，东边界为138°E～133°E 时波高的计算结果基本重合，而取132°E 时波高发生了较明显变化。这说明在东边界取为132°E 时，计算区域外的风浪作用没有被充分考虑而导致计算结果不准确；而在东边界取为137°E～133°E 时，对于外海影响的考虑较为充分。为了慎重起见，在分析了5 年（2011—2015 年）影响中国东南沿海的西北太平洋台风运动轨迹后，取东边界为135°E。

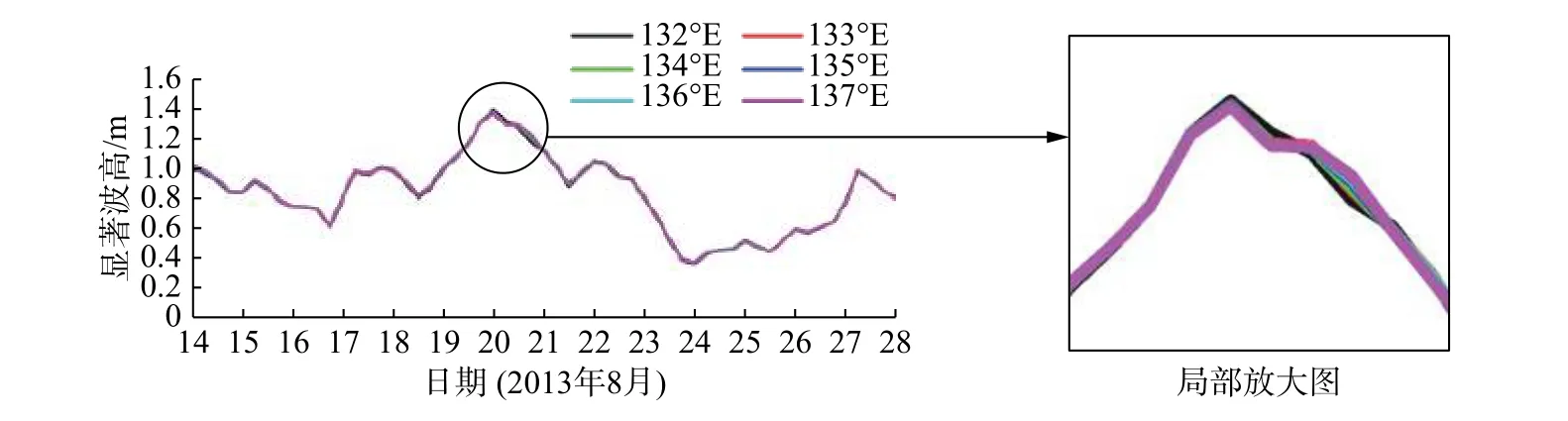
图2 东边界取不同经度时P 点的显著波高对比Fig.2 Comparisons of the calculated significant wave heights of point P with different east boundaries

用同样的方法确定其余边界，最终确定WW III 的计算范围为119°E～135°E，22°N～39°N；SWAN 的计算范围为121°E～124°E，30°N～33°N。

2.2 计算网格的确定

长江口滩槽相间的地形对海浪的传播有很大的影响，因此计算网格对计算精度会有很大的影响。WW III 的计算网格分辨率设置为6′×6′；SWAN 的计算网格分别设置为结构化网格（分辨率为2′×2′）和非结构化网格（分辨率略低于0.5′×0.5′）。以2014 年8 号台风“浣熊”作用期间点P 的显著波高为计算指标，将WW III 和SWAN 的嵌套计算网格对应组合，分别进行计算，并与观测资料加以对比（见图3）。用于对比的观测资料为牛皮礁水文站的现场观测数据。

图3 不同网格组合下P 点的显著波高对比Fig.3 Comparisons of significant wave heights of point P for different combinations of grid mesh

由图3 可见，采用非结构网格计算的显著波高与观测值较为接近，86.7%的差值在0.5 m 以内，采用结构网格计算的结果则与观测值有较大差距，最大差值达到了1.6 m 以上。因为计算的时间段内包括台风过程，所以该算例具有一定参考价值，可以较好地反映计算结果的精度。

基于以上分析，为了在保证精度的前提下提高计算效率，采用分辨率为6′×6′的WW III 模型网格和SWAN 模型非结构网格来嵌套计算长江口海域的风浪场。SWAN 模型计算范围内共有51 618 个三角形网格，26 103 个计算节点，与文献[18-20]所采用的网格分辨率近似。

2.3 计算结果的验证及修正

由于篇幅所限，图4 仅给出了2014 年7 月1 至28 日期间显著波高的观测值和计算值对比结果。由图4可见，计算结果较好地模拟了波高的变化趋势，两者吻合程度较好。图5 为2012 年到2015 年，共计4 年的显著波高的散点图。根据文献[12]中提出的验证方法对计算结果进行修正。综合4 年的结果来看，显著波高绝对误差为0.16 m，相对误差为18.63%，相关系数为0.82。依据算出的皮尔逊相关系数对两者进行线性相关分析，当相关系数为0.8～1.0 为极强相关。所以，显著波高的计算值与观测值两者为极强相关，在以往的研究中也得到了类似的结论[12]。因此，可以通过线性拟合对计算结果进行修正。

图5 显著波高的计算值和观测值散点Fig.5 Plot of the observed and calculated values of significant wave heights

根据散点图的拟合结果对显著波高做了如下修正：

式中：Hm为显著波高的修正值；Hc为显著波高的原始计算值。

修正后的显著波高见图4。由图4 可以看出，计算值修正后的结果要优于修正前。其中显著波高绝对误差为0.05 m，相对误差为8.24%。总体来看修正后波高的计算结果与观测值的吻合程度较为理想，计算结果可以有效地反映出台风过程所引起的波高变化。

图6 为波周期的观测值和计算值对比，图中波周期的计算值为平均波周期（TM01），为由波谱的零阶矩和一阶矩所求得的平均周期；波周期的观测值为谱峰所对应的周期。因为两者并没有直接对应关系，所以本文没有对周期进行修正。由图6 可以看到，两者的变化趋势一致，但是计算值明显小于观测值。其原因一方面与海浪模型本身有关，在以往的研究中也得到了波周期偏小的结论[12]；另一方面也符合在文献[21]中对两种不同类型波周期大小的分析，即通常谱峰周期会大于平均波周期。

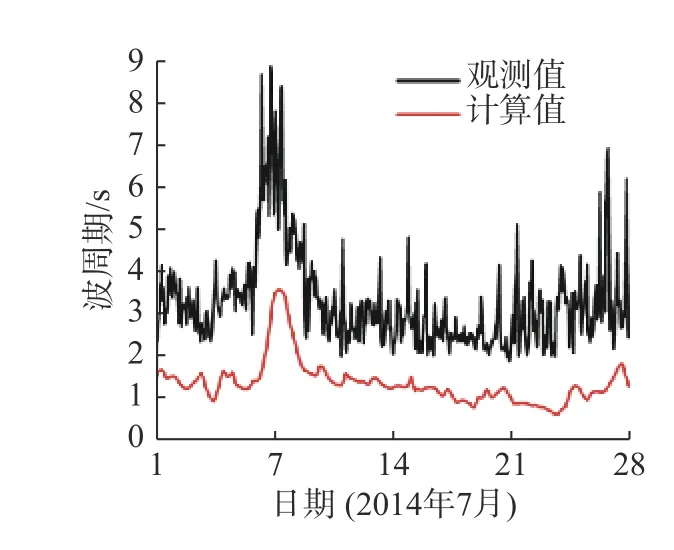
图6 波周期的观测值和计算值对比Fig.6 Comparisons of the observed and calculated values of wave periods

3 特征点的风浪特性统计与分析

3.1 风场特性统计与分析

利用ECMWF 风场数据，对点P 总计20 年的风场数据按16 个方向进行统计分析。表1 所示为点P 的多年各月平均风速；图7 为点P 的多年风玫瑰图。点P 多年平均风速为6.2 m/s。由表1 和图7 可见，全年常风向及大风向均为NW～NE，秋冬两季6 级以上大风的发生频率较高，且平均风速也大于春夏两季。

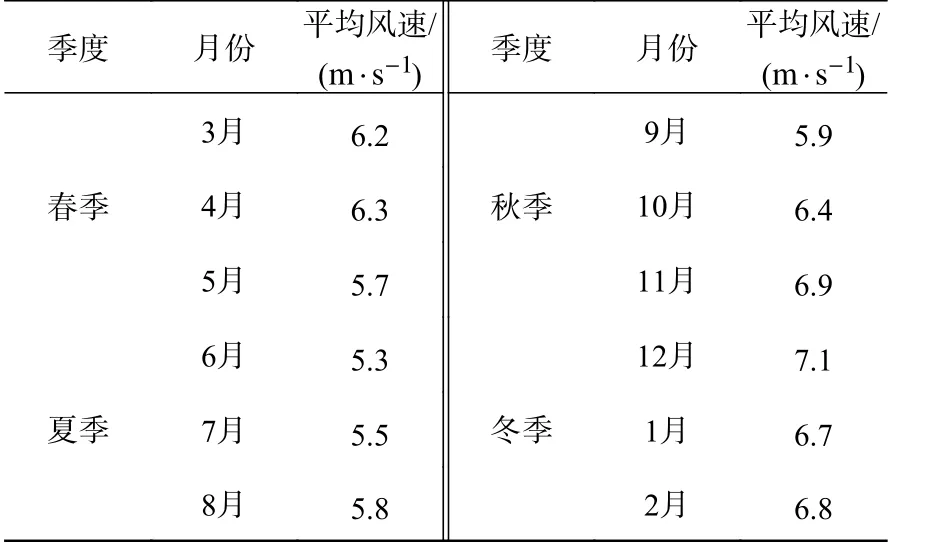
表1 点P 多年平均风速统计Tab.1 Average wind speeds for point P

图7 点P 多年风玫瑰图Fig.7 Wind rose plot of point P

由图7 可见，点P 常风向为N 向，WSW 向和W 向风频率最低。风向季节特征明显，冬季处于东北向季风时期，偏北风盛行，强风向多为NW～N；夏季受副热带高压影响，偏南风较多，风向以SE～S 为主；春秋两季为季风转换时期，春季风向以SE～S 向为主，N～NNE 向为次；秋季时冬季季风已开始增强，因此秋季风向以N～ENE 向为主。

3.2 波高和波向的联合分布

分别统计全年、各季度和各月修正后的点P 多年平均H1/10波高和波向特征。表2 为点P 的波高与波向联合分布表（全年）。由于篇幅原因，其他联合分布表未列出。图8 为点P 的多年各级波高玫瑰图。

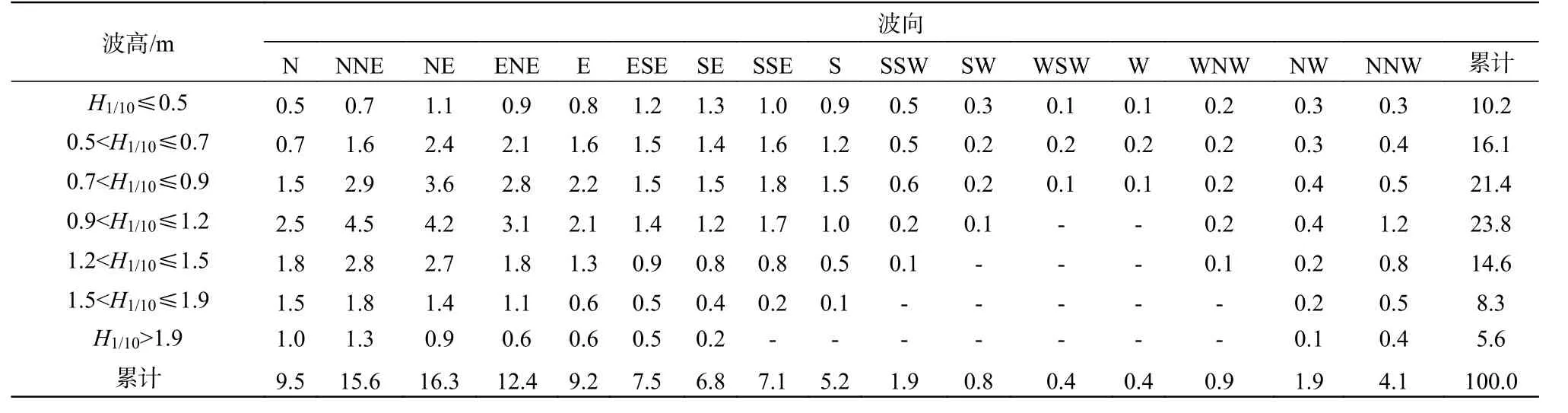
表2 点P 多年显著波高与波向联合分布(全年)Tab.2 Joint probability distribution of significant wave heights and directions for point P 单位：%

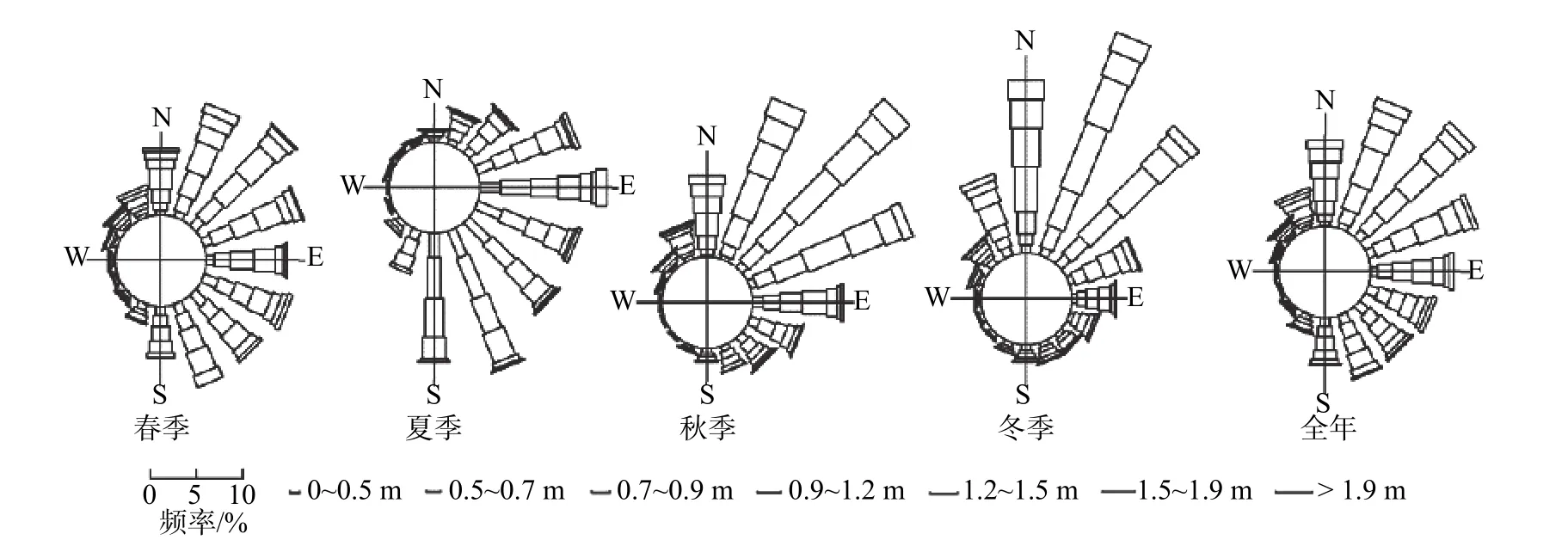
图8 点P 多年各级波高玫瑰图Fig.8 Wave rose plot of point P

由表2 和图8 可见点P 的H1/10波高主要分布在1.5 m 以下的波级，且集中分布于0.7～1.2 m，常浪向为NE 向，频率为16.3%。波高季节性变化明显，秋冬两季大浪出现的频率较高，这是由于秋冬两季处于冬季季风时期，此时的风速为全年最大。全年浪向主要分布于NE～S 连线的右侧。春季浪向以NNE～SSE 为主，夏季以ENE～S 为主，秋季以NNE～ENE 为主，冬季集中于NNW～NE。与文献[6-7]中所得到的波高与波向的季节特征相一致，主要原因均是受风场的影响。对比图7 和8 可见，浪向的季节特征与风向并不完全相同。例如，虽然夏冬两季都有相当比例的偏西风，但同向来浪频率却明显较低；虽然春季的偏东向风不多，但却有较多的同向风浪。这是因为风浪除了受风场影响外，外海涌浪和地形也是重要的影响因素。

3.3 波高和周期的联合分布

表3 点P 显著波高与波周期平均值的统计Tab.3 The table of averaged significant wave heights and mean wave periods for point P

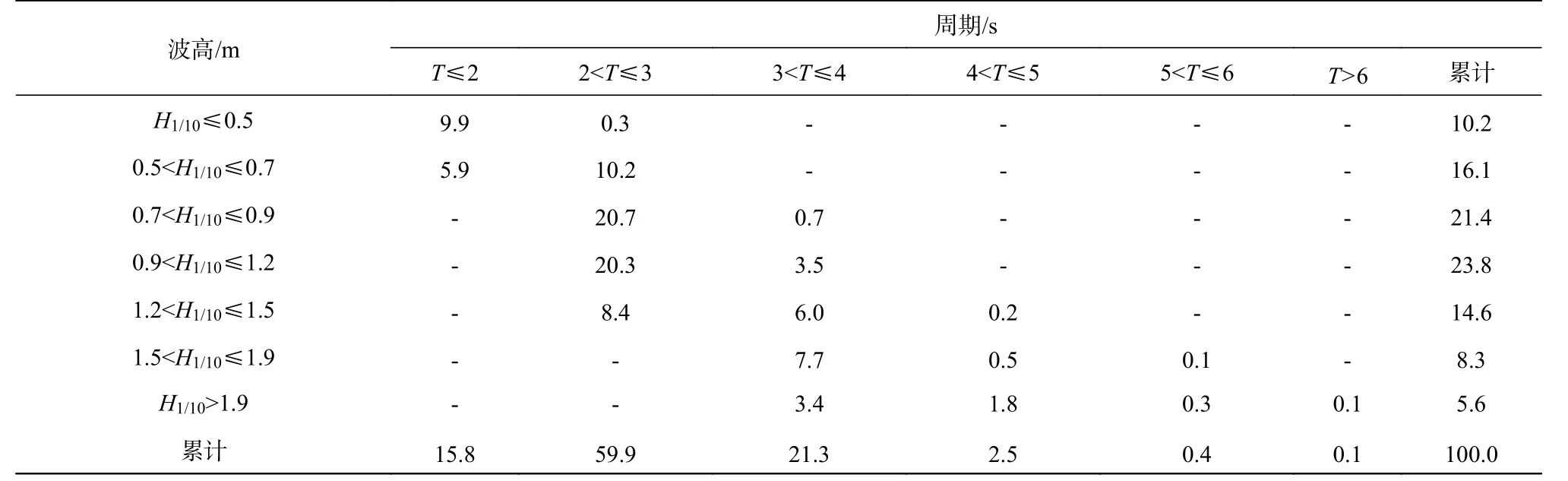
表4 点P 多年显著波高与平均波周期联合分布(全年)Tab.4 Joint probability distribution of significant wave heights and mean wave periods for point P 单位：%

3.4 不同重现期的风浪计算

根据计算的20 年的波高，假设点P 风浪极值满足耿贝尔极值I 型分布，分别计算了点P 不同重现期的H1/10极值波高，并对风浪极值进行了K-S 检验。检验结果表明，当置信度为0.95 时，接受点P 风浪极值满足耿贝尔极值I 型分布的假设。图9 为点P 不同重现期的H1/10极值波高图，其中点P 的50 年一遇极值波高为7.1 m。

因为极值波高的最大来浪向为E 向，所以计算了邻近海域E 向的极值波高分布，图10 为点P 邻近海域50 年一遇E 向极值波高分布图。从图10 可以看出，极值波高由东向西递减，这是由于东边是较开阔的外海，其水深和风速都较大，而无论是水深还是台风吹程都会影响波高的分布规律。

图9 点P 不同重现期的H1/10 极值波高Fig.9 Plot of extreme significant wave heights of point P for different return periods

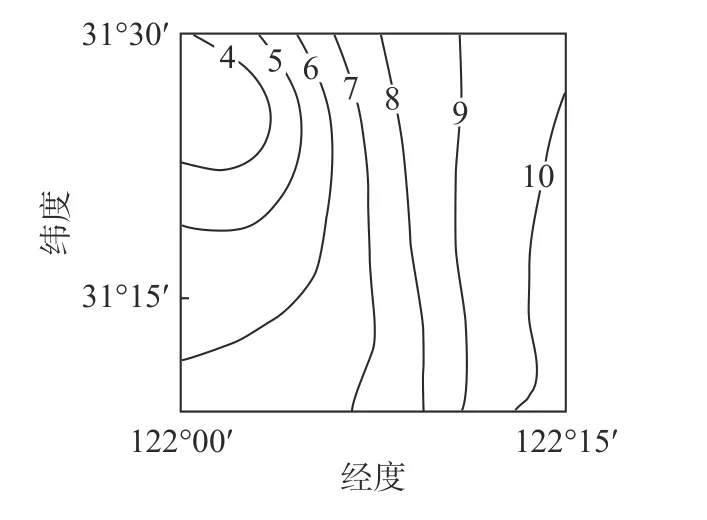
图10 点P 邻近海域50 年一遇E 向极值波高分布（单位：m）Fig.10 Extreme significant wave heights of 50 years return distribution (unit: m)

4 结 语

以ECMWF 数据资料作为输入风场，以ETOPO1地形数据和实测水深资料相结合作为计算水深，通过将WW III 和SWAN 模型进行嵌套，模拟计算了长江口海域20 年的风浪，并根据已有的观测数据对计算结果加以修正。根据风场数据资料和修正后的波高，统计分析了长江口水域具有代表性的点位—牛皮礁的风场和风浪场特性。

（1）牛皮礁处常风向为N 向，WSW～W 向来风最少。风向和风速随季节变化明显，冬季以北向季风为主；夏季以偏南风为主；春秋两季为季风转换时期，春季东南风稍多；秋季东北风稍多。秋冬两季受冬季季风影响风速大于春夏两季。

（2）受风场影响，牛皮礁处波高与波周期也有秋冬大，春夏小的特征。牛皮礁处常浪向为NE 向，出现频率为16.3%，W 和WSW 向浪出现的频率最小，为0.4%；季节特征明显，不过在地形和外海涌浪的影响下浪向与风向略有不同，浪向春季主要分布在NNE～SSE，夏季主要分布在ENE～S，秋季主要分布在NNE～ENE，冬季集中分布在NNW～NE。

（3）计算了牛皮礁处在不同重现期的H1/10极值波高和邻近海域50 年一遇E 向极值波高分布，结果显示50 年一遇的极值波高为7.1 m，附近海域极值波高呈现自西向东逐渐增大的特征。

本文的数值计算结果较好地体现了风场、地形和外海涌浪的作用，而且依据实测资料进行了修正。因此计算结果是合理的，统计分析和讨论所得出的结论是可信的。但实际的风浪生成和传播会受到多种因素的共同影响，因此风浪的数值模拟还可以进一步发展和完善。比如第三代海浪数值模型在周期的计算方面还存在一些不足，模型本身需要改进；此外，水位、潮流和风暴潮等都是影响风浪的重要因素，且长江口的地形因为工程建设原因在不断发生变化，在日后的研究中需要尽可能地将这些因素一并考虑，并采用分辨率更高的风场和地形资料，以得到更加符合实际的结果。