椭圆余弦波对V 形防波堤绕射波浪力的解析计算

2020-10-24才瀚涛

水利水运工程学报 2020年5期

才瀚涛，黄华，苏炜

(中山大学航空航天学院应用力学与工程系，广东广州 510275)

防波堤在近岸与离岸工程中用于抵抗波浪作用，从而对海工设施和海上作业水域实施保护。防波堤类型广泛，常见类型包括直立直墙式防波堤、岛式防波堤、梳式防波堤、斜坡式防波堤、T 形防波堤、潜堤、圆弧型防波堤以及V 形防波堤等。Stokes[1]推导了半无限长薄壁单突堤的波浪绕射解析解形式。Lick[2]解析探讨了楔形堤的微幅波绕射问题。洪广文[3]对不完全反射边界楔形堤和隅角堤的波浪绕射问题展开了理论分析。何军等[4]对T 型防波堤与波浪的相互作用进行了数值计算。胡宝琳等[5]对半圆型潜堤所受波压作用展开了数值模拟研究。朱梦华等[6-7]分别解析计算了椭圆余弦波对无限长直墙防波堤的波浪反射与透射作用以及波浪引起的防波堤底部的渗流作用。楚玉川等[8]对Airy 微幅波作用于单层圆弧型薄壁防波堤的绕射波浪力进行了解析研究。张敖等[9-10]分别应用椭圆余弦波和孤立波一阶模型推导并理论计算了浅水波对圆弧型防波堤的绕射力与波面。蒋学炼等[11]基于微幅波对单突堤的绕射解析理论，提出了单突堤总波浪力相位差修正公式，探讨了波浪力和波高的沿堤波动。V 形防波堤在美国首次提出并构建，其目的主要为建造可临时快速构建和撤收的结构系统。它具有建造方便省料和使用便捷且防浪效果良好等优点。Chang 等[12]数值研究了微幅波作用下的V 形防波堤的防浪效应。

本文基于椭圆余弦波的浅水波模型，推导任意张角下V 形防波堤的波浪绕射解析解，从而将现有的Airy 波模型和相应的各种结果加以有效拓展。此外，本文方法将对现有的无限长薄壁直墙堤对应的浅水波反射理论进行拓展。

1 椭圆余弦波对V 形防波堤绕射的波浪场解析解与波浪力算式

设在均匀水深为 d 的海域中设置有两臂长均为 a的 V 形固立防波堤（图1），取坐标系 oxyz(即坐标系orθz ）， oxy平面位于水底，原点位于堤的两臂相交点，ox正轴与下臂重合，两臂张角（即夹角）为 α，其中0<α ≤π， oz轴垂直向上。入射波为浅水波中的椭圆余弦波一阶分量，入射角（与 ox轴正向夹角）为β。以a为半径划一圆柱面，将流场划分为圆柱外流区 Ω0和圆柱内流区 Ω1与 Ω2（图1）。

设水波总速度 Φ=Φi+Φs=Re(φ)=Re(φi+φs)，其中Re 是对括号内取实部， φi为入射波势， φs为散射波势。则有：

图1 椭圆余弦波作用下的V 形固立防波堤Fig.1 Cnoidal wave diffracted by V shaped breakwater

另外， φ须满足V 形防波堤物面条件， φs须满足径向无穷远处的辐射条件。入射角为 β的一阶入射椭圆余弦波的波势[8]，可表达为：

其中，已利用贝塞尔母函数推广公式：

式中：kn=nk。由此若取对应流区 Ω(j)的椭圆余弦波总波势为则由特征函数展开法，可取：

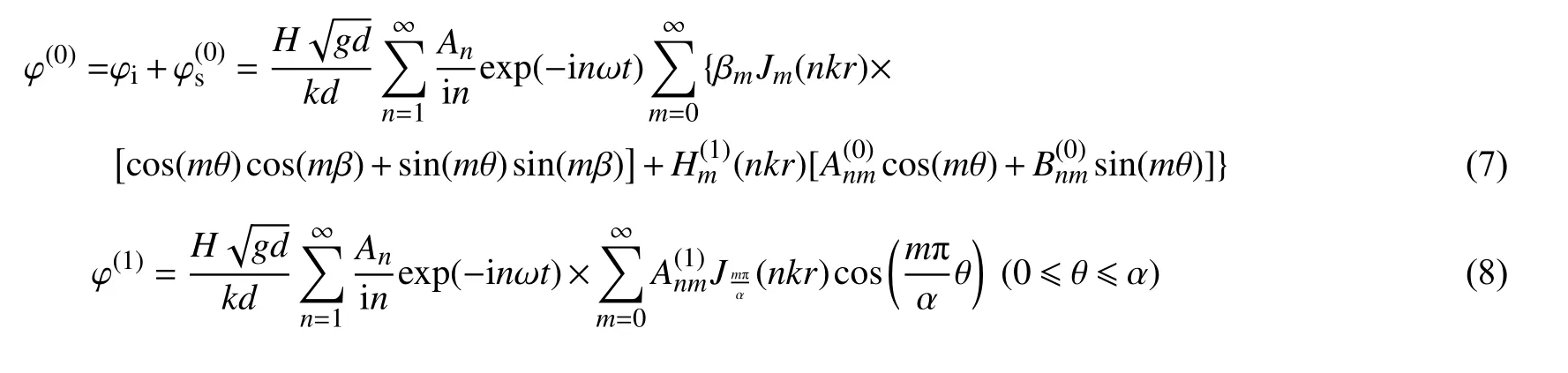
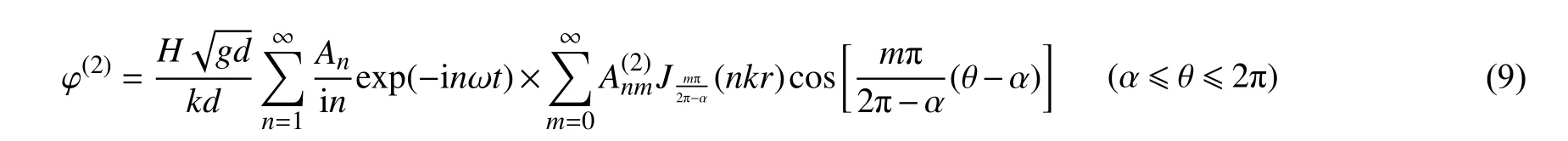
将各区圆柱交界面径向质点速度和压强连续条件统一写为：

由式(10)和(11)，可设并可得：

将 f(θ)在 0 ～2π上展开为傅氏级数，即：

由a0=al=bl=0 (l=1,2,3···)，相应有：

代入 f1(θ) 和 f2(θ)，分别可得系数方程为：

其中,

进一步应用边界条件式(12)和式(13)分别可得：

方程(20)，(21)，(26)和(27)构成了未知系数的无限维完备代数联立方程组，其中取实算中进行适度有限维运算即可满足计算精度要求。

对应流域 Ωj的绕射波面为而压力为(j=0,1,2)。

据此可得作用于防波堤上臂的总波浪力为：

相应分量分别为F1x=F1sinα，F1y=F1cosα，而防波堤下臂的波浪力分量为：

上臂和下臂的总波浪力为：

进一步可给出V 形堤总波浪力矩公式：

其中，下标 x和 y 分别对应绕 oy 轴和 ox轴的水平波浪力矩。

2 算例与分析

在以下计算的各图中规定符号 F/[ρg(H/2)ad]和 M/[ρg(H/2)ad2]分别表示V 形防波堤的无量纲总波浪力和力矩幅值。由于无量纲波浪力矩值为无量纲波浪力值的一半（见式(32)），故仅需对无量纲波浪力进行计算即可。在计算中引入椭圆余弦波特征参数λ =4κ2K(κ)/(3π2)=H/(k2d3)，它能够反映浅水波波浪参数与水深相对变化对波浪作用的综合影响效应。

在本文计算式中取V 形堤张角为π，进一步取有限长直墙薄壁密实防波堤堤长足够大，从而与文献[5]中涉及无限长直墙薄壁密实防波堤在水波正入射条件下的最大波面分布的相关计算进行验证比较。图2为与文献[5]所涉及的在相同参数条件下最大波面分布中心轴线剖面图的相关计算资料的比对结果，图中取符号η /H为无量纲化最大波面。图2 表明计算结果完全吻合，说明本文方法正确可靠。

图3 为不同臂长水深比下张角为2 π/3的 V 形堤在来波正入射下（β =π/3）最大无量纲波浪力随 kd的变化曲线。由图3 可见，当 0.53.0或kd<0.5时，最大无量纲波浪力随臂长水深比变化呈交错变化。

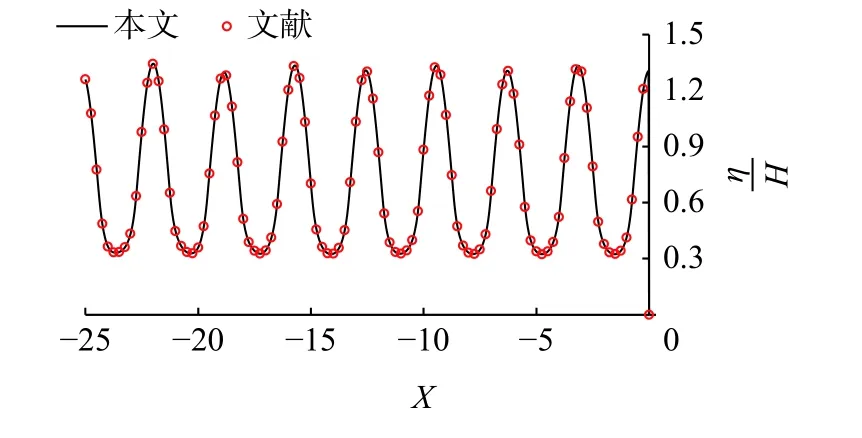
图2 与无限长密实直墙堤的中心线剖面的比较Fig.2 Comparation of central profile with infinite long solid wall (λ =1, a=1 000, d=2, α=π, β=π/2)

图3 不同臂长水深比下最大无量纲波浪力随k d的变化Fig.3 Maximum dimensionless wave force for different arm length-water depth ratio (β=π/3, λ=3, α=2π/3)

图4 为不同臂长水深比下张角为 π的V 形堤在来波正入射下（ βπ/2 ）最大无量纲波浪力随 kd的变化曲线。从图4 结果可知，当 kd 较小时（ kd<0.4），最大无量纲波浪力随着臂长水深比的增加而略有增加，之后小幅交错变换至 kd>2.0，对应值随着臂长水深比的增加而略有减小。与张角为 2π/3的V 形堤相比，张角为π的V 形堤的无量纲波浪力幅值受臂长水深比的影响明显要小许多。

图5 为不同来波入射角下张角为 2π/3的V 形堤的无量纲波浪力幅值随 kd的变化趋势。如图5 所示，当 kd<0.7时，无量纲波浪力幅值随入射角 β的增大而减小，当k d>0.7时，对应值呈现交错变化。

图6 为不同来波入射角下张角为 π的V 形堤的无量纲波浪力幅值随 kd的变化趋势。如图6 所示，随着入射角 β的增大最大无量纲波浪力随之减小。正入射（ β=π/2）对应的无量纲波浪力幅值最大，且kd>1.0时其值远大于斜入射情形的对应值。

图4 不同臂长水深比下最大无量纲波浪力随k d的变化Fig.4 Maximum dimensionless wave force for different arm length-water depth ratios (β=π/2, λ=3, α=π)

图5 不同来波入射角下最大无量纲波浪力随k d的变化Fig.5 Maximum dimensionless wave force for different incident angles (λ=3, d/a=1/5, α=2π/3)

图6 不同入射角下最大无量纲波浪力随k d的变化Fig.6 Maximum dimensionless wave force for different incident angles (λ=3, d/a=1/5, α=π)

图7 为不同张角下正入射波对同臂长V 形堤的无量纲波浪力幅值随 kd的变化趋势。图7 表明：不同张角下正入射波对同臂长V 形堤的无量纲波浪力幅值随张角的增大而明显增大，张角为 π的V 形堤对应最大无量纲波浪力幅值。

图8 为不同kd 下张角为 2π/3的 V 形堤最大无量纲波浪力随浅水波特征参数 λ的变化趋势。由图8 可知，当λ <2时，相对浅水条件（ kd=0.5）的无量纲波浪力幅值随 λ 增加而略增，随后随 λ略为单调减小。而对应 kd 的另外2 个取值，无量纲波浪力幅值均随 λ 增加而略减至保持不变。按照 λ=(H/d)/(kd)2，当 kd和V 形堤臂长a 不变条件下（由于 d=a/5，相应水深不变），则随λ 增大，波高H 增大。由最大无量纲波浪力表达式 F/[ρg(H/2)ad]，可见实际最大波浪力将随λ （即H）增大而明显增大。此外，图8 还表明，当 λ一定时，随kd的减小无量纲波浪力幅值增加。

图7 不同张角下V 形堤的最大无量纲波浪力随k d的变化Fig.7 Maximum dimensionless wave force for different opening angles of the breakwater (λ=3, d/a=1/5, β=π/4,π/3, π/2)

图8 不同 kd下最大无量纲波浪力随浅水波特征参数λ的变化Fig.8 Maximum dimensionless wave force for different characteristic parameters of shallow water (β=π/3, α=2π/3,d/a=1/5)

图9 为相同浅水条件下椭圆余弦波与Airy 微幅波对张角为 2π/3的V 型防波堤的最大无量纲波浪力的比较。由图9 可见，椭圆余弦波模型和Airy 波模型分别计算的防波堤最大无量纲波浪力随参数 kd的变化趋势大致相同。椭圆余弦波理论所算结果明显高于Airy 波理论的对应值，说明在一定浅水条件下采用椭圆余弦波模型十分必要。