拉索线形参数的解析解研究
2020-10-23旷新辉何雄君
旷新辉,江 海,殷 源,吴 超,何雄君
(1.湖北省路桥集团有限公司, 湖北 武汉 430056;2.湖北省联合发展投资集团有限公司,湖北 武汉 430000; 3.武汉理工大学 交通学院,湖北 武汉 430063;4.湖北省公路工程研究中心,湖北 武汉 430063)
0 引言
斜拉桥因跨越能力强、经济指标好以及结构形式新颖、美观等特点,已成为现代桥梁工程中最热门的桥型之一[1]。斜拉索作为斜拉桥结构中的主要承重构件,为梁体提供弹性支撑,将桥跨结构的自重以及桥面活载传递至索塔;同时斜拉索的存在使得梁跨截面的最大弯矩得以降低,提高了桥梁的跨越能力[2]。斜拉索是一种柔性结构,其在拉索自重和张力的作用下线形呈悬链线[3],实际斜拉索线形受端部张力、索长、弹性变形、几何非线性等因素的影响,拉索的线形问题一直以来都是桥梁工作者研究的热点[4]。
Bernoullis,Leibnitz,Routh,Feld先后计算得到了斜拉索的悬链线解,为斜拉索的静力分析奠定了基础,但其计算方法相当繁琐。Ernst在1965年提出了修正弹性模量的表达式——Ernst公式,考虑将曲线斜拉索用两节点直线杆来代替,通过修正斜拉索的弹性模量来考虑其刚度,但由于斜拉索位移和索力增量之间的非线性关系,这种算法会导致斜拉索索力和拉伸量之间关系的不闭合。张震陆等[5]提出了“悬链段”分析方法,对于一个特定的问题,只要求出各悬链段对应水平悬链的跨度及其他参数,即可得到待求量。该方法由于利用了水平悬链线的精确解,精度高于其他近似方法。彭力军等[6]提出了利用斜拉索索长来计算水平张拉力,以及通过斜拉索端部张拉力反求斜拉索索长的迭代方法。李强兴[7]推导了斜拉索的计算公式,假定水平张力为已知量来计算索长、倾角等,但从实际应用的角度考虑,其假定的索长和水平张拉力均是待求的未知参数,误差大。魏建东[8]推导了含待定参数的斜拉索线形的静力方程,可以应用于工程设计及强度验算,但该方法需要编程并进行迭代求解,在实际工程应用中不太方便。麦深林[9]利用斜拉索自重作用下斜拉索微段的静力平衡方程,推导出考虑弹性变形和不考虑弹性变形两种情况下斜拉索悬链线线形所对应的物理量,并提出了基于移动坐标原点的斜拉索简化计算方法。目前许多工程技术人员在计算中利用抛物线方程近似替代悬链线方程来求解斜拉索参数,该方法虽然能够满足一些工程应用的要求,但当处理有关斜拉索的非线性问题而又考虑弹性变形的影响时,就会遇到数学上的困难[10]。
因此有必要研究一种没有限制的精确计算方法,笔者在本研究中利用自重作用下任意微段的静力平衡方程,推导出斜拉索的线形理论公式,并从斜拉索的基本线形方程出发,推导出有工程应用价值的斜拉索参数。
1 拉索线形的解析解推导
如图1所示,以梁端锚点处为原点建立直角坐标系,塔端锚点坐标(X1,Y1),拉索上任一点坐标(x,y)。拉索在拉力N,重力场G的作用下,发生拉伸和下挠,任意微元体之间的拉力N、N~和重力ΔG满足力的平衡条件,以任意微元体的平衡条件构造拉索线形的微分方程并求解。

图1 斜拉索悬挂参数Fig.1 Suspension parameters of stay cable
根据斜拉索的微段平衡条件,计算图如图2所示。
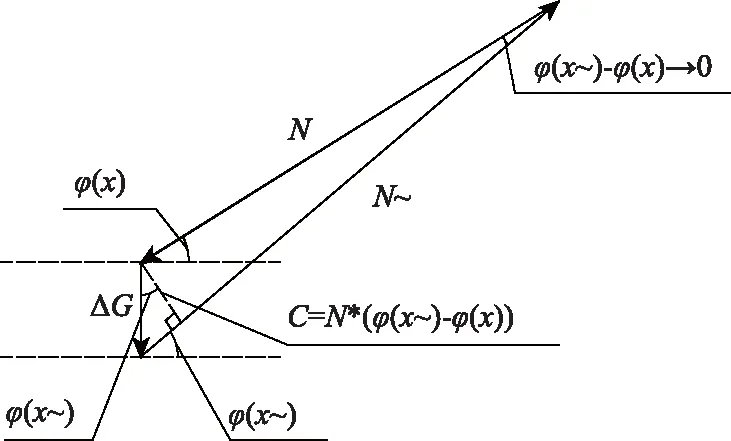
图2 斜拉索任意微段的平衡Fig.2 Equilibrium of any micro segment of stay cable
设拉索曲线方程为:
y=f(x),
(1)
则拉索任一点的水平夹角:
φ(x)=arctan[f′(x)],
(2)
(3)
(4)
任意微元体的重力:
(5)
式中,A为拉索正截面面积;N为拉索任意一点索力;E为拉索弹性模量。
微元体长:
(6)
索长:
(7)
由任意微元体的静力平衡可得:
(8)
C=N[φ(x+dx)-φ(x)]。
(9)
当dx→0时,C为正无穷小量。
将式(9)Taylor展开[11],取前2项,略去dx高次项,公式化简为:
C=Nφ′(x)dx。
(10)
将方程(3)~(6),(10)代入式(8),化简整理得:
(11)
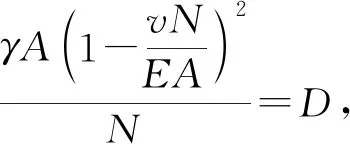
f″(x)-Df′(x)2-D=0,
(12)
(13)
参数D1,D2为解微分方程后的待定系数。将坐标系建立在梁端锚点,式中梁端锚点坐标为(0,0),塔端锚点坐标(X1,Y1),求出待定参数D1,D2。
D2=-1,
(14)
(15)
拉索的线形方程解即解析解为:
(16)
2 基于线形方程的拉索重要参数推导
根据推导的拉索线形方程,可以求解出:曲线索长ls、无应力索长l0、等效弹性模量Eeq、梁端锚点水平夹角φ(0)、塔端水平夹角φ(x)、拉索的垂度fm。
2.1 曲线索长求解
D可改写成为:
(17)
展开式(17),得:
(18)
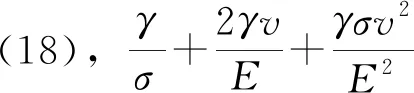
(19)
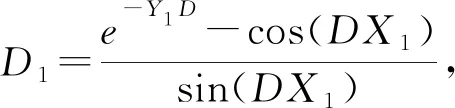
(20)
2.2 无应力索长求解
拉索在拉应力σ作用下发生体积变化,其体积变化满足体积柔量公式[12]:
(21)
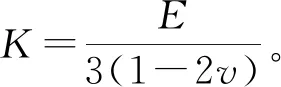
(22)
故:
(23)
2.3 拉索在任意应力下的等效弹性模量
(24)
将式(22)代入式(24)左侧,可求得任意应力σ作用下的Eeq。
(25)
(26)
展开式(26),后两项占Eeq的比值小于0.2%,做近似计算时,等效弹模公式[13-14]可简化为:
(27)
2.4 拉索梁端和塔端锚固角度求解
任意点拉索的角度为:
(28)
拉索梁端锚固角度:
φ(0)=arctan(D1)。
(29)
拉索塔端锚固角度:
(30)
2.5 拉索垂度求解
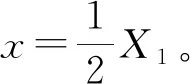
(31)
将f(x)表达式代入化简为:
(32)
2.6 拉索锚固点位移对索力的影响
拉索锚具变形、主塔与主梁弹性压缩、混凝土的收缩徐变对索力的影响本质上均由拉索锚点的几何变形导致。
考查式(24),拉索的锚点几何变形量可改写为:
(33)
求出:
σ2=EeqΔ+Δσ1+σ1,
(34)
应力变化值:
dσ=σ2-σ1=EeqΔ+Δσ1,
(35)
式中Δ为锚点间距变化增量[15](无量纲数):
(36)
3 算例
3.1 算例1
以文献[15]中提供的计算实例进行计算。取某长江公路大桥编号为J10,J18的斜拉索进行计算,计算方法分别采用Ernst公式[16-18]和本研究介绍方法。计算参数及计算结果如表1所示。
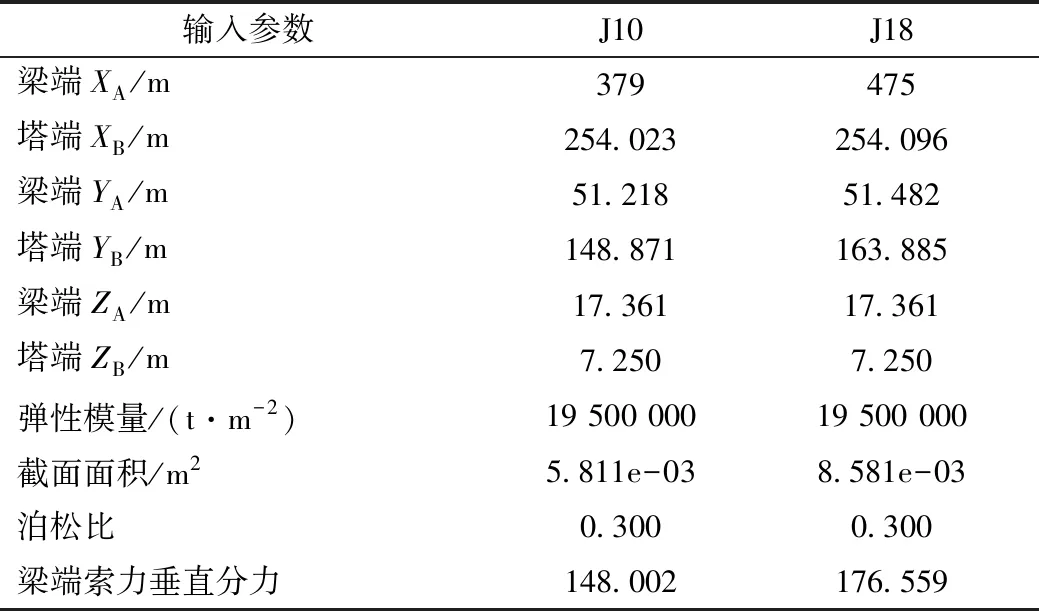
表1 某长江公路大桥斜拉索J10、J18计算参数对比Tab.1 Comparison of calculation parameter of stay cables J10 and J18 of a Yangtze River highway bridge
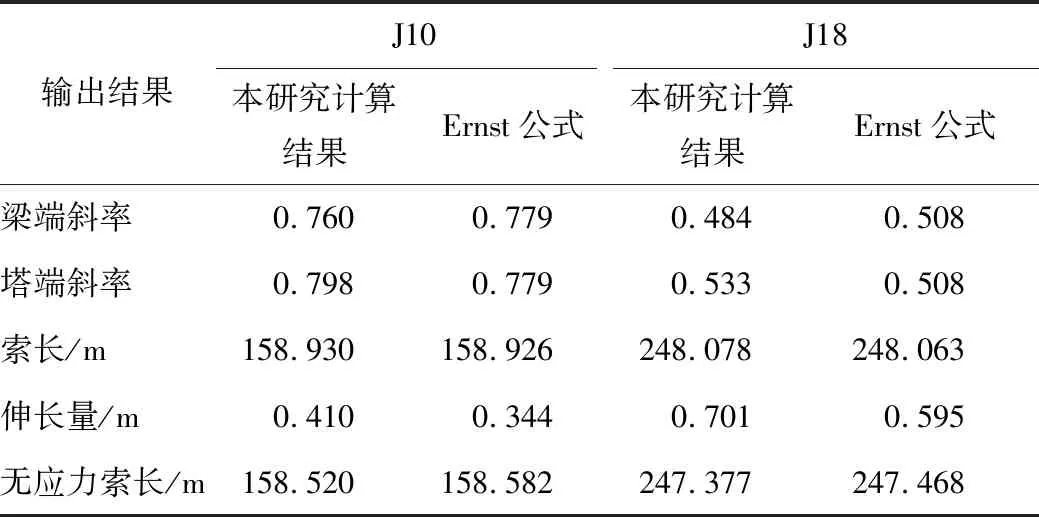
输出结果J10J18本研究计算结果Ernst公式本研究计算结果Ernst公式梁端斜率0.7600.7790.4840.508 塔端斜率0.798 0.7790.5330.508 索长/m158.930 158.926248.078 248.063 伸长量/m0.4100.344 0.7010.595 无应力索长/m158.520158.582247.377247.468
3.2 算例2
以笔者承担施工的某在建长江公路大桥为例,分别取M10,M20,M30,这3根索,按Ernst公式方法和本研究介绍方法进行计算斜拉索索长及无应力索长等参数,计算参数表及计算结果如表2所示。
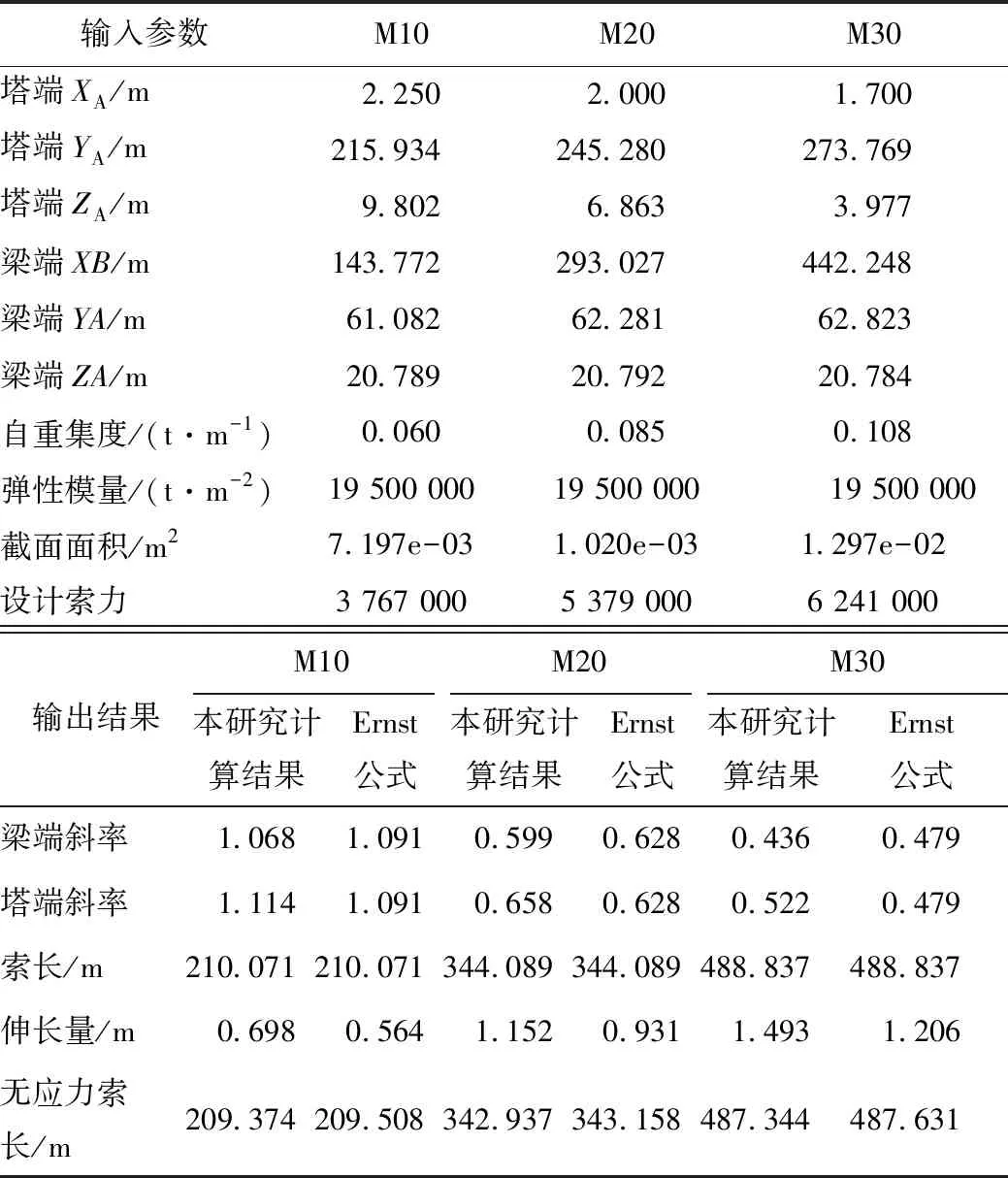
表2 某在建长江公路大桥斜拉索M10,M20,M30 计算参数对比Tab.2 Comparison of calculation parameters of stay cables M10, M20, M30 of a Yangtze River highway bridge under construction
实际施工M10,M20,M30,这3根索的无应力索长分别为209.379,342.940,487.351 m。这说明按Ernst公式计算的无应力索长偏长,而利用本研究计算方法的无应力索长等计算相对准确。
4 结论
本研究的拉索线形公式推导抛开了Ernst公式的假定条件,等效弹性模量推导直接利用广义胡克定律中的体积柔量公式,以上参数和结果均为理论推导值,避免了近似计算带来的误差,在超大跨度斜拉索的计算上有着更好的适应性,并在实际应用过程中得到验证。
