经济增速放缓与区域动态调节1

陈安平

0 引言

我国经济增长的速度近年来有所放缓，GDP年均增长率从之前的10%降至7%左右，且有下行压力。宏观经济的这一变化无疑会给区域经济带来冲击。(1)关于我国经济下行所带来的冲击，有研究认为是需求(比如出口下降)引起，但更多研究认为是由于供给因素(比如人口红利消失)造成(见Cai, 2016; Chen and Groenewold, 2019; Lin, 2019; Tian, 2019)。本文是从总体上考虑经济增速变化所带来的冲击，并未具体区分是哪一类型的冲击。由于我国区域之间存在明显的空间差异，各地对宏观冲击的响应可能不同。比如，在2012年，除新疆和甘肃外，其他省份的地区生产总值增长率都有所下降，其中天津、山西、内蒙古和辽宁的降幅最为明显，较上一年下降约3个百分点，而北京、上海、宁夏和云南的变化相对较小。到2017年，天津、山西、内蒙古和辽宁的增长速度进一步下滑，与2011年相比下降超过6个百分点，除了这几个省份外，吉林、湖北、四川、重庆、甘肃、青海等地的增速也有较大幅度下降，但另一些省份如北京、上海、浙江和广东则变动很小。显然，宏观经济增速减缓时各地的表现差异明显，且有动态变化的趋势。(2)如果用2012年后其他年份的数据来做比较，也能得出同样的结论。

现有文献主要是从全国总体层面分析我国经济增速放缓的原因、效应及应对策略(比如，刘伟和苏剑, 2014; 刘树成, 2015; 蔡昉, 2016a; 林建浩和王美今, 2016; 郑挺国和黄佳祥，2016; 王少平和杨洋, 2017; 陈彦斌等, 2018; Lin et al., 2016; Bai and Zhang, 2017; Lu, 2017; Blagrave and Vesperoni, 2018; Lin, 2019; Tian, 2019)，很少有文献从区域层面展开研究。(3)一个例外是姚树洁(2015)，他从区域层面分析了经济增速放缓背景下经济发展的路径，认为发达地区要冲在技术和资源利用的前沿，大力推进产业升级换代，欠发达地区要通过交通、信息等手段，加快承接沿海地区传统产业的转移。本文拟弥补这个不足。具体而言，本文将关注以下问题：宏观经济增速减缓这一冲击对区域经济带来了什么影响？这些影响是否具有空间异质性？各区域面对宏观冲击时是如何自我调节的？对于这些问题的研究不仅具有重要的政策含义，也有助于深化对我国经济增速放缓的理解。

为了回答以上问题，本文提出了一个分解方法，把区域产出增长率分解为就业、资本、劳均产出和单位资本产出四个部分，然后利用2000年后的省级数据建立差分模型，通过比较受冲击影响较大区域和较小区域就业、资本、劳均产出和单位资本产出增长率等在冲击前后的变化，来识别宏观经济冲击对各地的影响及机制。其中的一个难点在于如何测度经济增速放缓给各地带来的冲击。如果简单地以各省地区生产总值增长率的变化来衡量冲击，则可能存在较大误差，因为各地的经济增长除了受宏观冲击的影响外，还受区域特定因素的影响。为了克服这个问题，本文采用Bartik(1991)的偏离份额(shift-share)方法，结合全国各个产业增加值的增长率和冲击前各省相应产业所占比重，构造了一个测度宏观经济冲击的指标。

本文研究发现，宏观经济增速放缓对各地的影响显著不同，从区域自我调节来看，资本的响应要快于就业，但持续的时间相对较短。与受冲击影响较小区域相比，受冲击影响较大区域的就业和资本，特别是二、三产业的资本增长率明显偏低，表明这些区域受到冲击后劳动力和资本发生了外流。但从资本产出率和人均产出两个指标来看，受冲击影响较大区域的增长率要高于其他区域。这似乎是一个悖论，一方面这些区域的劳动力和资本在流出，另一方面其生产率在提高。本文给出了一个解释，即经济增速放缓时企业面临的竞争压力加大，但投资于创新的机会成本降低，因此受冲击影响较大区域更愿意投资于高技术产业，从而推动产业结构升级，有助于提升其生产率。利用各省高技术制造业和高技术服务业的投资数据，本文给出了支持该解释的证据。

通过从区域视角展开研究，本文突破了现有文献仅从全国总体层面分析经济增速放缓的局限，为我国经济增速的变化研究提供了一个新的方向。实际上，国际上已有许多研究讨论总体经济变化对区域经济的影响。比如，Hoynes et al. (2012)和Yagan (2019)研究了美国经济衰退对各州就业和失业的影响，Bitler and Hoynes (2015)比较了经济波动时美国各州贫困率的变化。也有研究分析经济波动对微观个体的影响，比如Guvenen et al. (2014)使用美国个人收入微观数据，分析了前1%高收入人群的收入和其他人群相比，在经济衰退前后有何不同，Jensen and Johannesen (2017)研究了金融危机对丹麦个人消费信贷的影响。然而，针对我国经济增速放缓的研究，目前尚停留在从全国层面分析其原因、效应及应对策略上。

本文拓展了宏观冲击区域效应文献的研究内容。此类研究多从就业和工资等出发，讨论各种冲击对区域经济的影响。比如，Dix-Carneiro and Kovak (2017)分析了贸易自由化对巴西各区域就业和工资的影响，Hershbein and Kahn (2018)研究了经济衰退对美国各地不同技术工人需求的作用，Feyrer et al. (2017)讨论了技术冲击对美国各州就业与工资的影响。本文把区域产出分解为资本、就业、劳均产出和资本产出率，通过比较各分解变量在经济冲击下的响应，对区域自我调节机制有了更深入的理解。本文研究显示，资本的调节速度要快于人口和就业，这说明研究宏观冲击的区域效应时，至少在关注短期效应时，资本和资本产出率是不可或缺的指标。

熊彼特的破坏性创新理论表明，经济状况不好时，创新的机会成本降低，企业更愿意投资于创新产品，低生产率的企业会被淘汰，让位于高生产率的企业，本文的发现在一定程度上支持该理论。本文研究也与竞争压力理论(Hall, 2005; Gibbons and Roberts, 2012)相符，即经济增速放缓时，企业之间的竞争加剧，破产倒闭的风险增高，此时企业会更注重效率而非增长。有文献提供了相应的经验证据，比如，Hershbein and Kahn(2018)的研究显示，经济下行时企业更倾向于提高对高技能劳动力的需求。与之不同的是，本文是从投资，而不是人力资本角度出发，发现受冲击影响较大区域更倾向于投资高技术产业，推动产品升级换代，从而提高这些区域的生产率。

本文也丰富了产业结构升级的研究文献。研究表明：相对于第三产业，第二产业对宏观冲击的响应更强，高技术制造业的发展对于产业结构升级的作用突出。刘伟和蔡志洲(2018)通过比较中美两国的三次产业结构，认为我国已完成了由传统结构向现代结构的转化，但与发达国家相比，在结构升级，特别是第三产业的发展上还有很大空间。韩永辉等(2017)以及袁航和朱承亮(2018)等从产业政策和国家高新区等视角分析了三次产业结构升级的影响因素。与这些研究相比，本文不仅关注三次产业，还从高技术制造业和高技术服务业视角分析了产业升级，发现高技术产业，特别是高技术制造业是推动产业结构转型升级的关键，这与孙早和许薛璐(2018)的发现相一致。

论文其余部分的安排如下：第1部分提出了把产出进行分解的方法，并对区域产出四个分解变量的变化做了描述性分析。第2部分给出了计量模型，构建了衡量冲击的指标，对变量的设定及数据来源做了说明。第3部分是实证结果，从资本、就业、单位资本产出、劳均产出和人均产出等几个方面分析了宏观冲击对区域经济的影响，也报告了稳健性检验结果。第4部分进一步分析了经济增速放缓时各地投资于高技术产业的不同表现及其影响。最后是论文的结论。

1 区域产出分解

宏观经济冲击下区域层面可观测到的一个明显特征是产出增长率的波动，而这又缘于资本和劳动力空间配置的调整及其生产率的变化。鉴于此，本文从区域产出增长率入手，将其分解为四个部分，即就业增长率、资本增长率、劳均产出增长率和单位资本产出增长率，通过各分解部分在经济增速放缓前后的变化来识别宏观冲击对区域经济的影响，分解方法具体如下。

假设区域产出为C-D生产函数：

Y=AKαLβ

(1)

其中Y表示产出，K表示资本，L表示劳动力或就业，A,α和β为参数，对式(1)两侧取对数再取微分，则可得到下式：

dlnY=αdlnK+βdlnL

(2)

式中d表示微分，ln表示取对数，式(2)可转化为：

(α+β)dlnY=αdlnK+βdlnL+(α+β)dlnY-αdlnK-βdlnL

(3)

经过整理，上式可写为：

(α+β)dlnY=αdlnK+βdlnL+α(dlnY-dlnK)+β(dlnY-dlnL)

(4)

两侧同除以α+β，令a=α/(α+β),b=β/(α+β)，则有

dlnY=adlnK+bdlnL+adln(Y/K)+bdln(Y/L)

(5)

由于对数的微分近似于增长率，这样，通过上式可把产出增长率分解为就业(L)、资本(K)、单位劳动的产出或劳均产出(Y/L)、单位资本的产出或资本产出率(Y/K)的增长率，其中前两项表示生产要素的调整，后两项分别表示劳动生产率和资本生产率的变动。实际上，式(5)是一个恒等式。尽管本文从C-D生产函数出发推导出该分解式，但式(5)本身并不需要以C-D生产函数为条件，只要满足a+b=1这个条件，该分解式即成立。

式(5)可以用来分解区域产出，但这并不表明区域产出和各分解部分之间存在任何因果关系，不能简单地以各分解部分对区域产出增长率的回归来识别经济增速放缓的影响。在接下来的实证研究中，本文将构造一个能捕捉宏观经济变化时各地所受影响的外生冲击变量，然后把式(5)中的四个分解部分在全国经济增速放缓前后的变化作为因变量，分别对该冲击变量进行回归，据此探究宏观冲击对各地生产要素及其生产率的影响。

图1展示了2001至2016年间全国31个省、直辖市和自治区产出增长率四个分解变量的平均值。(4)产出、资本与就业的变量定义和数据来源见论文第2节的说明，受资本数据所限，本文没有分析2016年后的变化。可以看出，各变量的变化趋势不同。相比于其他分解变量，资本增长率是最高的，除个别年份外，都在10%以上。从趋势来看，2001到2010年间资本增长率逐年递增，但从2011年起，增速开始下降，到2016年降至10.8%，比2010回落3.8个百分点。就业增长率的趋势和资本类似，但波动更为明显。在2011年前就业增长率保持上升态势，2011年达到12.6%，但此后开始下降，到2016年，就业增长率仅为3.9%。单位资本产出增长率是四个分解变量中最低的，在多数年份中甚至为负，但从趋势看，2014年后有比较明显的上升态势。劳均产出的增长率相对较高，在2010年达到7.5%后，开始下降，但从2013年起，又有回升趋势。总之，图1表明，尽管区域产出增长率四个分解部分的差异明显，波动的时点和幅度并不完全一致，但一个共同特征是，近年来其增长趋势有明显变化。

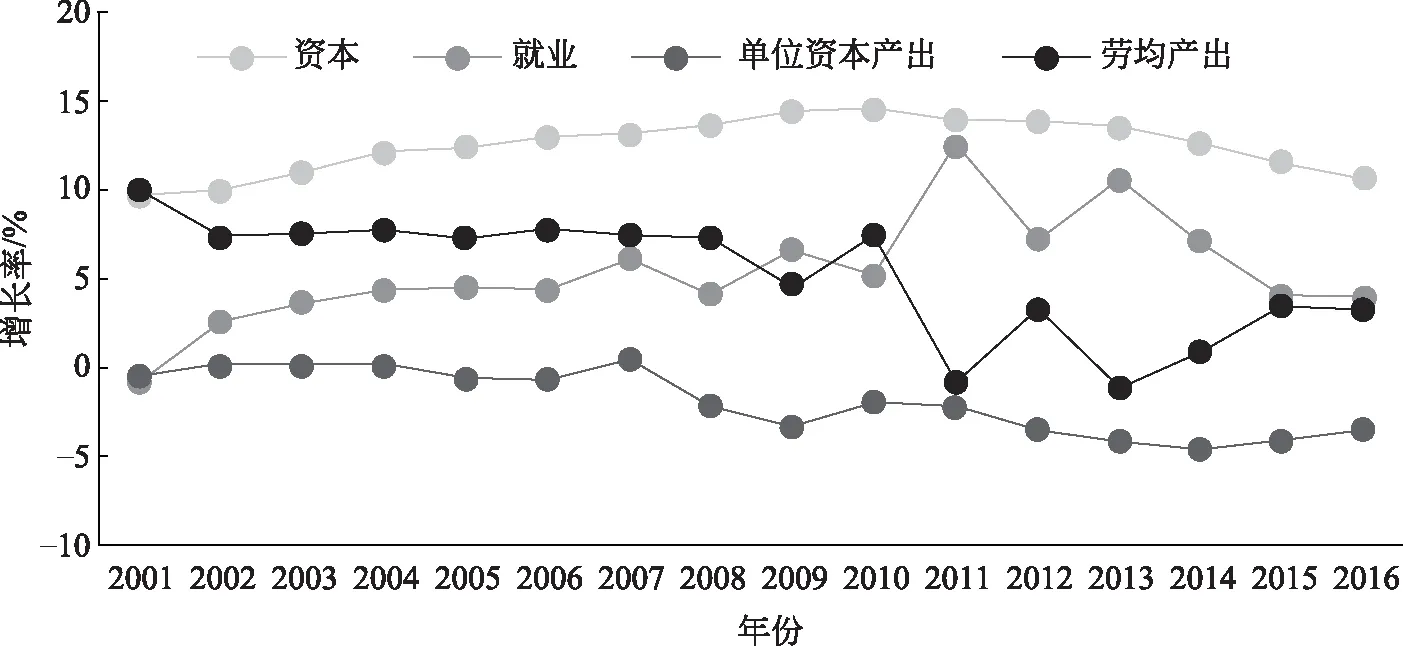
图1 资本、就业、单位资本产出和劳均产出增长率

以上分析是基于全国所有省份的平均值，如果从各省之间的比较来看，其差异更为明显。为了观察宏观经济冲击前后各省资本、就业、单位资本产出和劳均产出增长率的变化，根据全国GDP增长速度的变化，把样本时期分为三个部分，即2001—2006年，2007—2012年和2013—2016年，其中第一个时期对应经济高速增长时期，第二个时期为经济减速时期，第三个时期为中高速增长时期。(5)三个时期划分的详细说明见论文第2节。然后计算各省产出增长率四个分解变量在第一和第三个时期的平均值，再用第三个时期的均值减去第一个时期的均值，结果报告在图2中。

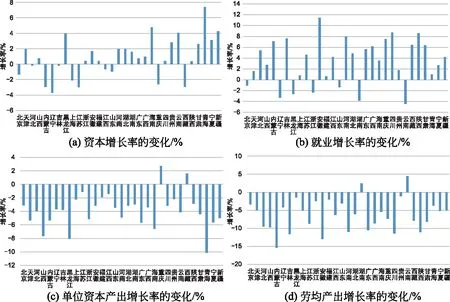
图2 省际之间资本、就业、单位资本产出和劳均产出增长率

从图2(a)可看出，资本增长率的变化在省际之间的差异非常明显，有11个省份的资本增长率在2012年后有所下降，其中内蒙古、辽宁、上海、江苏和重庆降幅最大，超过了3个百分点。其他省份的资本增长率在2012年后有所上升，其中内陆省份如内蒙古、云南、青海和新疆等地的表现最为抢眼，青海的资本增长率在2012年后甚至提高了7.4个百分点。

就业增长率的变化如图2(b)所示，多数省份的就业增长率在2012年后有所提高，其中安徽、河南、四川和陕西等中西部省份的就业增长率增加了约8个百分点，内蒙古、吉林、重庆、西藏和甘肃的增幅也超过了6个百分点。在就业增长率下降的省份中，辽宁、黑龙江、湖南和云南等地比较突出，其降幅在3个百分点左右。

单位资本产出增长率的变化如图2(c)所示，与投资和就业增长率的变化明显不同，除了个别省份如重庆和西藏外，其他地区单位资本产出的增长率在经济增速放缓后有所下降，其中，山西、黑龙江、海南和青海下降最为明显，降幅超过了6个百分点。图2(d)表明，劳均产出增长率的变化和单位资本产出增长率类似，除了湖南和云南两省之外，2012年后其他省份在下降，其中有7个省份的降幅甚至超过了10个百分点，内蒙古更是超过了15个百分点。

总之，以上分析表明，区域产出增长率四个分解变量的趋势在近年来有所变化。分省来看，多数省份的资本和就业增长率在全国经济增速放缓后有所提高，单位资本产出和劳均产出的增长率在2012后则有所下降。无论是哪一个指标，省际之间的差异都非常明显，这在一定程度上表明各地受宏观经济冲击的影响可能不同。以下将建立计量模型，将各分解变量的变化与各地受到的冲击联系起来，据此研究宏观冲击的区域效应。

2 计量模型、变量和数据说明

本文以省(自治区、直辖市)为单位，采用2000至2016年的数据，通过不同省份受冲击影响程度的差异，来识别宏观冲击对区域产出各分解变量的影响。具体做法是以各省就业、资本、劳均产出、单位资本产出的增长率在冲击前和冲击后的变化为因变量，对冲击变量和年份固定效应的交乘项进行回归，计量模型设定如下：

Growi,t-Growi,2007=α+βPreGrowi,2000—2006+(gshocki×It)γI+It+Reg+εit

(6)

其中Grow是就业、资本、劳均产出、单位资本产出的增长率，i和t分别表示省份和年份，PreGrow是冲击前这些变量的增长趋势，gshock是衡量经济增速放缓所带来的冲击变量，I是年份固定效应，Reg是区分东中西三大区域的虚拟变量，ε是随机误差项。

模型的左侧是冲击后各省就业、资本、劳均产出、单位资本产出增长率与冲击前这些变量增长率的差值。本文从2013年开始分析宏观冲击的影响，即t=2013,2014,2015,2016，冲击前的年份选为2007。因此模型的因变量是2013年及其后各年就业、资本、劳均产出、单位资本产出增长率与这些变量在2007年的增长率之差。这样选择年份的主要考虑是我国GDP的增长率在2007年达到了一个峰值14.2%，此后有所回落，自2012开始一直在8%以下，从高速增长转为中高速增长。(6)以2012年为我国经济增速变化的一个时间节点是文献中的通行做法，比如蔡昉(2016b)的研究。因此将样本时期分为三个阶段，其中2000—2006年为冲击前，2013—2016年为冲击后，2007—2012年则用来测度冲击。

考虑到冲击前增长快的区域受冲击的影响可能会大于增长慢的区域，因此在模型中包含了各变量从2000到2006年的增长率，以控制冲击前各省的增长趋势(PreGrowi,2000—2006)对估计结果的影响。(7)之所以没有用更早的时期来衡量冲击前的趋势，是考虑到2000年前的经济可能受其他冲击，比如1997年金融危机的影响。对于冲击变量(gshocki)，本文采用各省2012年和2007年产出增长率预测值之差来衡量，下文将做详细说明。通过在模型中引入冲击变量和年份固定效应的交乘项(gshocki×It)，可以估计冲击对各省经济在2013年及其后各年的影响。γI是本文关注的关键系数，其含义在于：与受冲击较小区域相比，受冲击较大区域的就业、资本、劳均产出、资本产出等变量的增长率(相对于冲击前)在冲击后是上升了，还是下降了。比如，当t=2013时，γI的估计系数衡量的是各变量2013年的增长率与2007年相比，受冲击的影响有多大。当t=2014,2015,2016时，其含义依次类推。式(6)实际上是差分模型，控制了省级层面不随时间变化的因素。为了消除经济波动对结果的可能影响，在模型中加入年份固定效应。考虑到三大区域之间存在明显的异质性，在模型中加入了表示东中西部的虚拟变量。(8)东中西三大地区的划分采用传统方法，东部包含北京、天津、河北、辽宁、上海、江苏、浙江、山东、福建、广东、海南和广西，中部包含山西、内蒙古、吉林、黑龙江、安徽、江西、河南、湖北、湖南，其他省份为西部。为了减轻误差项可能存在的相关性，将采用聚类稳健标准误(clustered error)。(9)我们也尝试了稳健标准误(robust error)，发现冲击效应的显著性在多数情况下有所增强。

式(6)中gshocki表示各省受到的宏观冲击大小，这是本文的关键变量。文献中衡量宏观冲击的常用变量是失业率(比如Bitler and Hoynes, 2015)，但由于缺少每个省历年来的调查失业率数据，此方法对本文研究并不可行。一个类似的方法是用各省产出的实际增长率来衡量。但区域经济增长除了受宏观冲击的影响外，还受区域特定因素的影响，如果用各省产出的实际增长率作为衡量冲击的指标，则可能不能准确度量各地受到的冲击。为了克服这个不足，本文采用两步法，先用全国各产业增加值的增长率和每个省的产业结构来预测各省的增长率，再用冲击前后预测值的差值来衡量各地受到的冲击。其中第一步，采用文献中常用的Bartik(1991)偏离份额(shift-share)方法，假设全国第S个产业增加值的增长率为gNS，i省第S个产业所占的比重为ShareiS，那么i省经济增长率的预测值为：

(7)

本文根据上式，用2007年和2012年全国各产业增加值的增长率，结合2004到2006年间各省各产业增加值所占比重的平均值即其产业结构，来预测各省在2007年和2012年的增长率。第二步再用两者之差来度量各地所受到的冲击大小(gshocki)。之所以用2007年前的产业结构数据，而不是2007—2012年的数据，是为了避免2007年后经济增长对产业结构的影响，使用3年的平均值是为了减轻经济波动对结果的影响。对于产业划分，采用了9大产业的分法，包括农林牧渔业、工业、建筑业、批发零售业、交通运输业、住宿餐饮业、金融业、房地产业、其他行业，具体划分及数据来源见国家统计局网站上的“国家数据”。(10)本文也尝试基于19个行业分类的就业数据来构造冲击变量，但结果并不理想，一个可能的原因是国家统计局公布的分行业就业数据仅包含“城镇单位就业”，涵盖的就业范围有限，不能准确衡量各产业就业变化。采用偏离份额法构造冲击变量是文献中的常用做法(Blanchard and Katz, 1992; Notowidigdo, 2011; Hershbein and Kahn, 2018; Acemoglu and Restrepo, 2020)。由于各省的产业与全国对应产业受到的冲击相似，而且在预测各省产出增长率时采用的是冲击前的产业结构，因此用该方法为各省构造的冲击变量与各地在经济增速放缓时期的特定因素无关，体现的只是各地受宏观冲击的影响，是一个比较理想的外生冲击变量。

为了对gshock变量有一个直观的印象，图3展示了2012年和2007年各省经济增长率预测值的差值。显然，与2007年相比，所有省份2012年的增长率都有一个较大幅度的下降，说明各省都受到了负的冲击。其中增长率下降最为突出的是北京和上海，其降幅约8个百分点，天津、浙江、江苏和广东也下降了7个百分点左右，西藏和海南下降的幅度最小，不到5个百分点。从分布来看，处于10%分位的省份(新疆)的增长率预测值下降了5.3个百分点，而处于90%分位的省份(天津)的增长率预测值下降了7.1个百分点，两者之间相差约2个百分点。(11)如果用各省产出的实际增长率来做比较，处于10%分位和90%分位省份的增长率相差约7个百分点。这在一定程度上反映产出实际增长率比预测增长率包含更多“噪音”，说明实际增长率除了受宏观冲击的影响外，还可能受各省特定因素的影响。总之，各省之间经济增长率的变化存在明显的空间差异，即使在东中西三大地区内部，这种差异也比较明显。本文正是利用这种空间差异来识别经济增速放缓对各省资本、就业、资本产出率、劳均产出的影响。由于gshock的数据为负值，为了便于解释，在下文的实证中，对gshock做了符号反向处理，即数值越大表示该省所受冲击越大。

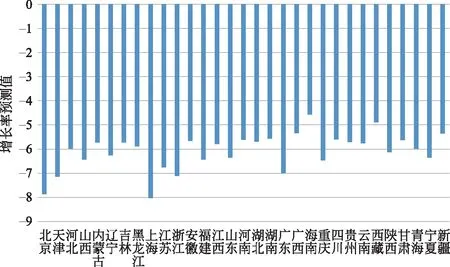
图3 gshock的空间分布

为了观察以上计算的冲击变量gshock和产出实际增长率之间的关系，根据模型(6)，以2001年到2016年各省产出增长率和2007年产出增长率的差为因变量，对gshock和时间固定效应的交互项进行回归，系数估计结果见图4。(12)为了观察整个样本期间产出增长率和冲击变量gshock的关系，回归从2001年开始，因此没有加入冲击前的趋势变量，也没有加入地区虚拟变量。其中系数估计值的大小用图中的黑点表示，其90%置信区间用长虚线表示。从图中可以看出，在2005年前，系数估计值为正，表明在此时期受冲击影响较大区域的产出增长率(相对于2007年)要高于受冲击较小区域。在2005年至2006年两年间，经济增长率在各省之间几乎没有差别。从2007年起，受冲击影响较大区域实际产出增长率的降幅明显大于受冲击影响较小区域，这种趋势一直延续到2011年。从2012年起，情况发生了改变，受冲击影响较大区域的情况有所改善，其与受冲击影响较小区域经济增长率的差距不断缩小。以上比较显示，本文构造的gshock变量和冲击测度时期(2007—2012)产出实际增长率的变化联系紧密，但与冲击前和冲击后经济增长率的变化关联度不高，这说明gshock是度量经济增速放缓冲击的一个较好指标。

图4 区域经济增长率和冲击变量的关系

模型(6)中其他变量如就业、资本、劳均产出、单位资本产出等的具体设定如下：对于就业，本文采用各省城镇单位就业来衡量，即城镇国有单位就业、集体单位就业、其他单位就业、私营企业个体就业的加总，数据来源于《中国劳动统计年鉴》和《中国人口和就业统计年鉴》各期。(13)早期的统计年鉴公布各省总的就业，但近年来出版的年鉴仅公布城镇单位就业，为了保持数据的一致性，本文采用了城镇单位就业。资本是根据盘存永续法推算而来，具体见Wu(2016)。(14)各省2000—2016年的资本数据由Wu(2016)论文作者，澳大利亚西澳大学经济系吴延瑞教授提供。各省的产出及其增长率数据来源于《中国统计年鉴》各期，和资本一样，采用以2010年为基期的实际值。劳均产出是各省产出与就业的比值，单位资本产出或资本产出率为各省产出与资本存量的比值。

3 实证分析

3.1 就业所受影响

根据模型(6)，本文首先估计宏观经济冲击对就业的影响，结果见表1。从第(1)列的估计结果可看出，冲击效应(即冲击变量与时间固定效应交乘项)的系数在4年中都为正，但无论哪一年，系数均不显著。这说明从总体上看，经济增速放缓对各省就业的影响并无显著差异。考虑到面对冲击时，各种类型经济体的自我调节模式可能不同，因此把就业分为国有单位就业、集体单位就业、私营企业和个体就业以及其他单位就业，再利用式(6)分别进行回归，结果报告在表1的第(2)到第(5)列中。(15)本文所用就业数据为“城镇单位就业”，与各产业很难精确对应，因此这里按所有制类型分类，而没有按产业来分类研究，在下文研究资本所受影响时，采用了三次产业的分类。从这些估计结果来看，对于国有单位和其他单位就业，冲击效应的系数多数为负，但仅在2013年其他单位就业的估计结果中显著。对于集体单位就业，冲击效应的系数在前两年为正，后两年为负，但只在2014年显著。对于私营个体单位就业，冲击效应的系数在4年中均为正但显著性不高。总之，分经济类型来看，宏观冲击的影响在区域间有所不同，但冲击效应显著的较少，这和总体就业的估计结果类似，说明即使分不同经济类型来看，经济增速放缓对就业的影响也不明显。

表1 就业效应的估计结果

对于控制变量，冲击前的增长趋势在集体单位就业的回归中显著为负，在其他回归中系数为正但不显著，说明除集体单位外，2007年前的增长趋势对各省就业增长率之间的差异没有显著影响。年份固定效应多数为负，在其他单位就业的回归中显著，说明就业增长率近年来有下降趋势，东部和中部虚拟变量系数的显著性不高，表明就业增长率的变化在三大地区之间没有显著差异。(16)以2013年作为基准年份，因此没有将其包含在模型的年份固定效应中。类似地，西部地区作为基准组，也没有包含在模型中。从模型拟合度来看，其他单位就业回归模型的拟合度最高，调整后的R2值超过了0.5，私营和个体单位就业的拟合度最低，R2值仅为0.1。

以上所用就业数据是城镇“单位就业”，并未包含所有就业，回归结果或许不能准确反映经济增速放缓后各地的就业变化，因此采用各省常住人口作为就业的一个替代变量，再用模型(6)进行估计。(17)比如在2016年，全国总的就业是7.7亿人，其中城镇就业为4.1亿人，城镇单位就业为3.9亿人。采用这种做法主要是考虑到一个区域的人口和就业高度相关，人口的变化能在一定程度上反映就业变化。由表1第(6)列的估计结果可以看出，采用人口数据后，结果明显不同。从冲击变量和时间固定效应的交互项来看，4个年份的冲击效应都为负，且从2014年起高度显著。这说明宏观冲击对各省人口的影响明显不同，与受冲击影响较小省份相比，受冲击影响较大省份的人口增长率下降更多(或增加更少)。(18)式(6)中的冲击效应实际上是双重差分(difference in difference)的估计结果，即与2007年的增长率相比，2013年后各省增长率的变化值之间的比较。冲击效应系数为负，表明受冲击影响较大区域的增长率相较于2007年下降的幅度大于(或增加的幅度小于)受冲击影响较小区域。从系数估计值(绝对值)的大小来看，冲击效应从2014年的0.39上升到2015年的0.68，增加了74%。到2016年，系数有所回调，但仍超过0.6。为了对冲击效应的大小有一个直观的理解，以2016年为例，其系数估计值表明，从2007年到2016年，与受冲击影响较小(比如处于10%分位)省份相比，受冲击影响较大(比如处于90%分位)省份的人口增长率多下降(或少增加)约1.1个百分点。(19)90%和10%分位省份所受冲击大小之差为1.8个百分点，所以人口增长率的变化之差为0.018×0.633，约1.1个百分点。对此，一个可能的解释是，经济增速放缓时人口从受冲击影响较大省份流向受冲击影响较小的省份。有意思的是，人口的这种调整从2014年才开始变得显著，这说明受到宏观冲击后，区域人口的调整有一定的时滞，但持续的时间较长。另外一个发现是，采用人口变量后，冲击前的增长趋势、年份固定效应和地区虚拟变量都变得显著，其中冲击前的趋势变量系数为负，说明2007年前人口增长快的区域在宏观冲击后的增长率会相对降低。从模型的拟合度看，采用人口变量后也有明显提高。

为什么宏观经济冲击下人口在各地的变化如此突出，而就业却不明显？一个可能的解释是由于户籍制度，常住人口的变化更多体现的是外来人口，或者说是外来农村人口的变化，这一部分人群技能水平相对较低，受宏观经济变化的影响较大。其原因在于经济增速下滑时，抵御市场波动风险能力相对较弱的中小企业，特别是生产效率较低的企业，容易受到影响、易于关门倒闭。而这类企业是吸纳外来农村劳动力的主力，其经营状况的变化会直接影响到对外来农村劳动力的就业需求，进而影响其流向。由于本文所用的就业数据并未完全涵盖这一部分人群，所以从估计结果来看，采用城镇单位就业时，就业效应不显著，但采用常住人口作为代理变量后，冲击效应显著为负，且持续较长时期。

3.2 资本所受影响

资本受宏观冲击影响的估计结果见表2。从该表第(1)列可看出，与2007年相比，从2013年到2016年间受冲击影响大的省份相对于受冲击影响小的省份资本增长率下降更多(或增加更少)，但区域间的这种差异并不显著，而且系数的绝对值随着年份的增加在减小。从控制变量来看，冲击前增长趋势变量的系数为负且显著，表明冲击前资本增长率越高的区域受经济冲击的负面影响越大。东部和中部地区虚拟变量的系数为负且显著，说明东部和中部地区资本增长率显著低于西部。时间固定效应的系数均显著为负，表明资本增长率有逐年下降的趋势。模型的拟合度较好，其R2值约为0.5。

表2 资本效应的估计结果

考虑到不同产业面对宏观冲击时的响应可能不同，从总体上研究各省资本增长率受冲击的影响会掩盖产业之间的差异。因此按照三次产业的划分，逐个估计宏观冲击对三次产业资本增长率的影响，结果报告在表2第(2)到第(4)列中。从这些估计结果可以看出，对于第一产业而言，冲击效应的系数在2013年和2014年为正，此后两年为负，但仅于2013年在10%水平上显著。这说明经济增速放缓对第一产业资本增长率的影响在区域之间没有显著差异，尽管年份固定效应的估计结果表明第一产业的资本增长速度有逐年递增的趋势。

第二产业的结果则明显不同，4年中冲击效应的系数都为负，2013年和2014年系数的绝对值甚至超过了2，且高度显著。这表明与受冲击影响小的省份(比如处于10%分位的省份)相比，受冲击影响大的省份(比如处于90%分位的省份)第二产业的资本增长率(相较于2007年)要低4.3～4.5个百分点。(20)以2013年的估计结果为例，由于90%和10%分位省份所受冲击大小之差为1.8个百分点，所以资本增长率的变化之差为0.018×2.488=0.045，即4.5个百分点。为了便于说明，以天津(处于90%分位)和新疆(处于10%分位)为例，从实际数据来看，2007年两地第二产业的资本增长率分别为11.3%和9.1%，到2013年，两地第二产业的资本增长率分别为14.6%和16.3%，天津的增长率提高了3.2个百分点，而新疆提高了7.2个百分点，前者比后者低4个百分点，这略低于从模型估计结果得出的推断。(21)采用资本增长率的实际数据，是为了比较资本增长率的变化，该变化和模型中冲击效应系数的估计值并不等同，后者衡量的是宏观经济冲击对区域间资本增长率变化的平均影响。从2015年和2016年系数的估计值来看，其绝对值有所减小，且变得不再显著。

对于第三产业，表2第(4)列的估计结果表明，冲击效应的估计值在4个年份中都为负，且高度显著。与第二产业相比，第三产业系数的绝对值相对较低。比如在2013年，第三产业冲击效应的系数为-1.7，仅为第二产业系数的68%，这说明宏观经济冲击对第三产业资本增长的影响小于第二产业。第三产业的另一个明显特征是，冲击效应在2014年回调后逐年上升，到2016年冲击效应的绝对值甚至超过了2013年。这表明宏观冲击对第三产业的资本增长有持续累加的影响，不同区域之间第三产业资本增长率的差异会不断拉大。

总之，以上估计结果表明：从总体上看，经济增速放缓对资本增长率的影响在区域间并无显著差异。分三次产业后，经济冲击对第一产业的作用仍不明显，但对第二产业有显著的负面影响，其冲击效应在2013年最大，此后逐年下降，从2015年起变得不再显著。对于第三产业，冲击效应在4年中都为负且显著，其系数的绝对值在前两年小于第二产业，但有一个逐年增强的趋势。如果比较资本和人口冲击效应的系数大小，可以发现宏观冲击对资本的影响要大于人口，且更为迅速。这说明面对经济增速下滑，资本的调节速度快于人口，可能是由于相对于资本，人口在区域间的转移需要更多时间的缘故。

3.3 劳均产出和单位资本产出所受影响

宏观冲击对劳均产出影响的估计结果见表3第(1)列，为了节省篇幅，表中仅报告每年的冲击效应。从中可以看出，从2013年到2016年，劳均产出所受的冲击效应为负，其系数在前三年显著。这说明经济增速放缓对劳均产出有一定负面影响。但如前文所述，本文所用的就业数据为城镇单位就业，存在一定局限，由此计算的劳均产出可能不能准确度量各地劳动生产率的变化，因此用人口作为替代变量，计算人均产出，再估计经济冲击对人均产出的影响。从表3第(2)列的估计结果可以看出，与劳均产出结果明显不同，冲击效应的系数现在符号为正，其大小和显著性呈逐年递增的态势。2013年系数估计值为0.032，到2016年其系数增至0.795，且在5%水平显著。这说明与受冲击影响小的省份相比，受冲击影响大的省份人均产出的增长率相较于2007年提高更多。

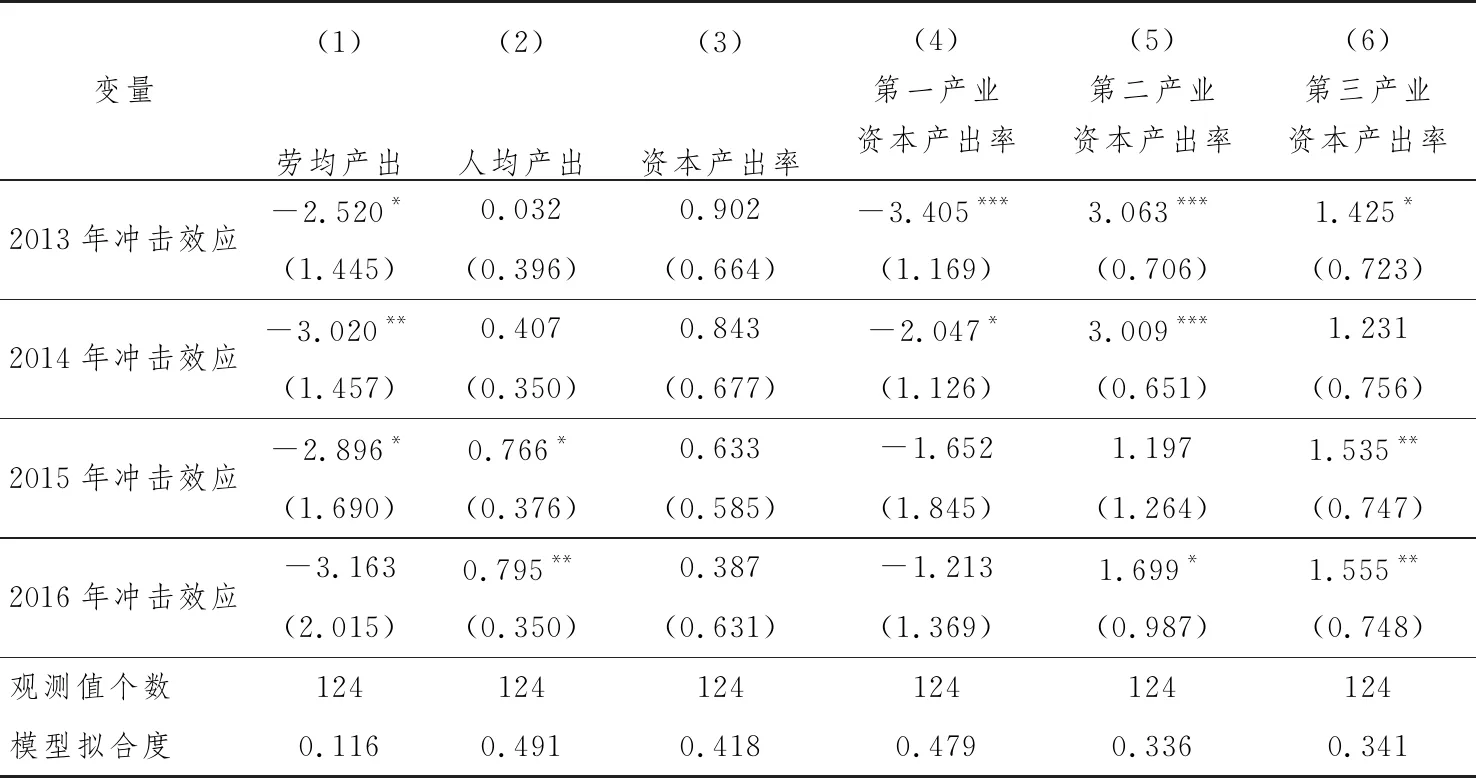
表3 劳均产出和单位资本产出效应的估计结果

表3的第(3)到第(6)列报告了单位资本产出的冲击效应估计结果。从第(3)列可看出，单位资本产出增长率对冲击的响应在4年中都为正，但系数均不显著，说明从总体上看，宏观冲击对资本产出率没有显著影响。从三次产业的划分来看，结果有所不同。对于第一产业，冲击效应为负，且在前两年显著，说明冲击对第一产业资本产出率有负面影响；对于第二产业，冲击效应为正，2013年和2014年在1%水平显著。这说明相较于受冲击影响较小区域，受冲击影响较大区域第二产业的资本产出率在2013年后增长更快。从系数大小来看，第二产业资本产出率的冲击效应有逐年减小的趋势，但到2016年，56%的冲击效应依然存在，且在10%水平显著；对于第三产业，4年中冲击效应的系数都为正，系数的大小和显著性在2014年后不断增强，这表明经济增速放缓对第三产业资本产出率有显著影响。

前文研究表明，受冲击影响较大区域资本和人口的增长率相对较低，假如生产要素的边际生产力递减，那么以上所发现的经济冲击对人均产出和单位资本产出的影响会不会是由于这些区域资本和人口流向其他区域所引起，而并非冲击本身的作用？为了对此加以判断，在模型中加入资本增长率和人口增长率在冲击前和冲击后的差，重新估计模型，发现人均产出冲击效应的显著性有所下降，但单位资本产出，特别是第二产业单位资本产出的冲击效应几乎没有变化。(22)为了节省篇幅，估计结果未列出。这说明，即使资本和人口外流在一定程度上有助于受冲击影响较大区域人均产出和单位资本产出增长率的提高，但冲击效应依然存在，还有其他因素影响资本和劳动的生产率，论文第4部分将对此做进一步的研究。

3.4 稳健性检验

为了检验以上结论的稳健性，本文尝试了4个实验。首先，考虑到北京、上海和天津等地的产业结构和其他省区相比明显不同，将其包含在样本中可能会引起偏差，因此在样本中剔除这些地区；此外，也尝试从样本中剔除海南和西藏等受冲击影响较小的区域；其次，以上回归是用2007年作为基准年份来做比较，但并非所有省份在2007年都达到经济增长的高点，因此采用其他年份比如2006年为基准年份来做比较；(23)比如对于河北和山东，增长率2007年的低于2006年。最后，使用其他年份来衡量冲击前的增长趋势，比如，使用2001—2006年、2002—2006年，以及2003—2006年的增长率，以观察不同时期的增长趋势对结果的可能影响。检验结果表明，在这些实验中，本文的基本结论，即宏观经济增速放缓时，与受冲击影响较小区域相比，受冲击影响较大区域的资本和人口增长率相对下降，但单位资本产出和人均产出的增长率却相对提高，是稳健的。(24)为了节省篇幅，估计结果未列出。

4 进一步的讨论

为何与受冲击影响较小的区域相比，受冲击影响较大区域的资本和人口增长率相对较低，但其人均产出和资本产出率，特别是二、三产业的单位资本产出增长率相对更高？本文认为：熊彼特的破坏性创新理论可以提供一种解释，即经济下行时，受冲击影响较大区域投资于创新品的机会成本相对较低，所以创新更容易出现，低生产率的企业会被市场淘汰，让位于高生产率的企业，从而使区域生产率升高。此外，竞争压力理论(Hall, 2005; Gibbons and Roberts, 2012)也可以用来解释本文的发现，即宏观经济状况不好时，企业面临的竞争压力增大，为避免被挤出市场，企业不得不进行创新或升级产品，从而有助于提高区域生产率。无论哪种理论，都强调创新或新产业的发展是经济增速放缓时生产率得以提升的一个主要途径。考虑到高技术产业是创新最为活跃的部门，本文在式(6)中加入高技术产业投资与冲击效应的交乘项，据此对以上解释加以验证，具体如下：

(8)

其中tech为各地高技术产业投资占比。如果以上的推断正确，那么可以预期λI的符号为正。考虑到制造业和服务业之间在高技术产业上的差异明显，本文区分高技术制造业和高技术服务业，其界定参考了国家统计局发布的《高技术产业(服务业)分类2018》和《高技术产业(制造业)分类2017》。具体而言，结合《中国固定资产投资统计年鉴》中行业大类的划分，将医药制造业、铁路、船舶、航空航天和其他运输设备制造业、计算机、通信和其他电子设备制造业以及仪器仪表制造业等划归为高技术制造业，将信息传输业、软件和信息技术服务业、科学研究和技术服务业等划分为高技术服务业。(25)《高技术产业分类》中的行业精确到了4位码，而《中国固定资产投资统计年鉴》是按行业大类来划分的，按这两个标准来匹配高技术产业会有一定偏差，但在尝试逐步增减高技术产业所涵盖的行业大类后，结果并无明显变化。在此基础上，首先把《中国固定资产投资统计年鉴》中各省高技术产业对应的行业投资数据加总，然后分别计算高技术制造业占制造业投资的比重，以及高技术服务业占服务业投资的比重。(26)由于没有找到《中国固定资产投资统计年鉴2014》，2013年的数据来自《2013固定资产投资统计年报》。

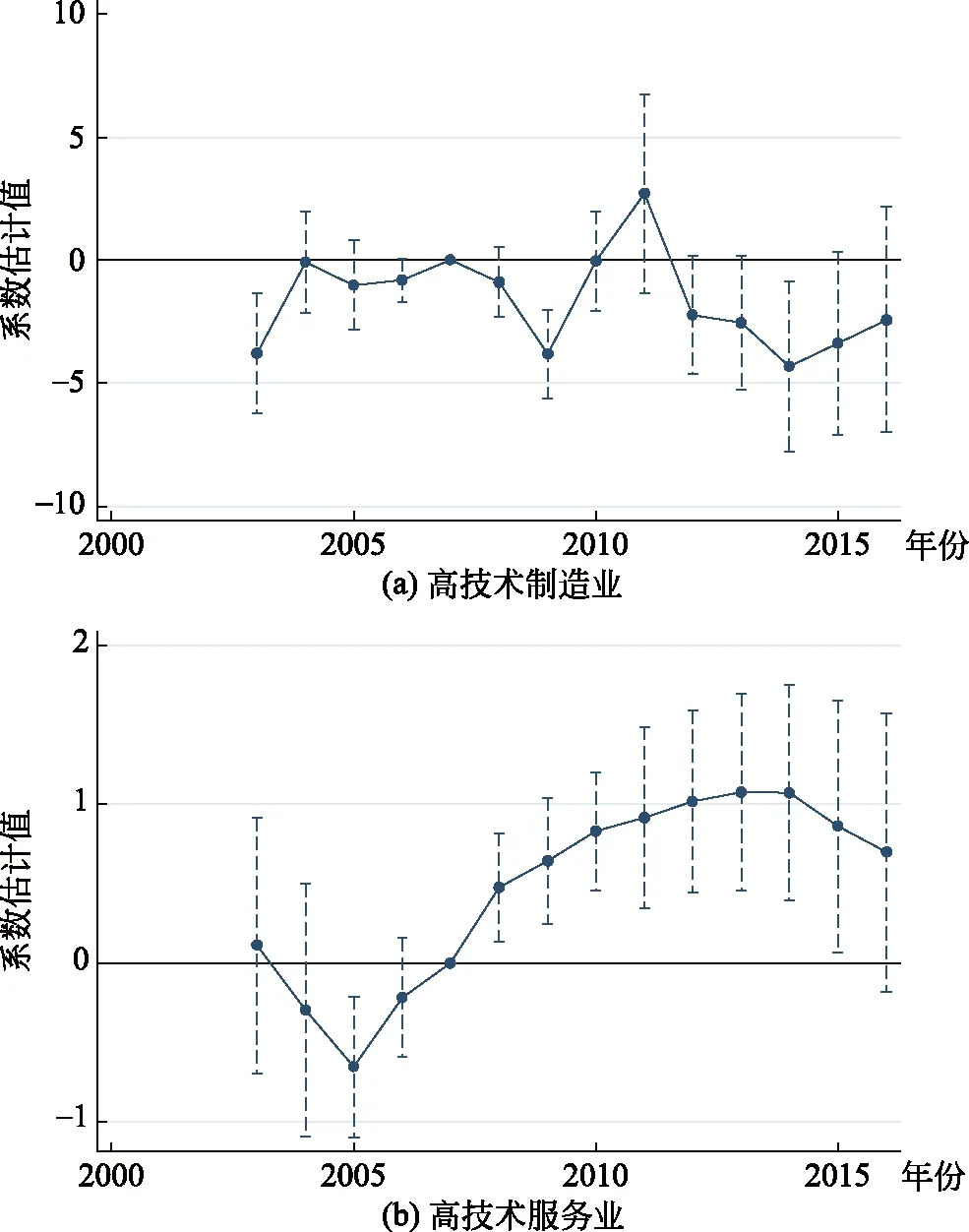
图5 高技术产业投资与冲击的关系

首先来看高技术产业投资与宏观冲击变量的关系。为此，分别以各省历年来高技术制造业投资占比和高技术服务业投资占比为因变量，利用式(6)对gshock和年份固定效应的交乘项进行回归，系数的点估计值和90%置信区间报告在图5中。(27)受数据所限，模型的估计从2003年开始。图5(a)显示，从2012年起，受冲击影响较大区域的高技术制造业投资比重与其他区域相比，有所下降，但从2014年开始这些地区在高技术制造业上的投资明显增加。从2011年前的估计结果来看，多数年份的点估计值接近于零且不显著，说明在经济增速下滑之前，各省在高技术制造业上的投资没有明显差异。

高技术服务业投资的估计结果有所不同，从图5(b)可看出，2007年前冲击效应的系数估计值多数为负，但从2008年开始，系数估计值一直为正且不断上升，到2013年达到最高点，此后开始下降。这说明相对于2007年的投资水平，受冲击影响较大区域在高技术服务业上的投资比重在2008年后一直高于其他区域，且保持递增态势。但从2014年起，区域之间的差距有所减小，这可能是由于其他区域在高技术服务业上的投资开始加速，也有可能是受冲击影响较大区域在高技术制造业上的投资增加，相应减少了在高技术服务业上的投资所致。比如，对于受冲击影响较大区域如天津，高技术制造业投资所占比重在2014年为11.5%，2015年上升到11.8%，2016年进一步升至12.7%，而高技术服务业投资所占比重2014年是4.4%，2015年则降至3.3%，尽管在2016年有所回升。对于受冲击影响较小区域如新疆，高技术制造业投资比重2014年为2.4%，2015年降到1.7%，2016年进一步降至1.5%，但高技术服务业投资的比重则从2014年的2.6%，升至2015年的2.9%，2016年进一步上升至3.3%。

以上分析表明高技术产业投资和宏观冲击关系紧密，受冲击影响较大区域近年来在高技术产业，特别是高技术制造业上的投资比重有所增加。为了进一步检验高技术产业投资对资本产出率的作用，根据模型(8)，分别估计了三次产业单位资本产出增长率和高技术产业投资的关系，结果见表4。(28)为了节省篇幅，表4中仅报告冲击效应及冲击和高技术产业投资交乘项的估计结果。其中(1)～(3)列报告了高技术制造业投资对三次产业资本产出率的影响。可以看出，加入高技术制造业投资和冲击效应的交乘项后，冲击效应系数估计值的符号没有变化，尽管其显著性有所降低。从交乘项来看，其系数在第一产业和第三产业的回归中不显著，在第二产业的估计中都为正，且在2013年和2014年两年中显著。由此可知，相对于受冲击影响较小的区域，受冲击影响较大区域的高技术制造业投资更有助于第二产业的发展，使其资本产出率得以提升。对于第一和第三产业而言，高技术制造业投资对区域间资本产出率的影响并无明显差异。

表4中(5)～(7)列报告了高技术服务业投资对三次产业资本产出率的影响。和(1)～(3)列的结果类似，冲击效应的系数在加入交乘项后符号没有变化，其中第一产业和第二产业系数的显著性也基本没有变化，第三产业系数变得不再显著。从高技术服务业投资与冲击效应的交乘项来看，在第一和第二产业的回归中不显著，在第三产业的估计中系数为正且于2014年在10%水平显著。(29)高技术服务业投资和冲击效应交互项的系数估计值明显比高技术制造业投资和冲击效应交互项的估计值要大，其原因在于高技术服务业投资所占比重和高技术制造业投资所占比重相比较小所致。比如，在2013年到2016年期间，高技术制造业投资所占比重的均值和标准差分别为11.9%和7.8%，而高技术服务业投资所占比重的均值和标准差为3.0%和1.4%。这说明高技术服务业投资对于第一和第二产业单位资本产出的增长没有显著影响，对于第三产业单位资本产出的增长有一定作用，相比于高技术制造业投资，高技术服务业投资对单位资本产出增长率的贡献较小。

总之，以上分析表明：经济增速减缓时，产品需求比如制造业产品的出口需求下降，一些厂家可能因此而倒闭，资本出现外流，所以受冲击影响较大区域的资本增长率相对降低。此时企业之间的竞争压力加剧，但投资于创新品的机会成本相对较低，因此这些区域的高技术产业投资活跃，产业结构转型升级加快，从而有助于提高其资本产出率。相比于高技术服务业，高技术制造业投资对资本产出率的影响更为明显。一个可能的解释是：我国服务业整体水平较低，尽管高技术服务业投资在2014年前不断增加，但高技术服务业对资本产出率的作用有限。(30)通常认为服务业的生产率较低，但也有研究发现借助网络技术，服务业的生产率可以大幅提高(江小涓, 2018)。另一个发现是，不管是高技术制造业投资，还是高技术服务业投资，其作用局限于行业大类内部，对其他产业的溢出效应并不明显，即高技术制造业投资仅对第二产业资本产出率有作用，而高技术服务业投资仅对第三产业资本产出率有影响。

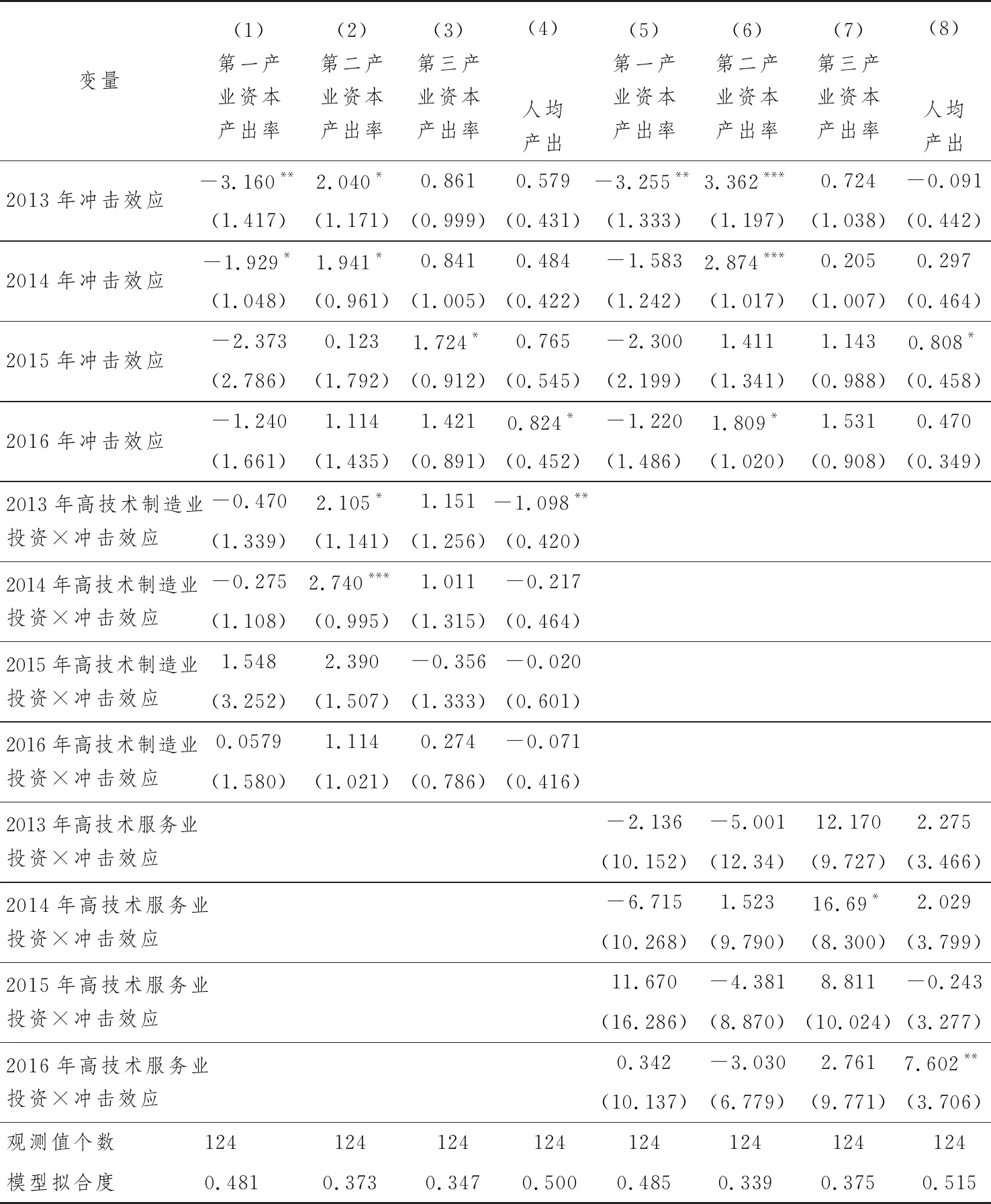
表4 高技术产业投资对单位资本产出和人均产出的影响

本文也根据模型(8)，估计了高技术制造业和高技术服务业投资对人均产出的影响。从表4第(4)列和第(8)列的估计结果可以看出，在加入交乘项后，冲击变量对人均产出的影响没有明显变化，尽管其显著性有所下降。高技术制造业投资对人均产出的作用仅在2013年显著，但系数为负，这表明受经济增速放缓冲击影响较大区域的高技术制造业投资并没有带动这些地区人均产出的增长。从高技术服务业投资的估计结果来看，其对人均产出的作用在多数年份为正，但仅在2016年显著，这说明高技术服务业投资对人均产出增长有一定贡献，但作用缓慢。对此，一个可能的解释是，受经济冲击影响较大区域的高技术产业投资虽促进了这些地区产出增加，但由于人口和劳动力从这些地区流出相比于资本较慢，所以从人均产出上来看，高技术产业投资的作用在短期并不明显；另一种可能是，受数据所限，本文没有区分各产业的人均产出，仅从总体上检验高技术产业投资对人均产出的作用，如果高技术产业投资对不同产业劳动生产率的作用不同，利用总体数据估计得出的结果可能会掩盖这种差异。

5 结论

近年来我国经济增长的速度有所放缓，从之前的年均10%降至8%以下，宏观经济的这一变化无疑会给各地带来冲击。本文提出一个分解方法，把区域产出分解为资本、就业、单位资本产出和劳均产出，在此基础上利用31个省(自治区、直辖市)2000—2016年的数据，建立了一个差分模型，通过经济增速放缓前后以及区域之间各分解变量增长率的比较，来识别宏观冲击对各区域的影响及各地的动态调节方式。为了测度冲击，本文采用Bartik(1991)的偏离份额方法，通过全国各产业增加值的增长率和冲击前各省相应产业所占比重，构造了一个能够捕捉各地所受冲击的指标。

本文研究发现宏观冲击对区域经济的影响存在明显的空间差异。与受冲击影响较小区域相比，受冲击影响较大区域的资本增长率相对较低，分产业来看，宏观冲击对第二和第三产业的影响明显强于第一产业。城镇单位就业受冲击的影响较小，但以常住人口为就业的替代变量时，其响应比较强烈。与受冲击影响较小区域相比，受冲击影响较大区域的人口，特别是外来农村劳动力在流出。相比于资本的自我调节，人口和劳动力的调节速度较慢，有一定时滞，但持续的时间较长。与资本和人口所受的负面影响不同，受冲击影响较大区域的单位资本产出，特别是二、三产业的单位资本产出以及人均产出增长率近年来显著提高，表明这些地区的生产率在经济增速放缓时得以改善。

相对于受冲击影响较小的区域，受冲击影响较大区域的资本和人口增长率有所降低，但其单位资本产出和人均产出的增长率却在提高，这似乎是一个悖论。本文运用破坏性创新和竞争压力理论对这一悖论进行了解释，并采用高技术产业投资数据对其加以验证。实证结果表明，经济增长速度放缓时，需求下降，竞争加剧，企业面临的压力增强，破产倒逼的风险加大，但投资于创新品的机会成本降低。因此受冲击影响较大的区域更倾向于增加高技术产业投资，从而促进这些地区的产品升级和产业转型，推动其生产率的提高。与高技术服务业投资相比，高技术制造业投资对区域生产率，特别是资本产出率的作用更为突出。

本文研究有助于深入理解近年来我国经济增长速度的变化。现有文献多是从宏观层面对此展开研究，本文基于空间异质性，发现经济增速放缓时各区域的响应明显不同，这为相关研究提供了一个新的视角。通过把区域产出进行分解，发现相比于劳动力，资本在区域经济的自我调节中发挥更为重要的作用，这与现有文献强调劳动力自我调节的发现不同，从而丰富了宏观冲击区域效应的相关研究。本文采用高技术产业投资数据，给出了支持破坏性创新和竞争压力理论的证据，表明尽管经济增速下降为区域经济发展带来了挑战，但也为经济结构调整和产业转型升级提供了契机。本文研究基于区域总量数据，如果能利用微观调查数据，从企业或劳动力的个体行为出发，可能会找到经济增速放缓时企业调整投资以及就业变动更为直接的证据，这是下一步研究的一个方向。此外，本文并未对宏观冲击的具体类型比如需求冲击和供给冲击进行区分；而不同冲击对区域经济的影响可能有差异，因此这是进一步研究的另一个方向。