长期增长中的最优政府间转移支付1:基于地方公共服务的跨区域溢出效应
2020-10-23金戈林燕芳
金戈 林燕芳
0 引言
自Arrow and Kurz(1970)、Chamley(1986)和Barro(1990)的开创性研究以来,关于动态最优公共支出和最优税收的研究一直是公共经济学和经济增长理论的重要研究主题。值得注意的是,这一领域的大多数研究都是在仅包含单一政府的动态模型里展开(如Turnovsky,1996)。然而,在现实世界中,除了新加坡等少数国家,绝大多数国家都包含多级政府。如美国包含联邦、州和地方三级政府;中国则包含中央、省市区、地市、县市区和乡镇五级政府。在研究动态财政问题时,如果忽略了多级政府框架,也就等于忽略了政府间的行为关系以及政府间的转移支付,而这些问题在现实中都是至关重要的。
基于以上考虑,邹恒甫、龚六堂、郭庆旺等一些学者开始将Oates(1972,1993)等人的财政分权框架引入动态财政模型,构建了包含多级政府支出及政府间转移支付的经济增长模型,进而考察了中央对地方的最优转移支付率以及转移支付率变动对经济增长的影响(Zou,1994,1996;Gong and Zou,2002,2011;郭庆旺等,2009)。
然而,上述关于政府间转移支付的动态分析,主要是从中央和地方政府由于税收种类不同而存在收入盈余或缺口的角度进行研究,而普遍忽略了地方公共服务存在跨区域溢出效应(即空间外部性)这一重要因素。
不同级次的政府存在收入盈余或缺口,虽然是世界各国实行政府间转移支付的主要原因之一,但并非唯一原因。事实上,从经济学的角度,如果不同级次政府存在收入盈余或缺口,理论上完全可以通过重新设计税制来解决,而并非必须由转移支付来解决。实践中,政府间转移支付存在的另一个(甚至是更为重要的)原因是,地方政府提供的地方公共服务对本地区以外的居民产生了跨区域溢出效应(即空间外部性)。如果没有中央政府的转移支付进行协调,这种空间溢出效应就很难得到矫正,则地方公共服务无法实现有效提供。换句话说,为了矫正这种跨区域的地方公共服务外部性,需要由中央政府通过转移支付对地方政府的行为进行干预。实际上,这也是Gordon(1983)关于最优政府间转移支付的经典研究的出发点。在Gordon的模型中,政府间转移支付的原因在于:地方公共服务对非本地居民存在着跨区域溢出效应,从而地方政府激励不足,需要中央政府通过转移支付进行干预。Oates(1999)也认为矫正地方公共服务空间外部性是政府间转移支付的一项重要职能。Bird and Smart(2002)则进一步强调,从经济学的角度,实行政府间转移支付的最重要的基础就在于存在着地方公共服务的跨区域溢出效应。
然而,Gordon(1983)的研究是在静态模型中进行的。本文试图将Gordon(1983)关于转移支付矫正跨区域空间外部性的核心思想引入Barro(1990)模型,借鉴Gong and Zou(2002,2011)的分析方法,构建一个包含中央政府、地方政府与代表性消费者的三阶段Stackelberg博弈的内生经济增长模型,引入地方公共服务的跨区域溢出效应,重点考察中央对地方的最优转移支付率、地方政府的最优财政政策及相应的最优税收。
与现有相关文献相比,本文的主要结论与贡献体现在以下几个方面。
(1) 本文在Barro(1990)的经典模型基础上引入了多级政府框架。我们借鉴了Gong and Zou(2002)的分析框架,构建了一个中央、地方和代表性消费者之间的三阶段Stackelberg博弈过程。但相对Gong and Zou(2002)的文献,我们在研究方法上有了很大的改进。具体而言,Gong and Zou(2002)只求解了消费者的动态最优化,在求解地方政府和中央政府的最优化问题时均假定经济趋于不变的稳态,因此实际上只求解了静态最优化问题。在本文中,我们借鉴并扩展了Chamley(1986)、金戈(2010)研究最优税收时使用的逆向归纳法,依次求解了三阶段博弈中消费者、地方政府和中央政府的动态最优化问题。因此,我们的模型无需收敛于一个不变的稳态;实际上,其本质上是一个内生增长模型,收敛于平衡增长路径(稳态增长),这也是我们对Barro模型的继承。根据Lucas(1990)的说法,收敛于平衡增长路径的模型更适于解释增长型经济(growing economy)。在这个意义上,本文为研究内生经济增长中的最优政府间转移支付提供了一个分析框架。
(2) 已有的研究多级政府公共支出与经济增长的文献(如Gong and Zou,2002;邹恒甫和龚六堂,2005)往往忽视了地方公共服务所产生的跨区域溢出效应,相对于此,我们在本文中明确引入了地方公共服务的跨区域外部性,探讨了中央政府如何通过转移支付矫正地方政府行为的机制,求解了中央和地方的税率函数(依赖于转移支付率),并推导了中央对地方的最优转移支付率。我们发现,中央对地方的最优转移支付率及相应的最优中央收入税率与地方公共服务对相邻地区产出的弹性系数正相关,与地方公共服务对本地区产出的弹性系数负相关。进一步,我们发现,收入税筹资模式下的次优转移支付率与总额税筹资模式下的第一优转移支付率相比,两者之间存在一个税收楔子。这一结论意味着,如果地方公共服务存在正的外部性且中央政府以收入税筹资,那么中央政府对地方政府的次优转移支付率应大于无税收扭曲时的第一优转移支付率。这一发现对转移支付政策实践具有一定的理论启示。
(3) 我们发现,当地方公共服务只对生产具有直接影响时,最优地方公共支出占产出的比例等于地方公共服务对本地区的产出弹性与对相邻地区的产出弹性之和,而且这一结论与政府采取收入税或总额税筹资无关,也就是具有税收中性的特征。相比Barro(1990)在一级政府模型里的重要发现,即无论以收入税还是总额税筹资,最优生产性公共支出与产出的比例等于生产性公共服务的产出弹性,我们的研究将Barro(1990)的发现扩展到了多级政府框架中。
(4) 当地方公共服务不仅影响生产,同时也直接增进居民效用并对相邻地区产生跨区域的消费外部性时,地方政府和中央政府的最优政策都会发生变化。特别地,我们发现,这时中央政府应该采取更高的转移支付率以及更高的收入税率。
本文的模型框架是一个包含多级政府支出与政府间转移支付的动态增长模型。这一系列文献是由邹恒甫(Zou,1994,1996)最先发起的。以下对该系列文献进行简要回顾。
Zou(1994)在一个地方政府最大化自身效用的动态模型中,最先考察了中央转移支付对地方政府公共支出的短期和长期影响。在此基础上,Zou(1996)正式构建了一个包含中央和地方两级政府的代表性消费者动态模型。其中,中央政府以收入税筹资并向地方政府实行转移支付;地方政府以消费税、收入税和中央转移支付筹资,并向社会提供地方公共消费和地方公共资本。作者发现:在长期,中央对地方公共投资的配套拨款对地方公共资本和公共消费以及私人资本和私人消费均产生促进作用;而中央对地方公共消费的配套拨款对上述变量均无长期效应;但是,如果效用函数为Arrow-Kurz型(即地方公共资本不仅影响生产,也促进效用),那么,中央对地方公共消费的配套拨款对上述变量将产生负的长期效应。
龚六堂和邹恒甫(2000,2002)、Gong and Zou(2003)在Zou(1994,1996)的模型基础上,进一步引入了中央政府提供的公共服务,假定中央公共服务和地方公共服务同时进入生产函数和效用函数。通过参数赋值,作者考察了中央和地方各税率以及中央对地方的转移支付率变动与经济增长率的数量关系,并发现,中央对地方公共投资的转移支付可以促进经济增长率,而中央对地方公共消费的转移支付则使得经济增长率下降。
Gong and Zou(2002),邹恒甫和龚六堂(2005)则进一步考察了多级政府动态模型中的最优转移支付及相应的最优税收。假定中央政府以收入税筹资,提供全国性公共服务,并向地方政府进行转移支付;地方政府以消费税、财产税以及中央转移支付筹资,并向本地居民提供地方公共服务。中央公共服务同时进入两地居民的生产函数和效用函数,地方公共服务仅进入本地居民的生产函数和效用函数。作者发现,如果消费者具有对数效用函数,生产函数为柯布-道格拉斯形式,则在最优路径上:地方财产税为零,消费税为正;中央收入税可正可负,对地方的转移支付为负。如果转移支付施加非负限制,则中央最优收入税为正,对地方的最优转移支付为零。进一步,在一个中央和地方政府均以收入税筹资的模型中,Gong and Zou(2011)得到了使增长率最大化的中央和地方收入税率,并且发现中央和地方的收入税率之和独立于转移支付率。
在龚六堂和邹恒甫的模型中,转移支付以配套拨款的形式存在。郭庆旺等(2009)则在他们的模型中假定中央对地方的转移支付是地方自有财力的一个比例,并引入了人力资本积累。假定中央和地方公共服务不仅直接促进生产,也促进了人力资本积累。他们发现,最优转移支付与财政分权水平有关。如果财政支出分权水平越高而财政收入分权水平越低,则中央对地方的最优转移支付率越高。
如前文所述,以上一系列关于政府间转移支付的动态研究均忽视了地方公共服务所产生的跨区域溢出效应。然而,在实践中,地方公共服务对本地区以外的居民存在着空间溢出效应这一现象是普遍存在的,并且已经在大量经验研究中得到验证。
早期对地方公共服务空间外部性进行验证的一项重要研究是Case et al.(1993),他们借助Anselin(1988)提出的空间计量方法,利用美国各州政府的相关数据进行经验研究,发现各州政府的公共服务支出具有显著的正向空间溢出效应,相邻地区增加1美元公共服务支出促进本地区至少增加70美分的相应支出。Schaltegger and Zemp(2003)研究显示,公共服务支出总体上没有显著的空间溢出效应,但其并无法为具体类别的公共服务支出是否具有空间溢出效应提供信息。他们的进一步研究显示公共安全支出具有明显的空间溢出效应,主要中心城市增加10%的公共安全支出,周围郊区城市的公共安全支出相应地降低3.1%,而教育、健康、文化娱乐、福利、交通、环境以及经济方面的公共服务支出没有发现明显的空间溢出效应。为了更好地识别公共服务支出的跨区域溢出效应渠道,Baicker(2005)采用不同的指标(地理相邻、人口统计学以及地区间的流动性)来度量邻近地区(Neighborliness),发现人口流动性越强的地区,其公共服务支出产生的空间溢出效应越大,这些地区的公共服务支出增加1美元能够促使相邻地区公共服务支出相应地增加接近1美元。Ermini and Santolini(2010)基于意大利马尔凯大区的市镇截面数据,也发现各地区间的公共服务支出存在明显正向空间溢出效应,不仅公共服务支出总量上具有显著的空间溢出效应,而且还体现在各类不同的具体公共服务支出上。基于地方政府公共服务支出空间溢出效应的存在,Lpez et al.(2017)利用西班牙市级层面数据,进一步对福利、环境、教育、文化等十类公共服务支出的跨区域溢出效应的途径及作用方向进行研究。
还有一些学者关注特定公共服务支出的空间溢出效应。Holtz-Eakin and Schwartz(1995)首先利用美国相邻州的数据研究高速公路对相邻地区生产率的空间溢出效应。Boarnet(1998)在他们的研究基础上,利用美国加州县级数据并构建多种空间权重矩阵进行实证分析,发现街道和高速公路公共基础设施对相邻地区的产出具有负的空间溢出效应,他给出的解释是:完善的基础设施使本地区具有区位优势,吸引相邻地区的经济资源和生产要素流入本地区,进而抑制了相邻地区的经济增长。另一方面,Cohen and Morrison(2004)、Bronzini and Piselli(2009)分别根据美国和意大利相关数据的研究指出,基础设施通过降低相邻地区的运输成本和交易费用从而促进相邻地区的经济增长,即基础设施对相邻地区的经济增长产生正的空间溢出效应。考虑到空间绿化不仅能够提高生态服务增加居民的娱乐效益,同时也是各地区争夺高端人才和企业的战略之一,Choumert and Cormier(2011)利用法国市级层面的城市公园支出情况进行实证分析,发现各地区在城市公园绿化支出上具有正向关系,相邻地区在城市公园方面的支出增加10%,会促使本地区在城市公园方面的支出会相应地增加3.6%。
作为发展中大国,中国的发展经验也为地方公共服务空间溢出效应的存在提供了大量证据。邵军(2007)沿着Case et al.(1993)的思路,根据2001—2005年中国各省市相关变量的平均数值通过空间计量方法研究表明,中国地方公共支出具有显著的正空间外部性,即提高某地区的公共支出会促进其他地区公共支出的增长。进一步,一些学者对公共支出的各具体分类项目的空间溢出效应进行了研究。其中,郭玉清等(2012)将公共支出分为基本建设、文教科卫、行政管理、预算外四个部分进行研究,结果显示基本建设和文教科卫具有显著空间溢出效应;罗丽英和刘柳(2015)利用省级面板数据,选取对基础设施、环境、医疗、教育等方面的公共产品进行实证研究,结果显示不同类型的公共产品对经济增长的空间溢出效应存在差异。胡鞍钢和刘生龙(2009)、刘秉镰等(2010)等利用中国交通运输投资的相关数据进行实证研究,发现铁路、公路等公共服务存量的增加提高了其他地区的全要素生产率,从而促进了其他地区的经济增长。Xie et al.(2016)基于中国城市层面数据,研究交通基础设施对城市环境的空间溢出效应,发现交通基础设施对相邻地区的环境具有负向效应,而一个地区的技术进步对相邻地区的环境质量具有正向空间溢出效应。张浩然和衣保中(2012)将关注点拓宽到通讯基础设施和医疗条件,基于中国城市面板数据进行实证分析,发现通信基础设施和医疗条件不仅提高了本地区的全要素生产率,同时还对邻近城市产生显著的正向空间溢出效应。此外,Deng et al.(2012)利用城市截面数据,发现增加环境保护方面的公共服务支出会减少相邻地区相应公共服务支出。
如上所述,中国经验研究和国外经验研究都证实了地方公共服务对相邻地区存在显著的空间溢出效应。因此在研究动态最优政府间转移支付时,有必要引入这种地方公共服务的跨区域外部性。这也正是本文所要解决的问题。
本文余下部分安排如下:第1部分介绍基本模型的设定,阐明中央、地方和代表性消费者的三阶段Stackelberg博弈过程,求解分散均衡中代表性消费者对中央和地方政策变量的反应函数(消费函数)和间接效用函数。第2部分利用代表性消费者的间接效用函数,逆向求解地方政府对中央政策变量的财政政策函数,并解出模型的经济增长率(作为中央政策变化的函数)。第3部分首先论证模型中福利最大化与增长最大化的一致性,求解次优配置中的中央对地方最优转移支付率及相应的最优中央收入税率,进而解出地方最优公共支出水平及地方最优收入税率等一系列变量。第4部分是模型扩展,探讨地方公共服务在促进生产的同时也直接影响居民效用的情形。最后一个部分是简要的总结与进一步研究展望。
1 基本模型
1.1 环境
假定经济中存在着两个相邻地区,分别由两个地方政府进行管辖。每个地方政府分别向本地居民提供生产性公共服务。每个地区的生产性公共服务不仅促进了本地区生产活动,也对相邻地区的生产活动产生了跨区域外部效应。在两个地方政府之上还存在着一个协调地区间事务的中央政府。
每个地区均有一个无限存活的代表性消费者(居民)。假定两个地区的代表性消费者具有相同的偏好,其跨期效用函数形式为:
(1)
其中,σ>0为消费者相对风险规避系数,ρ>0为时间偏好系数,ci表示i地区代表消费者的个人消费,t为时间。下标i表示地区,i∈{1,2}。代表性消费者在给定中央和地方政府政策变量及自身预算约束的条件下,通过选择个人消费路径以最大化一生总效用。为了简化,我们假定资本折旧率为0,则消费者的预算约束(人均资本积累方程)为:
(2)
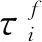
每个代表性消费者各自经营一家代表性企业,生产函数形式为:
yi(t)=Aki(t)αgi(t)βg-i(t)γ
(3)
其中,gi和g-i分别表示本地政府和相邻地区政府提供的生产性公共服务;A>0为技术系数;α∈(0,1),β∈(0,1)和γ∈(-1,1)分别为资本、本地区公共服务和相邻地区公共服务的产出弹性;假定α+β+γ=1,即生产函数具有一次齐次性质。特别需要指出,弹性系数γ代表了相邻地区公共服务对本地区生产活动的跨区域溢出效应。当γ=0时,不存在公共服务的跨区域外部效应;当γ>0,则存在正的空间溢出效应;当γ<0时,则存在负的溢出效应。
中央政府的目标是两个地区的整体社会福利最大化。则中央政府的目标函数为:
(4)
其中,χ和(1-χ)分别为中央政府赋予地区1和地区2的权数。我们假定两个地区的消费者效用对中央政府同等重要,即χ=1/2。中央政府以收入税融资,并向两个地方政府分别实行转移支付,在任意时间t的预算约束为:
(5)
其中,-1<υi<1(i=1,2)表示中央对第i地区的转移支付比率(配套率)。为了矫正地方公共服务的空间外部性,中央政府对地方政府实行配套转移支付(正向或逆向)。
地方政府则通过向本地居民提供公共服务以最大化本地区代表性消费者效用,其收入来源包括地方收入税和来自中央政府的转移支付。这样,地方政府的平衡预算约束为:
(6)
地方公共服务由地方政府和中央政府(通过转移支付)共同承担,即:
gi(t)=[1-υi(t)]gi(t)+υi(t)gi(t)
其中,地方政府负担[1-υi(t)]gi(t),中央政府通过转移支付承担υi(t)gi(t)。如果地方政府在公共服务投入1元,则中央政府出资υi/[1-υi]元。反过来说,中央政府可以通过合理设置υi使得地方政府选择最优的投入水平。
地方政府面临的本地区资源约束为:
(7)
注意,将两个地区的资源约束加总,并结合中央政府预算约束式(5),就蕴含了两个地区的总社会资源约束:
(8)
根据模型中生产函数和效用函数的设定,经济的最优配置将从初始状态开始就进入稳态增长,即沿着一条平衡路径增长。
为了将本文的研究重心集中于考察地方公共服务的空间外部性及中央政府如何通过转移支付矫正这种空间外部性,本文忽略了中央政府提供的全国性公共服务,也没有考虑消费性公共服务。但需要指出,以本文的模型为基础,我们可以很方便地引入中央的全国性公共服务,也可以将全国或地方的公共服务引入效用函数,而且这些步骤不会对本文关于最优政府间转移支付的结论产生实质性影响。
1.2 三阶段Stackelberg博弈的次序及求解过程
中央政府、地方政府和代表性消费者之间形成一个典型的三阶段Stackelberg博弈,博弈次序如下:
第一阶段,中央政府宣布中央收入税率的时间路径及对两个地方政府公共服务的转移支付率(配套率)路径。
第二阶段,两个地方政府在给定中央政府政策变量的前提下,进行同时博弈(Cournot博弈),各自选择并宣布本地区的收入税率路径和地方公共服务路径。
第三阶段,两个地区的代表性消费者在给定中央和两个地方政府的政策变量及初始条件下,各自选择自身的消费(及投资)路径。
上述博弈的求解方法为逆向归纳法。即首先求解两个地区代表性消费者的效用最大化问题(即分散均衡),得到消费者的消费函数(对中央和地方政策变量的反应函数)和间接效用函数;其次求解两个地方政府的本地福利最大化问题,得到地方政府的最优财政政策(对中央政策变量的反应函数);最后求解中央政府的整体福利最大化问题,得到中央政府的最优转移支付率及相应的中央收入税率。
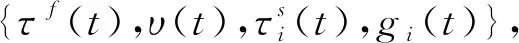
1.3 分散均衡
每个地区的代表性消费者分别在给定中央政府、本地区政府及相邻地区政府的政策变量及个人预算约束式(2)下,通过控制个人消费路径,以最大化其一生总效用式(1)。其汉密尔顿函数为:
(9)
其中,qi为汉密尔顿乘子。求解一阶条件,得到:
(10)
结合式(9)和式(10),我们得到个人消费的增长率(欧拉方程):
(11)
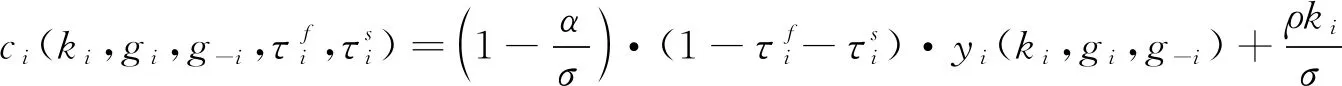
(12)
进而将式(12)代入式(1),我们就得到了代表性消费者的间接跨期效用函数:
(13)
其中,
(14)
2 地方政府的最优政策函数
两个地区的地方政府均在给定中央政府政策变量和相邻政府公共服务水平的前提下,最大化本地代表性消费者的间接跨期效用函数式(13),受约束于本地区资源约束式(7)和自身平衡预算约束式(6),其汉密尔顿函数为:
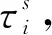
结合(15)和(16)两式,我们得到:
(17)和(18)两式非常重要,它们给出了两个地方政府的最优财政政策函数(作为对中央收入税率和转移支付率的反应函数),我们总结为以下的命题。
命题1
在以收入税筹资的两级政府的框架里,地方政府的最优地方公共支出(以公共支出与产出的比例衡量)函数为:
相应的最优地方收入税率函数为:
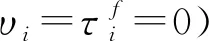
但是,只要当地方公共服务对相邻地区存在溢出效应(即γ≠0)时,地方政府仅根据地方公共服务对本地区的产出弹性来选择地方公共支出水平gi/yi=β是没有效率的。因此,需要中央政府通过转移支付进行干预。根据命题1,我们发现,中央收入税率降低了地方公共支出水平,这是因为中央收入税率降低了地方收入税率;但同时,中央对地方的转移支付率提高了地方公共支出水平。因此,中央政府需要面临的问题是,如何设计最优的转移支付率和中央收入税率,使得地方公共支出达到最优水平。
直觉上可预见的是,如果不存在税收扭曲,中央政府对地方政府的最优转移支付率为:γ/(β+γ),即最优转移支付率等于公共服务对相邻地区的产出弹性(外部性系数)与公共服务对本地及相邻地区的产出弹性之和的比值;但是,收入税降低了私人资本的收益率,扭曲了行为人的跨期决策。因而,在一个动态框架里,收入税的存在使得最优转移支付率将发生变化,而具体会发生怎样的变化是无法预见的。关于税收扭曲将会如何影响最优转移支付率的问题,本文将在第3部分进行探讨。
根据模型设定,两个地区从初始状态开始就进入平衡增长路径。经济增长率由φi表示。根据式(11)~(12)以及式(18),我们可以分别解出地区产出、消费与地区资本存量的比例:
进一步,根据式(17)和式(19),并利用生产函数式(3),我们得到本地区地方公共支出以及相邻地区地方公共支出与本地区资本存量的比例:
注意,根据模型设定,两个地区的消费者偏好和生产技术是相同的,且初始资本存量相同。因此,两个地区本质上是同质的,中央政府对两个地区的收入税率和转移支付率必然是相同的,两个地区的产出、消费、地方公共支出、税收以及经济增长率也必然是相等的。(3)假定两个地区同质,并不会抵消相互之间的正向或负向空间外部性。以正外部性为例,假定两个地区的公共服务相互存在正向溢出效应,那么,如果没有中央政府的干预,每个地区的公共服务都是不足的。因此,同质假定对本文而言,只是一种研究上的便利,不会对研究结论产生实质性影响。
从而,我们必然有gi/ki=g-i/ki。这样,通过联立方程式(21)和式(22),我们解出两个地区的经济增长率:
(23)
从这里开始,为了行文的方便,如无特殊情况,我们均去掉代表地区的下标i。
3 中央政府的最优转移支付与收入税率
3.1 中央的最优化问题
中央政府面临的问题是,根据两地区地方政府及代表性消费者的决策函数(反应函数),在其自身预算约束条件下选择对地方政府的转移支付率及相应的中央收入税率以最大化整体社会福利式(4)。
根据式(20),我们得到
(24)
将式(24)和k(t)=k(0)eφt代入式(4),并利用χ=1/2,得到:
(25)
其中,ρ>φ(1-σ)以保证跨期效用有界。
根据式(25),整体社会福利水平W是经济增长率φ的函数。经过推导,我们发现:(4)不等式(26)的证明见附录2。
(26)
式(26)意味着,整体社会福利最大化等价于地区增长率最大化。因此,中央政府的整体社会福利最大化问题转化为在自身预算约束式(5)下最大化地区增长率式(23)。
由于两个地区是同质的,中央政府的预算约束式(5)可简化为τfy=υg。进一步,利用式(17),我们将中央预算约束改写为:
(27)
式(27)实际上给出了中央政府的收入税率函数。结合式(18)可知,中央收入税率、地方收入税率,以及两者之和,均为转移支付率υ的函数。
为了求解最优转移支付率,我们将式(27)代入式(23),得到:
(28)
这样,中央政府的问题就进一步转化为:通过选择转移支付率υ以最大化式(28)。最大化的一阶必要条件为:
(29)
根据模型参数设定,转移支付率υ∈(-1,1),则必然有:
因此,要使一阶条件式(29)成立,则要求γ-)γ+αβ(υ*=0。这样,我们就可以得到:
(30)
可以证明,υ*是φ(υ)在定义域(-1,1)上的唯一全局最大值解。(5)关于υ*是φ(υ)唯一全局最大值解的证明见附录3。也就是说,υ*是唯一的最优转移支付率。
进一步,将式(30)代入中央预算约束式(27),得到最优的中央收入税率:
(31)
式(30)和式(31)分别给出了中央政府的最优转移支付率及相应的最优中央收入税率,是本文的核心结果,我们将其总结为命题2。
命题2
在以收入税筹资的两级政府的框架里,中央政府的最优转移支付率为:
相应的最优中央收入税率为:
命题2是本文的核心结论,给出了当两级政府以收入税筹资时,中央政府对地方政府的最优转移支付率和相应的最优中央收入税率。为了进一步理解这一命题背后的经济学含义,我们首先来考虑一下当两级政府以总额税筹资时的情形。由于总额税是没有扭曲性的,因而当中央和地方政府以总额税筹资时,分散均衡能够复制社会最优(第一优)配置。我们从直觉上可以预见,在社会最优(第一优)配置中,中央政府对地方政府的最优转移支付率为(本文的附录1给出了严格证明):
(32)
式(32)的经济意义很容易理解。由于存在地方公共服务的跨区域外部性,在没有中央政府干预时,地方政府所提供的地方公共服务水平是没有效率的。根据生产函数式(3),地方公共服务对本地经济的产出弹性系数为β,对邻近地区的生产外部性系数是γ。因此,在没有税收扭曲的前提下,中央政府对地方政府进行一项比例为γ/(β+γ)的转移支付(相当于庇古补贴或庇古税),可以矫正地方政府的行为。
然而,当中央政府以收入税为转移支付筹资时,税收对行为人的跨期选择带来了扭曲。在次优配置中,最优转移支付(实际是次优转移支付,即the second-best optimal intergovernmental transfers)必须考虑到这种税收所带来的扭曲。当γ≠0时,通过将式(30)和式(32)两式相除,并利用式(31)的结论,我们可以得到:
(33)
式(33)告诉我们,当政府以收入税筹资时的次优转移支付率与当政府以总额税筹资时的第一优转移支付率之间存在一个税收楔子,这个税收楔子等于以外部性系数度量的中央收入税单位税率。显然,这个税收楔子是由于收入税扭曲导致的。中央收入税率越高,这个税收楔子也就越大。
综合式(32)和式(33),我们可以把式(30)改写为:
(34)
上式意味着,当中央政府以收入税为转移支付筹资时,最优转移支付需要承担两个职能。一方面,最优转移支付用于矫正地方公共服务的外部性,即式(34)等号右边的第一项;另一方面,最优转移支付用于部分补偿收入税率带来的扭曲,也就是中央政府收入税率越高,中央给予地方的转移支付率也就是越高,即式(34)等号右边的第二项。
下面,我们进一步考察最优转移支付率υ*及相应的最优中央收入税率τf*与参数之间的关系。由于α+β+γ=1,任何一个系数的变化都会引起其他两个系数的联动。考虑到我们真正关心的是地方公共服务对本地区及相邻地区产出弹性系数(即β和γ),我们固定住α,重点考察β和γ变动对最优转移支付率和中央收入税率的影响。给定α不变,我们很容易通过观察式(30)和式(31)发现,随着γ上升(β下降),最优转移支付率和中央收入税率均提高;反之,随着β上升(γ下降),最优转移支付率和中央收入税率均下降。
此外,特别注意的是,当γ<0时,则υ*<0,τf*<0。这意味着,当存在地方公共服务的负外部性时,中央应该通过负向转移支付(即地方政府向中央进行政府转移)来矫正负外部性,同时中央政府通过负所得税(即向地方无条件转移支付)以保证地方实现预算平衡。这说明,我们的理论本身不仅可以为正空间外部性,也可以为负空间外部性提供了一个矫正方案。
3.2 基于中央最优转移支付的地方最优财政政策
进一步,我们将式(30)和式(31)代入地方政府的最优财政政策函数式(17)和式(18),就得到了基于中央最优转移支付政策下的地方政府最优财政政策,如下:
我们将上述结果总结为命题3。
命题3
在以收入税筹资的两级政府的框架里,给定中央政府执行最优转移支付和最优收入税政策,地方政府的最优公共支出(以公共支出与产出的比例衡量)为:
相应的最优地方收入税率为:
命题3的经济含义很容易理解。根据式(35),最优地方公共支出占产出的比例等于地方公共服务对本地区的产出弹性β与对相邻地区的产出弹性γ之和。注意,我们在分析命题1时已经指出,如果没有中央干预,地方政府选择的公共支出—产出比例为β,而没有考虑本地公共服务对相邻地区的外部性,显然这个结果是没有效率的。现在,在中央政府的最优转移支付和收入税政策干预下,地方政府在决策时将本地公共服务对相邻地区的外部性也考虑了进去,中央转移支付使得这种跨区域溢出效应完全内部化了。
地方收入税率则需要和中央收入税率合在一起来理解。我们加总式(31)和式(36),得到:
(37)
上式告诉我们,最优时,中央收入税率和地方收入税率之和等于地方公共支出与收入的比例。对于社会而言,总的收入税率刚好等于公共支出对收入的占比,等于本地区和相邻地区公共服务的产出弹性之和。
此外,容易证明,当中央和地方政府均以总额税筹资,即不存在税收扭曲时,最优地方公共支出与产出的比例为(详细的证明参见附录1):
(38)
通过比较式(35)和式(38),我们发现最优地方公共支出与产出比例具有税收中性的特征,即这一比例与政府部门采取总额税筹资还是收入税筹资是不相关的。
Barro(1990)的研究表明,在一级政府的框架里,无论在政府以收入税筹资的次优配置中,还是在政府以总额税筹资的第一优配置中,最优生产性公共支出与产出的比例均等于生产性公共服务的产出弹性。我们的这一发现,实际上进一步将Barro(1990)关于最优生产性公共支出的税收中性结论扩展到了多级政府框架中。
3.3 地方政府Cournot博弈产生配置扭曲了吗?
比较命题1和命题3可知,当地方公共服务存在空间溢出效应时,如果没有中央政府干预,则地方政府基于本地福利最大化选择的地方公共服务水平低于最优水平。这实际上由于在Cournot博弈环境中,地方政府之间采取非合作策略引起的配置扭曲。为了进一步说明这一点,下面我们考察两个地方政府采取合作模式,即完全协调选择,如同一个地方政府行事的情形,并对比合作情形中的地方政府最优策略与非合作博弈时所采取的策略之间的差别。
此时,代表性消费者的消费函数、间接跨期效用函数分别同式(12)~(14)一致。同时,由于两个地区本质上是同质的,其产出、消费、地方公共支出以及税收必然是相等的,又由于两个地方政府的政策行为完全协调如同一个地方政府行事,此时模型退化为只有一个地方政府的两级政府模型,则代表性企业的生产函数可以由式(3)简化为:
y(t)=Ak(t)αg(t)β+γ
中央政府面临的预算约束及总社会资源约束分别由式(5)和式(8)退化为:
给定中央政府的策略,地方政府的预算约束及面临的社会资源约束分别同式(6)和式(7)一致,即为:
这样,地方政府面临的汉密尔顿函数为:
Hs=v(k,g,τf,τs)+λ[(1-τf)y-c-(1-υ)g]+μ[τsy-(1-υ)g]
其中,λ和μ分别是地方政府面临的社会资源约束和预算约束的乘子。通过求解关于τs和g的一阶条件,并结合预算约束条件进行化简,得到地方政府的最优策略函数为:
与非合作博弈时的地方最优政策函数式(17)和式(18)相比,当两个地方政府共同协调决策时,地区之间的公共服务溢出效应内部化了,给定中央政府的政策选择,地方政府的公共支出和税收决策均取决于公共服务的总产出弹性(即β+γ)。
此时,代表性消费者的消费函数(反应函数)可写成:
这样,中央政府面临的汉密尔顿函数为:
Hf=v(k,g,τf)+θ(y-c-g)+ξ(τfy-υg)
其中,θ和ξ分别为中央政府面临的社会资源约束和预算约束的乘子。结合社会资源约束及预算约束,求解最优化的一阶条件,可以得到中央的最优收入税率及最优转移支付率:
相应地,地方政府的最优收入税率和最优公共支出水平(相对于产出)分别为:
因此,当地方政府之间能够进行协调合作时,无需中央政府的干预,地方政府就能通过自身的税收政策为最优地方公共支出筹集相应的资金。而当公共服务存在空间溢出效应且各地方政府间独自进行政策选择(即非合作博弈)时,地方政府的收入税率函数为(如式(18)所示):
τs=β(1-τf)
如果中央政府不加以干预(即τf=υ=0),则地方政府选择的税率和公共支出水平(相对于产出)分别为:τs=g/y=β<β+γ。说明在非合作博弈的情形中,如果没有中央政府的干预,地方政府将选择较低的公共服务水平,导致配置扭曲。这种扭曲是由于地方政府之间采取非合作策略导致的。在中央政府的最优转移支付政策干预下,地方政府的税率为:
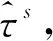
3.4 最优干预政策与不干预政策的效果比较
下面,我们在非合作博弈状态下,进一步比较中央政府采取最优转移支付政策和采取不干预政策两种状态下的社会福利水平。我们所关心的问题是,地方公共服务的空间溢出效应强度(即外部性系数γ)与中央政府的不干预政策造成的福利损失之间存在什么关系?
根据式(25)和式(26)可知,社会福利W与经济增长率φ正相关。因此,比较两种状态下的社会福利,等价于比较两种状态下的经济增长率。
如果中央政府采取不干预政策,则υ=0,将其代入式(28),我们就得到了在没有中央干预状态下的经济增长率:
(39)
如果中央政府采取最优转移支付政策,则υ=υ*,我们将其代入式(28),得到在中央政府最优转移支付下的经济增长率:
(40)
为了比较φ(υ*)与φ(0)的关系,我们需要考虑以下三种情形。
情形1:γ=0。
这时,地区间不存在公共服务的跨区域溢出效应,根据式(30),易得υ*=0。从而,必然有φ(υ*)=φ(0)。这时,中央采取最优转移支付政策等价于采取不干预政策。
情形2:γ>0。
这时,地方公共服务存在正的跨区域外部性,根据式(30),可知υ*>0。由于υ*是φ(υ)的唯一全局最大值点,则必然有φ(υ*)>φ(0)。这是意料之中的,当存在公共服务的跨区域正外部性时,相对于采取不干预政策,中央政府采取最优转移支付政策提高了经济增长率,进而增进了社会福利。
下面,我们重点分析外部性系数γ变动所带来的影响。可以证明,当γ>0时,给定α不变,以下不等式成立:(6)不等式(41)的证明见附录4。
(41)
即地方公共服务的空间溢出效应γ越大,中央政府采取最优转移支付政策相对采取不干预政策下的经济增长率差异越大;相应的,中央政府采取不干预政策的福利损失也就越大。换句话说,γ越大,中央政府采取最优转移支付政策带来的增长率增量和社会福利增量也就越大。
情形3:γ<0。
γ<0的分析与γ>0的分析完全对称,此处不再赘述。
3.5 最优平衡增长路径
给定中央政策采取最优转移支付(相应的最优中央收入税)政策,地方政府基于中央转移支付政策执行最优地方财政政策,则整个经济从初始状态开始,就进入最优平衡增长路径。消费、资本、地方公共支出以及产出的增长率均由式(40)给出。进一步,根据式(3),式(35)和式(20),可以分别得到产出、地方公共支出和私人消费与资本的最优比例,如下:
上述配置是在中央和地方政府征收收入税筹资模式下得到的最优解。如前所述,由于收入税带有扭曲,因此上述结果实际上是一种次优配置。在附录1,我们进一步考察了社会第一优配置及其在分散化决策的经济中的实现可能性。
4 扩展模型
在基本模型中,地方公共服务只对企业的生产具有直接影响。然而,现实中的公共服务往往不仅影响生产,也直接增进了居民的效用水平(如高速公路)。下面,我们对基本模型进行扩展。借鉴Gong and Zou(2011)的处理方法,我们假定地方公共服务同时进入企业生产函数和居民的效用函数。我们还假定地方公共服务不仅影响本地居民的效用,也对相邻地区居民的效用产生正的跨区域溢出效应。
这样,i地区代表性消费者的瞬时效用函数由式(1)转变为:
其中,等式右边第一项表示消费者通过消费私人产品获得的效用,第二项表示消费者通过使用当地政府提供的地方公共服务获得的效用,第三项表示相邻地区公共服务对本地居民的溢出效应。ζ,δ>0为公共服务的系数,分别表示本地公共服务和相邻地区公共服务对本地居民效用水平的影响强度。
给定中央政府和地方政府的政策选择,代表性消费者在自身预算约束式(2)条件下,通过选择个人消费路径最大化一生效用,得到的私人消费函数同式(12),即:
这样,消费者的间接瞬时效用函数为:
两个地方政府均在给定中央政府及相邻地方政府政策选择的前提下,最大化本地代表性消费者的间接跨期效用函数,其汉密尔顿函数为:
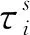
此时,给定中央政府的政策选择,地方政府的最优税率及最优公共支出水平均大于公共服务仅具有产出效应时的值(如基本模型式(17)~(18)所示),最优税率的差值取决于以产出衡量的公共服务对当地居民的效用贡献大小。同时,地方公共服务对本地居民生活水平的改善力度越强,地方政府的最优税率及最优公共支出水平也越大。
由于两个地区是同质的,结合中央政府的预算约束(同式(5))以及地方政府最优税率,可得到:
(45)
在扩展模型中,地方公共服务不仅对相邻地区的生产活动产生了正外部性,也对相邻地区的消费活动产生了正外部性,因此,相对于基本模型,地方公共服务的空间外部性增强了。进而,我们可以预见,这时的最优转移支付率υ**必将大于基本模型中地方公共服务对其他地区只具有生产外部性时的最优转移支付率υ*,即:
υ**>υ*.
进一步,通过比较式(45)和式(27),我们发现,扩展模型中的最优中央税率τf**也必然大于基本模型中的最优中央税率τf*,即:
τf**>τf*
简言之,在扩展模型中,由于地方公共服务不仅影响生产,同时还直接影响居民效用,并且对相邻地区产生正的跨区域消费外部性,因此,相对于地方公共服务仅具有生产性的基本模型,要求中央政府征收更高的收入税率并对地方政府实行更高的转移支付率。这是扩展模型的一个重要政策含义。
5 总结
本文构建了一个包含中央政府、地方政府与代表性消费者的三阶段Stackelberg博弈的内生经济增长模型,通过引入地方公共服务的跨区域空间溢出效应,探讨了中央对地方的最优转移支付率、地方政府的最优财政政策及相应的最优税收。
我们重点考察了假定地方公共服务具有生产性,并对相邻地区产生跨区域的生产外部性的基本模型,求解了收入税筹资模式下的次优配置,在逆向推导地方政府对中央政策变量的财政政策函数的基础上,论证了福利最大化与增长最大化的一致性,分析了次优路径上中央对地方的最优转移支付率及相应的最优中央收入税率,进而解出地方政府的最优公共支出水平与最优地方收入税率。我们发现:(1)中央对地方的最优转移支付率及相应的最优中央收入税率与地方公共服务对相邻地区产出的弹性系数正相关,与地方公共服务对本地区产出的弹性系数负相关;(2)次优转移支付率与第一优转移支付率之间存在一个税收楔子,该税收楔子等于以地方公共服务外部性系数度量的中央收入税单位税率;(3)最优地方公共支出与产出的比例等于地方公共服务对本地及相邻地区产出弹性系数之和,并且这一结论与政府采取收入税或总额税筹资无关。
进一步,我们在扩展模型中考察了当地方公共服务不仅影响生产,同时也直接增进居民效用并对相邻地区产生跨区域消费外部性的情形,探讨了中央和地方政府的最优政策选择与基本模型中相应政策的差异。特别地,我们发现,在这种情形中,相对于基本模型,中央政府应该征收更高的收入税率并对地方政府实行更高的转移支付率。
本文在地方公共服务具有跨区域溢出效应的视角下,提供了一个关于最优政府间转移支付的标准动态分析框架。基于本文的分析框架,我们有四个重要的扩展方向。
(1) 引入多种类型公共服务,并允许不同类型的公共服务具有不同的外部性系数。这里的重点是,我们可以允许正的外部性系数和负的外部性系数同时存在,这样,我们就可以在这个扩展框架里研究中央政府如何通过转移支付同时解决地方政府之间的正外部性和负外部性问题。
(2) 借鉴Golosov et al.(2003)、Kocherlakota(2005,2010)等人关于新动态财政学的研究,在多级政府框架中引入行为人的异质性和非线性税收结构,探索动态最优转移支付率可能存在的非线性特征。
(3) 本文对最优政府间转移支付率以及相应的经济增长率和社会福利水平进行了定性研究,在下一步的研究中,我们需要根据中国的实际情况进行参数校准,进而计算得到更为准确和更具可操作性的最优转移支付率,为实践中的政府间转移支付体系提供有价值的理论指导和评价标准。
(4) 借鉴现有的财政分权理论,在我们的多级政府动态分析框架中,引入不对称信息和地方政府竞争,引入不同的博弈次序,假定中央政府和地方政府具有不同于福利最大化的目标(比如中央政府目标可能是促进不同地区之间经济协调发展,地方政府的目标有可能是最大化本辖区内的经济增长率或财政收入),从而获得更为丰富更具现实意义的研究结果。
附录
附录1 第一优配置及其可实现性
在附录1,我们通过在基本模型中求解命令经济中的社会计划者问题得到第一优配置;并将其作为参照系,与收入税筹资模式下的次优配置进行比较,考察两者之间的差异;进而对在分散化决策的经济中实现第一优配置的可能性进行讨论。
附录1.1 第一优配置: 社会计划者问题
我们考虑一个命令经济。经济中存在一个全知全能的社会计划者,其目标是:在总社会资源约束式(8)和初始条件下,通过直接配置各种数量(消费,投资和公共支出),以最大化整体社会福利式(4)。此外,我们仍然假定,社会计划者赋予两个地区的权数是相同的,即χ=1/2;两个地区初始资本存量相同,即k1(0)=k2(0)。
这样,社会计划者的汉密尔顿函数可以写为:
其中,θ为社会资源约束的乘子(资本的社会价值)。
通过求解一阶条件,我们得到如下第一优配置:
经济从初始状态开始就进入社会第一优的平衡增长路径,两个地区的资本,产出,私人消费和公共支出均按第一优的经济增长率增长。第一优增长率为:
(49)
附录1.2 第一优配置与次优配置的比较
我们将第一优配置及其增长率式(46)~(49)与次优配置及其增长率式(42)~(44)和式(40)进行比较,不难看出,在第一优和次优配置中,公共支出与资本的比例是相同的;相应地,产出-资本比例也是相同的。但是,相对于第一优配置中,在次优配置中,消费者选择了更高的消费-资本比例以及更低的经济增长率。
导致次优配置出现扭曲的原因是收入税扭曲了资本回报率。这一点也可以通过观察均衡增长率式(11)得到。均衡增长率等于税后的资本边际产出减去时间偏好系数ρ再除以风险规避系数σ。显然,中央和地方征收收入税使得资本边际产出下降进而降低了经济增长率。
从作用机制来看,在一个动态经济中,代表性消费者面临着如何在当前消费与投资(未来消费)之间进行选择的问题。收入税的存在降低了消费者的投资回报率,从而扭曲了消费者的消费—投资决策,使得消费者倾向于选择相对较高的消费和较低的投资(以占资本存量的比例来衡量)。
附录1.3 实现第一优配置的可能性
既然次优配置的效率低于第一优配置,那么,一个自然而然的问题是:有没有可能在分散化决策的经济中实现第一优配置?
如前所述,次优配置的扭曲是由收入税导致的。如果在分散经济中,政府只能以收入税或其他扭曲性税收工具为公共支出和转移支付筹资,那么分散均衡必然将带有扭曲,只能实现次优解。
因此,为了在分散市场中实现第一优配置,需要扩大政府的税收工具集。众所周知,总额税(lump sum taxes)是没有扭曲的税收。可以证明,如果允许中央政府和地方政府以总额税而非收入税筹资,那么分散经济可以实现第一优配置。下面,我们来证明这个结论。
由于改以总额税筹资,则中央政府预算约束式(5)变为:
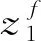
zf(t)=υ(t)g(t)
(50)
与此同时,地方政府面临的预算约束式(6)变为:
[1-υ(t)]g(t)=zs(t)
(51)
其中,zs表示地方政府对本地区征收的地方总额税。此外,地方政府面临的本地区资源约束式(7)变为:
(52)
相应地,代表性消费者面临的个人预算约束式(2)变为:
(53)
这样,代表性消费的问题是在预算约束式(53)的约束下,通过选择个人消费路径,以最大化个人一生效用式(1)。求解一阶条件,易得:
将式(55)代入式(1),得到消费者的间接跨期效用函数:
(56)
这样,地方政府的问题就是在预算约束式(51)和本地资源约束式(52)的约束下,通过选择地方公共支出及相应总额税,最大化消费者间接效用式(56)。通过求解一阶条件,我们可以得到地方政府的最优公共支出—产出比例(作为中央转移支付率的函数):
相应地,地方政府总额税为:
zs=βy.
(58)
进一步,我们将式(57)代入生产函数式(3),并利用g=g-i,得到
(59)
再将式(59)代入式(54),得到:
(60)
上式给出了作为中央转移支付率函数的均衡增长率。
(61)
将式(61)代入式(57),易得:
(62)
进一步,利用式(50)和式(57),可以得到中央政府总额税为:
zf=γy
(63)
再将式(61)代入式(59)和式(57),我们得到:
最后,我们将式(58),式(63)和式(64)代入消费函数式(55),得到:
(66)
通过比较均衡配置式(64)~(66)及其增长率式(60)与第一优配置式(46)~(48)及其增长率式(49),可知只要中央政府按式(61)设置最优转移支付率,地方政府按式(57)设置最优地方公共支出,且中央和地方政府均以总额税筹资,则分散均衡能够完美复制第一优配置。
命题4
在以总额税筹资的两级政府框架里,地方政府的最优地方公共支出(以公共支出与产出的比例衡量)函数为
中央政府的最优转移支付率为
相应地,地方政府最优公共支出(以公共支出与产出的比例衡量)为
地方和中央政府的最优总额税分别为zs=βy和zf=γy。如果中央和地方政府分别执行上述最优财政政策,则分散化决策经济能够实现社会第一优配置。
将命题4与正文部分的命题2和命题3进行比较,我们发现,无论在第一优配置还是次优配置中,地方政府的最优公共支出与产出的比例均为β+γ,说明这一最优比例具有税收中性的特征,即与政府部门采取总额税筹资还是收入税筹资是不相关的。与此同时,在第一优转移支付率与次优转移支付率之间存在一个税收楔子,说明收入税带来的扭曲对最优转移支付率产生了影响。
需要指出,虽然在总额税筹资模式下,分散经济可以实现社会第一优配置,但总额税在政策实践中的可行性相当低,从而分散经济通常只能实现次优配置的结果。我们对第一优配置以及总额税筹资模式的讨论,主要是为了提供一个参照系,使得我们能够清晰地认识到次优配置相对社会第一优配置,差异究竟在哪里。
附录2 不等式(26)的证明
证明:令Δ(φ)=(σ-α)φ+ρ,Λ(φ)=ρ-φ(1-σ)。为保证效用不发散,参数设定必然保证Λ(φ)>0,则Δ(φ)=Λ(φ)+(1-α)φ>Λ(φ)>0。
根据社会福利函数W(φ)的表达式式(25),我们求W对φ的导数,得到:
利用Δ=Λ+(1-α)φ>Λ>0,σ>0和0<α<1,我们得到:
证毕。
附录3υ*是φ(υ)全局唯一最大值解的证明
证明:根据φ(υ)的表达式式(28),我们首先求φ对υ的一阶导数,得到:
根据上式,我们进一步求φ对υ的二阶导数,得到:
以下,我们分两种情形考虑。
情形1:γ≤0
这时,在υ∈(-1,1)的定义域上,φ″(υ)<0,即φ(υ)严格凹。因此,一阶必要条件也是充分条件。υ*=γ/(γ+αβ)作为唯一满足一阶条件的解,必然是唯一的全局最大值解。
情形2:γ>0
由于φ(υ)在定义域υ∈(-1,1)上是连续函数,我们根据φ(υ)的一阶导数,得到如下分段结果:
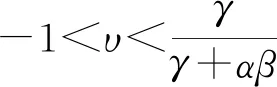
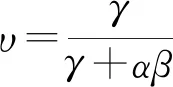

综合以上两种情形,υ*=γ/(γ+αβ)必然是全局唯一的最大值解。证毕。
附录4 不等式(41)的证明
证明:首先,根据式(39)和式(40),并利用β=1-α-γ消去β,我们得到:
进一步,我们将上式对参数γ求偏导,得到:
当γ>0时,必然有:
证毕。
