并行分批排序综述
2020-10-23井彩霞吴瑞强贾兆红
井彩霞,吴瑞强,贾兆红
(1.天津工业大学 经济与管理学院,天津 300387; 2.天津曙光存储科技有限公司 存储产品研发部,天津 300384; 3.安徽大学 计算机科学与技术学院,安徽 合肥 230601)
0 引言
并行分批排序来源于半导体芯片的加工和成品检验过程。在半导体芯片加工的扩散区有批加工设备高温扩散炉,在成品检验的预烧区有批加工设备预烧炉。批加工是指一台设备可同时加工多个工件,即批量加工。高温扩散炉和预烧炉除了批加工外,还有一个共同点就是用时都比较长。与其他工序用时几分钟、最多4个小时相比,高温扩散炉一般需要6~24小时,预烧作业一般要120小时左右。加工耗时长的特点,使其成为瓶颈机器。另外,批加工与非批加工方式的共存还会导致半导体生产线上加工流的不平稳。因此,对批加工设备进行优化调度具有重要的现实意义。除了半导体生产线,批加工的特点还出现在冶金、电镀等生产过程。日常生活中所用的烤箱也是一种批加工设备,可以同时烘烤一批面包,或面包和蛋糕一起烤。
以批加工为特点建立的排序模型即为广义的分批排序(batch scheduling)。对分批排序,国内外已有许多文献研究,所研究问题的种类也多种多样。分批排序按批加工的方式可以分为两大类:并行分批排序(parallel batch scheduling)和串行分批排序(serial batch scheduling)[1]。在并行分批排序中,同一批的工件同时加工,加工时间为批中所有工件的最大工时;在串行分批排序中,同一批的工件连续加工,加工时间为批中所有工件的工时之和。也有文献称这两种分批方式下的排序为平行分批排序和继列分批排序[2],或批处理机排序和成组分批排序[3]等。对并行分批排序也有文献称之为同时加工排序或批加工机器排序[4,5]等。
在早期的一些英文文献中,称分批排序为“scheduling with batching and lot-sizing”[6]、“batch scheduling”[7],“scheduling on batch processing machine”[8],或“scheduling on burn-in oven”[9]等,在名字上并没有对并行分批和串行分批做明显区分。然而近期的很多文献都用“parallel batch scheduling”[10,11]和“serial batch scheduling”[12,13]加以区别。随着理论的成熟,问题的分类更加细化,术语也越来越专业和科学化,这是科学研究发展的一个趋势。
考虑到所描述问题的机制和使用习惯,本文中采用 “并行分批”和“串行分批”来表示。本文主要对并行分批排序进行综述,且如无特别说明,所涉及的问题均为离线问题。
一般认为,Ikura和Gimple[14]是第一篇关于并行分批排序的文献,在工件加工时间相等且到达时间与交付期一致(agreeable)的情况下,其针对是否存在可行排序的问题,指出存在可行排序,并设计了一个时间复杂性为O(n2)的算法找出具有最小完工时间的可行排序。随后90年代比较有影响力的相关文献分别为Lee等[15]和Brucker等[16]。其中Lee等[15]较详细的阐述了并行分批排序产生的背景和研究的意义,并给出并行分批排序在单机和平行机环境下一些基本情形的解法。Brucker等[16]分别对批容量无限和批容量有限两种情况下的单台机器并行分批排序展开研究,在所有工件具有相同到达时间的假设下,分析了问题在多种目标函数下的复杂性,并给出相应算法。到了21世纪,关于并行分批排序问题的文献如雨后春笋般涌现,这种态势至今有增无减,其中的成果大多来自国内的科研工作者们。
关于并行分批排序问题的综述性文献主要有Webster和Baker[17]、 Brucker等[16]、Potts和Kovalyov[18]、 Baptiste[19]、张玉忠[20]、Mathirajan和Sivakumar[21]、张玉忠和曹志刚[1]等。本文在前人工作的基础上,对近10年来的研究成果和动态进行了综述和分析,同时为了综述的完整性,收录了部分已有综述文献的内容。
对已有成果涉及的并行分批排序问题进行梳理和分类如图1所示。本文将以问题为导向,按图1中的框架结构对并行分批排序进行综述。
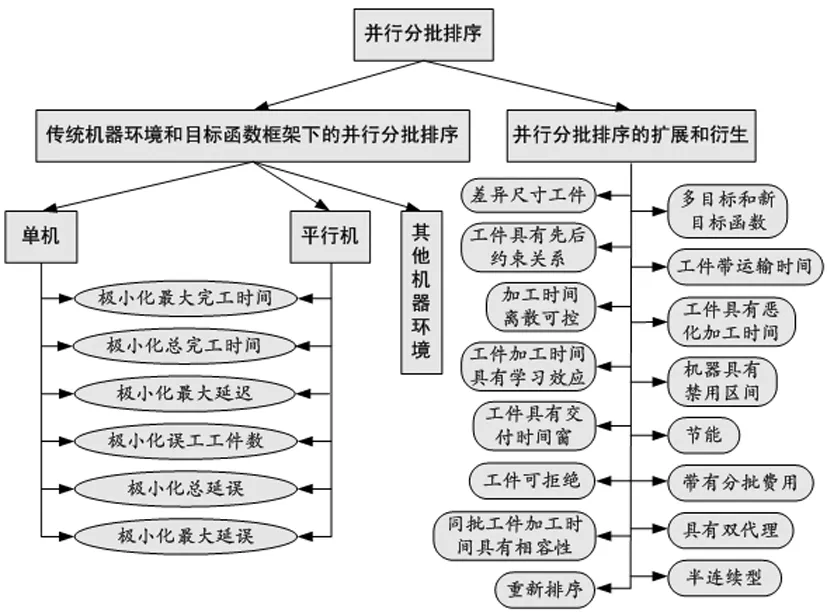
图1 已有成果中涉及的并行分批排序问题分类示意图
1 传统机器环境和目标函数框架下的并行分批排序
本节根据已有文献中的成果,主要对单机和平行机机器环境下的并行分批排序问题进行综述,在每种机器环境下,主要针对六个传统目标函数下的问题进行梳理,分别为极小化最大完工时间、极小化总完工时间、极小化最大延迟、极小化误工工件数、极小化总延误和极小化最大延误。
1.1 单机并行分批排序
单机并行分批排序问题的一般描述为:有n个工件J1,J2,…,Jn要在单台机器上加工,记工件Jj的加工时间为pj,到达时间为rj,交货期为dj,j=1,2,…,n。工件可成批加工,批容量为B,即机器每次最多可同时加工B个工件。同一批中的所有工件同时开始加工,并同时结束,加工时间为批中所有工件的最大加工时间。一旦某批工件开始加工,就不可中断,加工期间也不能增加或减少工件,直至该批加工完成。以极小化最大完工时间的目标函数为例,该问题可用三参数法表示为1|B,rj|Cmax。如果所有工件的到达时间都相等,则可表示为1|B|Cmax。
1.1.1 极小化最大完工时间的单机并行分批排序
在极小化最大完工时间的目标函数下,单机并行分批排序问题又可根据批容量是否有限、工件是否同时到达等特点分为很多类,下面主要根据这两个特点进行分类介绍。
(1)批容量无限
批容量无限是指B≥n,也记作B=∞。这时所有的工件都可放在一批加工。
①工件同时到达
显然,对排序问题1|B=∞|Cmax,只需把所有工件放在一批加工即得最优排序。
②工件不同时到达
对排序问题1|B=∞,rj|Cmax,Brucker等[16]设计了一个动态规划最优算法,说明该问题是多项式时间可解的,并给出一个定理。
定理1若记工件不同时到达、目标函数为Cmax的排序问题为P1,相应的工件同时到达、目标函数为Lmax的排序问题为P2,则P1和P2可以O(n)时间内相互转换。
Lee[22]也设计了一个动态规划算法,时间复杂性为O(n2)。Poon和Zhang[23]给出了一个时间复杂性为O(nlogn)的算法,并猜测这是理论上可能的最好算法。Yuan等[24]指出具有不相容工件簇(incompatible families)的排序问题1|B=∞,rj|Cmax是强NP-难的,这里“不相容工件簇”是指所有工件分成若干类、不同类的工件不能同批加工,有些文献中也称之为“不相容工件族”或“不相容工件组”。对该NP-难问题,Yuan等[24]给出两个时间复杂性分别为O(n(n/m+1)m)和O(mkk+1P2k-1)的动态规划算法,其中n为工件数,m为工件簇数,k为工件到达时间的个数,P为所有工件簇的加工时间和;另外,还给出一个紧界为2的启发式算法和一个多项式时间近似方案(polynomial time approximation scheme, PTAS)。
(2)批容量有限
批容量有限是指B ①工件同时到达 ②工件不同时到达 对排序问题1|B,rj|Cmax,其复杂性可由定理1和Brucker等[16]给出的另一个定理(定理2)推出。 定理2对具有交付期的批容量有限的单机并行分批排序,判断问题是否存在可行排序是强NP-难的,即使批容量B=2。 由定理2可知,排序问题1|B|Lmax、1|B|fmax、1|B|ΣUj、1|B|ΣwjUj、1|B|Tj和1|B|ΣwjTj都是强NP-难的。再由定理1可知,排序问题1|B,rj|Cmax也是强NP-难的。 此外,针对问题的一般情况,Deng等[27]给出了一个PTAS;孙锦萍等[28]给出了一个比Deng等[27]中时间复杂性更低的PTAS;Sung和Choung[9]给出分支定界算法和启发式算法;Li等[29]在排序问题1|B,rj|Cmax的基础上,考虑工件具有不同尺寸的特点,给出一个最坏性能比为2+ε的近似算法,并指出该算法在解工件具有相同尺寸的问题时,会成为一个近似方案(approximation scheme),并且时间复杂性低于Deng等[27]中的算法;李曙光等[30]给出一个总运行时间为O(nlogn+Cn)的PTAS,其中C仅与精度ε有关,改进了Deng等[27]中的PTAS。 Poon和Zhang[23]对到达时间个数确定和输入为整数的情况,设计了一个算法,时间复杂性为O(n(BRmax)m-1(2/m)m-3),其中m为到达时间的个数,Rmax为最后一个工件与第一个工件到达时间之差;并对到达时间个数和加工时间个数都确定的情况设计了一个算法,时间复杂性为O(nlogm+kk+2Bk+1m2logm),其中k为加工时间的个数。姜冠成[31]针对排序问题1|B,rj|Cmax建立0-1整数规划模型,并利用软件进行数值求解,得出能够获得最优解的问题规模。 另外,对排序问题1|B,rj|Cmax,井彩霞等[5]研究了工件成批到达的情况,该问题与工件到达时间个数为常数的问题是等价的。当只有两批工件时,Lee[22]给出了一个优势性质。基于Lee[22]的优势性质和FBLPT算法,井彩霞等[5]分别给出针对只有两批工件情况和一般情况的启发式算法。 1.1.2 极小化总完工时间的单机并行分批排序 对目标函数为极小化总完工时间的单机并行分批排序问题,本节同样也根据批容量是否有限和工件是否同时到达这两个特点分类介绍。 (1)批容量无限 ①工件同时到达 对排序问题1|B=∞|ΣwjCj,Brucker等[16]指出该问题是多项式时间可解的,并分别给出一个动态规划算法和一个逆向动态规划算法,时间复杂性分别为O(nlogn)和O(n2)。曹国梅[32]考虑具有不相容工件簇的排序问题1|B=∞|ΣwjCj,并给出多项式时间最优算法。 ②工件不同时到达 对排序问题1|B=∞,rj|ΣwjCj,Deng等[33]首先指出目标函数Σwj(Cj-rj)/Σwj、Σwj(Cj-rj)和ΣwjCj是等价的;然后证明了该问题是NP-难的;随后给出问题在工件加工时间的取值个数为常数时的多项式时间最优算法;并为排序问题1|B=∞,rj|ΣCj设计了一个PTAS。Li等[34]为排序问题1|B=∞,rj|ΣwjCj设计了一个PTAS,随后Liu和Cheng[35]设计了一个完全多项式时间近似方案(fully polynomial time approximation scheme,FPTAS)。曹国梅[32]考虑具有不相容工件簇的排序问题1|B=∞,rj∈{r1,r2,…,rk}|ΣwjCj,并给出一个启发式算法,时间复杂性为O(2k-1nlogn)。Liu和Cheng[36]指出排序问题1|B=∞,rj|ΣCj在多重性编码(id-encoding)下是NP-难的。 (2)批容量有限 ①工件同时到达 对排序问题1|B|ΣCj,Chandru等[37]给出了一个分支定界算法和两个启发式算法。Brucker等[16]给出了一个动态规划算法,时间复杂性为O(nB(B-1)),这说明当B为常数时,问题是多项式时间可解的。当B为变量时,Poon和Yu[38]对充分大的B,设计了时间复杂性为O(n6B)的算法。Cai等[39]设计了一个PTAS。 Chandru等[40]考虑工件具有多重性(high multiplicity)的分批排序问题1|B|ΣCj,给出一个动态规划算法,时间复杂性为O(r3Br+1),其中r为工件类型数。Hochbaum和Landy[41]将该时间复杂性改进为O(r23r),并针对工件类型数r不确定的情况,设计了一个2-近似算法。 对排序问题1|B|ΣwjCj,Uzsoy和Yang[42]以及Azizoglu和Webster[43]均给出分支定界算法;Liu和Tang[44]给出了分支定界算法和启发式算法;张召生和刘家壮[45]建立该问题的数学规划模型,并利用对偶理论证明了SPT序是B=1情况下的最优解。苗翠霞和张玉忠[46]对所有工件加工时间都相等的特殊情况,给出最优算法。张玲玲等[47]给出问题在两种特殊情况下的多项式时间最优算法:一种情况是工件到达时间为正整数和具有单位加工时间;另一种情况是工件到达时间个数为常数和加工时间相等。 ②工件不同时到达 排序问题1|B,rj|ΣCj是强NP-难的[48,49]。丁际环等[50]证明了排序问题1|B,rj∈{0,r}|ΣCj是NP完备的,并设计了一个最坏性能比为2的近似算法。对排序问题1|B,rj|ΣCj,Chang等[51]利用约束规划给出分支定界算法。Deng等[52]针对批容量B为常数的情况,给出PTAS。Liu和Cheng[35]针对B为变量的情况,给出PTAS。 Baptiste[19]对排序问题1|B,pj=p,rj|ΣwjCj给出了一个多项式时间的最优算法。任建锋和张玉忠[53]对排序问题1|B,rj|ΣwjCj给出一个PTAS。苗翠霞和张玉忠[54]证明了排序问题1|B,rj∈{0,r}|ΣwjCj是NP完备的。 1.1.3 极小化最大延迟的单机并行分批排序 当目标函数为极小化最大延迟时,根据批容量是否有限和工件是否同时到达这两个特点分类介绍如下。 (1)批容量无限 ①工件同时到达 对排序问题1|B=∞|Lmax,Brucker等[16]给出一个逆向动态规划算法,时间复杂性为O(n2),这说明该问题是多项式时间可解的。 ②工件不同时到达 对排序问题1|B=∞,rj|Lmax,Cheng等[55]证明了该问题是NP-难的,并针对几种特殊情况给出多项式时间算法。 (2)批容量有限 ①工件同时到达 由定理2可知,批容量有限、工件同时到达的排序问题1|B|Lmax是强NP-难的。Uzsoy[56]研究了具有不相容工件簇的情况,并给出多项式时间最优算法。李文华和王炳顺[57]讨论了问题存在只分一批为最优解的充分条件。Cabo等[58]设计邻域搜索方法对排序问题1|B|Lmax进行求解。 ②工件不同时到达 显然,排序问题1|B,rj|Lmax也是强NP-难的。Wang和Uzsoy[59]首先给出一个动态规划算法,判断给定序列的所有工件是否都可在交付期前完工;针对不能按期完工的情况设计了一个启发式算法来极小化最大延迟;然后以启发式算法为适应度函数设计了一个遗传算法;最后又将遗传算法和二分搜索(bisection search)相结合,给出了二分搜索遗传算法。Zhang和Ma[60]对排序问题1|B,rj|Lmax给出了一个PTAS。Uzsoy[56]研究了具有不相容工件簇的情况,并设计了启发式算法。 1.1.4 极小化误工工件数的单机并行分批排序 在极小化误工工件数的目标函数下,根据批容量是否有限和工件是否同时到达这两个特点分类介绍如下。 (1)批容量无限 ①工件同时到达 ②工件不同时到达 Liu等[61]对排序问题1|B=∞,rj|Σfj给出了伪多项式时间的动态规划算法,其中fj=fj(Cj),为工件Jj完工时间Cj的非减函数,可以为ΣUj,ΣwjUj,ΣTj,ΣwjTj,ΣCj或ΣwjCj等。 (2)批容量有限 ①工件同时到达 当批容量有限,且工件同时到达时,由定理2可知,排序问题1|B|ΣUj和1|B|ΣwjUj都是强NP-难的。Jolai[62]考虑具有不相容工件簇的排序问题1|B|ΣUj,并指出当工件簇数和批容量任意时,问题是NP-难的,并给出了一个动态规划算法。Li和Chen[63]研究工件分组,同组工件交付期相同的排序问题1|B|ΣwjUj,给出了一个伪多项式时间算法和一个FPTAS,并分别考虑了权重相等和加工时间相等的情况,并给出多项式时间最优算法。王春香和王曦峰[64]对交付期相等的排序问题1|B,dj=d|ΣUj,设计了一个时间复杂性为O(n3logn)的最优算法。刘丽丽等[65]对相同问题给出时间复杂性为O(nlogn)的最优算法。 ②工件不同时到达 当工件具有到达时间时,Lee等[15]指出排序问题1|B,rj|ΣUj是NP-难的,并考虑了工件到达时间和交付期一致情况下的排序问题1|B,pj=p,rj|ΣUj,给出一个动态规划算法,时间复杂性为O(n2B)。Li和Lee[66]指出工件到达时间和交付期一致的排序问题1|B,rj|ΣUj是强NP-难的,并研究了工件到达时间、交付期和加工时间都一致的情况。Baptiste[19]指出排序问题1|B,pj=p,rj|ΣwjUj是多项式时间可解的。 1.1.5 极小化总延误的单机并行分批排序 对极小化总延误的单机并行分批排序问题,根据批容量是否有限和工件是否同时到达这两个特点分类介绍如下。 (1)批容量无限 ①工件同时到达 ②工件不同时到达 Liu等[61]对排序问题1|B=∞,rj|Σfj给出了伪多项式时间的动态规划算法,其中fj=fj(Cj),为工件Jj完工时间Cj的非减函数,可以为ΣTj,ΣwjTj,ΣUj,ΣwjUj,ΣCj或ΣwjCj等。 (2)批容量有限 ①工件同时到达 当批容量有限,工件同时到达时,由定理2可知,排序问题1|B|ΣTj和1|B|ΣwjTj都是强NP-难的。Mehta和Uzsoy[68]考虑具有不相容工件簇的排序问题1|B|ΣTj,指出当工件簇数和批容量为任意数时该问题是强NP-难的,并给出动态规划算法和启发式算法。刘丽丽等[65]对交付期相等的排序问题1|B,dj=d|ΣTj给出伪多项式时间最优算法,时间复杂性为O(B2dnB2-B+2)。 ②工件不同时到达 同样由定理2可知,排序问题1|B,rj|ΣTj是强NP-难的。Baptiste[19]指出排序问题1|B,pj=p,rj|ΣTj是多项式时间可解的。 1.1.6 极小化最大延误的单机并行分批排序 当目标函数为极小化最大延误时,由排序问题1|rj|Tmax是强NP-难的,可知排序问题1|B,rj|Tmax也是NP-难的。Ikura 和 Gimple[14]研究了工件到达时间与交付期一致的情况。Lee等[15]给出优于Ikura和Gimple[14]中算法的动态规划算法,并研究了加工时间和交付期一致,以及所有工件加工时间相等的情况。Li 和Lee[66]指出工件到达时间和交付期一致的排序问题1|B,rj|Tmax是强NP-难的,并研究了工件到达时间、交付期和加工时间都一致的情况。Baptiste[19]指出排序问题1|B,pj=p,rj|Tmax是多项式时间可解的。 在平行机环境下,并行分批排序问题一般可描述为:有n个工件J1,J2,…,Jn要在m台平行机上加工,记工件Jj的到达时间为rj,交付期为dj,在机器Mi上的加工时间为pij,j=1,2,…,n,i=1,2,…,m。工件在每台机器上都可成批加工,批容量为B,即机器每次最多可同时加工B个工件。同一批中的所有工件同时开始加工,并同时结束,加工时间为批中所有工件的最大加工时间。一旦某批工件开始加工,就不可中断,加工期间也不能增加或减少工件,直至该批加工完成。以同型平行机和极小化最大完工时间的目标函数为例,该问题可用三参数法表示为P|B,rj|Cmax。如果所有工件的到达时间都相等,则可表示为P|B|Cmax。下面本节根据目标函数的不同对平行机并行分批排序问题进行分类介绍。 (1)极小化最大完工时间 在极小化最大完工时间的目标函数下,Lee等[15]指出并行分批排序问题P|B|Cmax是强NP-难的,并给出最坏性能比为4/3-1/3m的算法,其中m为机器数。张玉忠等[69]利用转换引理对排序问题P|B|Cmax给出最坏性能比为2-1/m的算法,并指出该界是紧的,同时对排序问题Q|B|Cmax给出了近似算法。刘丽丽和张峰[70]为排序问题Pm|B=∞,rj|Cmax设计了一个伪多项式时间的动态规划算法和一个FPTAS。Li[10]研究了平行多功能机环境下加工集合具有嵌套结构的并行分批排序问题PMPM|B,rj|Cmax,给出一个近似比为4-1/m的快速算法和一个PTAS,并对工件具有相同到达时间的特殊情况给出一个近似比为3-1/m的快速算法。 (2)极小化总完工时间 在极小化总完工时间的目标函数下,Chandru等[37]对排序问题P|B|ΣCj,给出两个启发式算法。任建锋和张玉忠[53]对排序问题Pm|B,rj|ΣCj给出批容量B和机器数m为常数情况下的PTAS。Li等[71]对排序问题P|B=∞,rj|ΣwjCj给出一个PTAS。李曙光等[72]对排序问题P|B,rj|ΣCj也给出了一个PTAS。苗翠霞和张玉忠[54]证明了排序问题P2|B|ΣwjCj是NP-完备的。 (3)极小化最大延迟 在极小化最大延迟的目标函数下,Lee等[15]指出并行分批排序问题P|B|Lmax是强NP-难的,并给出了一个列表算法满足不等式 其中L为列表算法所得的目标函数值,L*为问题的最优目标函数值,dmax表示最大交付期。另外Lee等[15]还指出即使在交付期相同、且交付期和加工时间一致的情况下,排序问题P|B|Lmax也是强NP-难的。张玉忠等[69]对排序问题Q|B|Lmax给出了近似算法。Li等[77]对排序问题P|B,rj|Lmax给出一个PTAS。Liu等[78]指出所有具有到达时间和交付期的批容量无限的平行机并行分批排序问题都是NP-难的,即使到达时间和交付期是一致的,且m=2;另外还对排序问题Pm|B=∞,rj|Lmax设计了一个PTAS。 (4)极小化误工工件数 在极小化误工工件数的目标函数下,刘丽丽和张峰[79]为排序问题Pm|B=∞|ΣUj设计了伪多项式时间的顺向动态规划算法。 (5)极小化总延误 在极小化总延误的目标函数下,Mönch等[80]考虑具有不相容工件簇的排序问题Pm|B,rj|ΣwjTj,并给出启发式算法。Mönch 和Almeder[81]对具有不相容工件簇的排序问题Pm|B|ΣwjTj,提出了一个蚂蚁系统(ant system,AS),与已有的基于调度规则的方法和遗传算法相比,可以获得稍好的解质量,且运算时间大大减少;另外,与最大最小蚂蚁系统(max-min ant system)比较,两者所得解的质量相当,但最大最小蚂蚁系统需要更多的运算时间。Bilyk等[82]考虑了具有不相容工件簇且同簇工件具有相同加工时间的排序问题Pm|B,rj,prec|ΣwjTj,并设计了启发式算法。 (6)极小化最大延误 在极小化最大延误的目标函数下,刘丽丽和张峰[79]为排序问题Pm|B=∞|Tmax设计了伪多项式时间的顺向动态规划算法。 除了单机和平行机,还有文献考虑其他机器环境下的并行分批排序问题,如流水作业[83]、柔性流水作业[84]、混合流水作业[85]和柔性异序作业(flexible job shop)[86]等。 前文主要以传统的机器环境和目标函数为框架,对并行分批排序问题进行了综述。随着科学研究的发展和进步,以及新的需求的产生,并行分批排序问题不断得到扩展和衍生,尤其近几年来,出现了很多新特点下的并行分批排序问题。 在前面介绍的并行分批排序问题中,默认工件具有相同的尺寸。随着相关领域设备与技术的不断发展和进步,以及用户需求的不断变化,加工任务也更加多样化,导致出现更加复杂的并行分批排序问题,其中工件或机器在尺寸或容量上出现差异性就是一个典型的新特点。下面将根据机器容量是否相同,对差异尺寸工件的并行分批排序问题进行分类介绍。 2.1.1 相同机器容量的差异尺寸工件并行分批排序 当机器容量相同时,已有文献中对差异尺寸工件并行分批排序问题的研究主要集中在极小化最大完工时间的目标函数。下面将分别对该目标函数下的单机环境和平行机环境问题进行综述。 (1)单机环境 Uzsoy[87]证明排序问题1|S,sj|Cmax是NP难的,并基于FF(first fit)规则,给出了几种启发式算法,仿真实验表明其中的FFLPT(batch first fit & longest processing time)算法性能较优。此外,Uzsoy[87]还给出了一个基于工件尺寸排序的启发式算法,即FFDECR(batch first fit & decreasing order of sizes)算法。Zhang等[88]证明了FFLPT算法的最坏性能比不超过2,FFDECR算法的最坏性能比可能任意大;提出了一个启发式算法,最坏性能比为7/4;同时还考虑了尺寸大于1/2的大工件的加工时间不少于尺寸小于1/2的小工件加工时间的情况,并设计了一个最坏性能比为3/2的启发式算法。Dupont和Dhaenens-flipo[89]对排序问题1|S,sj|Cmax提出了两个启发式算法,分别为BFLPT(best fit & longest processing time)算法和SKP(successive knapsack problem)算法,并证明了BFLPT算法是当时求解该问题的最优启发式算法。Kashan等[90]将Zhang等[88]中假设的工件尺寸1/2扩展为1/m,其中m≥2为整数,并给出了绝对性能比(absolute worst-case ratio)为3/2、渐进性能比(asymptotic worst-case ratio)为(m+1)/m的算法。 还有一些研究者致力于将智能算法应用于该问题的求解。Melouk等[91]首先引入模拟退火算法对问题1|S,sj|Cmax进行求解,实验结果表明该模拟退火算法所得解的质量优于商用软件CPLEX,并提出目前通用的一种基于随机方式生成仿真实验测试算例的方法。Kashan等[92]给出了两个不同思路的遗传算法,其中一个思路是先生成工件序列,然后再对工件进行分批;另一个是先生成批序列,然后再通过启发式的过程来保证解的可行性,最后通过合并和拆分来构建批序列。Damodaran等[93]也采用遗传算法求解了该问题,通过对工件序列进行编码,针对问题包含的加工序列和分批两个方面的约束,对遗传算法的交叉与变异算子进行了新的设计,实验结果表明该算法优于Melouk等[91]中的模拟退火算法。Cheng等[94]考虑了模糊制造系统下的单机并行分批排序,并提出一种结合Metropolis准则的改进型蚁群优化算法,其中Metropolis准则是一种随机选择机制,可以使算法以一定的概率接受差的解从而避免陷入局部最优。Chen等[95]从聚类的角度给出一个聚类算法,计算实验表明该算法优于BFLPT算法和Damodaran等[93]中的遗传算法。Jia和Leung[96]对排序问题1|S,sj|Cmax给出了一个下界,并提出一种改进的最大最小蚁群算法,计算实验表明,该算法优于Uzsoy[87]中的FFDECR算法和FFLPT算法、Kashan等[92]中的遗传算法,和Chen等[95]中的聚类算法等。 此外,对排序问题1|S,sj|Cmax,Cheng和Kovalyov[97]考虑了工件加工时间随着加工资源数量减少而减小、具有交付期和批带有准备时间的情况,提出了两种动态规划算法极小化最大完工时间。Dupont和Dhaenens-flipo[89]和Koh等[98]都考虑了工件具有不相容工件簇的情况,其中Dupont和Dhaenens-flipo[89]给出一个分支定界算法;Koh等[98]给出了一系列的启发式算法和遗传算法,并且除了极小化最大完工时间,还考虑了极小化总完工时间和极小化总加权完工时间的目标函数。程八一 等[99]研究了具有模糊批加工时间和模糊批间隔时间的情况,并提出一种集成粒子群优化和差异演化的混合算法。 对工件具有到达时间的差异尺寸工件单机并行分批排序问题1|S,sj,rj|Cmax,Sung和Choung[9]提出了性能较好的启发式算法;Li等[29]给出一个最坏性能比为2+ε的近似算法;Chou等[100]给出一个混合遗传算法;Xu等[101]给出混合整数规划模型和下界,并设计了一个启发式算法和一个蚁群优化算法,计算实验表明,所提蚁群优化算法比Chou等[100]中的混合遗传算法具有更好的性能;吴翠连[102]针对尺寸大于1/2的大工件的加工时间不少于尺寸小于1/2的小工件加工时间的情况,给出最坏性能比为3/2+ε的近似算法;张玉忠等[103]考虑只有两个到达时间且工件加工时间和尺寸大小一致的情况,并给出最坏性能比不超过33/14的算法;马冉和张玉忠[104]研究了具有特殊到达时间、工件加工时间相等且具有优先约束的情况,给出最坏性能比不超过2的近似算法。 (2)平行机环境 相对于差异尺寸工件的单机并行分批排序问题,平行机并行分批排序问题的求解难度更大。当问题因约束复杂而求解难度增大时,研究者往往采用智能算法对问题进行求解。 针对差异尺寸工件的平行机并行分批排序问题Pm|S,sj|Cmax,Chang等[105]提出了模拟退火算法,并通过仿真实验验证所提模拟退火算法的求解性能优于商业软件CPLEX。Damodaran和Chang[106]提出了若干启发式算法,他们将问题分解为工件分批和批分配至机器两个子问题,分别采用了FFLPT算法和BFLPT算法分批,再利用LPT和Multifit启发式规则对批进行排序,其中Multifit规则本质上是一种二分法,其通过判断问题目标值上下界的平均值是否可行来不断减小上界或增大下界,从而逐渐缩小上下界的距离,获得问题的近似解。实验结果表明Damodaran和Chang[106]所提启发式算法在大规模问题上的性能优于CPLEX,与Chang等[105]中的模拟退火算法相当。Shao等[107]将神经网络应用于该问题,通过与Damodaran和Chang[106]中所提的启发式算法进行对比,验证了神经网络方法的优越性。Kashan等[108]提出一种混合遗传启发式算法,该算法通过遗传算子产生随机批来搜索解空间。在该算法中,对每一个生成的后代染色体,采用一个随机分批过程用于保证其可行性;然后通过LPT规则将生成的可行批排序到机器上;最后通过两个局部搜索启发式算法进一步改进算法的求解效果。实验结果表明混合遗传启发式算法优于Chang等[105]提出的模拟退火算法。Damodaran等[109]设计遗传算法来求解排序问题Pm|S,sj|Cmax,仿真实验结果表明,所提遗传算法的性能优于模拟退火算法、随机键遗传算法和混合遗传启发式算法。杜冰等[110]论证了平行机并行分批排序问题Pm|S,sj|Cmax实质为一种广义聚类问题,并基于批的空间浪费比,提出批的约束凝聚聚类算法,为分批排序问题的求解提供了一种新的途径。Jia和Leung[111]基于最大最小蚂蚁系统算法和Multifit规则提出一种智能算法ASM(Ant system based meta-heuristic)求解排序问题Pm|S,sj|Cmax,计算实验表明,ASM算法的性能优于Damodaran和Chang[106]中的启发式算法和Kashan等[108]所提的混合遗传启发式算法。 另外,对排序问题Pm|S,sj|Cmax,张鑫等[112]研究了工件可以按尺寸拆分的情况,指出该问题是NP-完备的,并给出一个最坏性能比不超过11/4-1/m的近似算法;Chen等[113]针对工件具有到达时间的情况,分别设计了蚁群优化算法和遗传算法;吴翠连和陈俊[114]考虑工件具有到达时间、且尺寸大于1/2的大工件的加工时间不少于尺寸小于1/2的小工件加工时间的情况,并设计了一个最坏性能比为3/2+ε的多项式时间近似算法;Zhou等[115]针对工件具有到达时间的情况,设计了几个启发式算法,计算实验表明,这些算法在解的质量上优于已有的几个启发式算法和智能算法。 Li等[116]研究了非同类机排序问题Rm|S,sj|Cmax,给出了一个下界,并基于BFLPT算法设计了几个启发式算法。Arroyo和Leung[117]考虑工件具有到达时间的排序问题Rm|S,sj,rj|Cmax,给出混合整数规划模型和下界,并设计了几个有效的启发式算法。 2.1.2 不同机器容量的差异尺寸工件并行分批排序 当排序问题Pm|S,sj|Cmax中机器容量由相同扩展到不同时,就得到机器容量不同且差异尺寸工件的平行机并行分批排序问题,用三参数法可表示为Pm|S,sj|Cmax,其中Si表示第i台机器Mi的容量。 已有研究中,对不同机器容量的并行分批排序问题涉及的较少。对排序问题Pm|Si,sj|Cmax,Damodaran等[118]给出了一个粒子群优化算法;Jia等[119]设计了两个启发式算法,并通过计算实验表明其性能优于Damodaran等[118]中的粒子群优化算法。贾兆红等[120]基于工件松弛的方法给出了一个下界的计算方法,并设计了一个启发式算法H和一个蚁群优化算法,计算实验表明,所提蚁群优化算法性能优于启发式算法H和Damodaran等[118]中的粒子群优化算法。Zhou等[121]研究了同类机排序问题Qm|Si,sj|Cmax,给出混合整数规划模型,并设计了基于差分进化算法的混合算法,计算实验表明该算法在解的质量和鲁棒性方面优于CPLEX商业软件、随机键遗传算法和粒子群优化算法。 在排序问题Pm|Si,sj|Cmax中,若工件具有到达时间,就成为排序问题Pm|Si,sj,rj|Cmax。Xu和Bean[122]构建了排序问题Pm|Si,sj,rj|Cmax的整数规划模型,提出基于随机键的遗传算法。Chen等[113]指出排序问题Pm|Si,sj,rj|Cmax是强NP难的,分别基于FBLPT算法和机器负载给出了问题的两个下界,并分别设计蚁群优化算法和遗传算法对工件分批问题进行求解,再采用ERT-LPT(earliest release time-longest processing time)启发式规则将批分配到平行批处理机上。Wang和Chou[123]首先分别用模拟退火算法和遗传算法将工件分配到机器上,然后采用多阶段动态规划算法对每台机器上的工件进行分批。Jia等[124]基于松弛的方法提出了一个下界,并设计了一个启发式算法和一个蚁群算法,计算实验表明,所提蚁群算法优于Wang 和Chou[123]中的遗传算法和Damodaran等[118]中的粒子群优化算法。 另外,对排序问题Pm|Si,sj,rj|Cmax,Li[125]针对不同批容量数固定的情况,给出近似比任意接近2的算法;Li[126]针对具有包含关系结构的多功能机环境,设计了一个PTAS。Arroyo和Leung[127]研究了非同类机排序问题Rm|Si,sj,rj|Cmax,给出了下界和混合整数规划模型,并设计了基于迭代贪婪算法的智能算法。 除了单目标函数,还有文献研究双目标或多目标函数下的并行分批排序问题,如张召生等[128]、李文华[129,130]、He等[131]、焦峰亮等[132,133]、Liu等[134]、李小衬[135]、Geng和Yuan[136,137]、Zhang等[138]等。除了常见的目标函数,张玉忠和王琳[139]研究目标函数为加权延迟工作和的排序问题1|B=∞|ΣwjVj,其中Vj=min{Tj,pj};李文华[130]讨论了目标函数为极小化完工时间平方之和的单机并行分批排序问题。 Cheng等[140]研究了工件具有先后约束且加工时间相等的单机并行分批排序问题。邹娟和张玉忠[141]、马冉等[142]、卜宪敏等[143]和刘伟[144]考虑了具有平行链约束的单机并行分批排序问题。 柏孟卓和唐国春[151]、王磊和张玉忠[152]研究加工时间离散可控的单机并行分批排序问题。这里加工时间离散可控是指工件具有若干可选的加工时间,每个备选加工时间都对应一个控制费用,一般要使工件在比较短的时间内完工,需要付出比较大的费用,加工时间和费用因素均在目标函数的考虑之中。 在并行分批排序问题中,工件具有恶化加工时间(deteriorating job)是指工件的实际加工时间与开始时间有关,开始加工时间越晚,需要的加工时间越长,一般这种关系用线性函数来表示。在Qi等[153]、Miao等[154]、Li等[155]、Zou和Miao[156]所研究的模型中,工件Jj的实际加工时间为pj=bjt,其中t为开始加工时间,bj为恶化率;余英等[157]考虑了恶化加工时间为pj=p(a+bt)的单机并行分批排序问题,其中p为基本加工时间,a,b为正的常数,t为开始加工时间;在Miao等[158]中,恶化加工时间计算公式为pj=αj(A+Dt),其中αj为恶化率,A,D为正的常数,t为开始加工时间。 Yuan等[161]和齐祥来等[162]考虑机器具有禁用区间(forbidden interval)的单机并行分批排序问题,这里机器具有禁用区间是指机器在给定的禁用时间区间内不能加工工件,一般出于机器需要定期维护的考虑。 Zhao和Li[163]、韩国勇等[164]和赵洪銮等[165]研究工件具有交付时间窗(due window)的单机并行分批排序问题。交付时间窗由交付期扩展而来,通常给定交付期为某个时间点,而交付时间窗为某个时间区间,若工件在该时间区间内完工,则是按期完工;如果完工时间早于区间开始时间或晚于区间结束时间,则是提前或延迟完工,会产生惩罚费用。显然,交付时间窗可给予工件完工时间更大的灵活性。如果给定工件交付期,完工时间早于或晚于交付期都会受到惩罚,则为准时(just-in-time)排序问题,李文华等[166]研究了准时单机分批排序问题。 在生产调度中考虑能源效率即得节能排序问题。已有考虑节能并行分批排序的文献多数都是针对单机环境的。在单机环境下:Mouzon和Yildirim[167]研究同时极小化总能耗和总延迟时间的问题;Yildirim和Mouzon[168]考虑了同时极小化总完工时间和能源消耗的问题,并给出了一个多目标的遗传算法;Shrouf等[169]建立了一个极小化能源消耗成本的数学规划模型;Liu等[170]考虑了到达时间确定的双目标并行分批排序,优化的目标为总完工时间和总二氧化碳排放量;Che等[171]研究了极小化总电力成本的并行分批排序问题,并给出启发式算法; Cheng等[172]研究了实时电价下的并行分批排序问题,同时极小化最大完工时间和总的电力成本,给出混合整数规划模型并证明该问题是NP难的;Wang等[173]考虑实时电价下、具有不同的能源消耗功率,且工件有不同尺寸的双目标问题,目标函数为极小化最大完工时间和总能源成本。 在平行机环境下,Moon等[174]研究了同时极小化最大完工时间和电力成本的非同类机并行分批排序问题,并提出一种混合的遗传算法;Jia等[175]研究了同时极小化最大完工时间和电力成本的同型机并行分批排序问题,并给出一个基于Pareto优化的蚁群优化算法。在混合流水作业环境下,Luo等[176]研究同时极小化最大完工时间和电力成本的并行分批排序问题,并提出一种基于蚁群的智能算法。 在实际加工过程中,制造商往往会因为资源有限的原因拒绝加工部分订单,而选择加工那些来自其重要客户或能够带来更多利润的订单。将这类实际问题抽象出来即为工件可拒绝的排序问题。工件可拒绝是指在加工过程中,可以拒绝加工某些工件,但需要支付一定的拒绝费用。王珍等[177]、Cao和Yang[178]、Lu等[179]、翟大伟[180]、李修倩等[181]、Zou和Miao[156]、He等[182]研究工件可拒绝的单机并行分批排序问题。Jia等[183]研究了极小化最大完工时间和被拒绝工件成本总和的双目标排序问题Pm|pj=p,sj,ωj,S|Cmax+Rtot和Pm|pj=p,sj,ωj,S|(Cmax,Rtot),其中ωj表示被拒绝工件Jj的拒绝成本,Rtot表示被拒绝工件的成本总和。 张喆和冯琪[184]、张喆等[185]、张喆和李文华[186,187]考虑带有分批费用的单机并行分批排序问题,这里的分批费用是指每分一批就会产生一个固定费用,一般出于对实际生产中可能产生的人工费用或包装费用的考虑。 Bellanger等[188]和Li等[189]考虑同批工件加工时间具有相容性(job processing time compatibility)的单机并行分批排序问题。在该类问题中,工件Jj的实际加工时间取值范围为[aj,(1+α)aj],其中aj为基本加工时间,α>0为某个给定的数;同批工件必须具有相容性,即所有工件的实际加工时间取值范围相交非空;同批工件具有相同的开始加工时间,该时间由批中所有工件加工时间范围交集的左端点确定,即p(B)=max{aj:Jj∈B}。 Feng等[190]和Tang等[191]研究具有双代理的单机并行分批排序问题。在双代理问题中,有两个代理A和B,各自都有自己的工件集合和目标函数,但都在同一台批处理机器上进行分批加工;如果代理A和代理B相容,则不同代理的工件可同批加工,否则不能同批加工。 郭晓[192]和Xu等[193]研究了单机并行分批排序的重新排序(rescheduling)问题。重新排序是指原始工件集按目标函数分批排好顺序后,又有新的工件集到来,决策者需要将新工件集中的工件插入到已排好的顺序中,插入的原则为在不过分打扰原工件集中工件顺序的条件下,使新的目标值最优。这里不过分打扰可以具体为限制序列错位量和时间错位量等。 另外,还有一种分批排序问题,既有并行分批的特征又有串行分批的特点,但又不同于这两种形式,称为半连续型(semi-continuous)或连续型分批排序问题。在该类问题中,所有工件可任意分成若干批;分批后,批中所有工件的加工时间就都变为同批中所有工件的最大加工时间;在批加工的过程中,同批中的工件依次匀速进入和离开机器,每个工件都有自己的开始加工时间和完工时间;机器可同时容纳的最大工件数称为机器容量,这里需要说明一下,因工件依次匀速进入和离开,所以有可能存在同一批中有的工件已经完工了,但还有工件没进入机器的情况,所以批中工件数可以大于机器的容量;任一批中所有工件都完工后才可进行下一批的加工。Tang和Zhao[194]分别研究了极小化最大完工时间和极小化总完工时间的单机半连续型分批排序问题,给出最优性质和动态规划算法;赵玉芳[195]考虑了平行链约束情况下,目标函数为极小化最大完工时间的单机半连续型分批排序问题;吕绪华等[196]研究极小化加权总完工时间目标函数下的单机半连续型分批排序问题;王松丽等[197]考虑了工件具有到达时间、目标函数为极小化最大完工时间的情况,并给出动态规划算法。 本文综述了并行分批排序的已有成果,主要分为两部分,第一部分主要介绍了两种机器环境和六个目标函数组合下的并行分批排序成果,其中两种机器环境分别为单机和平行机,六个目标函数分别为极小化最大完工时间、极小化总完工时间、极小化最大延迟、极小化误工工件数、极小化总延误和极小化最大延误;第二部分主要梳理了16类新型并行分批排序,这些新型排序由一般分批排序和新特点结合产生,16个新特点分别为差异尺寸工件、多目标和新目标函数、工件具有先后约束关系、工件带运输时间、加工时间离散可控、工件具有恶化加工时间、工件加工时间具有学习效应、机器具有禁用区间、工件具有交付时间窗、节能、工件可拒绝、带有分批费用、同批工件加工时间具有相容性、具有双代理、重新排序和半连续型等。 虽然到目前为止,对并行分批排序的研究已经取得了丰硕的成果,但还是存在很多有待解决和研究的问题。如有些问题的复杂性还没有解决,有些问题的已有算法还可以改进等。另外,本文归纳出的16类新型并行分批排序都具有较强的应用背景,对这些问题进行深入研究具有重要的理论意义和现实意义。 除了上述对已有问题的深入和扩展,还可根据实际应用背景结合新的特点,如在半导体生产中最典型的重入特点、在制品库存目标和加工流平稳目标等。另外,目前已有的成果绝大部分停留在理论研究阶段,如何将理论研究成果转化为切实可用的实践方法是一项具有重大意义的挑战。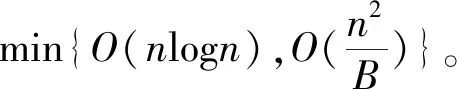
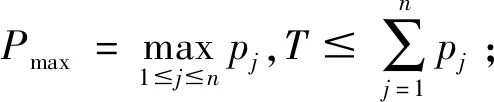
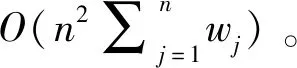
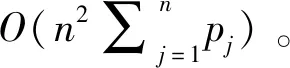
1.2 平行机并行分批排序
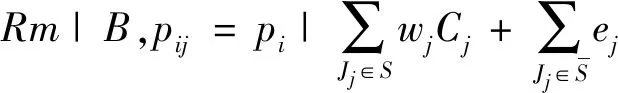
1.3 其他机器环境的并行分批排序
2 并行分批排序的扩展和衍生
2.1 差异尺寸工件的并行分批排序
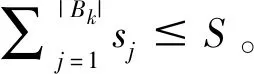
2.2 多目标和新目标函数下的并行分批排序
2.3 工件具有先后约束关系的并行分批排序
2.4 工件带运输时间的并行分批排序

2.5 加工时间离散可控的并行分批排序
2.6 工件具有恶化加工时间的并行分批排序
2.7 工件加工时间具有学习效应的并行分批排序
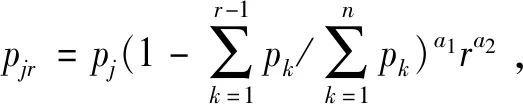
2.8 机器具有禁用区间的并行分批排序
2.9 工件具有交付时间窗的并行分批排序
2.10 节能并行分批排序
2.11 工件可拒绝的并行分批排序
2.12 带有分批费用的并行分批排序
2.13 同批工件加工时间具有相容性的并行分批排序
2.14 具有双代理的并行分批排序
2.15 并行分批排序的重新排序问题
2.16 半连续型并行分批排序
3 结语和展望
