我国股市网络稳定性及其宏观影响因素——基于三种网络拓扑结构、鲁棒性的实证研究

张伟平，庄新田，吴冬梅

(东北大学 商管理学院，辽宁 沈阳 110169)

0 引言及文献综述

复杂网络方法在金融市场中的应用日趋广泛，由于股票市场中的股票数量庞大、价格波动关联密切、网络结构复杂等特征[1]，学者们将网络理论用于金融市场的建模和分析[2,3]。在经济全球化背景下，股票市场的稳定对经济发展至关重要，金融市场关联日趋复杂，机构投资者之间互相持股关系紧密，外界任何不利因素的冲击都会导致股市系统性风险的不断累积，当风险累积到某个上限时会对金融体系的稳定性造成破坏。宏观经济波动会直接影响到企业的外部交易环境进而对股市稳定性产生冲击，因此股票市场的稳定性与股市网络自身结构特征和宏观经济状况密不可分[4,5]。

股票价格波动关联是某一特定时期股票市场运行的基本规律，股市中少数股票的价格波动，会引起其他多数股票甚至市场范围内的股价波动[6,7]，因此，基于股票价格波动关联便成为构建股市网络的最常用方法。Chi等[8]构建了美国股票价格关联网络，结果表明雅虎、谷歌等少数公司的股价波动，会引发整个股票市场指数的大幅波动。Alkan等[9]利用滑动时间窗口分析股票网络的演化规律，发现在某些特定时间前后股票价格波动关联程度存在显著差别。Birch等[10]构建以德国DAX30指数成份股为研究样本的股票关联网络，结果表明在经济危机时期的股票价格波动关联变化明显弱于经济复苏时期，并且利用股票网络结构特点预测宏观经济周期阶段。黄玮强等[11]构建动态演化的中国股票网络，发现随着时间推移，股票间价格波动关联关系越来越强，同行业的股票间易产生价格波动关联。以上研究可以很好的把握股票间的价格波动关联关系及股市结构的拓扑变化。进一步地，许多研究发现，金融资产价格不仅具有价格波动关联性，还普遍具有分形特征，即在不同的时间标度下价格波动具有相似性。已有研究表明金融市场中资产价格变动或收益率序列呈现出多重分形的特征[12,13]，Onali[14]利用分形理论探究了欧洲八个股票市场的有效性；Shan等[15]使用众多局部标度指标刻画实际序列中包含的更细致结构，这就要求在建立股市复杂网络时要考虑价格波动的多重分形性。袁铭[16]针对时间序列具有的多重分形特征，提出基于标度曲线测度沪深300成分股之间的相似性并实现了聚类。张鼎等[17]首次将分形理论和复杂网络理论进行结合，从时间和空间两个角度对中国股票网络的分形特征进行分析。袁铭[18]基于不同阶数下的标度曲线构造沪深网络，研究其网络拓扑性质并分析股票间的多重分形相似性。股票市场是一个高风险市场，股票价格的大幅波动，如2008年和2015年的股灾都是股价在某时点突然崩盘[19]，在短时间内给投资者造成了巨大损失，反映了股票价格波动系数不能够准确的刻画股价间的长期均衡关系，因此有学者开始以VaR模型为基础构建复杂网络模型，因为VaR模型提供了衡量市场风险的有效方法，并且VaR数组的相关系数反映了股票间风险上的相关性[20]，这为研究股票网络的系统性风险、风险传染和网络稳定性等提供了一个新的视角。

股市的稳定与宏观经济发展密切相关，宏观经济波动对实体企业、金融机构等经济部门都会产生影响，波动风险很容易通过金融网络进行传递并放大。Gray等[21]认为宏观经济波动对企业的负债和资产带来冲击效应，风险不断积累最终形成对金融体系的破坏力；李鳞等[22]认为宏观经济波动对银行业系统性风险的破坏是通过对银行不良资产比率的影响。随着金融经济的一体化程度不断提高，关联性随之加大，有学者开始对金融市场网络的稳定性[23]、鲁棒性[24]、脆弱性[25]等深层特征进行探究，Acemoglu等[26]认为尽管完全市场结构网络比环状结构网络更为稳健，但在极端情况下网络关联性越高金融体系的脆弱性也越高；黄聪和贾彦东[27]认为基于金融网络结构的系统性风险分析是推进我国宏观审慎监管政策的关键；Muller等[28]则认为忽略网络结构的系统性风险是不够准确的。逐渐地，有学者开始关注特定风险或事件对金融网络的影响，进而判断网络中的脆弱节点和重要节点，建立针对特定风险的应对策略[29]；张超等[30]依据风险事件发生规律和股票价格变化机制，实例分析各阶段应对策略对股票价格关联网络恢复力的影响。

综上分析，发现已有文献研究股票网络时多采用股票价格波动关联的建模方法，但该方法不能从长期上反映股价间的波动关系，忽略了时间序列的相似性特征。此外，绝大多数研究均单方面分析宏观经济对金融市场稳定性影响或网络结构对金融市场稳定性的影响，而将宏观经济变量和网络结构结合分析对金融稳定性影响的文献并不多。本文贡献体现在：同时考虑股票价格时间序列的相似性特征和股票市场的高风险特点，基于多标度曲线拟合法和VaR风险价值法，构建新的股票关联风险网络模型，探讨股市风险波动下三种网络结构的小世界性和无标度特性，对比了三种网络的鲁棒性、稳定性系数和波动率等股票市场稳定性特征。采用Johansen协整检验分析宏观经济变量和网络稳定性的长期均衡关系，发现在宏观经济变量的影响下，风险网络的鲁棒性最优，为衡量沪深股市的波动风险及制定系统风险防御策略提供了参考。最后是本文的结论。

1 关联网络的构建和网络稳定性指标

1.1 股票关联网络的构造方法

(1)基于股票价格的关联网络

目前构造股票关联网络最常用的方法是基于股票间价格波动的相关性，该方法通过股价计算收益率序列的Pearson相关系数，将相关系数转换成相应的度量距离，通过阈值法得到邻接矩阵，研究股票指标关联性[31,32]。在股票市场中有N支股票，在股票价格波动的关联网络中，网络节点表示单只股票，节点间的连边表示在时间T范围内股票价格波动的相关性，主要步骤如下：

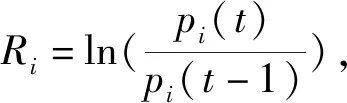
(1)

其中：<·>表示数学期望；ρi,j∈[-1,1]。因为Pearson相关系数ρi,j不满足度量空间(metric space)的三个条件，故将ρi,j转换为相应的度量距离dij，公式为：

(2)

由股票间的相关系数ρi,j可得相关系数矩阵C，由式(2)得到距离矩阵D，股票间的相关系数越小，它们间的度量距离相对越远。因为距离矩阵D为全连接矩阵，为了剔除冗余的边，一般采用平面最大过滤图法、最小生成树法和阈值法。

(2)基于多标度曲线的关联网络

基于股票价格序列的分形特征，即不同时间标度下股票价格波动具有相似性，并且这种相似性在不同阶数下也具有不同的特征。拟合不同阶数下标度曲线，利用曲线间的相关系数通过阈值法构造多标度网络。

1)基于MSDFA的标度曲线拟合

MSDFA是基于多标度退趋势波动分析(Multi-Scale Detrended Fluctuation Analysis, MSDFA)。Kantelhardt[33]提出验证一个非平稳时间序列是否具有多标度性的有效方法“MF-DFA”，参考文献[34]的做法，对MF-DFA进行拓展，主要步骤如下：

步骤1对于给定长度为N的时间序列{xi}(i=1,2,…,N)，构造如式(3)的新序列{yi}。

(3)

步骤2将{yi}分割成长度为s的等长度区间，共Ns=int(N/s)个。因为时间序列的长度N除以s后不一定是整数，为了不舍弃末尾数据，可逆向从序列尾部重复这一分割过程，因此得2Ns个区间。

步骤3应用OLS最小二乘法拟合每一个子区间v(v=1,2,…,2Ns)上的局部趋势项pv(j),j=1,2,…,s对子区间内的数据进行退势，得到残差序列。分成两种情况(首至尾序列和尾至首序列)：

当v=1,2,…,Ns时，

(4)

当v=Ns+1,Ns+2,…,2Ns时，

(5)

步骤4计算退趋势后2Ns个子区间的残差平方均值，即:

(6)

在此基础上给定阶数q构造波动函数Fq(s):

(7)

步骤5由式(8)计算局部广义Hurst指数h(sk):

(8)

步骤6由式(8)得到的h(sk)和sk的关系是离散的，可以使用三次样条插值法使其变为光滑标度曲线，从而能更加近似地分析h(sk)随着间隔距离s变化的规律。

2)多标度网络的构建

通过不同阶数标度曲线的拟合，即可构建基于序列的多重分形特征相似性的多标度曲线网络，参考文献[18]的描述，主要步骤如下：

步骤1对于金融时间序列i(i=1,2,…,N)，给定阶数qi,(i=1,2,…,L)，采用基于MSDFA的标度曲线拟合得到不同阶数的标度曲线hil(sk)，共L条标度曲线，每条曲线有K个观测值。该组标度曲线可构成一个K行L列的矩阵，将矩阵的每一列堆叠起来，可以转化成为一个KL行1列的向量Vi。

步骤2对任意一对金融时间序列i和j计算其相应向量Vi和Vj的相关系数ρij，注意因不同阶数下的标度曲线测度的i和j的多重分形相似性的贡献度不同，故应对不同阶数下的标度指数序列赋予权重wz，公式如下：

(9)

其中pij大于阈值θ时认为金融时间序列i和j之间有连边，即可认为邻接矩阵A中的元素aij=1，反之认为i和j之间无连边，则aij=0。

(3)基于风险价值VaR的风险网络

Jorion[35]给出风险价值VaR的权威定义为“给定置信水平下，某一资产或投资组合在未来持有期内的最坏的预期损失”,VaR能预测资产组合的潜在风险。运用VaR模型构造复杂网络，是利用VaR能预测资产组合的潜在风险的特点，计算VaR数组的相关系数，并用阈值法构造风险网络。

(10)

其中：“·”表示数学期望；Ci,j∈[-1,1]。判断所给定的阈值θ与Ci,j的大小，若θ小于或等于Ci,j，则节点对i和j之间有无向无权的边相连，反之没有边相连。

受宏观经济、金融市场及投资者自身特征的影响，各金融市场之间股票价格的波动存在一定的相互关联，基于此建立股市价格波动关联网络分析各个股票价格波动关联的动态规律；但注意到股票价格的变化不是随机游走的，而是具有增强趋势的持久性，即未来的股票价格变动与初始状态间并非相互独立，而是持续相关的，它描述股市中股票价格在相距较远的时间间隔具有显著的相似性。这说明仅建立股票价格关联网络不能准确反映股票市场各股票走势特点，需进一步考虑股票价格的分形特征建立多标度的股市网络。当然，股票市场的健康发展受金融风险传染的影响，故将金融风险纳入股市网络结构显得尤为重要，本文利用股票风险价值(VaR)之间的相关系数作为边，代表两只股票之间有风险传染关系，对股票中短期风险进行模拟。综合考率股票价格波动、股票价格相似性、股票间风险传染等股票走势指标构建股市网络，全面分析股市稳定性特征及影响因素。

1.2 网络稳定性指标

股票市场的稳定性受许多因素的影响，这些因素即有“外在因素”也有“内在因素”，前者主要指宏观经济波动等外部因素；后者主要指股票市场自身的因素，如投资者情绪、市场运行态势和网络结构等。本文使用股票市场网络的鲁棒性、稳定系数和波动率来测度股票市场的稳定情况，前两个指标是从股票网络的网络拓扑结构出发，后一个指标侧重股市的波动情况。

(1)网络崩溃程度指标

鲁棒性即网络结构对外界破坏的抵抗能力，鲁棒性较差的网络在运行中受到干扰或破坏时，性能会大大降低甚至功能完全丧失，鲁棒性较好的网络具有较强的健壮性，鲁棒性越强网络稳健性越强。用网络崩溃程度指标G反映网络的鲁棒性，即：

(11)

式中N为目标网络中所有节点的数量，N′为网络受到随机攻击或外界确定性攻击后得到的最大连通子图的节点数。当G=1时，网络是完整的；当G≤0.1时，定义网络被完全摧毁。

(2)稳定系数

用网络结构稳定系数衡量股票市场网络的稳定性。在2.1网络建模的基础上，参考Heiberger[36]的做法，定义稳定系数NS公式如下：

(12)

式中N为网络中节点数，D为网络的连接密度，S为网络节点的平均相互作用强度。NS<1表示网络为稳定网络，该值越大网络就越不稳定[36,37]。

(3)波动率

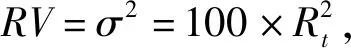
2 实证分析及结果

2.1 样本数据

选取沪深300指数成分股的日收盘价，研究期间为2006- 01- 04至2017- 06-30(共2792个交易日)，最终筛选出的股票应满足：在该研究期间内始终处于上市状态；样本股票连续停牌的时间不超过60天。最终得到符合条件的样本股83只。数据来自Wind数据库。

2.2 网络拓扑结构分析

基于多标度曲线方法构建网络时，首先根据日收盘价计算日对数收益率，然后利用MSDFA分析股票的多重分形特征，在计算过程中，时间标度S的最小值设为9，最大值设为N/5(N为总的交易天数)，每9个单位取一个S值；阶数q的取值范围设定为[-10,10]；用于退势的多项式阶数为1。基于在险价值方法构建网络时，时间跨度选100个交易日。使用2.1节给出的三种构建股票关联网络的方法，阈值作为控制边存在的参数变量，即选用阈值法作为构建邻接矩阵的方法。

股票价格相关系数的均值为0.4，多标度曲线相关系数的均值为0.4及风险价值相关系数的均值为0.6，故构建价格网络、多标度曲线网络和风险网络选择的阈值分别等于0.4、0.4和0.6。用Ucinet和Pajek软件，画出的三个关联网络拓扑结构如图1。

(a)Stock price network

(b)Multiscale curve network

(c)Risk network图1 基于股票价格、多标度曲线和风险价值的沪深股市网络

注：节点标记大小代表节点的介数中心性。

节点的介数反映了节点或边在整个网络中的作用力和影响力，它是全局特征量。某节点可能起到连接两个社团的作用，如果该节点受到攻击，那么就可能导致两个社团的联系中断，严重威胁到网络的稳定性。从图1(b)中清晰的看到，介数中心性最大的节点数为1个，所以相比于其他两个网络，在受到外界影响下网络结构最先受到破坏，表现出强烈的不稳定性；而(a)和(c)中介数中心性较高的节点比较多，网络结构更为复杂。

为更全面了解并比较三种网络的拓扑结构特征及其复杂性，下面给出各种设定下网络的统计特征如表1。其中标度指数λ是由节点度分布的双对数图(ln(P(k*)～lnk*))得到。

表1 三种网络统计特征描述

从表1看出，多标度曲线网络和风险网络的标度指数值分别为2.43和2.40(均介于2～3之间)，表明多标度曲线网络和风险网络都具有无标度特征，而价格网络的标度指数为1.67(不在2～3之间)，说明价格网络不具有无标度特性。三种网络的聚集系数看都远大于0，说明三个网络都具有小世界性。此外，发现风险网络的平均路径长度最小，说明风险网络具有最强的稳定性。因为在网络的信息传递过程中，节点之间信息一般以某条最短路径进行传输，经过路径越少，可靠性越强，网络鲁棒性也越强。因此进一步挖掘风险网络并对风险网络稳定性深入分析是非常有价值的一个环节。

2.3 网络鲁棒性

下面主要研究网络的静态鲁棒性，以此来反映网络的稳健性特点。网络的静态鲁棒性是只删除网络中的某些节点时，网络中不发生流量的重新分配，但是网络依然可以保持它的正常功能的能力。通常用网络崩溃程度指标来衡量网络的鲁棒性。本文给出了股价关联网络、多标度曲线网络和风险网络的鲁棒性分析，比较得出哪种网络更稳健。

目前的研究中，把网络的攻击大致分为2类：一类是对网络的节点或边进行完全随机移除，称为随机攻击(Random)；二类是对网络中度值较大或介数较大的节点进行移除，称为蓄意攻击(Infected)。分析结果如图2(图2中圆圈连线表示随机攻击下p与G的关系、星号连线表示蓄意攻击下p与G的关系)。

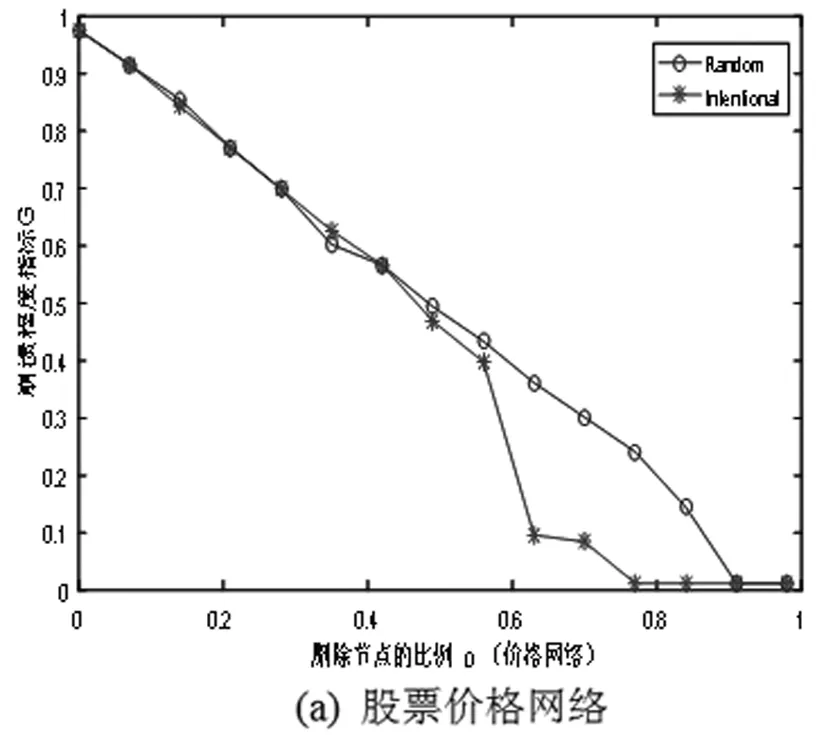
(a)Stock price network

(b)Multiscale curve network

(c)Risk network图2 两种攻击下不同网络的p与G的关系

从图2看出，对网络的随机攻击造成的破坏明显弱于网络的蓄意攻击。当网络遇到随机攻击时，多标度曲线网络在摧毁70%的节点时，网络就已经处于将近崩溃的状态，而对于价格网络和风险网络，只有当摧毁节点的比例达到90%以上时，网络崩溃程度指标才小于0.1，网络处于瘫痪状态。当网络遭遇蓄意攻击时，价格网络中的节点删除比例达到63%时，网络结构抵抗外界干扰的能力大大降低，网络接近崩溃；多标度曲线网络中，摧毁节点的比例为42%时，网络结构的抗攻击能力出现断崖式下跌，崩溃指标为0.2，网络性能大大降低，当摧毁63%的节点时，网络结构崩塌；风险价值网络中，攻击70%的节点时，才会使网络结构接近崩溃的状态。对比三种网络的抗随机攻击和蓄意攻击能力发现，风险网络无论是在随机攻击，还是在蓄意攻击情况下，都表现出较强的鲁棒性，网络结构更加稳健。从股市的影响因素看，国际金融市场环境、货币政策、宏观调控等都会对股市网络结构、股市价格波动产生影响，或是随意干扰或是蓄意干扰，因此，分析宏观经济因素对股票市场网络稳定性的影响显得尤为重要。

2.4 网络稳定性及其影响因素研究

2.4.1 稳定特征分析

从图3看出，沪深股票市场风险网络的稳定系数和波动率的变动趋势大致相同，都可以分为两大阶段：第一阶段从W1窗口到W25窗口(2006q1～2011q4)，第二阶段是W26窗口到W46窗口(2012q1～2017q2)。特别是在W11和W39窗口前后网络稳定系数都达到本阶段的最大值，网络稳定性最差，股市波动率也呈现出高强度的波动。这与实际相符，此时我国股市恰好处于2008年金融危机和2015年股市动荡时期。(a)图中稳定系数呈现出逐年波动上升的总趋势，2015年前后的稳定系数显著大于2008年前后，并且此时的股市波动率也达到最大值，说明近几年股市风险网络结构表现出更大的不稳定性，并且这种不稳定性与股市的异常波动存在一定的关系。下边对两者进行格兰杰因果关系检验，进一步确定这种关系。

图3 沪深股市稳定性指标的变动趋势

格兰杰因果关系检验的前提是时间序列是平稳的，故首先对NS和RV两个时间序列进行ADF单位根检验，单位根检验的结果表明：NS在1%的显著性水平下拒绝原假设，即NS是平稳序列；RV在10%的显著性水平下是平稳序列。检验结果如表2。

表2 稳定系数NS与波动率RV的格兰杰因果关系检验

由表2可知，拒绝原假设“NS不是RV的格兰杰原因”的概率为0.0043，故拒绝原假设，说明沪深股市风险网络的稳定性系数是股市波动的原因；同理，拒绝原假设“RV不是NS的格兰杰原因的概率为0.0002”，故拒绝原假设，说明沪深股市(收益率)波动是沪深股市网络结构稳定系数的原因，并且股市收益率波动的前期变化能有效解释股市网络稳定系数的变化。

2.4.2 网络稳定性与宏观经济变量间关系

股票市场风险网络的稳定性刻画了股票间风险传染的关联结构模式的稳定性，这里用稳定系数来衡量网络稳定性。为分析影响网络稳定系数的宏观经济因素，选取以下四个经济变量：GDP增长率可从宏观上反映经济周期的变化，股票市场的活跃程度随着经济周期繁荣衰退而变化；利率是资金的价格，从企业的角度它直接影响企业融资的成本，进而影响企业在股市中股价变化；CPI从消费者角度反应社会物价水平，该指标的高低直接影响着国家的宏观经济调控，进而间接影响股票市场；房地产近年来成为推动经济发展的重要产业，成为投资者关注的热点之一。

选取的变量有：GDP增长率(按累计季度同比增长率计算，记作GDPg)；利率R(按6个月短期贷款利率计算)；消费物价指数CPI(按当月同比增长率计算，将每一季度内各月份同比增长率取平均值作为该季度的CPI数据)；房地产价格(按商品房销售总金额与商品房销售总面积之比计算)，为消除房地产价格中的异方差影响，对房地产价格进行对数处理，记作lnEP。为与网络稳定系数指标数据保持一致，以上宏观经济变量分别按季度数据进行计算。

(1)长期均衡关系分析

首先检验被解释变量网络稳定系数NS及宏观经济解释变量GDP增长率、消费者物价指数CPI、利率R和房地产价格指数lnEP时间序列的平稳性。平稳性检验结果表明：NS在1%的显著性水平下服从零阶单整，GDP增长率、消费者物价指数CPI和利率R在1%的显著性水平下服从一阶单整过程，而房地产价格指数lnEP 服从二阶单整过程。严格意义上讲，进行协整检验的前提是同阶单整，但如果变量个数多于两个，当解释变量的单整阶数高于被解释变量的单整阶数时，则必须至少有两个解释变量的单整阶数高于被解释变量的单整阶数的情况下，也可使用协整检验[38]，运用Johansen协整检验的方法，检验稳定系数NS和GDP增长率、CPI和利率之间是否存在协整关系。结果如表3至表5。

表3 网络稳定系数NS与GDP增长率的协整关系检验

表4 网络稳定系数NS与消费者物价指数CPI的协整关系检验

表5 网络稳定系数NS与利率R的协整关系检验

从表3至表5看出，风险网络稳定系数NS与GDP增长率、消费者物价指数CPI和利率R等宏观经济变量间存在协整关系，并且至少存在一个协整关系。这说明沪深股票市场风险网络与这些宏观经济变量间存在长期的均衡关系。

(2)短期动态关系分析

由于样本数量的限制，在分析短期动态关系时，直接将网络稳定系数NS、GDP增长率、CPI和利率R划为一组来观察。并且在分析多变量间的协整关系基础上，通过建立向量误差修正模型(VECM)，观察变量间的短期动态关系。表6是风险网络稳定系数NS与宏观经济变量GDP增长率、CPI和利率R间的Johansen协整检验结果。从表6中可看出，在5%的显著性水平下，四者之间至少存在一个协整关系。

表6 网络稳定系数NS与GDP增长率、CPI、利率R的协整关系检验

在此基础上，建立向量误差修正模型如下：

ΔNSt=-0.0595(NSt-1-0.1700GDPgt-1+1.9286CPIt-1-0.4825Rt-1-4.7120)

+0.0605ΔNSt-1+0.1927ΔNSt-2-0.3463ΔGDPgt-1-0.1325ΔGDPgt-2

+0.2020ΔCPIt-1-0.0620ΔCPIt-2-0.2218ΔRt-1+0.7496ΔRt-2-0.0281

(13)

ΔGDPt=-0.1522(NSt-1-0.1700GDPgt-1+1.9286CPIt-1-0.4825Rt-1-4.7120)

-0.0869ΔNSt-1+0.0778ΔNSt-2-0.1043ΔGDPgt-1-0.1382ΔGDPgt-2

+0.1068ΔCPIt-1+0.0199ΔCPIt-2+1.1207ΔRt-1-1.2475ΔRt-2-0.1788

(14)

ΔCPIt=-0.2198(NSt-1-0.1700GDPgt-1+1.9286CPIt-1-0.4825Rt-1-4.7120)

+0.0187ΔNSt-1+0.2467ΔNSt-2-0.2205ΔGDPgt-1-0.1968ΔGDPgt-2

+0.3872ΔCPIt-1+0.2665ΔCPIt-2+2.6627ΔRt-1-0.8331ΔRt-2-0.0319

(15)

ΔRt=-0.0372(NSt-1-0.1700GDPgt-1+1.9286CPIt-1-0.4825Rt-1-4.7120)-

-0.0194ΔNSt-1-0.0781ΔNSt-2-0.0611ΔGDPgt-1-0.0751ΔGDPgt-2

+0.0682ΔCPIt-1+0.0807ΔCPIt-2+0.3819ΔRt-1-0.1972ΔRt-2-0.0374

(16)

在VECM模型的基础上，进行脉冲响应分析。因本文主要探究在宏观经济变量的影响下，风险网络稳定性变化情况，即把风险网络稳定性指标当作脉冲响应量，而把宏观经济变量看作VAR模型中的内生性变量，故此处仅给出脉冲响应变量稳定系数NS的脉冲响应函数，如图4所示。

图4 NS,GDPg,CPI,R的脉冲响应函数图

从图4看出，对当期GDP增长率进行正向冲击，对当期风险网络稳定系数NS立即产生负向的影响，这种负向影响在6个季度后达到最大值，随后略有减小并维持稳定的趋势。这说明GDP增长率的上涨，宏观经济环境的向好会刺激投资者投资于股票市场，促使股票价格上升，进而使网络稳定系数NS减小，即股票市场风险网络结构处于更加稳定的状态。消费者物价指数CPI当期的正向冲击在初始的3个季度内对风险网络稳定系数NS产生正向影响，并在第2季度正向效应达到顶峰，但在第3季度后冲击效应由正转负，并在第11季度的负向效应达到最大，随后这种负向效应稍有减小后趋于平稳。说明消费者物价指数CPI对风险网络稳定性的影响是复杂的，这是由于CPI的适当增长可促进经济发展，进而对股市运行是有利的，但过高的CPI说明通货膨胀压力较大，就会引发货币紧缩政策，影响资金供给及流动性，对股市是利空消息，故而网络稳定系数增大，网络结构稳定性降低，股市短期波动风险加剧；但当3个季度后，CPI指数在合适的范围内略有增加对股票市场是利好的，风险网络的稳定系数降低，即股票市场网络结构稳定性增强，这说明消费者物价指数CPI对风险网络稳定性的影响是“先抑后扬”的态势。利率的当前正向冲击在初始的2个季度内对网络稳定系数的影响是负向的，但这种负向效应并不显著，自第2季度后冲击效应由负转正，随着时滞的延长，这种正向效应逐渐增强，并在第6个季度达到最大后趋于稳定。这说明利率的上升，促使公司融资成本提高，公司预期收益下降，进而导致股价下跌，破坏股票市场的网络稳定性。需指出的是，利率对网络稳定系数产生促进作用的影响并非同期的，具有2个季度的滞后性。

3 结论

股市网络结构稳定性特征及影响因素的分析对于有效识别股市风险、风险预警及股票投资具有重要意义。本文从网络建模的视角出发，运用三种建模方法，选取我国沪深300指数成份股从2006年到2017年的数据，建立了股票价格网络、多标度曲线网络和风险网络。分析了股市网络包括鲁棒性、稳定系数和波动率在内的股票市场稳定性特征，并且运用Johansen协整检验和向量误差修正模型实证分析了宏观经济变量对鲁棒性最优的风险网络稳定性的影响。结论如下：

(1)基于股票价格、多标度曲线和风险价值构建的沪深股市网络，通过网络结构分析，发现三者都是典型的小世界网络，说明股票市场的股票间具有较小的平均路径，故股票间的风险也很容易通过股票关联网络传染给另外的股票。但是股票价格网络不具有无标度特征，多标度曲线网络和风险网络都具有无标度特征，说明在这两种网络具有“马太效应”，并且风险网络和多标度网络中存在较多的Hub节点，而这些节点所示的股票在风险传染和股票交易中都会对其他股票产生较大影响。

(2)从网络稳定性的鲁棒性角度看，对比三种网络的抗随机攻击和蓄意攻击能力，发现风险网络无论是在随机攻击还是在蓄意攻击情况下，都表现出较强的鲁棒性，进而使网络结构更加稳健。比较三种网络拓扑指标聚类系数，发现聚类系数最高的价格网络其鲁棒性最差，而聚类系数次之的风险网络鲁棒性最优，与Stefania等[39]认为的聚类系数越高的网络鲁棒性越好的观点相违背。这是由于风险网络的最短路径长度最小，而在网络的通信过程中，节点之间常以某条最短路径进行传输，经过路径最少，网络可靠性越强，网络越稳健。

(3)从网络稳定性特征角度分析股市波动率和股市稳定系数间的关系，对两者进行格兰杰因果关系检验，结果表明：沪深股市风险网络稳定系数是股市波动的原因，同时沪深股市波动是网络结构稳定系数的原因，并且股市收益率波动的前期变化能有效解释股市网络稳定系数的变化。

(4)考虑宏观经济变量的影响，发现风险网络稳定系数与宏观经济变量GDP增长率、消费者物价指数CPI和利率间存在较强的相关关系，两者具有长期的均衡关系。从短期来看，GDP增长率的提高，经济繁荣会抑制风险网络稳定系数的增大，促使股票风险网络结构趋于更加稳定。消费者物价指数CPI对网络稳定性的影响呈现“先抑后扬”的态势，应保持CPI在一个合理的范围以维护股票市场网络结构的稳定。利率的上升，会破坏股票风险网络的稳定性，并且利率对网络稳定性的破坏作用并非同期的，而是具有2个季度的滞后性。

综上，发现在宏观经济变量的影响下，风险网络的鲁棒性最优，为衡量沪深股市的波动风险及制定系统风险防御策略提供了参考。研究结果表明，近年来随着我国股票市场的不断发展，股市波动性也不断增大，整个股票市场也处于更大的不稳定状态。这些除了股票市场本身的网络结构等内因影响外，外部宏观经济变量的影响作用也不容忽视。维持国民经济平稳健康发展、降低利息率、保持消费者物价指数合理范围内增长和规范房地产价格，对于降低股市网络系统性风险，增强股市网络稳定性具有积极作用。