基于蒙特卡罗方法的中国中长期煤炭需求预测
2020-10-23侯小超
侯小超,张 磊,杨 晴
(1.中国矿业大学 管理学院,江苏 徐州 221116; 2.西安科技大学 管理学院,陕西 西安 710054)
0 引言
煤炭作为中国的主体能源,在一次能源结构中占比70%左右,是中国经济持续、快速发展的基本保障,其主体地位在未来相当长时期内不会改变。当前,中国经济发展进入新常态,经济由高速增长转为中高速增长,产业结构不断优化升级,能源结构步入战略性调整期,能源革命加快推进,由主要依靠化石能源供应转向由非化石能源满足需求增量,煤炭行业面临重大的挑战。对于煤炭行业来说,在目前的经济及能源结构转型期,只有正确预测未来煤炭的需求,才能更好地适应行业的转型,进而更好地支撑能源系统的转型。
当前的煤炭需求预测的研究方法大致可以分为两类。一类是基于煤炭需求序列进行分析预测[1~5],如时间序列法、灰色预测模型法等。宁云才应用复合小波神经网络模型对中国煤炭消费的年增长率进行了预测,得出该预测模型用于近期预测是可靠的[1]。池启水和刘晓雪以1953~2005年的煤炭消费历史数据建立ARIMA(3,1,3)模型,对2002~2005的煤炭需求进行预测,证明其预测误差较低,ARIMA 模型对于短期预测精度较高[2]。张会新和白嘉运用灰色系统和三角模型预测中国2008~2013年的煤炭需求量,研究结果显示灰色系统用于短中期预测较为准确,不适用于长期预测[3]。另一类是基于煤炭需求影响因素进行分析预测[6~11],如能源消费弹性系数法、部门分析法等。陈师等采用协整技术选用经济增长、城市化和工业化等作为煤炭需求影响因素,分高、中、低三种经济增长速度情景假设各影响因素的取值,对中国2012~2030年的煤炭需求进行预测[6]。高俊莲等基于LEAP模型选用GDP、人口和产业结构等作为影响煤炭需求的因素,分高、中、低三种煤炭发展前景,设定各影响因素取值,预测中国2015~2030年的煤炭需求[7]。刘畅和孙超将部门分析法、煤炭消费弹性系数法和GDP单位耗煤法三种方法组合,根据经济发展、产业结构、能源结构和生态环境的现状和政策,分别设定各种方法的影响因素的取值,预测中国2017~2020年的煤炭需求[8]。
以上煤炭需求预测可能存在的不足在于,基于煤炭需求序列的分析预测不适用于中长期预测,而基于煤炭需求影响因素进行分析预测的方法通常在参数取值上有一定的情景假设性。为此,本文尝试选取影响因素数据随机生成的蒙特卡罗方法,预测中国的中长期煤炭需求。该方法既能用于预测中长期的煤炭需求,又能规避参数取值的主观性问题,从而更为科学地回答中国煤炭需求预测问题。
1 研究方法
1.1 蒙特卡罗方法
蒙特卡罗方法(Monte Carlo Method, MC)也称统计模拟法或随机抽样技术,是20纪40年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法,其采用随机抽样来模拟事物的真实情况。当这种模拟次数足够时,模拟数据的概率分布特征就越接近实际情况[12]。蒙特卡罗方法的原理是当问题或对象本身具有概率特征时,可以用计算机模拟方法产生抽样结果,根据抽样计算统计量或者参数的值;随着模拟次数的增多,可以采用对各次统计量或参数的估计值求平均的方法得到稳定结论[13]。
蒙特卡罗方法的基本思想是,根据实际的工程或管理问题,以目标值建立一个概率模型g(x1,x2,…,xn) ;构造输入参数(x1,x2,…,xn)的概率分布,并从这些已知概率分布中抽样;根据概率模型g(x1,x2,…,xn)得到基于输入样本的随机目标值;用同样的方法产生N个随机目标值;最后,对N个随机目标值的概率分布进行拟合,这一概率分布即可被看作是目标值的概率分布,从而得到实际工程或管理问题的近似解。
蒙特卡罗方法的一般建模步骤[14,15]:
(1)建立输入参数和目标值的函数关系;
(2)构造输入参数的概率分布;
(3)基于已知输入参数概率分布的抽样;
(4)根据步骤(1)建立的函数关系得到随机目标值;
(5)重复步骤(3)和(4)N次,得到N个随机目标值;
(6)对N个随机目标值的概率分布进行拟合。
1.2 MC在预测领域的应用
蒙特卡罗方法用于预测的研究很多,涉及的领域也很广泛。曹玲运用基于独立同分布中心极限定理的蒙特卡罗方法对中国“十三五”期间经济增长率的概率分布进行预测,从预测结果来看,“十三五”期间中国经济增长速度将进入“新常态”,这与中国当前的经济状况相符[13]。陈俊松在对公路工程经济评价的概率分析中,运用蒙特卡罗方法对某新建公路未来20年的交通量做出预测,预测结果与给定的特征年限交通量相符合,预测结果良好[14]。徐廷学等将马尔可夫链与蒙特卡罗仿真相结合,根据某类备件季度消耗量序列来预测该类备件未来1年的需求量,为低需求量备件的预测提供借鉴[16]。杨金玲等将蒙特卡罗方法用于预测嫩江流域汛期降雨量,研究表明,该方法在汛期降雨量接近平水时,都会收到较好的预测精度,但在丰水和枯水的情况下,预测误差较大[17]。赵志鹏运用蒙特卡罗方法和队列要素人口预测算法对河南省2010~2050年的总人口数量、死亡人数和出生人数进行预测,将两种方法的预测结果进行对比,差值都在0.6%以内[18]。
蒙特卡罗方法在能源领域也有少量的应用。黄建基于LEAP模型选用电力消费的主要终端部门对中国中长期电力需求量进行预测,并运用蒙特卡罗方法对电力需求量预测结果进行不确定性评价,给出各年份电力需求量的概率分布图和基于95%置信区间,即各年份电力需求量的不确定性区间[15]。Henning Meschede等用蒙特卡罗方法评估海岛酒店可再生能源系统成本,考虑随机的天气、入住率和能源需求因素,分情景预测能源系统的成本[19]。然而,运用蒙特卡罗方法预测煤炭需求的文献尚未发现。
2 模型与MC仿真
2.1 回归模型的构建
作为基础能源,煤炭需求的影响因素众多,参考国内外的研究结果,我们选取三个主要影响因素,即经济增长、能源结构和产业结构。
(1)经济增长
众多学者的研究表明,中国经济增长是导致煤炭需求增长的主要原因。林伯强等采用协整技术研究中国长期煤炭需求,证明国民收入对煤炭需求有正向的影响[20]。高俊莲等基于LAEP模型,选用GDP等作为主要影响因素,对中国2015~2030年的煤炭需求进行预测[7]。本文选用GDP表示经济增长。为了真实反映GDP的变化,剔除通货膨胀因素的影响,以1980年不变价表示各年份的GDP。
(2)能源结构
中国的能源结构是以煤炭为主,煤炭在国民经济中占据着不可替代的主导地位。胡雪棉和赵国浩选取煤炭占总能源消费的比重等作为解释变量,基于BP神经网络构建煤炭需求预测模型,对中国2007~2011年的煤炭需求进行预测[21]。刘畅和孙超分析了能源结构等影响煤炭需求的因素,采用组合预测方法对中国2017~2020年的煤炭需求进行预测[8]。本文选用煤炭消费量占总能源消费量的比重作为衡量能源结构的指标。
(3)产业结构
现阶段中国正处于工业化发展进程中,工业生产对煤炭等能源具有巨大的直接需求。张宏和李仲学研究了产业结构等影响煤炭需求的因素,建立了煤炭需求情景分析模型,对中国中长期的煤炭需求进行了情景分析及预测[22]。陈师等选用工业化水平等作为影响因素,采用协整技术研究中国长期煤炭需求[6]。本文以工业增加值占GDP比重作为衡量产业结构的指标。
基于以上分析,构建如式(1)所示的煤炭需求模型:
lnQt=β0+β1lnGDPt+β2lnERSt+β3lnISt+εt
(1)
其中,Qt表示第t期的煤炭需求量;GDPt表示第t期的国内生产总值,即GDP;ERSt表示第t期的能源结构;ISt表示第t期的产业结构;εt表示第t期的随机扰动项。为消除异方差的影响,所有变量均用对数形式表示[6]。
2.2 参数的随机性分析
蒙特卡罗方法用于预测的文献中显示,影响因素的概率分布多为基于时间点构建,每个时间点一个概率分布,各时间点上的概率分布不一定相同[13~19,23,24]。为避免这一问题,同时为了降低影响因素概率分布构建的难度,本文选择基于影响因素的时间序列构建概率分布。这要求影响因素的时间序列整体上具有随机性,需要对序列整体的随机性进行检验。盛春光在中国碳金融市场发展机制研究中指出,非平稳时间序列在各个时间点上的随机规律是不同的,难以通过序列已知的信息去掌握时间序列整体上的随机性[25]。这给我们的研究转换了思路,将检验时间序列整体的随机性转为检验序列的平稳性。
常用的平稳性检验方法有ADF检验、PP检验和KPSS检验。为了更严谨地检验序列平稳性,本文同时采用这三种检验方法进行单位根检验,KPSS检验与ADF检验、PP检验的不同之处在于其原假设为时间序列是平稳的。检验结果如表1所示,lnGDP和lnERS序列非平稳,lnGDP和lnIS的变化率lnGDP_GR和lnIS_GR序列平稳,此处lnGDP_GRt=(lnGDPt-lnGDPt-1)/lnGDPt-1,lnERS_GR和lnIS_GR是由lnERS和lnIS采用同样的计算方法得到。lnIS序列的KPSS检验结果表明序列平稳,但ADF检验与PP检验结果表明序列非平稳,因此,lnIS序列非平稳。同理,lnERS_GR序列平稳。lnGDP,lnERS和lnIS序列非平稳,序列整体上不具有随机性,不可用于概率分布构建,而它们的变化率lnGDP_GR,lnERS_GR和lnIS_GR序列平稳,序列整体上具有随机性,可用于概率分布构建。

表1 单位根检验结果
2.3 蒙特卡罗仿真设计
根据蒙特卡罗模拟的一般步骤,将1980年作为第0期,1981年作为第1期,以此类推2025年为第45期,其中1980年的数据作为初始数据,而随机抽样从1981年开始。各影响因素对数变化率连续抽样45次,即根据已知分布生成45个随机数,前35个随机数对应1981~2015年的真实数据,不需要对参数的取值范围进行控制,后10个随机数对应2016~2025年的预测数据,需要控制参数的取值范围;根据生成的随机数、煤炭需求模型和第0期的数据计算出每期的煤炭需求对数lnQt,得到一个45期的煤炭需求对数时间序列;大量的实践经验表明,蒙特卡罗模拟次数取1000次已经能取得很好的估计值[14],因此,将此过程进行1000次,得到1000个45期的煤炭需求对数时间序列;最后将每期对应的1000个目标值进行平均得到每期的稳定目标值,再将稳定的目标值作为指数,自然常数e作为底数即可得到每期的煤炭需求。基于以上分析,本文的蒙特卡罗仿真设计如图1所示。
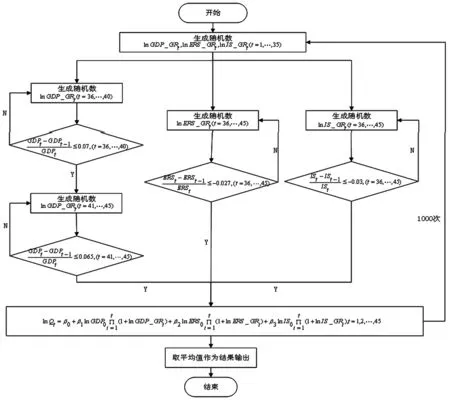
图1 MC模拟流程图
2.4 控制参数取值范围
当前,中国经济发展进入新常态,经济由高速增长转为中高速增长,产业结构不断优化升级,能源结构步入战略性调整期,能源革命加快推进,由主要依靠化石能源供应转向由非化石能源满足需求增量。针对这些现状,本文对影响煤炭需求的三个变量在预测期间的取值范围进行控制,同时为充分保证蒙特卡罗模拟时随机抽样的随机性,参数的取值范围仅设置上限或下限。
(1)经济增长。当前,中国经济发展进入新常态,经济由高速增长转为中高速增长。因此,预测期间的GDP年平均增长率应该会下降到某一平稳水平,为保证这一平稳水平,在进行蒙特卡罗模拟时应控制GDP取值范围。王少平和杨洋根据简约的协整VECM模型计算出GDP的长期趋势分布于5.5%~7.5%之间,GDP增速具有91.5%的概率稳定在6%~7.5%的区间[26]。因此,本文假设2016~2020年,GDP年增长率的上限为7%,2021~2025年的年增长率上限为6.5%。
(2)能源结构。中国能源结构步入战略性调整期,能源革命加快推进,由主要依靠化石能源供应转向由非化石能源满足需求增量。《煤炭工业发展“十三五”规划》称预计到2020年,煤炭消费比重下降到58%。因此,本文假设2016~2025年,煤炭消费占总能源消费比重年增长率上限为-2.7%。
(3)产业结构。由历史数据可知,2011~2015年工业增加值占GDP比重年平均下降率为3%。因此,本文假设2016~2025年工业增加值占GDP比重年平均增长率上限为-3%。
3 结果及讨论
3.1 模型系数估计
基于1980~2015年间的历史数据,利用MATLAB软件中的regress函数对煤炭需求模型的系数进行估计,得到结果如表2所示。回归方程的判定系数R2=0.9637,回归方程拟合程度较好;lnGDPt,lnERSt和lnISt与lnQt分别在1%和5%的显著性水平下线性关系显著;回归方程的线性回归效果在1%的显著性水平下显著,表明煤炭需求Qt显著受到GDPt、ERSt和ISt三个因素影响。煤炭需求模型的最终形式如式(2)所示:

表2 煤炭需求模型系数估计结果
lnQt=-3.7848+0.6161lnGDPt+
1.7202lnERSt-0.8943lnISt
(2)
3.2 概率分布拟合
我们收集了各影响因素1980~2015年的历史数据,构建其对数变化率的频率分布直方图,并基于直方图假设各影响因素对数变化率的概率分布,然后对该假设进行相关检验并得出结论,最后估算出各分布的均值和标准差。
(1)lnGDP变化率
从图2a来看,可以假设lnGDP_GR服从正态分布,故采用Lilliefors方法对其进行检验,其P值的结果为0.4691,表明可以接受原假设。基于最大似然估计法得到其均值为0.0094,标准差为0.0028,所以lnGDP变化率的概率分布为:lnGDP_GR~N(0.0094,0.00282)。
(2)lnERS变化率
从图2b来看,可以假设lnERS_GR服从正态分布,故采用Lilliefors方法对其进行检验,其P值的结果为0.2119,表明可以接受原假设。基于最大似然估计法得到其均值为0.0103,标准差为0.0441,所以lnERS变化率的概率分布为:lnERS_GR~N(0.0103,0.04412)。
(3)lnIS变化率
从图2c来看,可以假设lnIS_GR服从均匀分布,根据详细的频率分布直方图假设lnIS_GR服从-0.03到0.05间的均匀分布,故采用kstest函数对其进行检验,其P值的结果为0.4821,表示可以接受原假设,所以lnIS变化率的概率分布为:lnIS_GR~U[-0.03,0.05]。
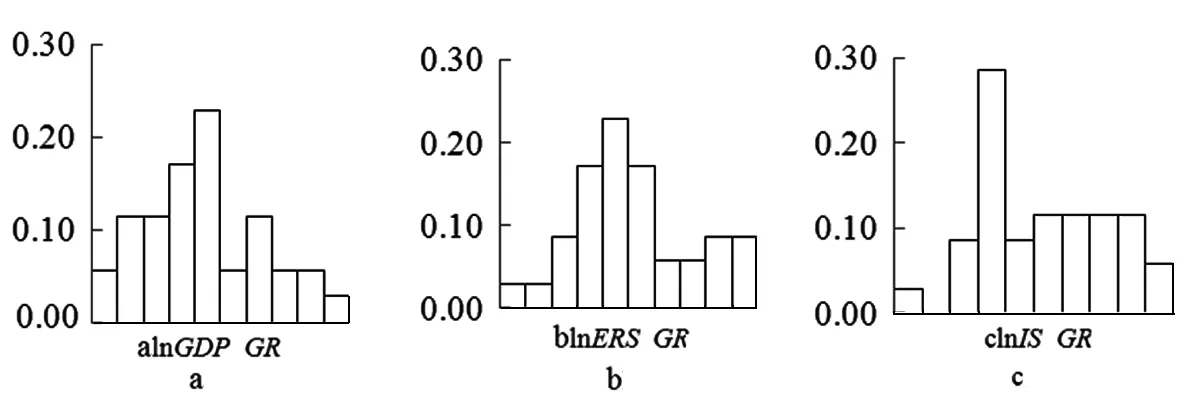
图2 影响因素对数变化率频率分布直方图
3.3 煤炭需求预测
我们首先检验蒙特卡罗方法的有效性。以1980年的各项数据为初始数据,对各输入参数进行随机抽样,计算出1981~2015年各年煤炭需求量的预测值。1981~2015年的煤炭需求实际值与预测值的结果展示如图3所示,从图中可以看出,各年的预测值与实际值吻合较好,蒙特卡罗方法拟合程度较好,可用于预测未来的煤炭需求。
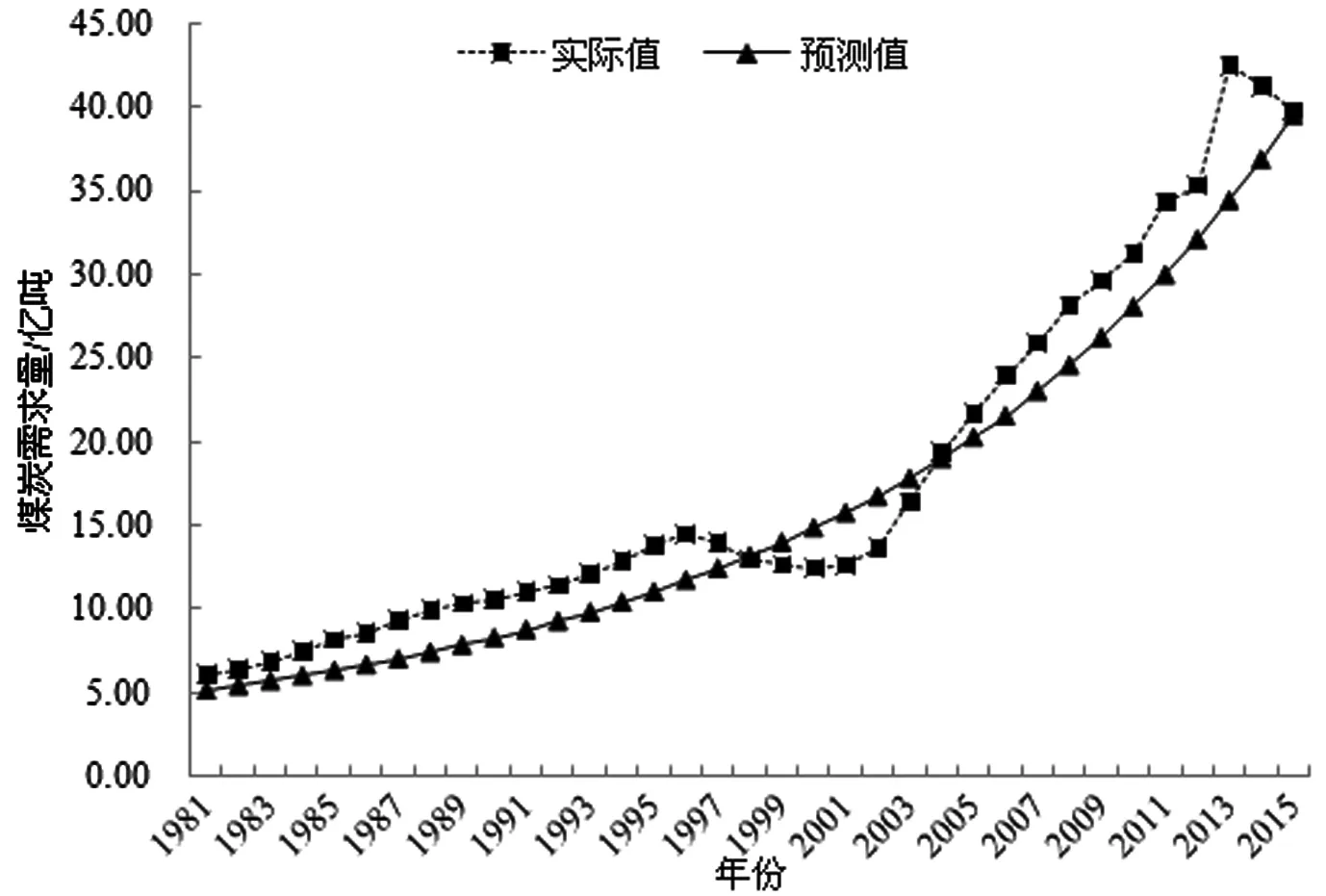
图3 1981~2015年中国煤炭需求量实际值与预测值
基于MATLAB软件,以1980年的各项数据为初始数据,控制2016~2025年的各输入参数的取值范围,对各输入参数进行随机抽样,计算出2016~2025年各年煤炭需求量的预测值,将此过程进行1000次,将各年对应的1000个预测值进行平均,得到2016~2025年稳定的煤炭需求预测值,各年的预测量如图4所示。

图4 2016~2025年中国煤炭需求量预测值及其增长率
从图4的预测结果可以看出,2016~2025年的煤炭需求量呈先平稳上升后快速下降趋势,并于2020年达到需求的峰值40.25亿吨。2016~2020年期间,前四年煤炭需求量平稳增长,平均增长率约为0.53%,最后一年增长率骤降至0.10%,并于2020年增长到峰值40.25亿吨。2021~2025年期间,前两年煤炭需求量平稳下降,平均下降率约为0.36%,后三年下降幅度越来越大,平均下降率约为0.84%,并于2025年下降到38.96亿吨。
3.4 预测结果的比较
为检验预测效果,将采用蒙特卡罗方法的预测结果与近期的煤炭需求预测研究高俊莲等的LEAP模型[7]以及刘畅和孙超的组合预测模型[8]的预测结果进行对比,对比的结果如图5所示。
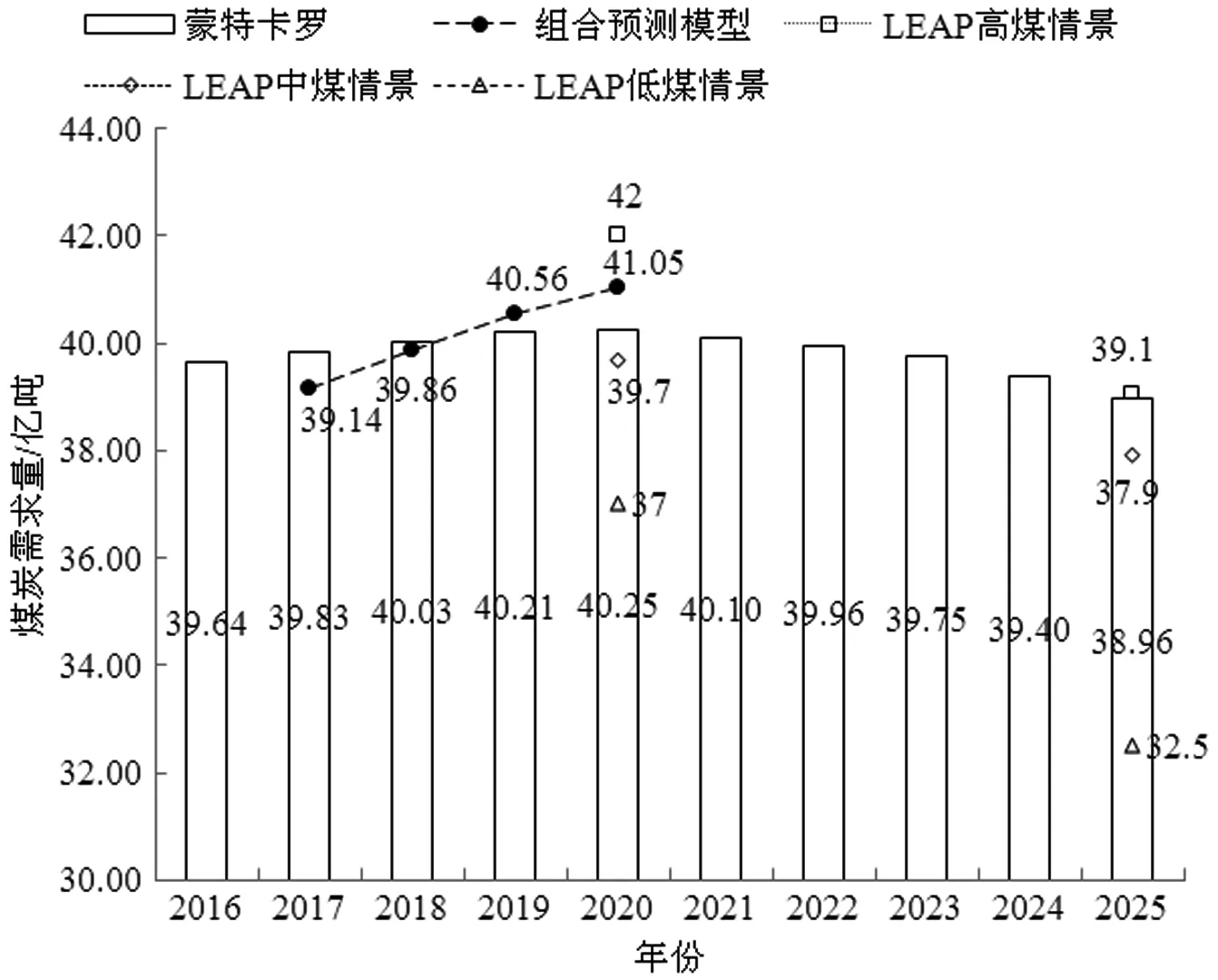
图5 MC与组合预测模型及LEAP模型的预测结果对比
从图5的对比结果可以看出,MC预测的煤炭需求量与组合预测模型和LEAP模型的预测值相近,且呈现相同的趋势。与LEAP模型相对比,MC可用于连续预测,而LEAP模型只能对特定的年份基于情景假设进行预测,无法显示煤炭需求的详细变化趋势。2020年,MC的预测结果接近于LEAP模型的中煤情景预测结果,从短期来看,清洁煤技术和煤化工发展较为缓慢,不能满足国家的大气控制目标,而可再生能源的迅速发展以及天然气对散煤的替代却可以满足。这与《国民经济和社会发展第十三个五年规划纲要》、《能源发展“十三五”规划》和《煤炭工业发展“十三五”规划》的提出的目标相一致。从整体上来看,中国经济发展步入新常态,能源需求增速放缓。从能源结构优化调整来看,中国政府加快散煤治理步伐,稳步推进可再生能源发展,积极推广应用清洁煤技术,大力发展煤炭洗选加工,到2020年,煤炭消费比重进一步降低,消费量控制在41亿吨以内,年均增速为0.7%,煤炭需求呈缓慢增长趋势,比本文的预测结果稍高。2025年,MC的预测结果接近于LEAP模型的高煤情景预测结果,从长期来看,清洁煤技术和煤化工发展较好,可以实现国家大气环境目标,可再生能源与天然气对煤炭的替代作用减小。与组合预测模型相对比,MC的预测结果更为平稳,但二者整体趋势一致。2017和2018年,组合预测模型的预测结果小于MC的预测结果,2019和2020年,组合预测模型的预测结果大于MC的预测结果。2017~2020年间组合预测模型的预测结果整体上呈现较大的增长幅度,且预示2020年以后煤炭需求仍有可能会呈现上升趋势,不会下降,这与MC的预测结果不一致。
从图6的预测值与实际值对比结果可以看出,2016年的预测值比实际值略高,这可能是由于国家为实现环境目标强制煤改气造成煤炭需求非正常减少,煤炭需求下降的同时,天然气面临供应不足的尴尬境地,进而导致北方地区供暖延缓以及供暖成本上升等社会问题。2017年的前三季度煤炭消费量比2016年的前三季度高,而第四季度一般是煤炭需求较大的季度,因此2017年的煤炭需求必然成上升趋势,这与MC预测的趋势一致。
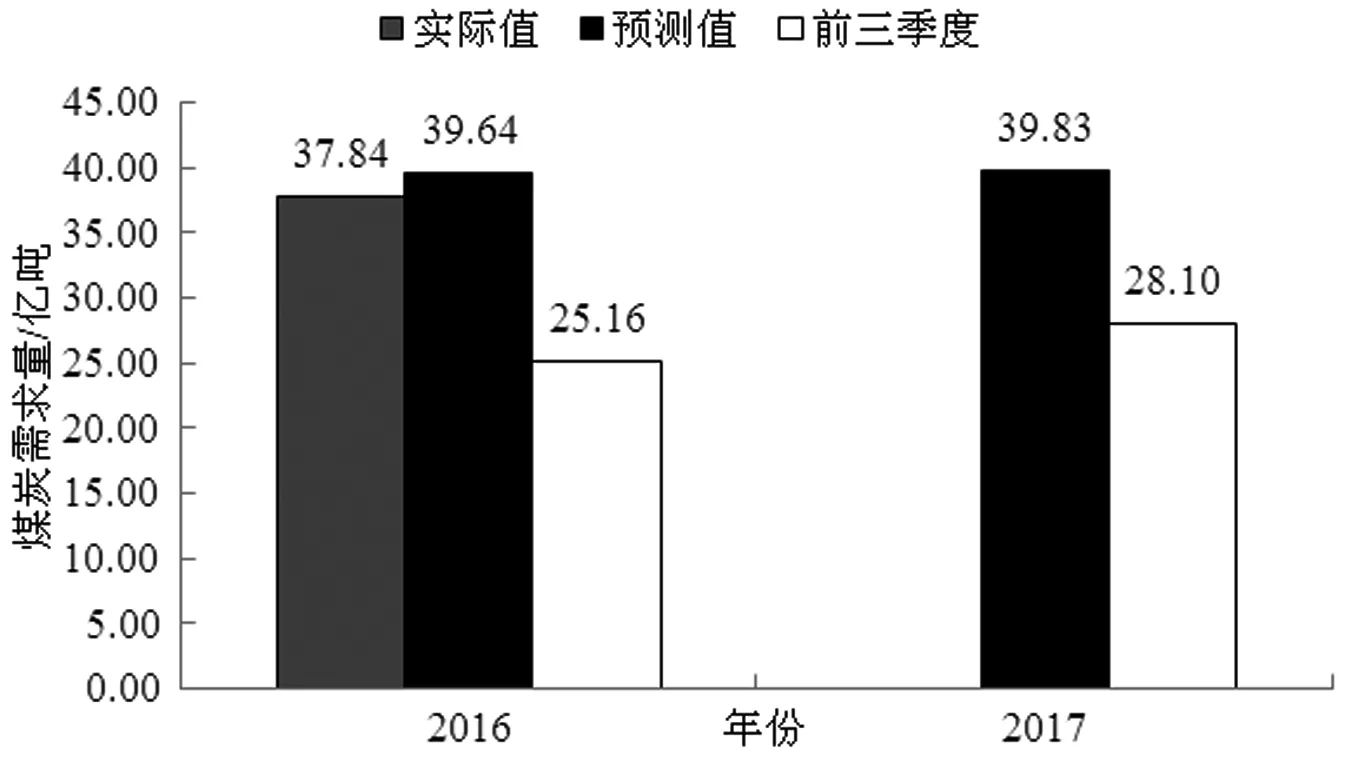
图6 实际煤炭需求与预测结果对比
4 结论
基于蒙特卡罗仿真预测,我们得到2016~2025年的煤炭需求呈先平稳增长后快速下降趋势,并于2020年达到需求的峰值40.25亿吨。由于煤炭消费的惯性,中国对煤炭还有一定的依赖性,中国煤炭的消费量在未来几年内还是呈上升趋势,但是到2020年以后中国的煤炭消费量会逐渐减少,这一趋势能够对国家减排和国家能源结构调整进行支撑。
