有服务时长和服务可选择性的快递车辆调度在线策略研究
2020-10-23马军平徐寅峰吴腾宇
马军平,徐寅峰,吴腾宇
(1.西安工业大学 经济管理学院,陕西 西安 710032; 2.西安交通大学 管理学院,陕西 西安 710049; 3.重庆邮电大学 经济管理学院,四川 重庆 400065)
0 引言
2018年6月中国国家邮政局在《2017年邮政行业发展统计公报》中指出,2017年,中国邮政行业业务总量突破9000亿元,收入突破6000亿元。其中全年快递服务企业业务量完成400.6亿件,同比增长28%;快递业务收入完成4957.1亿元,同比增长24.7%。对于快递企业来说,其收益主要来自揽件服务,因此,为了达到更高的收益水平,实现对快递揽件车辆进行有效调度(例如投递路线智能优化技术、运输管理全程跟踪查询技术等),具有重要的现实意义。
在实际揽件过程中,快递车辆的行驶路线调度具有两个显著特征:一是无法提前获知顾客发快递的需求;第二个是需求的到来时间和地点难以预测,甚至难以给出其分布概率。这是一个典型的在线决策问题,即决策者在只知道部分信息的情况下需要做出全局优化决策的问题。该问题在理论上可以用在线旅行商模型进行刻画,但是以往的在线旅行商模型尚未考虑快递揽件情境的特殊性,例如,服务每一个快递需求需要花费一定的时间(如填写面单,收取服务费等时间),并且,有时快递车辆因时间、容量、距离等原因有可能拒绝新的快递请求从而导致损失(如经济损失、企业声誉损害或者产生顾客抱怨等)。因此,针对上述情形,本文提出带有服务时长和服务可选择性的快递车辆在线调度问题,建立在线优化模型,设计相应的快递车辆在线调度策略并且在理论上分析其竞争比,结论将为快递车辆的科学调度提供理论依据。
需求出现的时间和位置等信息不确定的在线旅行商问题最早由Ausiello等在2001年提出。Ausiello等在一般网络上给出了2-竞争比的在线策略,在直线上给出了1.75-竞争比的在线策略[1]。后来的学者在此基础上对在线旅行商问题进行扩展,例如:在线PCTSP问题[2]、具有可选择性的在线旅行商问题[3,4]、带有预知时间的在线旅行商问题[5~10]、特殊网络上的在线旅行商问题、基于时间约束的在线旅行商问题[11,12]等。其中具有可选择性的在线旅行商问题是指在线车可以选择拒绝服务需求,但是拒绝需求将付出一个惩罚[3]。Jaillett和Lu对此问题进行了研究,并在正半轴上给出了一个2-竞争比的在线策略,在一般网络上给出了一个2.28-竞争比的在线策略[3]。他们后来又研究了具有实时可选择性的在线旅行商问题,即当一个新的需求到达时,在线策略要立即做出选择接受或者拒绝该需求的决策,并在正半轴上给出2.5-竞争比的在线策略,在直线上给出3-竞争比的在线策略[4]。在此基础上,温新刚等研究了具有时间约束和服务可选择性的在线旅行商问题[11],廉文琪等研究了基于预知信息和实时服务选择的在线旅行商问题[12]。以上研究中均假设服务需求的服务时长为零,即在线车经过需求点即视为服务完成,这使得以往提出的车辆在线路径选择策略不再适用于本文所研究的情形。因此,同时考虑服务时长和服务可选择性的快递车辆在线调度问题,应当如何建模并设计相应的在线策略,在理论上需要进一步研究。
本文克服以往模型中未同时考虑服务时长和服务可选择性的不足,在理论上是对已有研究的深入和扩展,并且更加符合快递车辆实时调度的现实。后续行文首先进行问题描述并证明了该问题在线策略竞争比的下界;然后在正半轴上,提出了Replan策略并证明其竞争比;在直线上,提出了ReOPT策略并证明其竞争比;在一般网络上,提出了GRH策略并证明其竞争比;最后给出实例和结论。
1 问题描述与基本定义
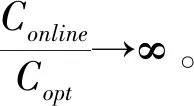
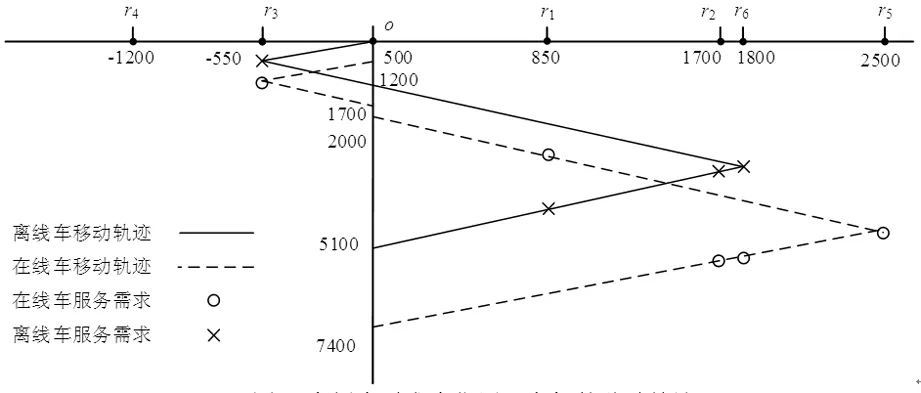
带有服务时长和服务可选择性的快递车辆在线调度问题描述如下。给出一个网络图M,d为定义在M上两点间的距离函数d(.,.)。网络图M具有三个属性:(1)M是对称网络,即对于M上的任意点对x,y,均满足d(x,y)=d(y,x);(2)对于M上的任意一点x,满足d(x,x)=0;(3)网络图M满足三角不等式。该网络图M包括一个起点o和一系列可能出现需求的节点。将需求表示为Ri=(li,ri,pi,si),i=1,2,3,…,n,其中n为需求的总数量。li∈M表示需求i的位置,ri≥0表示需求的释放时间(release time),只有到达释放时间的需求才可以接受服务,并且ri具有时间顺序,即当i 0时刻,一个在线车处于起点o。在线车事先不知道需求的数量n,当需求释放后,在线车才能获知需求的位置和服务时长。当一个新的需求被释放时,在线车需要决定是否接受该需求。车辆只能保持静止或以单位速度移动来服务已接受的需求,在线车最终状态为处理完所有需求后在起点o静止。将车辆最早进入最终状态的时间定义为完工时间(makespan)。该问题的目标是服务需求的总成本尽可能小,其中总成本是指完工时间与惩罚之和。 情形2r1≤t0≤rn+1。令m∈{1,2,…,n},设在线车离开起点o的时间t0满足rm≤t0≤rm+1。当在线车从起点o出发时,离线敌手只能释放前m个需求。 由以上分析可以得到: 否则令k(k≤m)为接受的需求中距离起点o位置最远的一个需求,则在线车的成本为 因此,由以上分析可得: 3.1.1 正半轴上的最优离线策略A 为给出正半轴上的在线策略,首先在正半轴上考虑如下离线问题:即不考虑释放时间的带有服务可选择性和服务时长的车辆调度问题。假定一个车辆位于x位置(x≥0)并且有n个需求(li,pi,si)1≤i≤n需要服务。车辆只能保持静止或以单位速度移动来服务已接受的需求并且最后返回起点o。目标是服务需求的总成本尽可能小,其中总成本是指完工时间与惩罚之和。 引理1正半轴上不考虑释放时间的带有服务可选择性和服务时长的车辆调度问题最优离线策略的总成本满足下列条件: 证明分两种情形讨论: 引理得证。 从引理1的分析可以得出,当车辆处于x位置(x≥0)时,可提出一个解决不考虑释放时间的带有服务可选择性和服务时长的车辆调度问题的最优离线策略A,该策略根据车辆处于x位置,分为两种情形,具体描述如下。 策略A(x≠0) 步骤1将所有的需求非递减排序满足lki≤…≤lkn。令1≤m≤n使得lkm≤x≤lkm+1。如果不存在这样的m,令m=0,转步骤 2。 策略A(x=0) 步骤1将所有的需求非递减排序满足lki≤…≤lkn。令1≤m≤n使得lkm≤x≤lkm+1。如果不存在这样的m,令m=0,转步骤2。 3.1.2 正半轴上在线策略Replan策略及其分析 在策略A的基础上,针对带有服务时长和服务可选择性的快递车辆在线调度问题,本文提出正半轴上的在线策略Replan策略。该策略的主要思想是每当一个新的需求被释放时,在线车根据当前的位置的情况,选择调用策略A。 Replan策略在线车根据当前的位置x进行决策: 步骤1初始化。令x=0,初始时间t=0,迭代次数i=0,转步骤2。 步骤2如果没有新的需求释放,停止:拒绝任何以前未服务的需求,则完工时间(makespan)为t。否则,另i=i+1,在线车在起点o静止到下一个需求释放的时间ri,转步骤3。 步骤3如果x>0,则在线车调用策略A(x≠0),否则调用策略A(x=0),此进,ω=ri-t,然后根据计算出的路径服务接受的需求,令按照该路径移动返回起点o的时间为tr。转步骤4。 步骤4如果在线车在完成当前路径(未到达起点o)之前没有新的需求释放,则设x=0,t=tr,转步骤2。如果在线车在未完成当前路径(未到达起点o)时就释放了新的需求,令i=i+1,根据新需求出现的时间更新在线车当前的位置x和t,转步骤3。 证明根据离线服务器的行动决定在线车的行动,不失一般性,令最后一个释放的需求为第n个需求。 情形2.2x≥lm。令Lmax为当前路径上距起点o最远的需求的位置。令S′为离线车未接受而在线车在一次和第二次通过lm位置之间接受的需求集合。 在情形2.2下,在线车的成本为: 由情形2.1的分析,可知在情形2.2下,在线车成本与离线车成本之比为: 定理得证。 3.2.1 直线上的最优离线策略B 在直线上,带有服务时长和服务可选择性的快递车辆在线调度问题对应的离线问题可以描述如下。在一条直线上已经释放了n个需求(li,pi,si)1≤i≤n,不失一般性,假定离线车位于x≥0处。离线车只能保持静止或以单位速度移动来服务已接受的需求并且最后返回起点o。目标是服务需求的总成本尽可能小,其中总成本是指完工时间与惩罚之和。 因此,离线车只要在满足下列三个条件的需求中选择相应的需求构成实际服务的需求集合S,使得离线成本最小即可。 (1) 由以上分析,可以给出直线上带有服务时长和服务可选择性的快递车辆在线调度问题对应的最优离线策略B。 3.2.1 直线上在线策略ReOPT策略及其分析 在直线上最优离线策略B的基础上,针对带有服务时长和服务可选择性的快递车辆在线调度问题,给出直线上的在线策略ReOPT策略。 ReOPT策略 在线车根据当前的位置x进行决策: 步骤1初始化。令初始时间t=0,迭代次数i=0,转步骤2。 步骤2如果没有新的需求释放,停止:拒绝任何以前未服务的需求,则完工时间(makespan)为t。否则,另i=i+1,在线车在起点o静止到下一个需求释放的时间ri,转步骤3。 步骤3在线车调用离线最优策略B,然后根据计算出的路径服务集合S中的需求,令按照该路径移动返回起点o的时间为tr。转步骤4。 步骤4如果在线车在完成当前路径(未到达起点o)之前没有新的需求,释放则t=tr,转步骤 2。如果在线车在未完成当前路径(未到达起点o)时就释放了新的需求,令i=i+1,根据新需求出现的时间更新t,转步骤3。 定理3对于带有服务时长和服务可选择性的快递车辆在线调度问题,ReOPT策略在直线上的竞争比为2。 证明在线车根据离线服务器的行动决定自身的行动,不失一般性,令最后一个释放的需求为第n个需求。 情形2离线车接受了最后一个需求n。令S为离线车所有接受的需求集合,令S位于区间[-L,R]之内。令P(t)为在线车在t时刻的位置,则将rn时刻在线车的位置记为x=P(rn)。 假设策略C是一个针对不考虑释放时间情形下,带有服务可选择性和服务时长的快递车辆在线调度问题的离线策略。令Sm为策略C在前m个需求中接受的需求集合,该集合包括起点o。策略C可以计算出一条服务Sm中需求的服务路径。对于每一个新的需求释放的时刻tm(m≥1),在线策略调用策略C来计算该服务路径。 GRH策略(Greedy return home)的主要思路是一旦有新的需求出现,在线车就通过最短路径返回起点o以便于可以尽快调用策略C重新计算一条服务路径。这里的Greedy是指在线车总是通过最短路径在两个需求点之间移动。 GRH策略每次一个新需求m在rm时刻被释放时,在线车根据这个需求是否被策略C接受决策行动: 情形1m∉Sm。在线车忽略该需求,继续保持当前路径; 情形2m∈Sm。在线车通过最短路从当前位置返回起点o,然后调策略C计算一条服务路径Tm。然后沿着路径Tm服务集合Sm中的所有需求,直到新的需求出现或最终返回起点o。 首先给出引理2,在此基础上证明GRH策略的竞争比。 定理4对于带有服务时长和服务可选择性的快递车辆在线调度问题,GRH策略在一般网络上的竞争比为2.5。 从定理2~定理4的结果可知,Replan策略是一个最优的在线策略,ReOPT策略和GRH策略的竞争性能较优。本研究与传统的在线旅行商问题相比,克服其模型中未考虑需求点服务时长和服务可选择性的不足,在理论上证明了考虑服务时长能够改善在线策略的竞争性能。因此,本文对在线旅行商问题在理论上给出了更一般化的模型,提出的在线策略也更加符合快递车辆运营的实际情形。 某国内快递公司DB物流西安东郊分部负责的长乐东路沿途分布着20家单位(用实心圆点标记),该分部的集货点位于长乐路中段(用圆圈标记),见图1。每一家单位均有可能有发快递的需求,但是快递车辆根据实际情况,可以选择接受或拒绝该需求。如果快递车辆接受该需求,则服务这个需求要花费一定的服务时长。如果快递车辆拒绝该需求,则需要付出相应的惩罚。某日快递公司收到用户的发货请求r1~r6的出现时间分别为t1=0,t2=200,t3=500,t4=1500,t5=2000,t6=2900。0时刻时,快递车位于起点o处。对于快递揽件车辆而言,揽件需求是依次出现的,快递车辆无法事先获知快递需求将在何时何处出现。那么,快递车应如何选择路径,使得从集货点出发服务所有需求并返回集货点的总成本(makespan+惩罚)最小? 图1 DB物流公司西安长乐东路揽件需求点分布 不失一般性,假设快递车以单位速度移动来服务需求,快递车服务每个需求点的服务时长为100个距离单位,快递车辆拒绝每个需求点的惩罚为1400个距离单位。为分析方便,将上述需求点的出现次序和位置在直线上标出(图2)。 先分析在线情形。假设在线车采用直线上的ReOPT策略来调度车辆。当每一个需求出现时,在线车的决策和移动过程如表1。经计算,在线车最终实际的服务路径是o-r3-o-r1-r5-r6-r2-o,总的服务成本为8800。 表1 在线车路径选择决策过程 再分析离线情形。在离线情形下,在0时刻时,快递车已知道所有需求点的未来的位置和释放时间。经计算,离线车的最优路径为:o-r3-o-r6-r2-r1-o。在t=o时刻时,离线车即从起点o出发,在移动的过程中服务沿途已释放的需求,其所花费的总成本为7900(离线车和在线车的移动轨迹如图2所示) 图2 实例中需求点位置及车辆的移动轨迹 综上,本实例中,ReOPT策略的实际竞争比为8800/7900=1.114,优于ReOPT策略竞争比下界的理论值2,这说明ReOPT策略在现实中实用性较好。这是因为本问题在线策略的下界是指当需求以最坏情形出现时,在线策略有可能达到的最好情况。但是现实中的快递需求序列出现最坏序列的可能性较小。 针对快递揽件需求出现具有不确定性、服务每一个快递需求需要一定的服务时长,且拒绝快递需求会受到一定的惩罚的情形,提出针对带有服务时长和服务可选择性的快递车辆在线调度问题。对此问题在线策略竞争比的下界进行了证明,并且对网络是正半轴、直线和在一般网络的情形,设计了相应的在线策略并且证明在线策略的竞争比。与一般在线旅行商问题比较,本文建立了更为一般的模型和在线策略,是对已有研究的扩展。所提在线策略在实际中具有实用性,可为快递车辆的科学调度提供理论依据。对于在线车到达需求点时才能获知该需求的服务时长的情形,未来可以进一步研究。2 在线策略竞争比下界
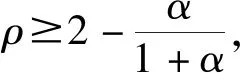
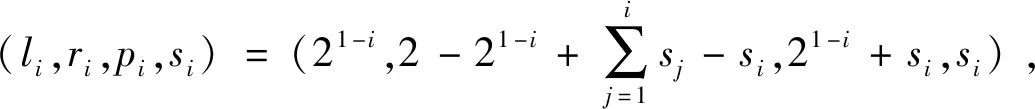
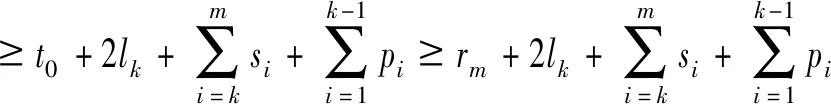

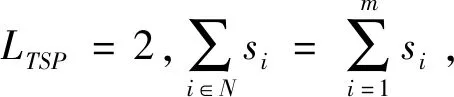
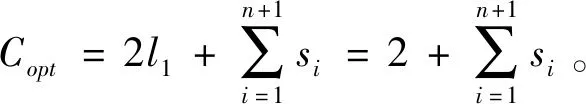

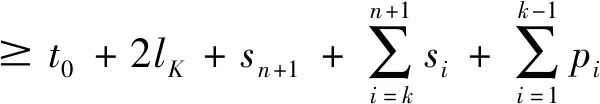

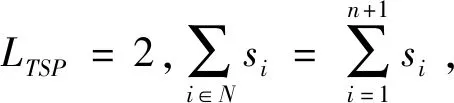
3 快递车辆调度在线策略
3.1 正半轴上的在线策略
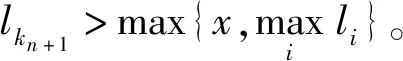
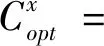
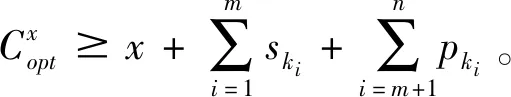
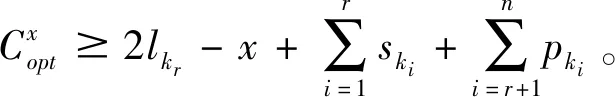
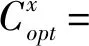
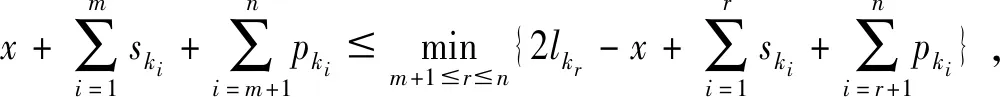
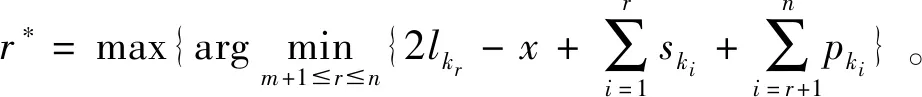
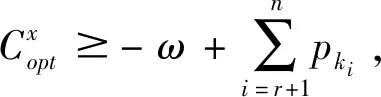
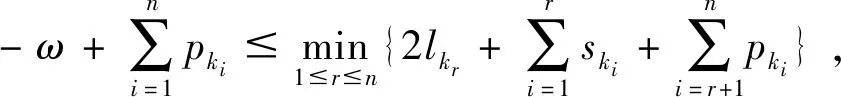
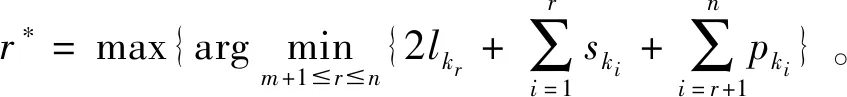
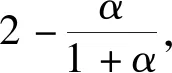




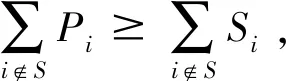

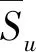
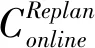
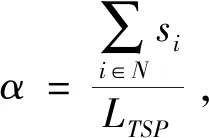
3.2 直线上的在线策略
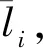
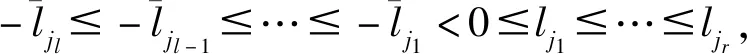
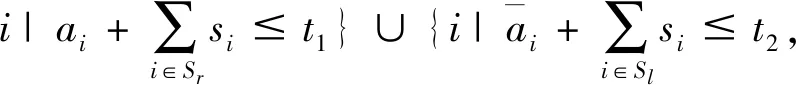
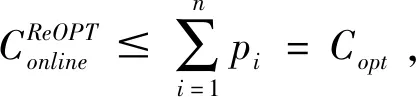

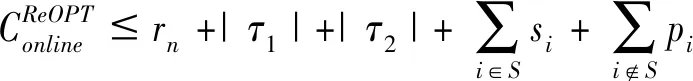

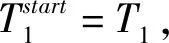
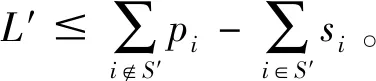
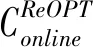
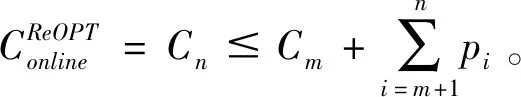
3.3 一般网络上的在线策略
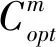

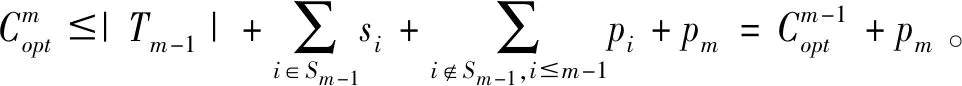
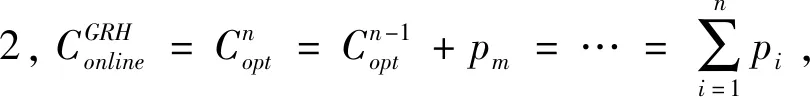
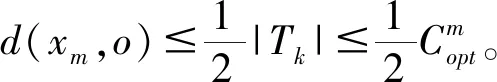
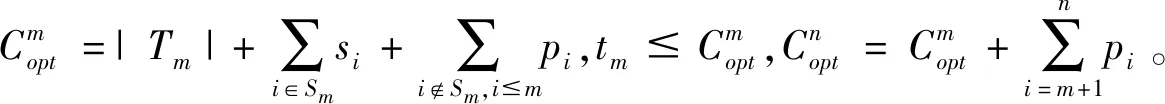
4 实例分析


5 结论
