中央与地方政府PM2.5治理策略分析
2020-10-23邢瑶瑶于晓辉谭志斌
周 珍,邢瑶瑶,林 云,于晓辉,谭志斌,王 洁
(1.首都师范大学 管理学院,北京 100089; 2.北京理工大学 能源与环境政策研究中心 100081; 3.北京物资学院,北京 101149)
0 引言
党的十九大报告提出加快生态文明体制改革,建设美丽中国,首当其冲的是着力解决突出的环境污染问题。已有研究[1~3]发现,治霾主要有三方面的影响:(1)PM2.5浓度降低会减少呼吸系统等疾病的发病率及死亡率,给民众带来健康收益;(2)企业需要投入成本,以保证污染去除设备的投入和运转;(3)环境规制会影响企业的产能,对当地的经济造成影响。文献[4~7]研究在治理CO2的同时具有SO2、NOX等污染物浓度降低的协同效应,且协同效应具有空间异质性。例如,地区间由于能源消费结构与人口密度的不同,CO2治理的协同效应存在地区差异。只有了考虑了污染物治理的空间异质性协同效益,相应的政策的设计才具有配置效率。同样的,在PM2.5治理中,由于各地区GDP、产业结构、人口数量等差异,治霾给民众、企业以及政府带来的协同效益均存在空间异质性。例如,在北京去除1单位PM2.5与在河北去除1单位PM2.5所需要的直接治理成本、带来的民众健康收益以及经济发展影响会存在很大的差异。因此,PM2.5合作治理的政策设计需要考虑污染治理给民众、企业、政府等多主体带来的多方效益,只有这样才可能使治理污染投入的资源在地区间达到最优配置。
另外,现有研究多借鉴基于总量控制原则的CO2减排建立空气污染治理博弈模型,论证了雾霾合作治理比非合作治理成本更低[8,9]。总量控制指的是:只要其中一个地区达到了整个区域的去除量目标,就认为整个区域的所有地区均达标。由于PM2.5的浓度过高会对当地的民众的健康带来危害,中国政府在2012年颁布了《大气污染防治行动计划》,明确要求各地区PM2.5的浓度在规定时间内要下降到规定标准,因此总量控制不适合PM2.5治理。例如,总量控制下,相邻地区减排1单位对本地区的贡献等于1单位。而在浓度控制下,由于跨界传输率的不同,相邻地区1单位的减排对本地区的贡献少于1单位。因此,本文探究基于浓度控制的PM2.5治理,在减排指标约束下的合作治理是否一定优于非合作治理?减排指标的设置对局中人治理策略选择有何影响?局中人的策略选择对污染物的整体减排量又有何影响?本文将对上述问题进行理论与方法探究,并在京津冀区域对治理模型做实证分析。
2 模型准备
2.1 PM2.5浓度与质量的转换关系
设当年PM2.5的生产量和去除量分别为Oi,Pi,去年生产量和去除量分别为Oia,Pia,则地区i相对于去年的PM2.5减排量为(Oi-Pi)-(Oia-Pia)。设地区i的PM2.5减排影响到地区j的比例为δri,当i=j时,表示本地影响。那么,假设区域内共有n个地区,地区i空气中的PM2.5当年的减少量Pri可以表示为:
Pri=δ1i[(O1-P1)-(Oia-P1a)]+
δ2i[(O2-P2)-(O2a-P2a)]+…+
δni[(On-Pn)-(Ona-Pna)]
(1)
记每个地区空气中PM2.5浓度与质量之间存在转换关系为φi,则PM2.5空气中的减少量Pri与下降浓度εi的关系为:
εi=Pri·φi
(2)
2.2 PM2.5综合治理成本函数的建立
接下来本文通过分别建立PM2.5治理的民众健康收益、经济发展影响以及直接治理成本函数来构建PM2.5综合治理成本函数。
(1)民众健康收益函数构建
本文参考文献,选取PM2.5造成的呼吸系统疾病、心血管疾病、儿科、内科、慢性以及急性支气管炎、哮喘以及急性效应与慢性效应死亡这九项作为疾病终端,将PM2.5治理前的健康成本减去PM2.5治理后的健康成本作为治理PM2.5所带来的健康收益,即民众健康收益。参考文献[10~14]的环境健康价值评估模型以及PM2.5的浓度与质量之间的转换关系,建立PM2.5的去除量与单位人口的健康效应变化量的关系如式(3)所示:
ΔEij=Ij0{[1-exp(βj(ρi-(Pi-Pia)φi))]-
[1-exp(βj(ρi-ρo))]}
(3)
本文采用疾病成本法[12]对治理PM2.5带来的呼吸系统疾病、心血管疾病、儿科、内科、急性支气管炎以及哮喘这六种疾病的健康收益价值进行评估,采用伤残调整生命年法[13]估计地区治理PM2.5带来的慢性支气管炎的健康收益价值,使用调整人力资源法[14]对PM2.5带来的慢性及急性死亡的健康收益价值进行评估。则地区的民众健康收益函数为:
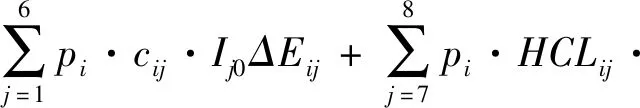
Ij0ΔEij+pi·cij·Ij0·Dalysi·ΔEij
(4)
其中,pi表示地区i当年的常住人口,cij表示地区i第j个疾病终端的单位病例成本,HCLij表示地区i第j个疾病终端的基于人均GDP的个人人力资本;Dalysi表示第j个疾病从发病到死亡所损失的全部健康寿命年。
(2)经济发展影响函数构建

根据2015年地区减少的PM2.5浓度计算得到2015年空气中PM2.5浓度降低1ug/m3带来的损失ΔEi=Ei/Pi2015。则地区i的经济发展影响函数为:
Cie=ΔEi·Pi·τ(τ为时间因子)
(5)
(3)直接治理成本函数构建
本文将PM2.5的治理转换为两种关键前体物SO2与NOX的治理。记地区iPM2.5质量与SO2和NOX质量的转换系数分别为μiSO2,μiNOx,下面分别建立SO2与NOX的去除成本模型。
根据曹东等[15]构建的污染物去除成本函数,建立SO2去除成本模型如下:
(6)
其中,CiSO2为地区iSO2的去除成本,Wi为地区i的废气排放量,PiSO2为地区i的SO2去除量,θ,φ,μ均为待确定参数。
根据文献[16],记NOX去除量与去除成本之间的线性关系系数为σi,地区i的NOX去除成本函数为:
CiSO2=σi·PiNOx
(7)
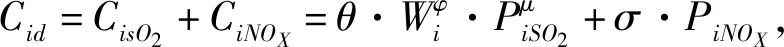
(8)
综上所述,地区i治理PM2.5综合治理成本为该地区的直接治理成本加上治理PM2.5的经济发展影响再减去民众健康收益,即:
Ci=Cid+Cie-Rih
(9)
3 PM2.5治理博弈模型
3.1 PM2.5非合作治理模型
对于PM2.5的减排有两种方式,一是去除工业上的污染物,二是去除民众生活中排放的污染物,如利用限行等措施减少汽车尾气排放的PM2.5。研究表明,生活去污的单位成本远高于工业去污[17],因此,各地区优先考虑工业去污方式。
确定治理成本之前,通过比较地区iPM2.5最大降低浓度εi与中央政府给该地区规定的PM2.5浓度ri之间的关系,来判断地区i依靠工业去污能否达到本地的治理目标。在单独治理时各地区之间的信息不沟通,无法确定其他地区的去除量,因此,假设其他地区的去除量与去年相等,因此式(1)可以简化为:Pri=δii[(Oi-Pi)-(Oia-Pia)]。则该地区空气中PM2.5最大下降浓度εi=φi·δii[(OPi-PPi)-(Oia-Pia)]。
那么,通过式(10)可以判断地区i依靠工业去污能否达到本地的治理目标:
φi·δii[(Opi-Ppi)-(Oia-Pia)]≥ri
(10)
如果满足式(10),则直接使用PM2.5单独治理成本优化模型确定本地治理策略,详见3.1.1;否则,需要通过其他渠道来完成空气中PM2.5的减少目标,详见3.1.2。
3.1.1 地区可以依靠本地去污达标
根据上文分析,此时地区i首先满足式(10);其次,地区i的去除量不能超过本地区的最大去除量PPi,即:0≤Pi≤PPi。因此,地区iPM2.5单独治理成本优化模型为:
(11)
3.1.2 地区无法依靠本地去污达标
此时,由于工业去污成本较低,地区i首先将去除能力内的工业污染去除完毕,记该部分成本为Civ,能够降低的PM2.5浓度为φi·δii[(Opi-Ppi)-(Oia-Pia)];而未达标的剩余浓度为ri-φi·δii[(Opi-Ppi)-(Oia-Pia)],这部分PM2.5浓度的降低有两种方案:
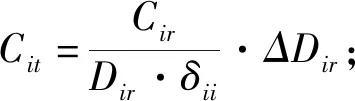
(2)购买邻近地区的去除量:通过降低邻近地区的污染传输量来达到本地PM2.5浓度下降目标,支付的成本为邻近地区治理这部分PM2.5所需的直接治理成本与经济发展影响,记该成本为Cib,购买的去除量可通过式(12)求解得到:
(12)
其中,第一个约束条件表示地区j的减排传输到地区i的量能够使得地区i完成自己工业去除能力外的减排目标,第二个约束条件表示地区j的去除量要介于去年的去除量与该地区去除量上限之间。
地区i剩余减排目标的治理策略为最小成本方案所对应的策略,相应的成本为:Cis=min{Cit,Cib}。因此,地区i无法依靠本地去污达标时总成本为Ci=Civ+Cis。
上述模型帮助各地区在单独治理时选择治霾策略,当各地区按照这种策略进行减排时,需要重新计算各地区受到的来自所有地区减排带来的民众健康收益,各地区均得到一个实际的综合治理成本。
3.2 PM2.5治理合作博弈模型
设合作联盟为S=(1,2,…,m)⊆N,当m=n时,为全局合作。合作联盟内的各地区之间的信息共享,可以共同确定联盟内各地区的减排量,而对于联盟外的地区,则无法确定其他地区的去除量,因此,假设联盟外地区的去除量与去年相等,因此式(1)可以化简为:
Pri=δ1i[(O1-P1)-(O1a-P1a)]+
δ2i[(O2-P2)-(O2a-P2a)]+…+
δmi[(Om-Pm)-(Oma-Pma)]
同样地,可以由式(13)判断合作联盟依靠工业去除污染物是否可以达到联盟内地区的减排目标:
Pri≥ri
(13)
如果满足式(13),那么使用PM2.5治理合作博弈模型来确定合作联盟的成本;否则,类比3.1.2,需要通过其他渠道来完成空气中PM2.5的减少目标。
对于PM2.5治理合作博弈模型,各地区首先需要满足式(13);此外,各地区的去除量应该满足不超过本地区的最大去除量,即:0≤Pi≤Ppi,i=(1,2,…,m)。
因此,PM2.5治理合作博弈模型为:
(14)
根据上述模型可以得到各地区在不同合作情形下的治霾策略,以及重新计算民众健康收益后各个地区的综合治理成本。
4 京津冀PM2.5治理实证分析
4.1 京津冀PM2.5非合作治理实证分析
京津冀各地区出台的大气污染防治工作方案中,设定了2017年本地的PM2.5浓度下降目标:北京相对于2016年PM2.5浓度要降低18%,天津13%,河北6%,相应的PM2.5减少浓度分别为13ug/m3、9ug/m3以及4ug/m3[18,19]。本文以京津冀区域完成2017年的去除目标作为研究对象,研究京津冀各地的直接治理成本、健康收益、经济损失等[11~16],分别从中央政府与地方政府视角对局中人PM2.5治理策略的意向进行分析。
4.1.1 北京单独治理PM2.5
当北京单独治理PM2.5时,根据式(10)可以判断,将北京去除量的上限即15.64万吨全部去除掉仅仅能够降低10.35ug/m3的PM2.5,这距离北京的PM2.5降低目标13ug/m3还差2.65ug/m3,这意味着北京依靠工业去污无法达到PM2.5下降目标。根据3.1.2,对于工业去污无法达标的部分,两种去污方案及其成本分别为:
(1)民用去污:根据赵峰侠等[17]的研究,北京市限行一年可以减排SO20.2万吨,造成直接经济损失84亿元/年,因此,减排1万吨PM2.5的成本为903亿元,Cit=5775075.53万元。
(2)购买邻近地区去除量:根据式(11)的求解得到,河北地区在本地去除81.80万吨PM2.5,能够使北京地区达到减排目标,此时北京需要支付的成本最小:C1b=1189335.04万元。
比较两种方案成本大小,北京选择向河北购买去除量。因此,北京无法单独完成治理目标,除了本地工业去污外,还需支付成本帮助河北去污以达到本地治霾目标。
4.1.2 天津单独治理PM2.5
天津单独治理PM2.5时,可以判断满足式(10),因此,天津使用PM2.5单独治理成本优化模型进行决策:

使用Mathematica 8.0对上式进行求解得到天津单独治理PM2.5时的去除量为14.63万吨。
4.1.3 河北单独治理PM2.5
河北单独治理PM2.5时,可以判断满足式(10),同理,根据式(11)并求解得到河北单独治理PM2.5时的去除量为71.15万吨。但由于北京需要河北去除81.80万吨的PM2.5才能达标,比较发现,河北本地达标需要去除污染物的量小于北京需要在河北去除的量,而北京会支付超出河北基础减排量外的直接治理成本与经济发展影响成本,因此,河北只需支付基础减排量PHa这部分的直接治理成本与经济发展影响即可,而享受的健康收益则为河北地区的实际去除量即81.80万吨带来的健康收益。
综上,各地区确定单独治理时PM2.5减排量后,重新计算民众健康收益后京津冀三地的综合治理成本分别为:北京1897785.63万元,天津1900455.48万元以及河北3683650.42万元。
4.2 京津冀PM2.5合作治理实证分析
4.2.1 北京-天津合作
根据式(13)判断,当北京和天津合作治理PM2.5时,可以使天津依靠工业去污达到去除目标,而无法使北京达标,对于剩余的污染物需要向河北购买去除量。根据3.1.2计算得到,北京需要河北达到77.95万吨的去除量。
在确定了北京-天津合作治理PM2.5的减排量以及河北单独治理的减排量之后,重新确定北京-天津以及河北的综合治理成本分别为:3700787.55万元,3723234.57万元。
4.2.2 北京-河北合作
同理,根据式(13)可以判断,北京-河北合作治理PM2.5时工业去污能够完成两个地区的减排目标,此时北京和河北使用式(14)PM2.5治理合作博弈模型来进行决策,使用Mathematica 8.0求解得到当北京和河北合作治理PM2.5时,北京需要去除PM2.515.64万吨,而河北需要去除81.857万吨。此时,天津单独治理的去除量为14.63万吨。北京-河北以及天津的综合治理成本分别为:5584153.92万元,1900357.04万元。
4.2.3 天津-河北合作
同理,根据式(13)可以判断,天津-河北合作治理PM2.5时工业去污能够完成两个地区的减排目标,此时天津和河北使用式(14)PM2.5治理合作博弈模型来进行决策,对模型求解得到天津需要去除14.28万吨PM2.5,而河北需要去除69.76万吨。此时,北京单独治理的去除量为15.64万吨,但北京无法完成减排目标,需要向河北支付1189335.04万元的成本以保证其达到81.80万吨的去除量。因此,此时天津-河北以及北京的综合治理成本分别为:5547782.8万元,1899245.1万元。
4.2.4 京津冀全局合作
京津冀全局合作治理PM2.5时,根据式(13)可以判断,依靠工业去污能够完成三个地区的减排目标,因此根据式(14)得到京津冀完全合作治理PM2.5时,总成本为7220498.32万元,此时,京津冀三地的去除量分别为:15.64万吨,13.74万吨,77.95万吨。
4.3 合作与非合作治理情况对比分析
根据前文的计算及分析,所有联盟方式的成本及去除量如表1所示。
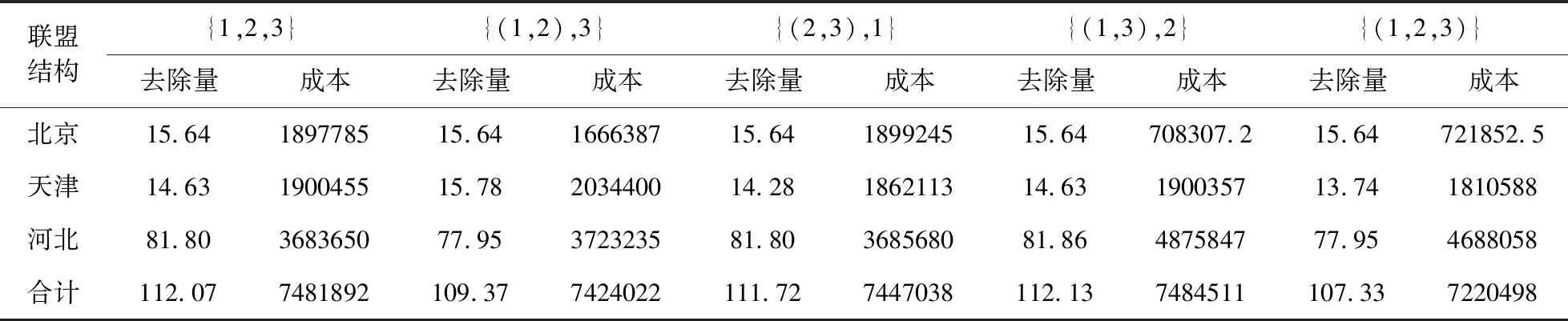
表1 不同联盟结构下去除量和去除成本比较(单位:万吨、万元)
我们发现,在浓度控制模式下,合作或非合作的治理模式会导致区域内总的PM2.5去除量以及局中人不同治理策略时区域成本均发生变化:
(1)当合作与非合作去除量一样时,合作与非合作的PM2.5治理成本无差异。这是因为考虑到地区间PM2.5的非对称性跨界传输因子,每个地区的污染治理由于对本地的贡献最大,平均单位去除成本最低,所以无论合作与否,各地区均优先选择去除本地污染物,然后再根据跨界传输因子以及平均单位去除成本选择邻近地区进行减排。此时中央政府与京津冀地方政府对于合作与非合作治理PM2.5的偏好一致,由于合作时难免会产生沟通协调成本,因此,二者此时会更倾向于选择非合作治理。
(2)当合作与非合作的去除量存在差异时,从表1可以看出,全局合作联盟的治理成本最低。这是由于合作可以使地区之间共享信息,合作联盟便可以对联盟内成员的去除量进行合理分配,以最小的去除量来完成治理目标,从而使合作治理成本比非合作时低。但另一方面,从表1可以看出,全局合作联盟的去除量也最低。相对于地,这是由于非合作时地区间信息无法共享,各地区无法得知其他地区的去除量,为了保证完成治理目标,此时各地区的减排量比合作时的多,导致了成本的上升。因此,以地方政府的视角,合作能够在完成中央政府目标的基础上更少的成本,地方政府更倾向于合作治理。而以中央政府的视角,非合作能够促使各地区在完成目标的基础上去除更多污染,带来更高的社会环境效益,使各地区更快速地达到空气质量标准,因此,中央政府更倾向于非合作治理。
(3)随着PM2.5不断得到治理,跨界传输到周围地区的PM2.5逐渐减少,因此各地区之间的跨界传输因子会不断降低,在其他条件不变的情况下,合作与非合作治理之间的总成本差距也随之降低。这是因为当减排指标及其他成本参数不变时,每个地区的污染治理对本地的贡献会更大,帮助其他地区完成减排指标的能力越小,即治理PM2.5产生的泄露越少,因此,合作与非合作的差距会缩小,由于合作治理需要付出交易成本,各级政府更倾向于采用非合作治理的方式。相反,如果PM2.5没有得到妥善的治理,某地区跨界传输到周围地区的PM2.5的量会增大,地区间的跨界传输因子也会增大,在其他条件不变的情况下,该地区帮助其他地区完成减排指标的能力也会增大,所以会增大合作与非合作治理的总成本差距,此时中央政府会希望各地区非合作治理以增加总去除量,而地区政府更偏好于合作治理以降低支付的治理成本。
5 结论与政策建议
本文考虑了PM2.5治理对民众、企业、政府带来的协同效应,构建了PM2.5治理综合成本函数;并考虑地区间的非对称的跨界传输影响,建立非合作及合作博弈的PM2.5治理模型。最后以京津冀为例,在给定减排指标下,分别从中央和地方政府的视角分析了合作与非合作治理的策略偏好,得到以下结论与相关政策建议:
(1)当合作与非合作去除量相同时,两种方式的PM2.5治理成本无差异,中央政府与京津冀地方政府对于合作与非合作治理PM2.5的偏好也一致。由于合作需要沟通成本,非合作治理为更好的选择。
(2)当合作与非合作去除量有差异时,合作治理成本更低,但区域内的总去除量也更少。京津冀地方政府更倾向于合作治理而中央政府倾向于非合作治理以增加社会环境效益。中央政府在确定各地区的减排指标时,如果能够使地区在合作与非合作时的污染物去除量一致,那么该地区就不会以降低污染物去除量为代价寻求合作治理,此时合作与非合作均能达到配置效率。
(3)随着时间推移,各地区PM2.5浓度越来越低时,地区间跨界传输因子降低,合作与非合作治理之间的总成本差距也随之降低,此时各级政府均偏好非合作治理的方式。否则,地区间的跨界传输因子增大,而合作与非合作治理的总成本差距也随之增大,此时中央政府偏好非合作治理而地方政府偏好合作治理。
(4)对于京津冀地方政府而言,在非合作治理时,北京仅仅依靠工业去除污染物无法达到PM2.5浓度减少目标,对于北京没有完成的减排目标,向河北购买去除量成本最小。在部分合作治理时,北京和天津合作治理PM2.5也无法仅仅通过去除工业污染物达到北京地区的PM2.5浓度减少目标,只有合作联盟中有河北的情况下,北京才有可能通过工业去除污染物完成本地的PM2.5浓度减少目标。这说明当前的指标设置会促使北京自觉帮助河北减排,但当前在北京的帮助下,河北并没有完全去除掉本地污染物,因此各地区的减排指标设置应该考虑各地区的经济能力,并进一步研究如何设置指标能够使河北在北京的经济能力范围内的帮助下,去除完本地污染物。
