危急遮断器弹簧特性分析

吴宗健，杨晓锋，邱豪凯

（杭州中能汽轮动力有限公司，杭州310018）

0 引言

汽轮机是在高温、高压环境下作业的转动设备，其叶轮、叶片等在高转速工况下产生巨大的离心力，而其承受的应力中一大部分是由离心力引起的。设计过程中，转动部件通常只保留一定的强度余量，一旦转速超过其强度极限，便会造成叶片断裂、断轴等严重事故[1]。危急遮断器是在电子调速器跳闸失效后防止发生汽轮机飞车事故的唯一安全保护装置。

危急遮断器实际运行工况复杂，往往无法通过理论计算得出精确的跳闸转速。需要试验多次通过调整弹簧压缩量或者打磨销子长度来改变飞锤质量来获取目标跳闸转速。倪林森等[2]对某3 000 r/m in汽轮机设计机械式超速保护设备并进行试验验证，第一次试验时危急遮断器的动作转速比设计转速高130 r/m in，可通过调整弹簧压缩量来完成试验。

由此，本文研究了危急遮断器旋转时，弹簧的特性及对危急遮断器的跳闸转速对其产生的影响。

1 危急遮断器的工作原理

超速保护装置由危急遮断器和危急遮断油阀组成，危急遮断器是超速保护装置的转速感受机构，有飞锤式和飞环式2类，二者工作原理完全相同。飞锤式危急遮断器的基本结构如图1所示，主要构件有飞锤、销子、弹簧、导向套筒等。

图1 危急遮断器

1.1 飞锤计算公式和原理

飞锤为偏心设计，保证飞锤在离心力的作用下能沿导向套筒飞出。

飞锤离心力表示为[3]

式中：mc为飞锤＋销子的质量，kg；rc为飞锤＋销子的重心与转子中心的偏心距，mm；ω为角速度，rad/s。

飞锤位置A为汽轮机正常运行时，飞锤未动作时位置。此时飞锤受力分析如下：

式中：FCA为处于位置A 时飞锤的离心力，N；FαA为处于位置A 时弹簧对飞锤的作用力，N。

飞锤位置B为汽轮机转速超过动作转速，飞锤已经击出。此时飞锤受力分析如下

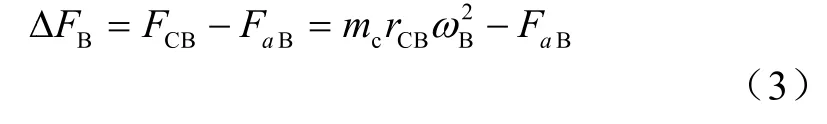
式中：FCB为处于位置B时飞锤的离心力，N；FαB为处于位置B时弹簧对飞锤的作用力，N。

当ΔFA＞0时飞锤开始动作，朝外击出。设计过程中要保证ΔFB＞0已保证击出过程中飞锤一直处于加速状态。

1.2 一般弹簧计算公式

这说明弹簧的应力与弹簧的线密度有关，应力是线密度函数，而且式（5）对于弹簧的非均匀伸长或局部伸长均适用[4]。

1.3 危急遮断器的弹簧计算公式

危急遮断器中弹簧模型可以简化为图2。a端为活动端，连接飞锤；b端为固定端；O处为旋转中心。弹簧为带预应力安装。

图2 弹簧本身旋转产生的离心力计算

弹簧在O处弹簧力

则弹簧的旋转中心O 处左右两侧的力平衡方程为

式中：FLa为左侧弹簧的离心力，N；FLb为右侧弹簧的离心力，N；Pa为左侧壁面对弹簧的作用力，N；Pb为右侧壁面对弹簧的作用力，N。

弹簧在变形过程中质量不变[4]，故满足

联立式（6）～式（8）可以求得Pa和Pb。

弹簧安装在危急遮断器内旋转时受离心力作用，在离心力作用下弹簧内部单元会发生复杂变形，同时引起弹簧左右两侧质量的变化。由此造成上述公式求解比较复杂，故下面采用Ansys数值计算的方式求解Pa和Pb。

2 危急遮断器的弹簧设计

2.1 方法1

将模型简化，将弹簧与飞锤作为一个整体计算偏心距与离心力[3]。弹簧对飞锤仅提供弹簧力fTA，没有考虑弹簧的离心力的作用。

2.2 方法2

考虑弹簧本身旋转所产生的离心力对二端的作用力的变化[5]，提出如下计算方法

由式（2）、式（4）、式（10）和式（11），可得计算公式

2.3 方法3

本文提出下列方法，采用Ansys的Static Structural 模块进行受力分析，提取弹簧的接触反力Pα。代入式（11）即可得到跳闸转速。

本模拟以飞锤未动作时，弹簧在旋转时受到自身离心力作用下克服弹簧力对两侧壁面的作用力。相当于弹簧两侧都为固定端，故对飞锤与叶轮之间采用绑定接触，简化分析问题。模拟分析的弹簧为安装状态，即弹簧已压缩至LA。网格模型见图3。

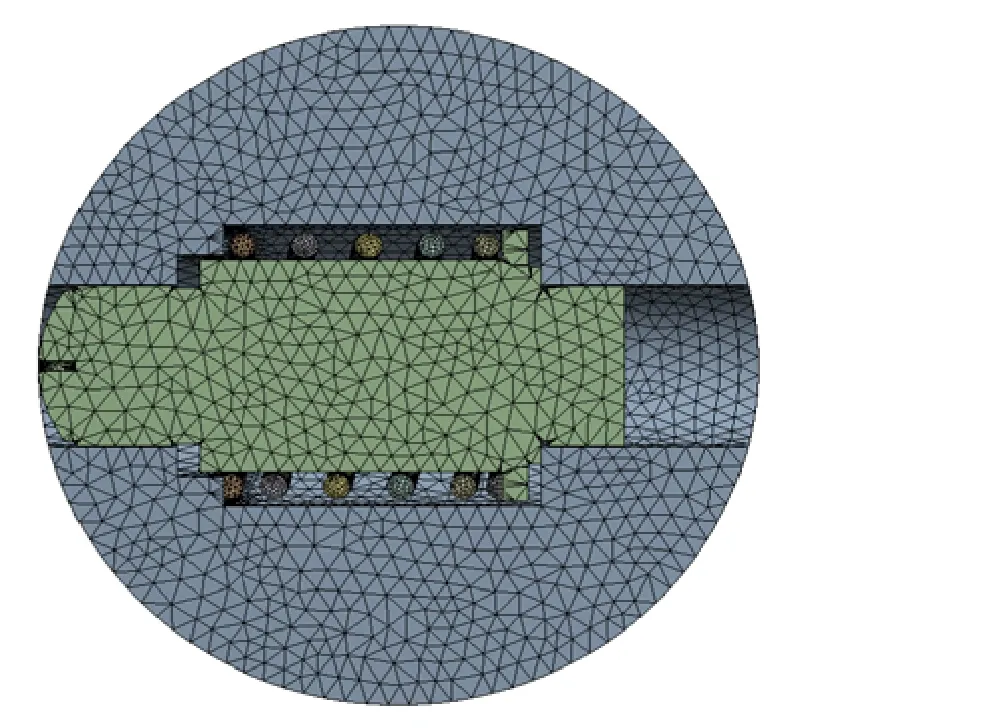
图3 网格模型

网络采用四面体绘制，对重点关注的弹簧和弹簧接触部分适当加密网格，以提高分析精度。分析的边界条件为叶轮绕中心旋转，转速设定为工作转速。叶轮壁面采用Frictionless Support。计算后提取接触反力Pa即可。参考式（2）、式（4）和式（11），可得计算公式

3 试验验证与方法比较

下列以1 500 r/min汽轮机的危急遮断器的弹簧为例，编写设计示例。为杜绝由弹簧加工误差引起的跳闸转速偏离，以下设计采用试验实测弹簧数据。

3.1 基本参数

经过详细设计确定当销子L＝45 mm 时飞锤基本参数，见表1。

表1 飞锤和弹簧测量数据

续表1 ：

3.2 计算结果

3.2.1方法1和方法2

将表1的数据代入式（9）、式（12）可分别得到方法1动作转速为ω＞169.28 rad/s、方法2动作转速ω＞164.72 rad/s。

3.2.2方法3

以工作转速为157 rad/s时，计算得到弹簧内部变形图，如图4所示。

图4 弹簧变形图

图4中的弹簧以O-O为旋转中心，弹簧左右2侧部分弹簧在离心力作用下压缩变形，靠近旋转中心线附近的弹簧在离心力作用下发生位移，左侧部分弹簧移动到右侧。从而证实了理论求解Pa和Pb的难度。

提取左右壁面接触反力可知弹簧离心力对飞锤的作用Pa＝6.65 N，弹簧离心力对轴固定端的作用力Pb＝26.836 N。参考式（1）可得弹簧离心力为FCL＝20.186 N。等式Pb-Pa=FCL成立，由此验证Ansys 计算弹簧离心力对飞锤的作用力Pa正确。

分别计算转速在157 rad/s～178 rad/s范围内的Pa值，得出转速与弹簧作用力关系，见图5。

图5 转速与弹簧作用力关系图

Pa与ω之间关系如下

由式（13）、式（14）可得ω＞163.47 rad/s。

3.2.3汽轮机跳闸试验

API Std 612中规定汽轮机出厂前要进行机械运转试验，故汽轮机试车时同时对本次设计的危急遮断器进行跳闸转速试验[6]。试验时，移除电子跳闸转速控制模块，通过控制系统控制汽轮机转速快速通过试验转速范围；而后，系统记录汽轮机跳闸转速即可。

按标准规定获得连续3次无趋向性跳闸值ω＞163.15 rad/s。

3.3 各方法结果比较

试验选取了不同销子长度，进行了汽轮机跳闸试验并获取了跳闸转速。为与计算结果单位统一，试验得到的跳闸转速单位为rad/s。

表2 试验跳闸转速和计算转速汇总

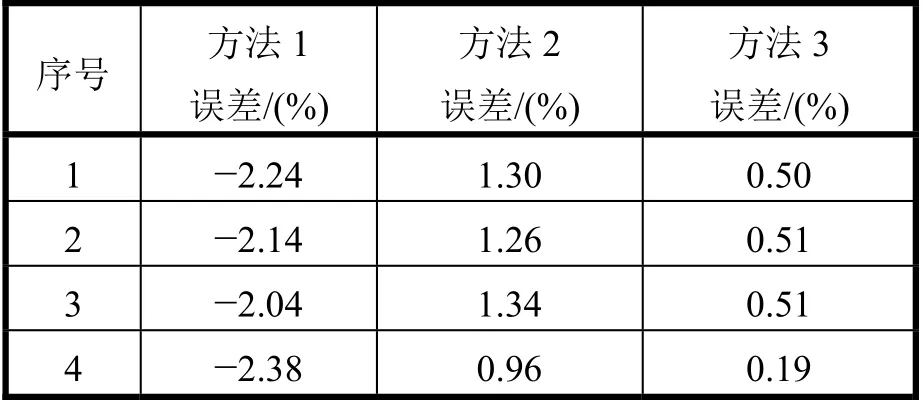
表3 各方法误差汇总

由表2和表3中可以清晰看出，本文计算结果与实际跳闸转速误差最小。API Std 612的条目16.3.3.2规定跳闸转速获得值应在正常跳闸转速设定值的1%以内[6]。

1）方法1误差的均方根平均值为−2.21%。文献提到在设计预变形量下，危急遮断器动作转速明显高于设计动作转速，并把原因归于弹簧刚度高于设计值[3]。本文认为其设计转速偏高的原因还包括把弹簧的离心力简单合并到飞锤的离心力中，造成误差偏大。

2）方法2误差的均方根平均值为1.23%。文献提出了一个简单的计算公式，但计算精度不满足标准要求[5]，实际使用仍需多次试验。

3）方法3误差的均方根平均值为0.45%。采用Ansys模拟计算弹簧在离心力作用下对飞锤的作用力，误差控制在标准要求的1%以内。通过本次危急遮断器跳闸试验可知，本方法满足设计要求，可以一次试验获得预设跳闸转速。

通过计算不同销子长度情况下的跳闸转速，得到了特定弹簧刚度、销子长度与跳闸转速的关系公式

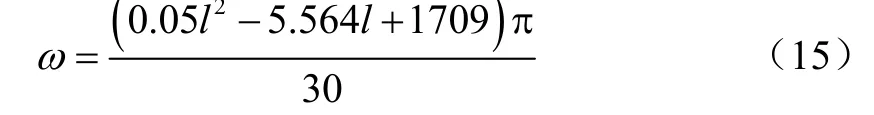
式中：l为销子长度，mm；ω为跳闸转速，rad/s。

危急遮断器属于汽轮机基础部件，通用性强，采用Ansys模拟计算得出Pa拟合公式。编写计算机程序，制造部门只需输入弹簧的质检数据和目标跳闸转速即可得到销子长度。以往制造部门为完成跳闸转速试验将花费1 h～2 h 并且多次试车，现在制造部门可以一次试车成功，节省了大量试车时间、试车蒸汽和人员配置等。本文研究内容的成功应用将为公司带来大量效益。

4 结论

1）危急遮断器的跳闸转速与弹簧力大小有关，因此弹簧力的计算是关键。

2）弹簧旋转时受到自身离心力作用，弹簧内部会发生位移变化，从而引起弹簧力的变化。

3）通过Ansys计算出精确的弹簧力，从而得出较为准确的跳闸转速。通过试验，验证了方法3误差的均方根平均值为0.45%，为后续实际使用提供了理论基础。

4）本文并未考虑摩擦力等因素对跳闸转速的影响，可以进一步研究如何提高跳闸转速的计算精度。