浮力摆波能发电装置的俘能特性分析

范梦雨，赵江滨，贾玉山，魏 渊，王建新

(1.武汉理工大学 能源与动力工程学院， 湖北 武汉 430063；2.国家水运安全技术研究中心可靠性工程研究所， 湖北 武汉 430063)

海洋能是一种可再生能源，分布广泛，能量密度高[1-2]，包括温差能、盐差能、潮汐能、海流能和波浪能，其中对波浪能的利用就占了海洋能的50%以上[3]。最近几年，许多国家诸如英国、美国、挪威、澳大利亚都在投资研究波浪能发电装置，这些装置的发展对于推进海洋能源的开发，波能的探索利用具有重大意义。目前波能利用发电技术也在逐渐成熟，出现了一批批的波能转换装置。浮力摆波能发电装置是其中一种。浮力摆波能发电装置的转动轴安装在海床附近，是一种近水面波能收集装置，其原型示意图见图1。摆板的运动是依靠波浪水质点的轨圆运动作用运动，依靠浮力大于重力复位，从而通过液压装置将波浪能吸收并转换为电能供利用。与其他波能转换装置相比，浮力摆式波能发电装置具有频率响应范围较宽、适应极端负载、低成本[4]等特点。国内外学者依据浮力摆的工作原理和优点对其进行了许多的研究工作。英国某公司制造了世界上发电功率最大的Oyster浮力摆式波能发电装置；浙江大学张大海[5-6]发明了一种浮力摆波能吸收装置，该装置以液压传动为基础，利用摆板的双行程运动吸收波浪能做功，并对影响摆板波能吸收的因素(摆板形状)和液压传动做功系统的运行机理进行了研究；李雪临[7]等通过分析摆板的质量、质量分布、结构等参数对浮力摆的水动力性能进行了研究；芬兰的AW-Energy公司研制了水下浸没工作方式的WaveRoller装置[8]，并随后进行了样机海试试验，规格为3 m×1.8 m的浮力摆在水深10～15 m处，单机获得了较高的发电功率，达13 kW；哈尔滨工程大学的袁正[4]通过CFD软件分析了阻尼、波高、波频等参数对浮力摆波能发电装置的影响。

图1 浮力摆波能发电装置原型示意图

1 浮力摆波能发电装置

1.1 装置简介

浮力摆波能发电装置系统是由3部分组成，分别是摆板部分、液压缸部分和底座部分。浮力摆波能发电装置的浮力摆结构示意图如图2所示，浮筒长度为7 m，浮筒直径为0.92 m，两浮筒之间轴间距为1.02 m，浮力摆的总高度为5 m。

图2 浮力摆结构示意图

1.2 装置能量转化

浮力摆波能发电装置是通过底座部分直接铰接在海床上，其波能吸收转换是通过二级能量转换过程来实现的。浮力摆受到波浪的冲击和净浮力作用驱动摆板绕着转动轴往复摆动，驱动液压缸往复运动，从而将波浪能转化为液压缸的液压能，再将液压能输送到水力发电机中，由水力发电机转换为电能以供用户使用，能量转换流程为波浪能通过浮力摆的摆动转化为液压缸的液压能，液压能通过液压马达和发电机转化为电能。

2 浮力摆数值模型

采用以势流理论为基础ANSYS-AQWA仿真软件[9]实施模拟，软件以边界元方法为算法求解计算，软件的频域计算结果传递给时域以进行时域计算，从而求得物体在波浪中的受力和运动响应。

2.1 数学模型

浮力摆波能发电装置可以安装在浅水区域发电供附近居民用电。浮力摆在海水中受波浪力摆动做功，依靠浮力提供恢复力回复正位。在海浪环境中，当装置的运动频率与波浪的频率相同时即发生共振，最佳阻尼下的波能发电效率理论上将会达到1[10]。故在浮力摆摆动过程中，使摆板固有频率和波浪频率相同，可最大化浮力摆的发电能力，因此对浮力摆波能发电装置建立运动模型。本文采用机械振动理论，考虑浮力摆的附加转动惯量，推导净浮力对浮力摆波能发电装置运动影响的方程，分析净浮力对装置俘能特性的影响；研究浮力摆的铰接位置以及阻尼系数对装置运动和发电的影响；为浮力摆波能发电装置的优化和装置的实际应用提供参考依据。

装置的运动数学模型：

(1)

装置固有频率可表示为：

(2)

k可表达为:

(3)

浮力摆做小角度运动，M简化表示为：

(4)

当谐振条件满足时，浮力摆的固有频率等于波浪的圆频率，即ωn=ω0，此时浮力摆波能发电装置的发电能力理论上达到最大值。

2.2 摆板建模和网格划分

去掉底座部分，液压部分简化为线性阻尼,将模型简化仿真。使用SOLIDWORKS软件绘制三维体模型，导入AQWA中的Design Modeler中，全局坐标系xy轴在水线面上，z轴与xy平面垂直，坐标系的原点在水线面形心处(最下端浮筒的轴线上)，浮力摆的竖直方向与z轴平行。由于AQWA仅是针对面体和线体进行计算，将浮力摆体模型转换为面模型，并沿z轴向下移动，露出水面高度为0.46 m，利用水线面划分模型为上下两部分。之后在mesh模块实施表面网格划分，浮力摆三维模型和网格划分如图3所示。

图3 浮力摆三维模型和网格划分

3 发电效率计算

波能发电装置对波能捕获的品质主要是通过一级转换效率来衡量的。浮力摆在海水中往复运动对波能吸收的一级转换效率由浮力摆吸收的功率和波浪功率密度与摆宽的乘积决定，而浮力摆吸收的功率Pb可由式(5)计算。

(5)

本文研究的波浪环境为随机波，浮力摆一级波能吸收的转换效率η和在一定水深条件下的波浪功率密度I可以按式(6)、式(7)计算。

(6)

(7)

式中，B为浮筒的长度，m；Hs为有义波高，m；Te为随机波平均上跨周期(Te=m-1/m0，其中m-1为波浪谱-1阶矩，m0为波浪谱0阶矩)，s；g为重力加速度，m/s2；κ为波数，m-1；h为水深，m；ρ为海水密度，kg/m3。

4 数值模拟与结果分析

由于波浪是波浪水质点由于风力和重力的作用而形成的，且波浪运动具有随机性，真实的海浪环境不能仅靠规则波来描述，本文研究的波浪环境为接近于海洋的真实环境，在使用软件仿真时采用单向的不规则波，选取不规则波JONSWAP谱为入射波浪谱，有义波高为1 m，平均上跨周期为4.7 s，计算得到的波浪功率密度为2.77 kW/m，浮力摆的放置水深为12 m，摆板静止时露出水面高度为0.46 m，仿真的时长设置为1 800 s。本文按浮力摆所受到的净浮力、阻尼系数、转动轴铰接位置等进行计算并分析。

4.1 净浮力对俘能特性的影响

设置9种工况进行对比分析，分别是净浮力为装置静止时浮力的399/400，199/200，99/100，49/50，46/50，36/50，26/50，16/50，6/50，阻尼系数设置为1.327×105N·m·rad/s,图4为波能一级转换效率和平均吸收功率随净浮力增加的变化趋势(图4中横坐标为净浮力和装置静止时浮力的比值，记作R，为清楚地观察在较大净浮力时的变化情况，采用等距横坐标)，由图4可知，随着R的增加，浮力摆的平均吸收功率和一级转换效率逐渐增大，最后趋于平稳。由式(5)、式(6)可知，装置的一级转换效率与角速度相关，随着净浮力的增大，摆板的重力逐渐减小，质量减小，使得转动惯量和附加转动惯量减小，固有周期随着增大。表1为装置随着净浮力增大的固有周期变化情况，在R=0.92时，装置的固有周期接近随机波的平均上跨周期4.7 s，使得装置运动响应增大，转换效率达到平稳的初始点；虽然固有周期一直在增加，但转动惯量逐渐减小，回复力矩逐渐增大，运动响应较大，这可能是转换效率最终在R≥0.92后平稳的原因。从图4中还可以知道，净浮力较大，转换效率就较高，理论上R≥0.92时，对装置的波能转换效率较为有益，但是净浮力越大，摆板受重力越小，厚度就越小，抵抗风浪冲击的结构强度就越差。在实际应用中考虑装置可靠性，结构强度至关重要，所以说净浮力并非越大越好，在R=0.92和R=0.98间转换效率相差不大，海试试验选择R=0.92较佳。当摆板的净浮力为浮力的26/50时，此时质量为11.7 t(R=0.52)，平均吸收功率为2.44 kW，一级转换效率为12.58%，和文献[7]计算结果基本一致，误差0.07%，保证计算结果的可靠性。

图4 一级转换效率和平均吸收功率随R的变化趋势

表1 浮力摆固有周期变化

4.2 阻尼系数对俘能特性的影响

阻尼系数是表征阻尼的关键参数，因此改变装置阻尼系数，装置的平均吸收功率和一级转换效率也不同。本文将阻尼系数每增加1×105设置，分别是1.327×105，2.327×105，3.327×105，4.327×105，5.327×105，6.327×105，7.327×105，8.327×105。摆板重力设置为浮力的24/50，铰接位置到摆板质心的距离为总高度的50%。通过改变阻尼系数对装置俘能特性的影响如图5所示，一级转换效率和平均吸收功率随阻尼系数的增加先增大后减小，从图5知，装置运动存在最佳阻尼系数，使一级转换效率和平均吸收功率达到最大，此时的最佳阻尼系数为4.327×105，浮力对波能的平均吸收功率为3.99 kW，一级转换效率为20.58 %。装置一级转换效率和平均吸收功率之所以先增大后减小是因为阻尼系数在逐渐增加，浮力摆运动中受阻尼力矩也逐渐增加，角速度逐渐减小，但在阻尼系数增加到最佳阻尼系数之前，浮力摆运动角速度虽然是在减小的，但相对来说仍较大；在阻尼系数超过最佳阻尼系数继续增加时，角速度虽逐渐增大其角速度相对来说是较小的。可以通过摆角范围的变化观察运动响应随阻尼的变化情况，摆角范围如表2所示。另外从图5可以看出，在最佳阻尼系数之前，随着阻尼系数的减小，一级波能转换效率降低较迅速，在最佳阻尼系数之后，一级波能转换效率降低较为平缓，也就是说阻尼系数稍大对装置的一级转换效率是有益的。

图5 一级转换效率和平均吸收功率的变化趋势

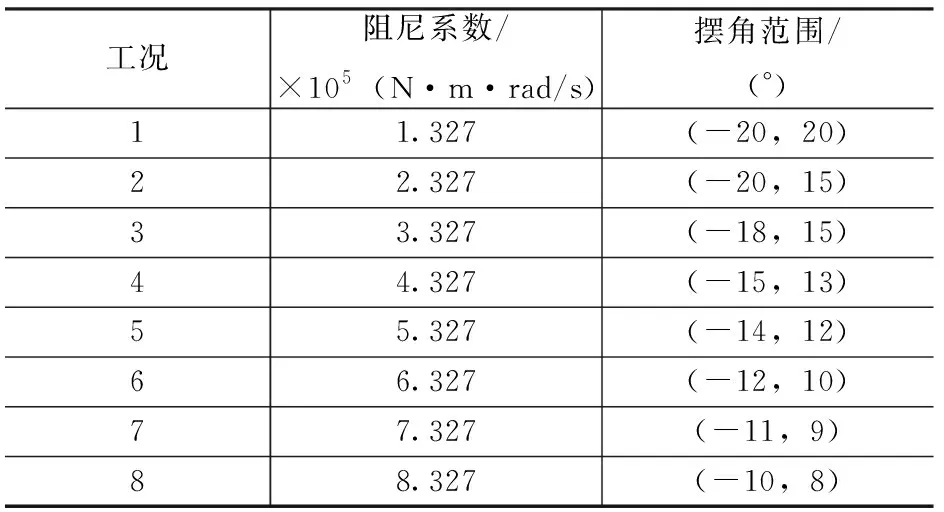
表2 摆角范围

4.3 铰接位置对俘能特性的影响

在研究过程中发现浮力摆铰接位置对俘能特性有较大影响。摆板质量设为11.7 t，装置一级转换效率和平均吸收功率随Q的变化结果如图6所示，图6中横坐标为摆板铰接位置到质心的距离占总高度的百分比(Q)，从图6可知，一级转换效率和装置平均吸收功率随Q的增大先增大后减小，存在最佳的铰接位置，最佳的位置在Q=29.2%处，在摆板最下端上部1 m位置处，此时的平均吸收功率为3.31 kW，一级波能转换效率为17.07%。从图6还可知，当Q≥29.2%时，一级转换效率降低速率没有增加时的快，可见Q稍微大的阶段对俘获能量是有益的。浮力摆的一级转换效率之所以出现先增大后减小的情况，是因为随着铰接位置向下移动，摆板受到波浪力矩先增大后减小，且转动轴在Q=29.2%的位置时，波浪力矩最大，同时转动轴在Q=29.2%的位置时，角速度出现峰值，这致使摆板运动角速度呈现先增加后减小的趋势。通过观察摆板随着铰接位置改变的平均波浪力矩的变化，了解浮力摆在运动中的受力，图7为摆板受到的平均波浪力矩随Q的变化趋势。

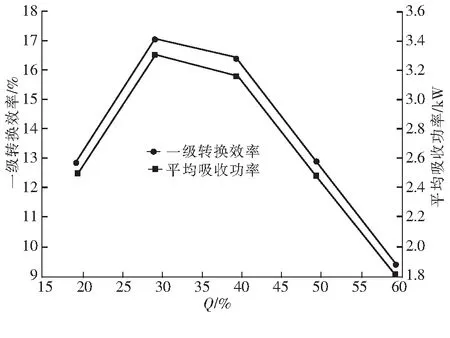
图6 一级转换效率和平均吸收功率随Q的变化结果

图7 平均波浪力矩随Q的变化趋势

5 结束语

本文利用AQWA水动力学分析软件将浮力摆波能转换装置系统进行了简化，并对摆板建立时域数值模型。分析了净浮力、阻尼系数和铰接位置对浮力摆俘能特性的影响，结果如下。

1)净浮力的变化会较大地影响转换效率，净浮力越大转换效率也越高，并最终趋于平稳。

2)随着阻尼系数的增加，转换效率先增大后减小，且存在最佳阻尼系数。

3)一级转换效率和平均吸收功率随着铰接位置的纵向向下移动先增加后减小，存在最佳的铰接位置使俘获功率、转换效率达到峰值。

本文是简化建模进行仿真计算，计算结果会有一定的偏差，后续的研究中应进行全模型数值建模计算，并通过试验进行验证，得到更加准确的计算结果。