基于IDRISI降雨量的时间序列分析与预测

申晓哲，关 霄，牛毓君

(1.山西省造林局，山西 太原 030012； 2.山西省煤炭地质资源环境调查院，山西 太原 030006)

降雨是反映一个地区气候状况的重要指标，它与社会的发展息息相关，而且影响人类生存。降雨量是衡量干旱程度的一个重要指标，降雨量的大小直接影响林业生产。笔者以全球降雨量为研究对象，进行了空间尺度和时间尺度上的分析，并运用模型对降雨量做出科学预测。由此，可以根据降雨量变化来选择适宜生长的树种，提高树种的成活率和保存率。

1 研究方法

1.1 降雨量分析

以全球1982年至2000年5月、6月、9月的ETM降雨量数据作为研究对象，运用图像比对、图像相减和回归分析的方法绘制降雨量差值趋势图，分别对空间尺度(不同年份、不同月份)和时间尺度(不同年份同一月份)的降雨差异性进行分析。由于本文所使用的ETM数据存在误差以及数据缺失，通过缺失数据插值、数据降噪、消除季节性影响等方法对所使用的数据进行预处理。

1.2 降雨量预测

运用IDRISI中的全球趋势模型(Earth Trend Modeler)对未来降雨量进行预测，分别进行小波分析、序列趋势分析、STA分析、EOT，PCA，线性建模分析等，对在时间序列上降雨量的特征和趋势做出判断和分析。

2 全球降雨量的差值分析

2.1 空间尺度上的降雨量分析

1982年至2000年5月和6月的降雨量差值趋势图见图1.

图1 5月和6月间降雨量差值趋势图

由图1可以看出，不同年份5月与6月的降雨量差值虽不尽相同，但其总体趋势是一致的。1982年至2000年，5月和6月的降雨量差值基本保持不变，且稍有增加。表明在这20年中未发生非人为或人为的降雨量变化，但差值的增长与不同年份的降雨量以及全年气候变化有关。此外，相邻年份5月和6月降雨量差值的变化基本保持在0.05左右，这对未来在无特殊人为或自然破坏的情况下进行降雨量预测具有实际作用。

1982年至2000年6月和9月间的降雨量差值趋势图见图2.

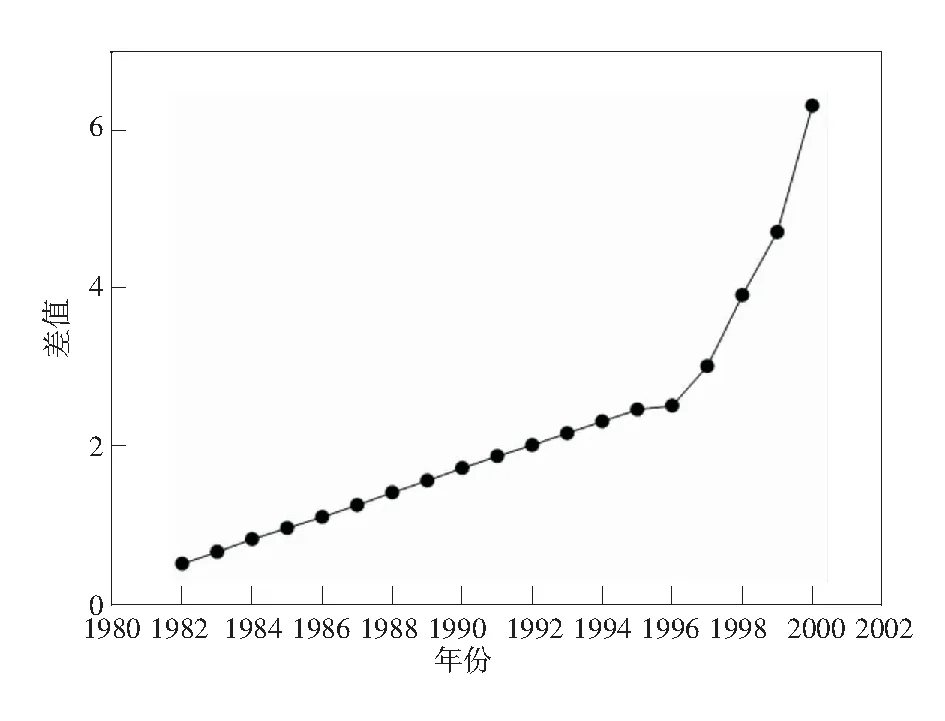
图2 6月和9月间降雨量差值趋势图

由图2可以发现，与5月和6月降雨量差值趋势图不同，6月和9月间降雨量差值趋势图不是很平缓。1982年至2000年，6月和9月间降雨量差值增加较为明显，但增长幅度有所不同，1982年至1996年间增长幅度基本相同，而1996年至2000年间增长迅速，这可能与此期间的气候变化有关。但由于在5月和6月降雨量差值趋势图中未发现异常，这种异常的出现可能是因为9月份降雨迅速增加引起的。从图2中可以看出，6月和9月间的降雨差值持续增长，但该增长趋势不满足任何规律，可以作为未来降雨量简单预测的依据，不可作为预测的标准。特别是由于全球气候变化或是特殊自然条件的影响，该趋势不能作为预测模型。

2.2 时间尺度上的降雨量分析

以6月份全球降雨量为例，计算前后2年的降雨量差值，得出1982年至2000年6月降雨量差值趋势图，见图3.

图3 1982年至2000年6月降雨量差值趋势图

由图3可以发现，1982年至2000年6月的降雨量差值趋势图曲线类似于正弦波，出现很强的周期性。6月份降雨量差值基本保持不变，且年际差异大致等于-0.02.这说明在20年中6月份降雨量持续走低，降雨普遍减少，可以依据该数据对未来在无特殊人为或自然破坏情况下的降雨量进行预测。在做图像相减差异时，1991年至1992年图像相减差值出现无取值的情况，1998年至1999年年际差异接近-0.10，超出差值允许范围，予以剔除。

3 全球趋势模型预测降雨量

笔者运用IDRISI中的全球趋势模型(Earth Trend Modeler)对未来降雨量进行预测，分别进行小波分析、序列趋势分析、STA分析、EOT，PCA，线性建模分析等。由于在上述分析的6月份降雨量与正弦函数附和性较好，故而以此模型进行预测，得到全球6月份降雨量的预测公式为：

式中：T——年份。

根据公式预测2000年至2007年全球6月份的降雨量，并与实际降水量数据进行对比，结果见图4.

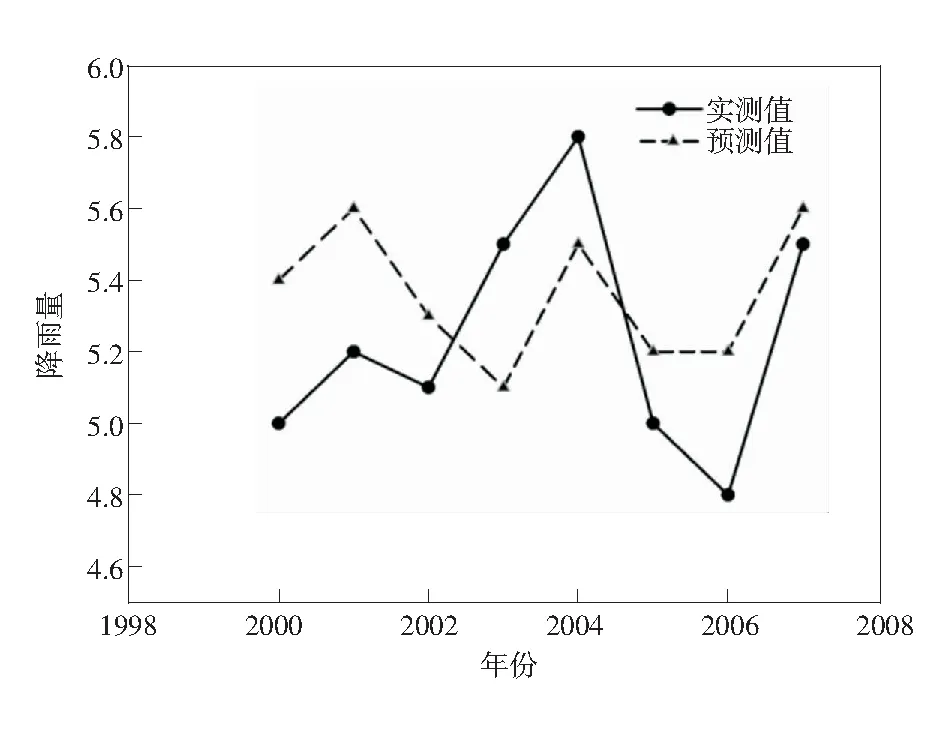
图4 2000年至2007年全球6月降雨量实测值与预测值

由图4可以看出，降雨量预测数据与实际数据差异不大且变化趋势相似，因此，全球趋势模型的建立相对可靠、科学。

4 结论与讨论

1) 笔者通过时间尺度和空间尺度对全球1982年至2000年5月、6月、9月的降雨数据进行定量分析。结果表明，1982年至2000年，全球这3个月降雨量普遍增加，但增量不大；5月和6月的降雨量差值在长时间序列上基本保持稳定，验证了这20年雨季未发生非自然条件的降雨变化；通过分析6月和9月间的降雨量差值，发现9月份的降雨量在时间序列上明显增加，这可能成为验证冬季降雨增多的证据。