基于最大相关熵的雷达扩展卡尔曼滤波算法研究

王恒，李春霞，刘守训

(1.中国传媒大学 信息与通信工程学院，北京100024；2.中国电子科技集团公司 信息科学研究院，北京 10081)

1 引言

在实际生活中，雷达目标跟踪在民用、军事等诸多领域都有十分重要的应用。在雷达跟踪系统中，由于目标状态以及量测信息一般是在不同坐标系下获得的，这使得系统滤波模型是非线性的[1]。对于非线性滤波问题，通常的处理方法是运用线性化技巧将非线性滤波问题近似为线性滤波[2]，最常用的滤波算法有扩展卡尔曼滤波(EKF)[3]、不敏卡尔曼滤波(UKF)[4]、转换量测卡尔曼滤波(CMKF)[5].但这些滤波算法前提要求是系统量测噪声为高斯噪声。然而，雷达系统中的量测噪声往往并不是高斯噪声而是重尾非高斯噪声，这就导致应用传统算法对目标进行跟踪时性能急剧下降，跟踪精度大大降低。

针对非高斯噪声下的目标跟踪问题，一些算法不断被提出。例如，粒子滤波(PF)算法是近年来兴起的一种非线性滤波算法，该方法不受高斯噪声假设的限定，适用于任何情况下的量测模型[6]；基于学生t分布的鲁棒滤波算法，用来解决过程噪声和量测噪声均是重尾噪声下的非线性状态问题[7]；近年来，信息论学习中的优化准则受到了越来越多的关注，它直接使用从数据估计的信息论量(如熵)代替通常的二阶统计量(如方差、协方差)作为优化代价[8-12]。最大相关熵准则(MCC)便属于信息论学习领域，其优势在于不但可以获得误差的二阶项信息，还可以捕捉滤波误差的高阶统计量，从而使得系统跟踪性能得到极大改善，提高系统鲁棒性。相比于最小均方误差优化准则(MMSE)，该准则不受高斯分布假设，尤其在误差分布有离群值、非零均值时展现出强大的优越性[13]。

文献[14]中提出了线性最大相关熵扩展卡尔曼滤波(LRMCEKF)和非线性最大相关熵扩展卡尔曼滤波(NRMCEKF)，用来解决状态方程和量测方程均为非线性且量测噪声为重尾噪声的滤波问题。本文将最大相关熵扩展卡尔曼滤波(MCEKF)应用到雷达跟踪系统中。该算法中，状态和协方差矩阵的先验估计与传统扩展卡尔曼(EKF)滤波算法状态与协方差一步预测相同，而后验估计则通过定点迭代过程进行更新[15]。

2 问题描述

对目标进行跟踪，首先需要建立目标运动的状态方程以及量测方程。对于雷达来说，目标的状态信息通常是在直角坐标系下获得的，而量测信息则是在极坐标系下获得的，这就导致雷达目标跟踪系统是非线性的。

考虑到现实中目标大多是做匀速直线运动，所以雷达直角坐标系下离散状态方程为，

X(k+1)=F(k)X(k)+G(k)v(k)

(1)

雷达极坐标系下离散时间系统的量测方程为，

重尾噪声往往存在于雷达量测以及GPS定位系统中。重尾噪声与高斯噪声的区别主要是重尾噪声尾部较长，而中心类似高斯形状。重尾噪声可以分解为高斯噪声和具有“厚尾”特性噪声的加权和。这些“厚尾噪声”有t分布、拉普拉斯分布以及大方差的高斯分布[17]。所以本文采用不同方差的高斯混合噪声对雷达非高斯噪声进行建模。混合高斯噪声模型可以表示为，

f(k)～(1-ϑ)N(μ1，P1)+ϑN(μ2，P2)

(3)

其中，0≤ϑ<1 代表重尾噪声的强弱，N(μ1，P1)代表均值为μ1方差为P1的正常高斯噪声，N(μ2，P2)代表大方差的高斯噪声[18]。

3 基于最大相关熵的扩展卡尔曼滤波

扩展卡尔曼滤波(EKF)是处理非线性跟踪系统的一个重要工具，基本思想是利用泰勒级数将非线性滤波问题近似为线性滤波问题，其优势在于算法简单，计算量小[19]。基于最大相关熵的扩展卡尔曼滤波(MCEKF)的滤波过程为，

(2)预测。根据式(4)和(5)得到状态和协方差的先验更新。然后根据式(6)和式(8)得到量测先验更新值及其雅克比矩阵。

(4)

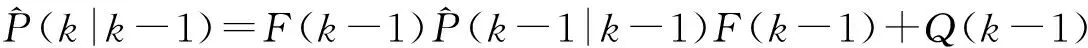
(5)

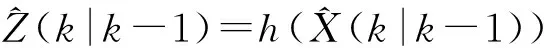
(6)

(7)

(3)结合EKF非线性模型，可以得到非线性回归模型[14]，

(8)

其中，

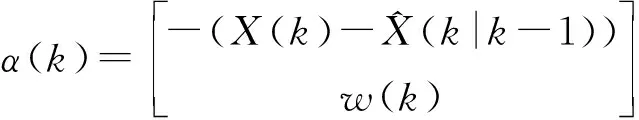
(9)

α(k)的协方差矩阵可以表示为，

=M(k)MT(k)

(10)

其中，M(k)是对协方差矩阵E[α(k)α(k)T] 进行Cholesky分解得到的结果。将式(8)两边分别左乘M-1(k)，可以得到，

D(k)=B(X(k))+e(k)

(11)

(4)为了防止量测异常引起的C(k)奇异，用以下方法来解决。

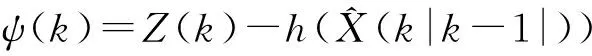
(12)

(13)

β(k)=ψT(k)η-1(k)ψ(k)

(14)

(6)迭代过程。

(15)

(16)

(17)

其中，Gσ(·)为高斯核函数，σ表示核带宽，

(18)

(19)

(20)

(21)

(22)

比较当前迭代步的估计以及上一步的迭代估计，如果满足，

(23)

(7)k=k+1重复步骤(2)到步骤(6)直至滤波结束。

4 仿真实验

假设雷达位于坐标原点，目标的初始位置设为(200km，400km)，目标的初始速度为(220m/s，-180m/s)，采样点数为N=100，采样间隔 T=1s，混合高斯噪声中大方差高斯噪声的方差是正常高斯噪声的104倍，蒙特卡罗仿真次数为M=100。在仿真过程中，滤波的初始值由两点法给出。本文分别应用EKF算法与MCEKF算法对目标进行跟踪。

图1和图2分别为非线性高斯系统中传统EKF算法与MCEKF算法位置以及速度均方根误差结果对比图。从均方根误差滤波结果可以看出，当量测噪声为高斯噪声假设时，滤波位置均方根误差大约在40m，而速度均方根误差大约在3.8m/s左右，MCEKF滤波效果与传统的EKF滤波精确度以及鲁棒性近似相同，都能实现很好的跟踪，且传统的EKF滤波效果略好于MCEKF。

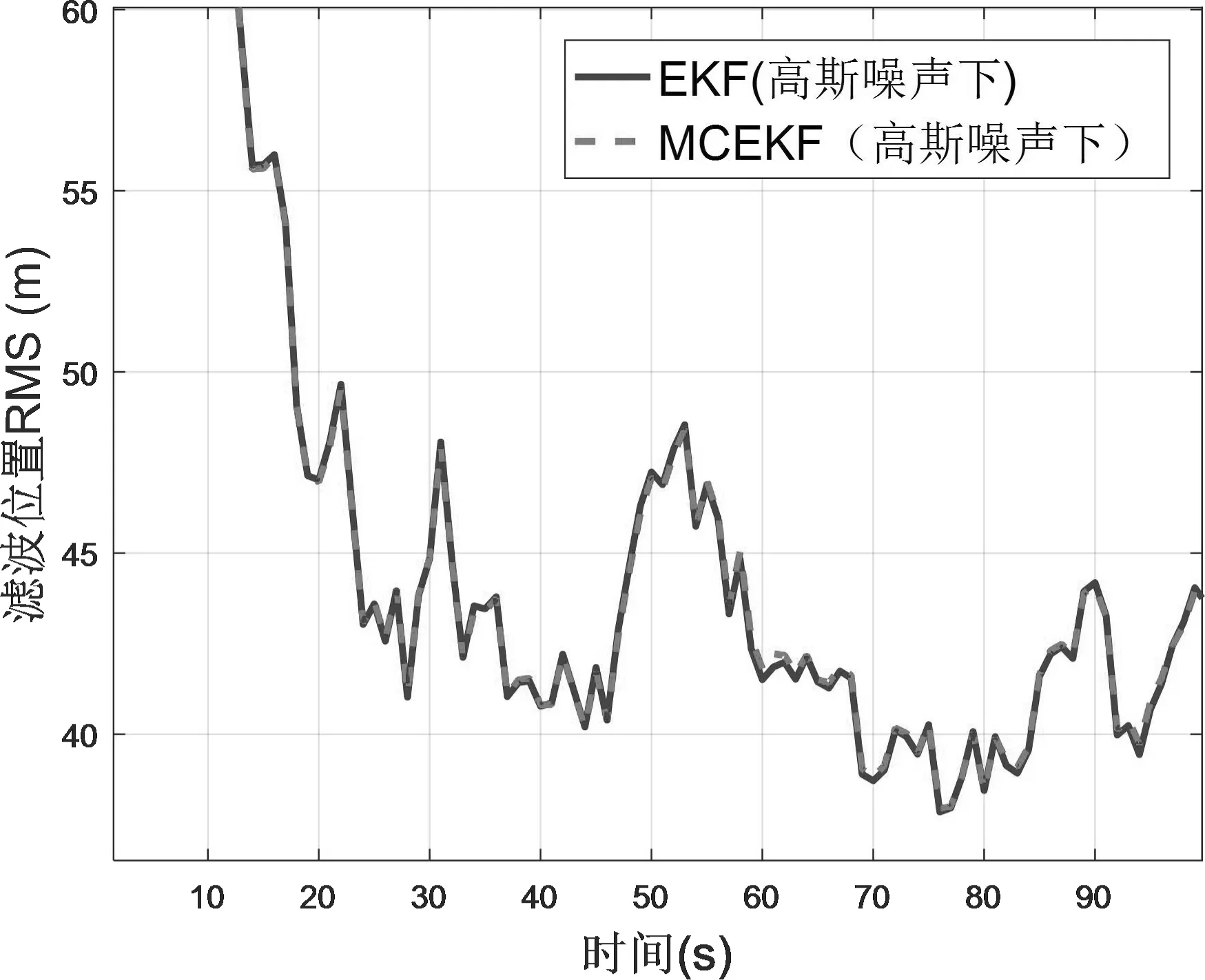
图1 高斯噪声下EKF与MCEKF位置均方根误差对比

图2 高斯噪声下EKF与MCEKF速度均方根误差对比

图3和图4分别为非线性非高斯系统中传统EKF算法与MCEKF算法位置以及速度均方根误差结果对比图。结果显示，当量测噪声为非高斯噪声时，滤波位置均方根误差上升到300m，上升了260m左右；速度均方根误差上升到10m/s，上升了6.2m/s左右，可见传统滤波算法中当量测噪声为非高斯噪声时，跟踪性能出现明显恶化，目标跟踪性能严重下降。从滤波效果对比来看，MCEKF滤波效果明显优于传统的EKF滤波效果，MCEKF算法的滤波精度更高，鲁棒性更强。

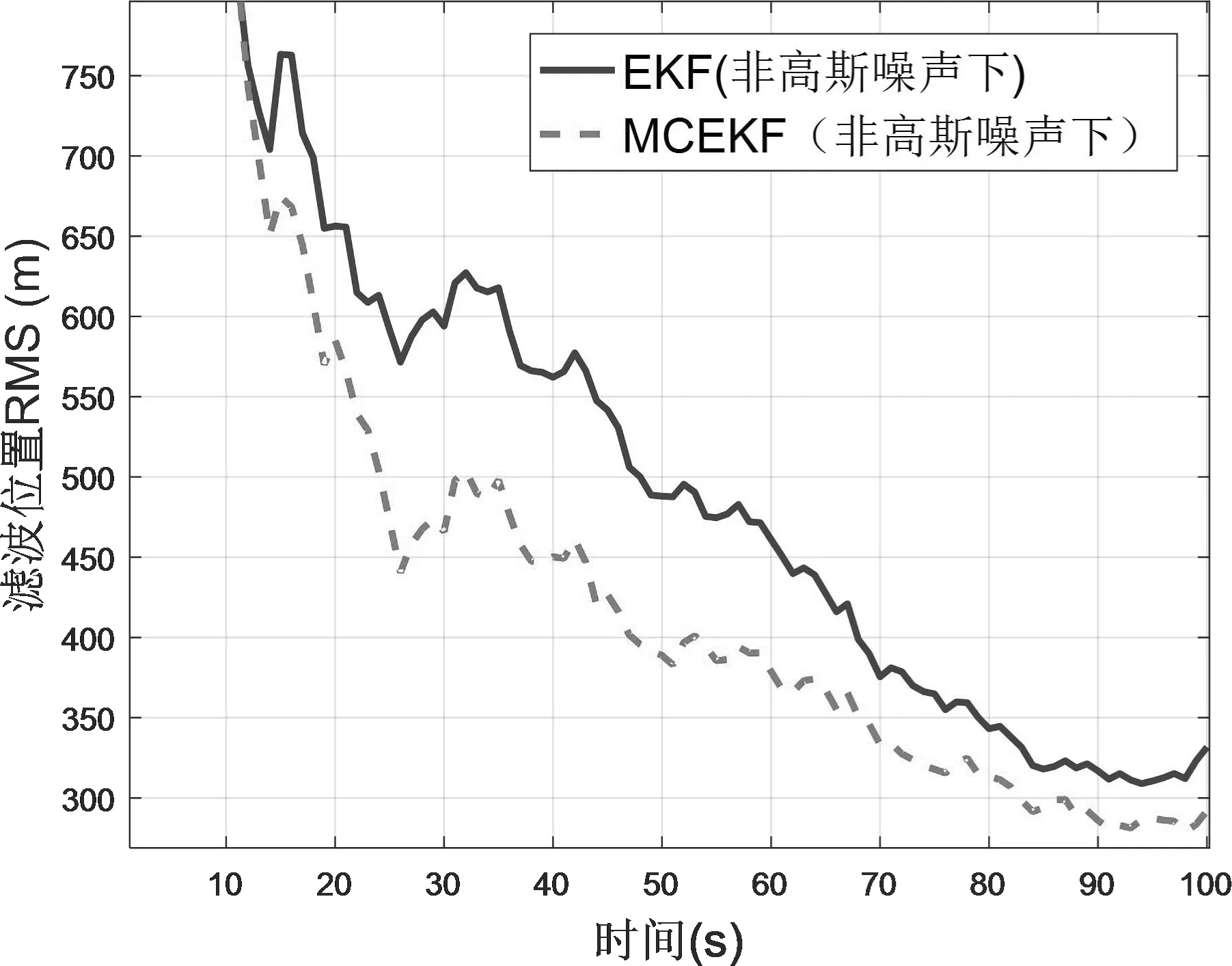
图3 非斯噪声下EKF与MCEKF位置均方根误差对比

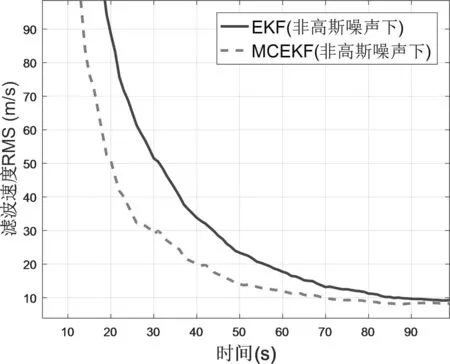
图4 非斯噪声下EKF与MCEKF位置均方根误差对比

5 结束语

在本文中，我们将最大相关熵引入到雷达跟踪系统中，当系统跟踪模型为非线性且量测噪声为非高斯噪声时，传统滤波算法无法保证系统的跟踪性能，出现恶化及鲁棒性降低的现象，这是由于传统算法均是在高斯假设下进行滤波的。而最大相关熵扩展卡尔曼滤波是基于MCC而非传统的MMSE作为优化准则，相较传统算法只能保留误差二阶矩，该准则可以保留跟踪误差的更高阶信息，提高算法的鲁棒性。在仿真实验中，比较了EKF与MCEKF在不同量测噪声下跟踪性能的差异，结果表明，MCEKF在非线性非高斯情况下跟踪效果明显好于EKF的跟踪效果，该算法不仅能解决非线性跟踪问题同时可以有效抑制非高斯噪声的干扰，提高雷达跟踪精度。