基于牛顿插值的抗差卡尔曼滤波算法

蔡保杰，邵 雷，李佳伟，李正杰

（1.空军工程大学 防空反导学院，西安 710051；2.西安电子科技大学 电子工程学院，西安 710071）

0 引言

导航系统在航空航天和日常生活中应用广泛。导航的方法有很多种，惯性导航和卫星导航的组合导航的方法是最为常用的1 种[1]。在运载体运动过程中，由于所处环境错综复杂，卫星导航的观测值会出现损坏的情况，严重影响导航的精度。

对于观测值故障问题[2-3]，常用的是传统抗差卡尔曼（Kalman）滤波方法[4]，文献[5]中构造了1 个故障检验公式，与设定的卡方检验阈值相比较，对检验值进行分段处理。文献[6]先用假设检验的方法检测出故障观测值的具体位置，用设定的门限值代替观测噪声值，可以较大程度地减小粗差的影响。文献[7]在一步预测均方误差阵上乘1 个渐消因子，进行自适应滤波。文献[8]通过降低滤波增益值来达到修正预测值的效果。文献[9]提出错误预警率和故障探测率的概念，对故障的定位更加精确。文献[10]通过等价权函数法对观测噪 声方差阵进行替换，可以实时有效地滤除粗差。

上述方法都能一定程度地减小粗差带来的影响，但也存在不足之处。卡方检验并不能保证百分之百的正确率，适当地选取阈值尤为重要。当检测系统出现误检情况时，用门限值代替正确的观测值也会造成观测值误差相对增大。针对这种情况，本文提出1 种基于卡方检验和牛顿插值的抗差滤波方法，利用前几个时刻的观测值组成的牛顿插值多项式进行外延，对当前时刻的故障观测值进行替换，以使组合导航系统稳定性更高，抗差能力更强。

1 组合导航系统建模与常用的抗差滤波方法概述

1.1 组合导航系统建模

导航系统能够测量并解算出运载体的瞬时运动状态和位置，提供给驾驶员或自动驾驶仪，以实现对运载体的正确操纵或控制。随着科学技术的发展，可供导航系统利用的信息源越来越多，导航系统种类也越来越多。捷联惯导(strapdown inertial navigation system， SINS)和全球卫星导航系统(global navigation satellite system， GNSS)所构成的组合导航是近年来导航领域最常使用的1 种方法，SINS 作为主导航系统，利用惯性器件实时解算出运载体的位置、速度等信息，而GNSS 也可以对SINS 不断地进行修正，避免了捷联惯导系统误差随时间增大的问题。

SINS/GNSS 的组合方式有松组合[11-13]、紧组合、深组合等。松组合的状态量为

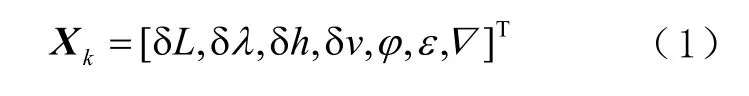
式中： δL 为经度误差； δλ 为纬度误差； δ h为高度误 差；δ v = [ δ vx， δ vy， δvz]为 速度误差；φ =[φx，φy，φz]为 姿 态 角 误 差； ε=[εx， εy，εz]为 陀 螺 仪 漂 移 误 差∇=[∇x，∇y，∇z]为 加 速 度 计 零 偏 误 差。其 状 态 方 程离散化后的形式为

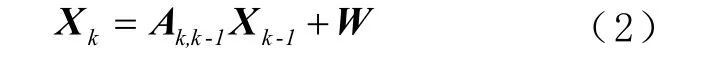
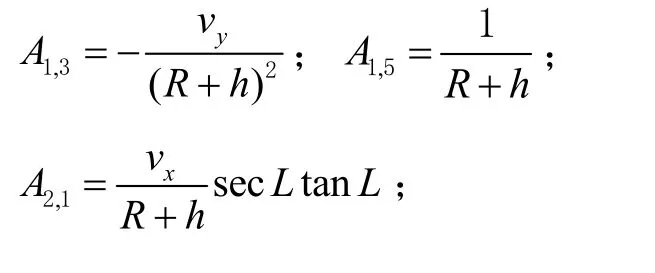
式中： Ak,k-1为状态转移矩阵；W 为系统噪声。当状态向量为15 维时， Ak,k-1是1 个15 维的方阵，其非零项为： 其中：ωie为地球自转角速度；fx、fy、fz为加速度计测得的比力信息；R 为地球半径。SINS/GNSS 的观测模型取GNSS 和SINS 输出的位置和速度之差作为 观 测 值，观 测 向 量 为 Zk= [rGNSS- rSINS，vGNSS-vSINS]T。其中： r =[ L， λ， h]； v =[ vx， vy， vz]。

量测方程为

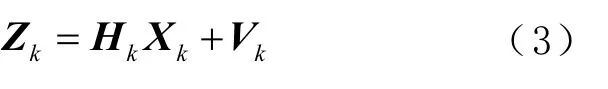
式中： Hk为量测矩阵；Vk为量测噪声。 Hk为1 个6 行15 列的矩阵，其非零元素为： H1，2=R cos L ;H2，1=R; H4，4=1; H5，5=1; H6，6=1。

1.2 2 种常用的抗差滤波方法

1.2.1 等价权函数法

等价权函数法[9,14]为调整观测噪声协方差矩阵 kR 的大小，抗差卡尔曼滤波在第k 时刻的估计值可以表示为

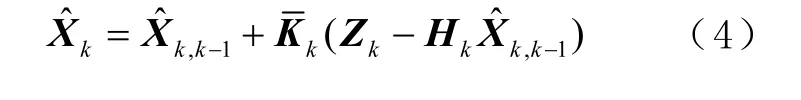
而式（4）中滤波增益为

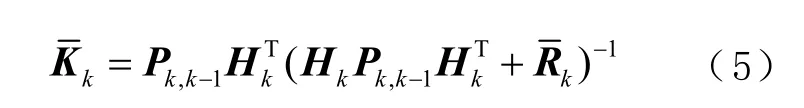
式中： Pk，k-1为一步预测均方误差阵；Rk为 Rk的等价权矩阵，而Rk可以通过丹麦法、胡贝尔（Huber）函数或通过中国科学院测量与地球物理研究所(Institute of Geodesy & Geophysics，Chinese Academy of Sciences， IGG)方案获得，即

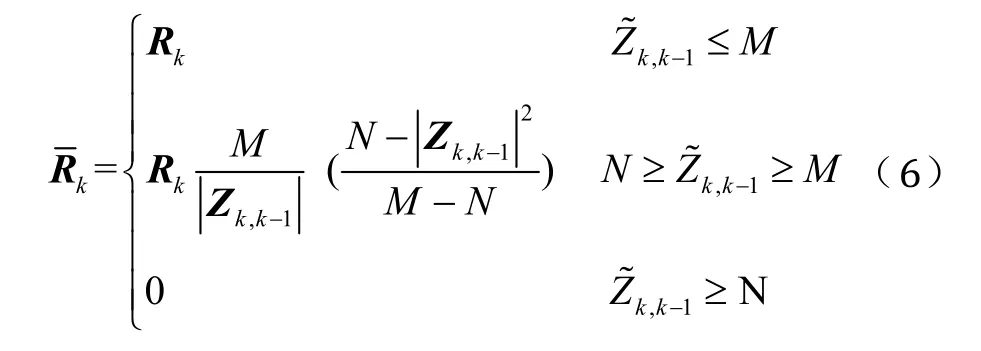
式中：M、N 为常值； ，1kkZ-˜ 为标准化残差。此方法可以直接利用观测值作为评判标准，计算量小，易于实现，但若系统未能检测到小周跳，仍会有较大误差出现。

1.2.2 卡方检验法

卡尔曼滤波是1 种线性最小方差估计，是1 个递推的过程，而在每1 步递推的过程中，残差是1 个很重要的信息来源，它包含有1 步预测误差信息。当导航系统发生故障时，残差序列会有异常变化。利用残差序列的这个特性，可以对故障观测值进行检测。此方法分2 步进行，即先对故障进行检测，再对有故障的观测值进行处理。卡方检验的方法在计算上较为复杂，但其检测精度较高，故本文 采用卡方检验的方法。

2 基于牛顿插值的抗差卡尔曼滤波算法

2.1 采用卡方检验的故障检测方法

2.1.1 卡方检验方法概述

由1 步预测值 Xk，k-1代替真实值 Xk引起的误差为： X˜k，k-1= Xk-X˜k，k-1。1 步预测与观测值相比较的差值为

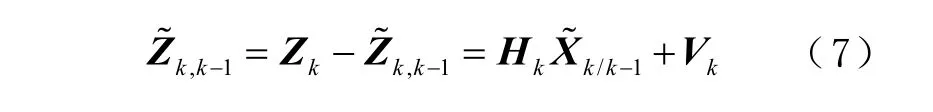
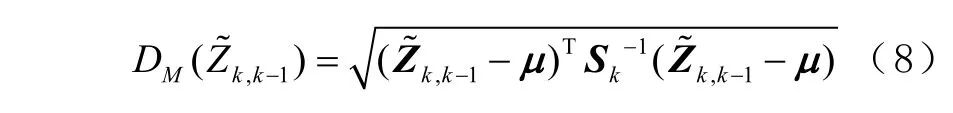
式中kS 为残差序列的协方差矩阵，即

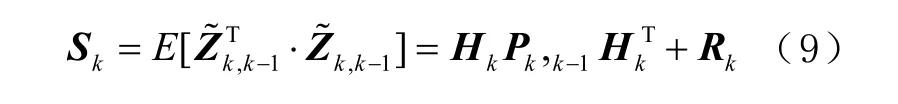
设 H0为原假设， H1为备选假设， H0、 H1分别定义为

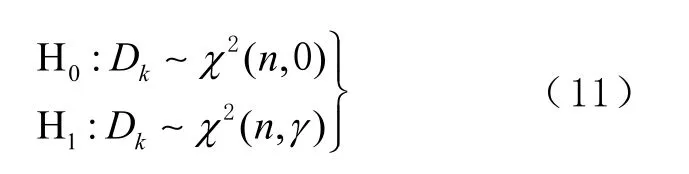
式中：n 为残差序列的维数；γ 为非中心化参数。取显著性水平为α，α 的大小直接决定了误差的判定条件的宽松程度。设检测量容许的最大值为T ( n )， T ( n) =( n)，一般将 T ( n )称为阈值，当检验量的值超过阈值 T ( n )时，认为发生故障[15-16]。

载体运动的过程中，引起观测值损坏的因素有很多，当出现链路中断等情况时，会造成当前时刻的观测值全部损坏；但有时可能只是因为个别仪器仪表的故障，并不会使观测值全部失效，这时若将当前时刻全部观测值当作故障值显然不妥，对导航精度也会造成一定影响。所以本文采用单个观测值的故障检测系统。设k 时刻第i 个观测值为 Dk( i )，这时的原假设和备选假设可以定义为

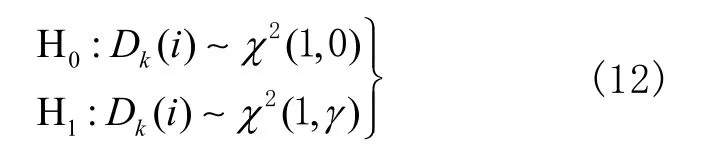
令 T (1)= χ2(1 ) ，当统计量 Dk( i ) ＜χ2(1 ) 时，认为系统无故障；当 Dk( i ) ＞ χ2(1 ) 时，认为导航系统观测值存在故障。

2.1.2 阈值的选取

在实际的运动过程中，载体所处的环境是比较复杂的，对观测值故障的容忍程度也会变大，所以选取的阈值也相对较大。当阈值选取过小时，会把一些正确的观测值当作故障观测值来处理，随着时间的推移会出现累积误差；当阈值选取过大时，被认定为出现故障的观测值就会变得很少，系统几乎检测不到故障，使抗差滤波之前和之后的曲线接近重合。

表1 为显著性水平α 和 ( )χ21 的分布表。

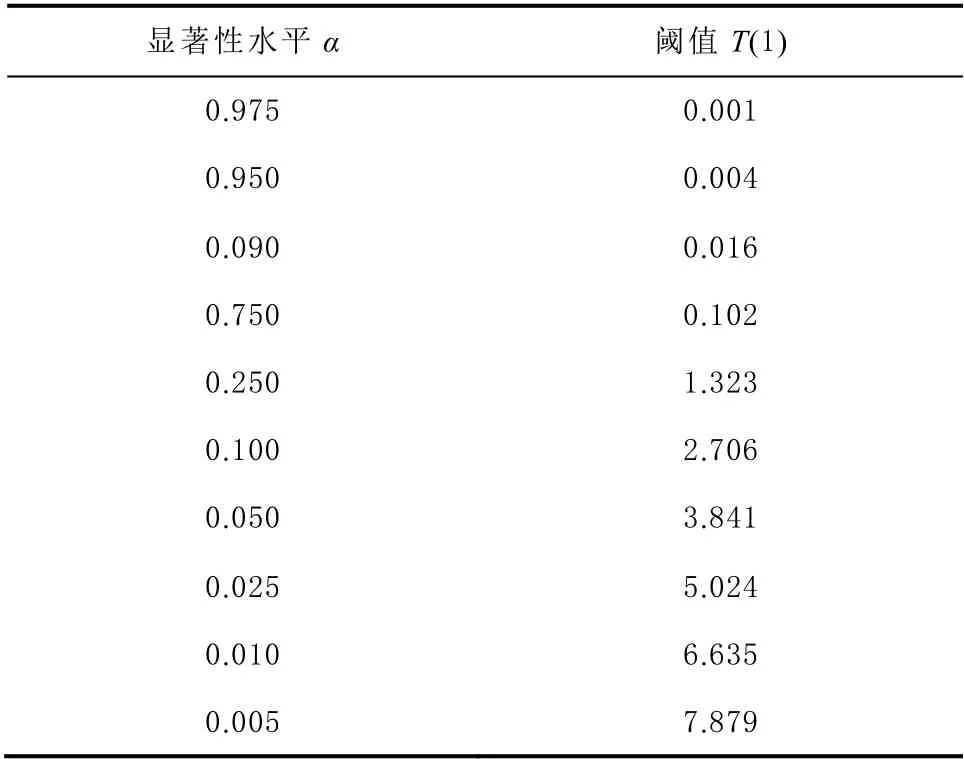
表1 显著性水平和阈值的关系

由表1 可知，显著性水平α 越小， χ2(1 ) 的值越大，故障的判定条件就越宽松。本文通过大量的实验分析，发现当显著性水平α 为0.25～0.01、阈值T (1)为5.024～6.635 时可以取得较好的效果，如图1所示。卡方检验统计量分布在6.635 以下的概率为 96.8%，以阈值为6.635 作为判定条件可以较为精确地检测到故障，误检的概率较小，所以本文选取6.635 作为阈值进行仿真验证。

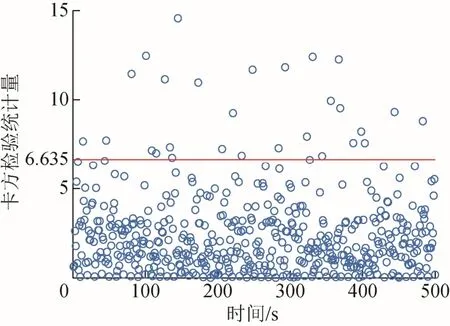
图1 卡方检验统计量分布

2.2 利用牛顿插值修正观测值

插值法[17]是利用已知函数 f ( x )某个区间的若干点，构造1 个近似函数 P ( x )来近似代替 f ( x )，牛顿插值可以根据计算精度灵活增加插值节点进行递推运算，公式形式对称、结构紧凑，容易编写程序。本文采用的牛顿插值方法是将近似函数P ( x )进行1 个单位的外延。

经典组合导航系统中，每次滤波过程的间隔时间一般是固定的，可以使用等距的插值公式，其表达式[18]为

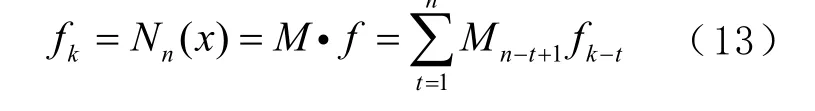
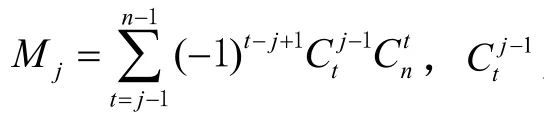
据式（13）便可用前n 个时刻的函数值对当前时刻函数值进行插值。

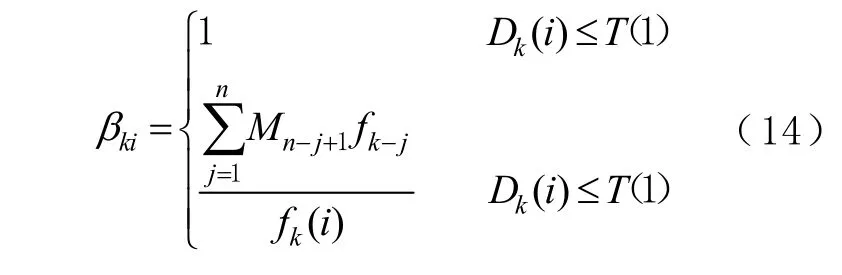
一般来说，插值节点取得越多，利用牛顿插值构造的曲线与原函数曲线近似程度越高，误差越小，适当增加节点数对计算结果的准确度是有帮助的，但并非插值多项式的次数越高越好。当插值节点增多时，不能保证非节点处的插值精度得到改善，有时反而误差更大。龙格现象表明，大范围内使用高次插值，逼近的效果往往是不理想的。根据大量实验验证，牛顿插值在4 阶时精度较高，出现龙格现象的概率也比较小，所以本文将以4 阶牛顿插值多项式来进行实验验证。基于卡方检验和牛顿插值的抗差滤波算法[13]为：

1）计算状态量的1 步预测值

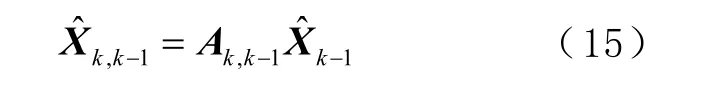
2）计算1 步预测的均方误差值

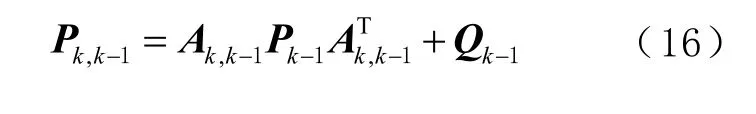
3）计算滤波增益值

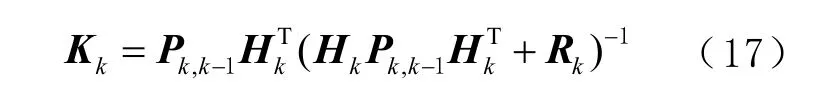
4）计算估计均方误差待下1 时刻使用

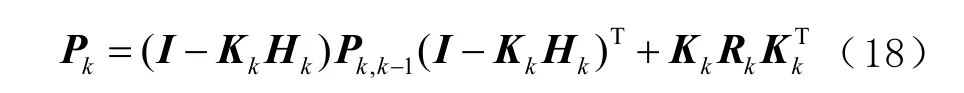
仿真步长为1 s，共用时500 s，为营造与飞机飞行相近的环境，人为地给观测值加入噪声，加入噪声的数值如表3 所示。

表3 随机噪声值

5）根据残差向量计算当前时刻 kD 值

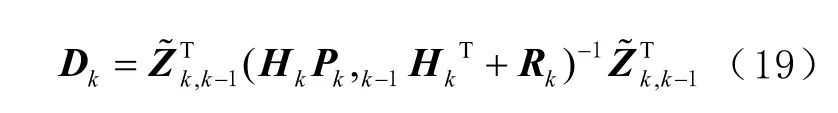
6）确定观测值

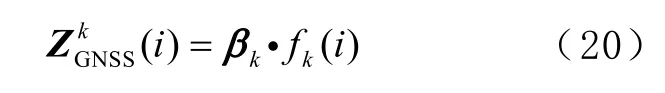
式 中 βk=Diag[β1， β2,… ,βn](i =1， 2， … , n)。

7）得到估计值

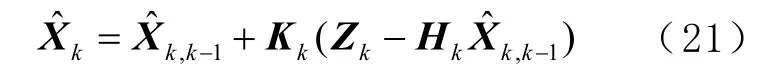
3 仿真分析及验证

3.1 仿真轨迹生成

本文模拟1 条飞机飞行轨迹来验证抗差滤波算法的有效性，飞行轨迹如图2 所示，将模拟的轨迹数据送入轨迹发生器，分别得到惯性导航系统(inertial navigation system， INS）和全球定位系统(global positioning system， GPS）的数据，各误差值如表2 所示。

为验证本抗差算法的有效性，制造量测不准确的外部环境，仿真在每隔10 s 的时刻加入1 个噪声放大系数m，使此时刻的噪声含有m 倍粗差。

3.2 分析与对比

本文对比使用上述抗差方法和不使用抗差方法的位置和速度误差，如图3、图4 所示。

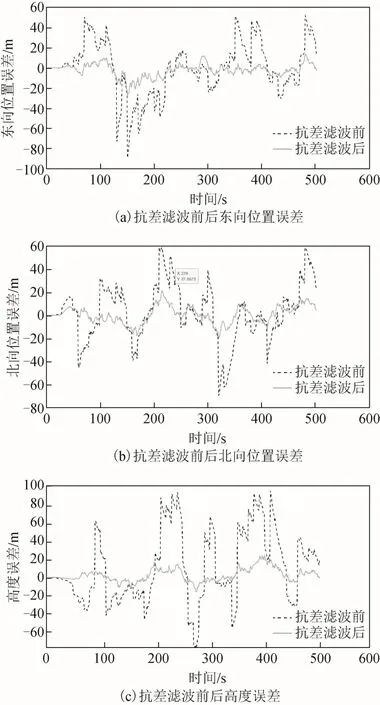
图3 抗差滤波前后位置误差

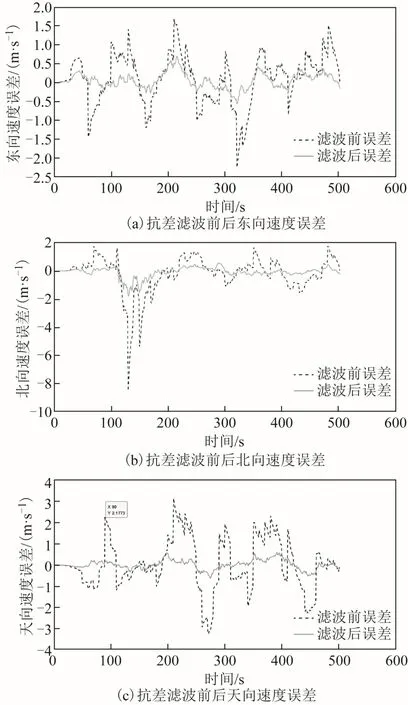
图4 抗差滤波前后速度误差

考虑到当GNSS 信号受到影响时，INS 仍然处于工作状态，分析对比了使用本文提出的抗差方法和仅使用INS 的误差，如图5、图6 所示。

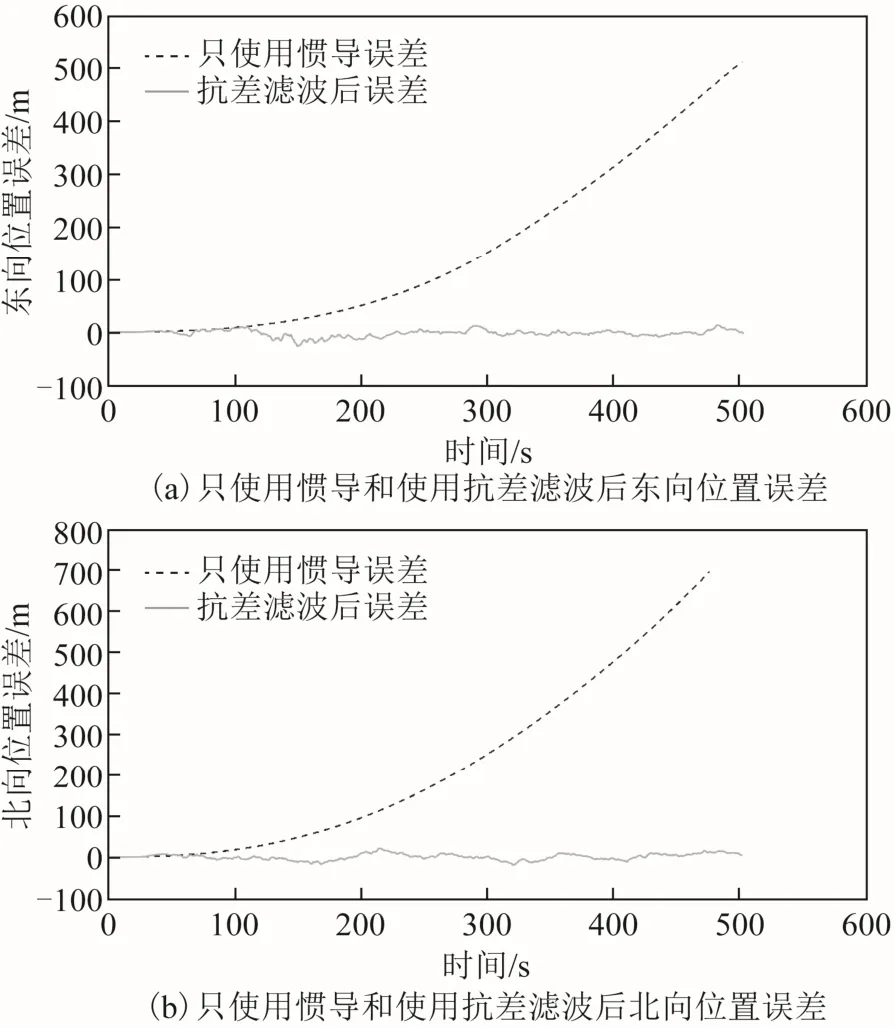
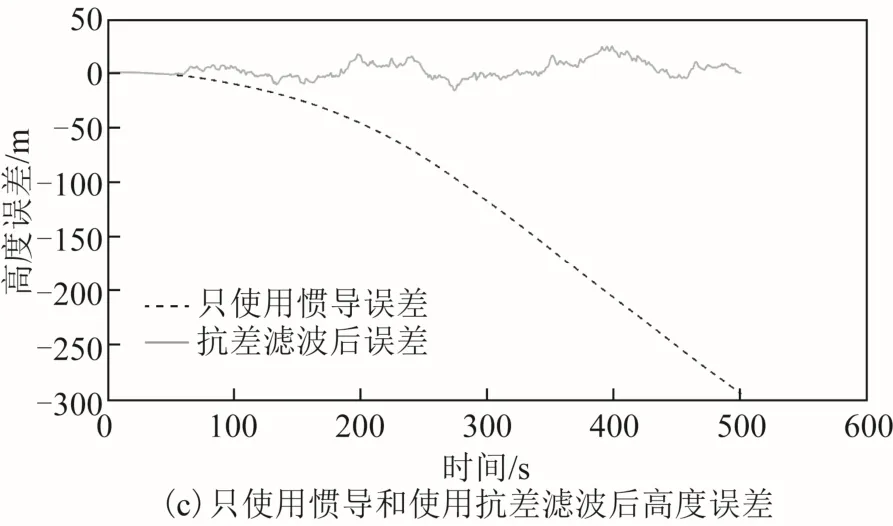
图5 只使用惯导和使用抗差滤波后位置误差

从图3、图4 可以看出，当不使用任何抗差方法时，由于GNSS 信号误差非常大，造成观测值发生急剧变化，如表4 所示。在使用本文提出的基于牛顿插值的抗差滤波方法后，对GNSS 所收到的观测值进行改良，使观测值恢复到正常范围，使位置和速度误差大大减小，如表5 所示。

惯性导航误差是随着时间逐渐增大的，没有卫星导航的实时修正，惯性导航方法无论是位置误差还是速度误差都会慢慢增大，与此相比，本文提出的基于牛顿插值的抗差滤波方法能较好地使误差维持在1 个较小的范围内，使导航精度得到提高，如图5、图6 所示。但不可否认的是，惯性导航在独立工作时间较短时，导航精度仍有一定的准确性。与此相比，由于在导航数据已有误差的前提下又人为加入噪声，致使使用本文提出的抗差方法在短时间内导航精度比只使用惯性导航精度略低，北向速度误差和天向速度误差在个别点处出现较大波动，如图6(b)、图6(c)所示。但北向速度误差值仍在-1.78～0.57 m/s，天向速度误差仍在-0.62～0.59 m/s 这样1 个较小的范围内，且随着时间的推移，惯性导航误差增大的现象慢慢显现出来。综合对比来看，基于牛顿插值的抗差卡尔曼滤波新算法仍不失为1 种有效的抗差滤波方法。

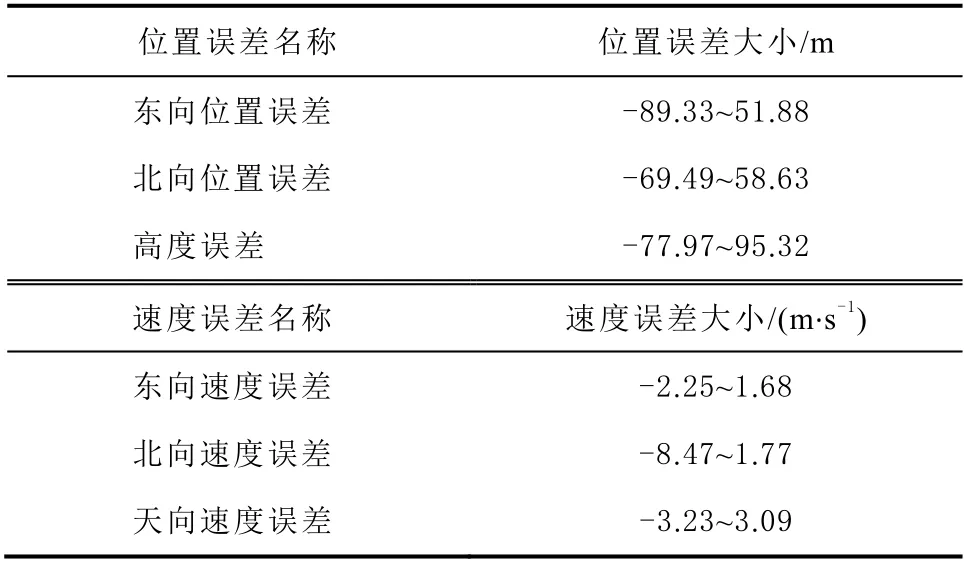
表4 抗差滤波前误差值

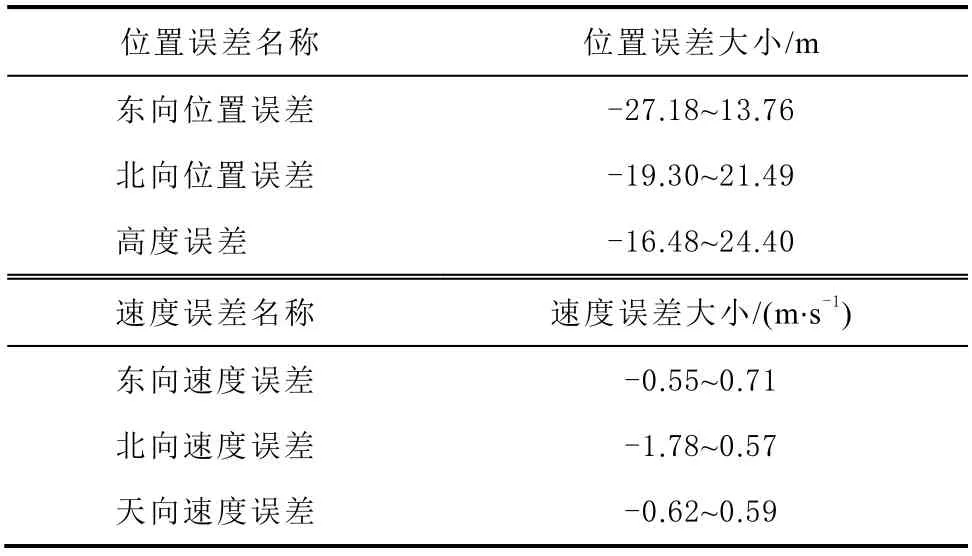
表5 抗差滤波后误差值

5 结束语

本文对 INS/GNSS 导航系统在运动过程中GNSS 信号会出现故障问题，提出1 种基于牛顿插值的抗差卡尔曼滤波算法。该算法通过当前时刻单个观测值的卡方检验方法，通过大量实验选取合适的阈值，对故障观测值进行更精确的定位。用过去几个时刻的观测值组成牛顿插值多项式进行外延，得到当前时刻观测值，给出了基于牛顿插值的抗差卡尔曼滤波方法的具体过程。最后，通过大量的仿真分析进行验证，该算法使误差控制在1 个较小的范围内，具有较好的抗差效果。该算法提高了抗差滤波系统的稳定性，计算简单，易于工程实现。