丰成分分析视角下的广东省经济发展研究

摘要：本文通过选择广东省21个城市的主要经济指标，采用sPss为主、EXCEL辅助的主成分分析方法，对21个城市的经济发展状况进行分析，并对结果加以说明，以期为广东省各城市发展提供借鉴，

关键词：主成分分析;广东省;经济发展

1基本思想

主成分分析方法是指用数学降维的方法，将很多个变量化为少数几个互相无关的综合变量的一种统计分析方法。主成分分析处理多维度变量的问题时，能够在有效信息足够多的前提下，提取少个变量加以分析解决，是一种便捷高效的运作方式。

2指标确定

根据科学性、系统性、可比性和操作性的原则，本文选取10个指标：

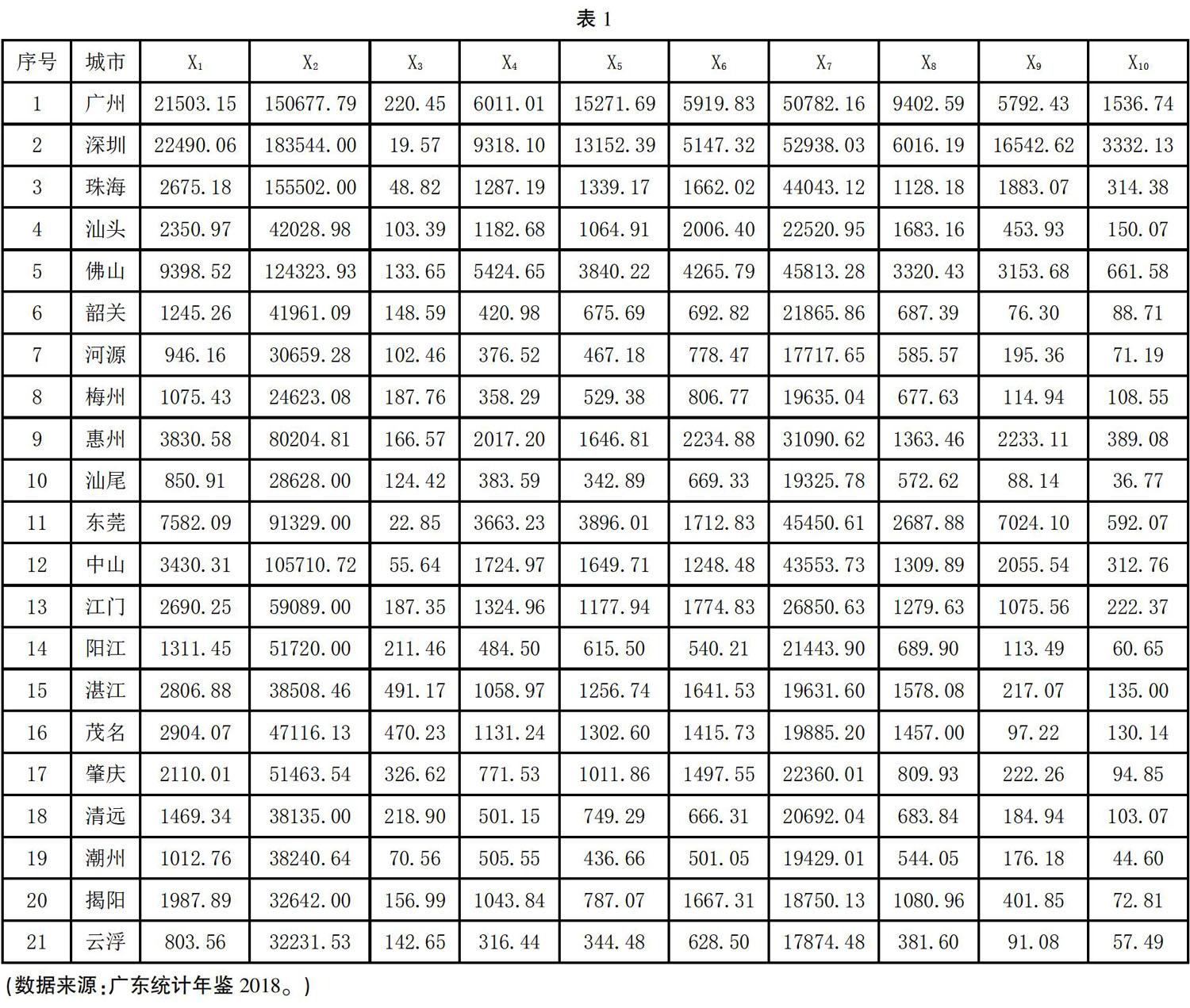
Xl-GDP（亿元）;X2-人均CDP（元）;X3-第一产业增加值（亿元）;X4-第二产业增加值（亿元）;X5-第三产业增加值（亿元）;X6-同定资产投资总额（亿元）;X7-常住居民人均可支配收入（元）;X8-社会消费品零售总额（亿元）;X9-出口总额（亿元）;X10-财政收入（亿元）。2017年各城市Xl-Xl0数据如表l所示。

3数据分析

将原始数据导人sPss，执行命令：分析一描述统计一描述，将原始数据标准化，所得结果如表2。

再进行主成分分析，结果如表3。

提取方法：主成份分析，如表4。

表4可以看出，共提取了两个主成分，两个成分的方差累计贡献率为90.476%（大于85%），且1、2分特征值都大于1，即该分析保留了原数据90.476%的信息，覆盖率极大，且为有效信息。

我们将两个主成分的特征值命名为l、2，由上表可知，1=7.889，2=1.159。

从成分矩阵可知，成分1中，X1、X2、X4、X5、X6、X7、X8、X9、Xl0具有較高的荷载，说明这九个指标相关性强;成分2中，X3 个个指标具有较高的荷载，该指标为第一产业增加值，即农业增加值，所以成分1、2可以理解为非农业和农业在经济发展中带动因素。 成分矩阵并不是主成分特征向量，也就是说不是主成分的系数，系数求法为：主成分载荷向量除以对应主成分特征值的算术平方根。我们利用excel计算主成分系数结果如下：

成份得分系数如表5。

根据成分得分系数矩阵，可以列出主成分解析的表达式，我们将主成分命名为Y.、Y2，则两者的表达式为：

Y，=0.349X1+0.318X2-0.106X3+0.347X4+0.3 39Xs+0.33 X6

+0.3 14X7+0.3 25 Xs+0.3 24Xg+0.333 X10

Y2=0.143 X1-0.177X2+0.846X3+0.01X4+0.187X s+0.221X6

-0.23X7+0.265 X8-0.15 8X9-0.018X10

如表6。

主成分的得分是对应因子得分与对应方差的算术平方根乘积。在本文中，具体数值如下：

主成分Yl得分=FACl_l*

主成分Y2得分=FAC2_1*

最后，根据主成分的贡献率对主成分得分进行加权平均，求得主成分综合得分：

Y=（Y1*78.889+Y2*11.587 /90.476

如表7。

4结束语

选择10个指标运用主成分分析方法显示，深圳排名第一，作为特区城市，出入境口岸多，对经济发展极其有利;紧接着就是一线城市广州，老牌大都市，经济发展一直都很迅猛。排名第三的佛山，是目前中国也是世界大型的制造业基地之一，外商投资企业的不断增加，有力地促进了国际贸易的发展。

对广东省21个地级城市进行分类，大致如下：第一等是珠三角城市，广州、深圳、佛山、东莞、珠海、中山;第二等是惠州、江门、汕头、湛江、茂名、肇庆;第三等为揭阳、阳江、韶关、清远、梅州、潮州、河源、汕尾和云浮。各个等级城市差异明显，第一等城市应继续发挥优势，保持稳定发展并持续拉动周边城市潜力，第三等城市应不断发挥创新，突破瓶颈，在粤港澳大湾区的国家战略层面上，主动出击，积极融人，利用契机，实现经济的飞速发展。

参考文献

[1]张文彤，邝春伟.SPSS统计分析基础教程（第二版）[M].高等教育出版社，2011.

[2]张瑜娟.基于主成分分析的广东省经济发展状况分析[J].经济视野，2015（ 03）.

[3]徐云鹏.基于主成分分析法的中部六省省会城市综合实力比较研究——兼论如何提升郑州城市竞争力[J].河南财政税务高等专科学校学报，2019（ 01）.

[4]陈伟清，赵文超，张学壵.基于主成分分析法的南宁市新型智慧城市建设研究[J].生态经济，2019（ 04）.

作者简介：华元果（19 84-），女，管理学硕士，广东中烟工业有限责任公司韶关卷烟厂经济师、统计师，研究方向为工业统计。