基于改进量子粒子群算法的火电厂再热汽温调节系统PID参数自整定

摘要：鉴于热控工作人员的技术水平和经验不足等问题，目前火电厂中许多控制回路整定效果不佳，因此PID参数的自整定具有极其重要的意义。为此，提出了一种基于改进量子粒子群算法的PID参数自整定方法，并采用MATLAB软件对火电厂再热汽温调节系统进行了仿真及PID参数自整定。通过与工程上的临界比例度法、传统粒子群算法、传统量子粒子群算法自整定的仿真结果相比较，证明了基于改进量子粒子群算法的PID参数自整定方法的优越性。

关键词：改进量子粒子群算法;PID;参数自整定;再热汽温调节系统;仿真

0 引言

人为手动整定PID参数，不仅耗时费力，而且整定效果与人员的整定水平息息相关，更无法获取令控制效果最佳的PID参数。因此，PID参数的自整定已成为国内外很多学者关注的焦点。目前已有不少PID参数整定的优化方法，比如蚁群算法、神经网络、遗传算法、粒子群算法等。粒子群算法（PSO）是典型的群体智能优化算法之一，具有参数较少、寻优能力强以及易于实现等优点[1]。但是该算法也具有一定局限性，因此国内外学者对传统粒子群算法进行了不同程度的优化[2-4]，Sun[5-6]等人结合物理量子理论，提出了量子粒子群算法（QPSO），但QPSO算法在后期迭代中存在陷入局部最优值的现象。

针对QPSO算法的缺点，本文通过引入扰动函数来更新粒子的物理位置，从而给予粒子摆脱局部最优的外部力量，克服粒子寻找质量停滞不前的问题，将粒子搜寻范围扩大，最终跳出局部最优范围，并将这种改进QPSO算法应用于火电厂再热汽温调节系统的PID参数自整定中，通过与工程上的临界比例度法、传统PSO算法、传统QPSO算法自整定的仿真结果对比，证明本文提出的改进QPSO算法具有更优越的性能，使再热汽温调节系统获得更好的调节质量。

1 引入扰动函数的改进QPSO算法

本文采用变异机制，引入扰动函数为QPSO算法提供一个外部力量，作为粒子摆脱局部最优的驱动力，改变粒子搜寻质量停滞不前的状态，将粒子的搜索空间扩大，帮助粒子跳出早熟的局面，采用的扰动函数如下：

式中，gbestk为第k代第i个粒子的个体历史最好位置适应度与群体历史最好位置;e为变异步距;N（0，1）为均值为0、方差为1的高斯随机分布，e越大，扰动越大，粒子跳出局部最优解的能力越强，但算法的收敛性能越弱，因此需要通过仿真选择适当的变异步距。

与此同时，为了既保证算法的收敛性能，又保证算法的寻优能力，上述变异机制仅用于算法的中期。

2 改进QPSO算法，优化再热汽温调节系统的PID参数

2.1    再热汽温对象动态特性

本文再热汽温控制系統PID参数优化和仿真所采用的模型如下[7]：

2.2    临界比例度法优化再热汽温调节系统PID参数

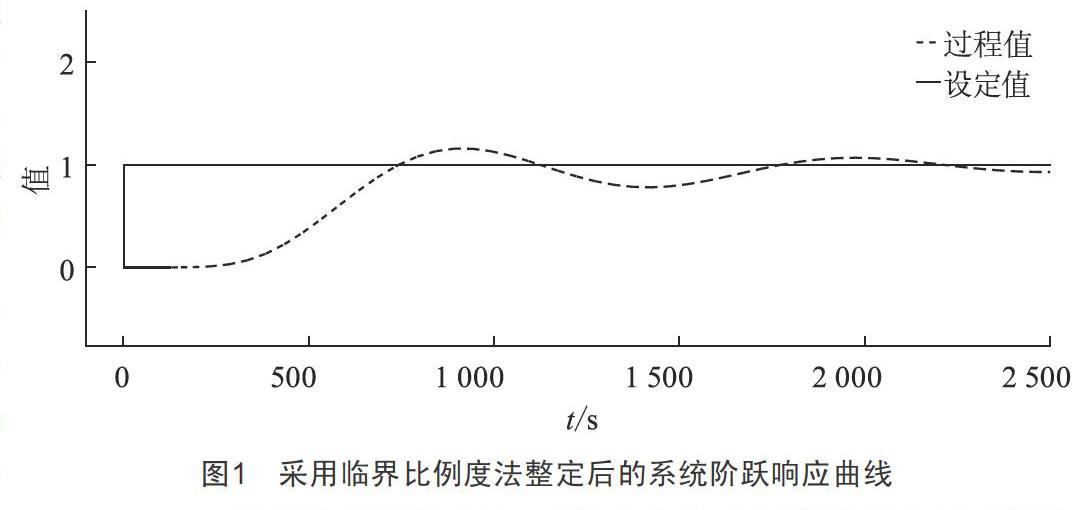
采用MATLAB软件对临界比例度法的PID整定进行仿真，得到该模型PID的各参数为：Kp=1.094，Ki=0.001 7，Kd=147.875，在此基础上，进行阶跃扰动试验，仿真结果如图1所示。

采用临界比例度法，系统产生临界振荡的条件是系统的阶数在3阶及3阶以上，否则易发生系统高频振荡，危及系统安全，因此在工程上实际应用临界比例度法整定PID参数具有一定的危险性和局限性。

2.3    传统PSO算法优化再热汽温调节系统PID参数

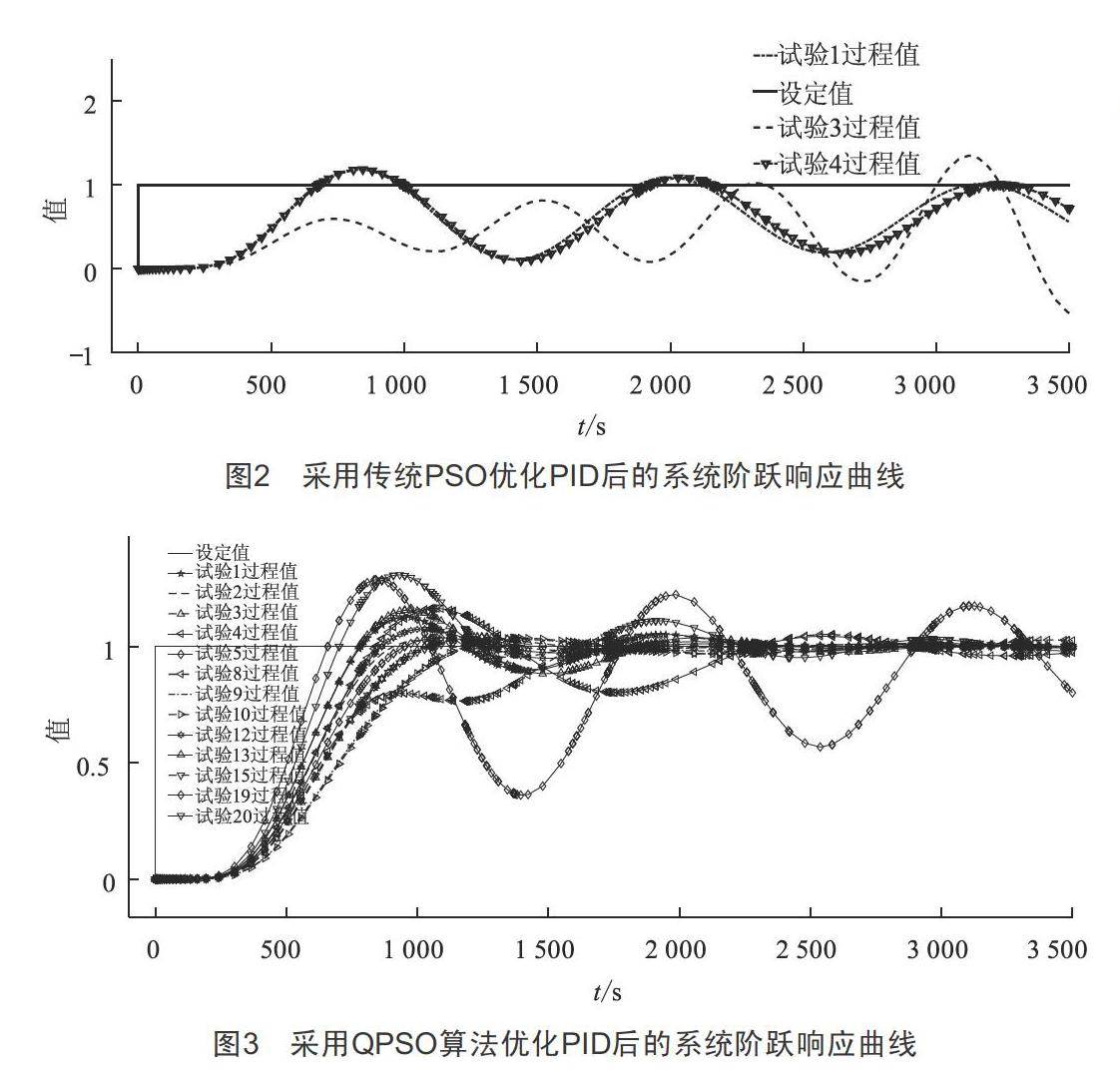
采用传统PSO算法优化再热汽温调节系统PID参数后，对系统进行仿真，结果如图2所示，可见采用传统PSO算法对再热汽温控制系统PID参数进行优化的效果差，甚至会得到令控制系统发散的PID参数，分析其原因为算法在早期迭代中就陷入了局部极值，无法寻求更优解。

2.4    QPSO算法优化再热汽温调节系统PID参数

鉴于上述采用传统PSO算法优化再热汽温调节系统PID参数的效果不佳，将优化算法改为QPSO算法，粒子群的种群范围为[10，500，500]，最优的PID参数约为Kp=0.713，Ki=0.001 6，Kd=104，其最优目标值为236 960。20次优化过程得到最优目标值小于2.4×105的次数为8，因此寻找到最优解的概率为40%。用所得的20组PID参数对系统进行仿真，结果如图3所示，可见采用QPSO算法对再热汽温控制系统PID参数进行优化的效果良好，不会寻优到导致系统发散的PID参数，具有不错的克服算法陷入局部最优解的能力，但通过试验发现算法收敛速度较慢，普遍需要种群进化150代后才能收敛。

2.5    改进QPSO算法优化再热汽温调节系统PID参数

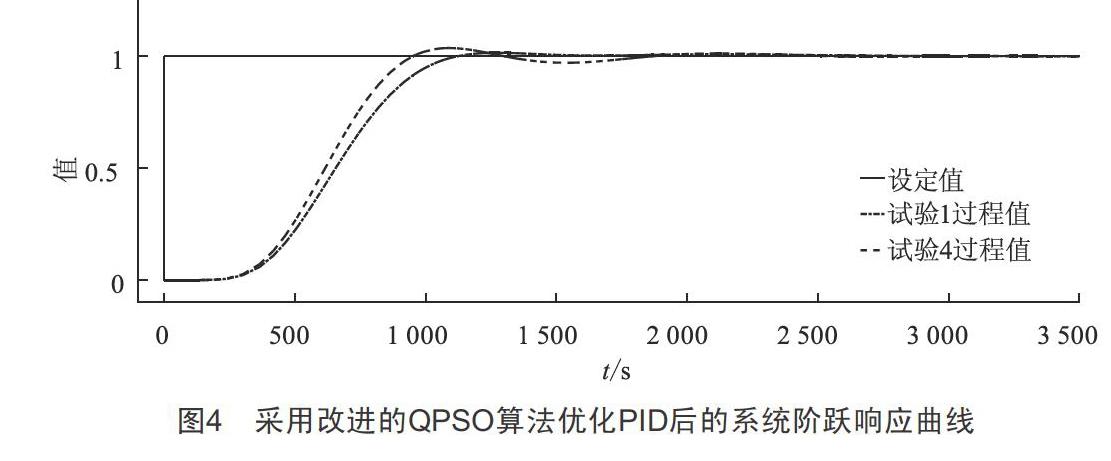
为进一步提升QPSO算法的寻优能力和收敛性能，本文对QPSO算法进行了改进，并采用该改进QPSO算法优化再热汽温调节系统PID参数，粒子群的种群范围为[10，500，500]，最优的PID参数约为Kp=0.713，Ki=0.001 6，Kd=104，其最优目标值为236 960。20次优化过程得到最优目标值小于2.4×105的次数为19，因此寻找到最优解的概率为95%。选取19组最优PID参数中的任意一组与剩余一组非最优PID参数，对系统进行仿真，结果如图4所示，即使试验1所得PID参数非最优，但其最优目标值为267 415，种群有效地向最优解收敛，因此采用该组PID参数的控制效果良好，可见采用改进QPSO算法对再热汽温控制系统PID参数进行优化的效果优异，且算法普遍在种群进化至60代时已经收敛，与QPSO算法相比，增加了种群在算法中期的粒子多样性，具有更强的克服算法陷入局部最优解的能力和收敛能力，在保证寻优效果的同时，大大缩短了寻优时间。

3 结语

本文通过分析采用传统粒子群算法和传统量子粒子群算法进行PID参数寻优过程中的优缺点，提出了一种引入扰动函数的改进QPSO算法，将改进的QPSO算法运用于再热汽温调节系统的PID参数优化，对优化后的控制系统进行阶跃扰动仿真试验，并与工程上的临界比例度法、传统粒子群算法、传统量子粒子群算法自整定的仿真结果对比，结果表明：将改进的QPSO算法运用于火电厂再热汽温调节系统的PID参数优化，具有更加突出的寻优能力和收敛性，使得系统具有优良的调节质量，既节省了人工整定PID参数的大量精力，又消除了因整定效果不佳而造成的系统振荡等危险因素。

[参考文献]

[1] 黄少荣.粒子群优化算法综述[J].计算机工程与设计，2009，30（8）：1977-1980.

[2] 朱蓉，靳雁霞，范卫华.融合优质粒子分布的粒子群优化算法[J].小型微型计算机系统，2015，36（3）：576-580.

[3] 许志良，曾徳炉，张运生.一种结合次梯度的粒子群全局优化算法[J].计算机应用研究，2015，32（4）：1007-1010.

[4] 印桂生，崔晓晖，董宇欣，等.面向离散优化问题的改进二元粒子群算法[J].哈尔滨工程大学学报，2015，36（2）：191-195.

[5] Sun J，Feng B，Xu W B.Particle swarm optimization with particles having quantum-behavior[C]//Proceedings of 2004 Congress on Evolutionary Computation，2004：325-331.

[6] Sun J，Feng B，Xu W B.A global search strategy of quantum-behaved particle swarm optimization[C]//

Proceedings of IEEE conference on Cybernetics and Intelligent Systems，2004：111-116.

[7] 楊红月，谷俊杰.再热汽温控制系统数学模型的建立与实验分析[J].电力科学与工程，2011，27（6）：51-56.

收稿日期：2020-03-03

作者简介：刘锦廉（1987—），男，福建龙岩人，硕士，工程师，研究方向：智能算法在模型识别及过程控制方面的应用。