经验小波变换及其在机械故障盲分离中的应用

吴加福，吴安定，肖 涵

（1．温州市特种设备检测研究院，浙江 温州 325000；2.武汉科技大学，湖北 武汉 430081）

1 引言

盲源分离是指在源信号和混合矩阵都未知的情况下，基于源信号之间相互独立的假设，从测得的观测信号中分离出源信号一种经典的信号处理方法。针对这个问题，Comon 提出经典的独立分量分析（Independent Component Analysis，ICA）方法，有效地解决了线性混合信号的盲源分离问题[1]。随后，在复数信号[2]的处理中提出了快速ICA 算法（FastICA），其给出局部一致的估计量，在频域盲分离中得到了广泛的应用。然而，传统的盲源分离仅适用于源数小于观测通道的情况下，而对于观测数小于源数的欠定情况效果不佳。针对欠定情况下的，学者提出了基于经验模式分解（Empirical Mode Decomposition，EMD）和主成分分析（Principal Component Analysis，PCA）的欠定去噪源分离方法[3]。文献[4]采用集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）、独立分量分析和连续小波变换相结合的方法，在克服ICA 中传感器数目大于源信号数目的限制条件时，获得了单通道含噪信号较好地分离。文献[5]提出了一种结合经验模式分解、奇异值分解（Singular ValueDecomposition，SVD）和贝叶斯信息准则（BayesianInformation Criterion，BIC）的源信号数量估计方法，解决了卷积混合的机械振动信号在欠定情况下的源数估计问题。但是，基于EMD 及其改进版本的欠定盲源分离方法都存在模式混叠、边界效应等问题[6-7]。拟运用经验小波变换[8]（Empirical Wavelet Transform，EWT）的理念进行单通道盲源分离，可以在一定程度上改善EMD 的缺陷。

单通道盲源分离是观测通道只有一个的特殊的欠定盲源分离，提出了一种基于经验小波变换（Empirical Wavelet Transform，EWT）的单通道盲源分离方法，使用EMD-SVD-BIC 方法估计源数以确定EWT 中频谱分割边界的个数N。再将傅里叶频谱转化为尺度空间表示，通过Otsu 算法[9]估计阈值T 并找到尺度空间中有用的模式，从而实现了经验小波在频谱上的自适应分割。同时，针对尺度空间在分割高频部分容易产生干扰模式的问题，通过保留尺度空间算法确定的前N 个边界频率，对N+1 个频带分别建立经验小波滤波器进行滤波，从而分解出N+1 个模式分量，其中N 个源信信号，1 个噪声信号，第N+1 个边界主要用于将噪声和主要独立分量分离。分别进行了仿真和实测数据的分析，结果显示该方法有很好的单通道盲源分离效果。

2 理论描述

2.1 盲源分离的模型

盲源分离的理论模型如下，m 个传感器测得的观测信号X=［x1（t），x2（t），…，xm（t）］T是n 个源信号S=［s1（t），s2（t），…，sn（t）］通过混合矩阵A∈Rm×n线性混合而成：

式中：V—噪声成分，单通道盲源分离是在观测通道只有一个（m=1）特殊情况的欠定盲源分离（m＜n）。

盲源分离的目的是基于源信号统计独立的假设，仅仅通过m 个观测通道寻求最优的分离矩阵（B∈Rn×m）用于独立分量的有效分离，从而获得源信号的最优估计：

2.2 基于EMD-SVD-BIC 的源数估计方法

拟采用EMD-SVD-BIC 进行单通道盲源分离的源数估计。主要包括3 个阶段的处理过程：

（1）对单通道观测信号进行EMD 分解，得到一组本征模态函数fIMF（t）=（c1（t），c2（t），L，cj（t），r（t））。然后将观测信号x 与本证模态函数组合成新的多维信号f1（t）=（x，c1（t），c2（t），L，cj（t），r（t）），并求其自相关矩阵Rf=E［f1（t），fH1（t）］。

（2）将Rf进行特征值（SVD）分解，并消除特征值为0 的元素，得到特征值向量。Rf的奇异值分解如下式：

式中：Λp—p 个按降序排列的主要特征值，Λp=diag｛λ1≥λ2≥λ3≥

L≥λp｝。Wp—p 个主要特征值对应的特征向量。Λp—T-p 个噪声特征值 Λq=diag｛λp+1≥λp+2≥λp+3≥L≥λT｝，T=j+2。Wq—T-p 个噪声特征值对应的特征向量。

（3）结合贝叶斯信息准则根据SVD 得的特征值估计源信号的数目。贝叶斯近似准则为：

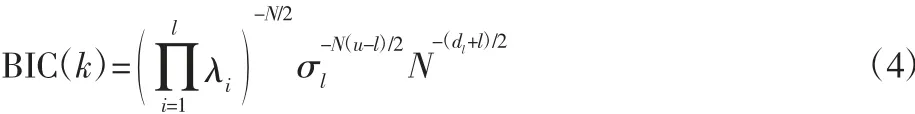
2.3 经验小波变换算法

经验小波变换是一种新的模式分解方法，其在小波变换的带通滤波之前，根据信号的频谱特性，设计一个合适的小波滤波器组进行频域分割，来提取信号的不同频段的局部特征。EWT 可以根据信号的自身特点选取合适的小波滤波器。

为了确定每个小波滤波器的频率范围，需要对信号的傅里叶频谱进行分割。对于频谱关于频率ω=0 对称的真实信号，建立一个以2π 为周期的归一化傅里叶轴，根据shannon 标准，限制ω∈［0，π］。设信号可分为N 个IMF，则归一化的傅里叶轴需在［0，π］范围内分成N 个连续片段 Λn=［ωn-1，ωn］，n=1，2，3，L，N，其中 ωn为各段的边界，且 ω0=0，ωn=π。N 个连续片段则需N+1 个边界，除去频谱自身边界0 和π，还需要确定N-1 个边界，而且关键是确定边界ωn的值。采用尺度空间算法分割频谱，从所有极小值能给定的分割开始，选择一个极小值并检测其相邻支撑是否属于同一模式。如果隶属于同一模式，则通过选定一个幅值最小的极小值删除其余的极小值来合并这些支撑。重复以上过程，直到不再出现可合并的极小值为止。根据文献[10]中的Littlewood-Paley 和Meyer 小波中的思想构建经验小波。如果任意n＞0，经验尺度函数和经验小波函数分别定义如下：

建立了经验小波基函数后，采用类似于传统的小波变换方法来定义经验小波变换。则细节系数Wεf（n，t）和近似系数Wεf（0，t）分别为：

接着对原信号进行重构，重构公式定义如下：

由以上公式得到调幅-调频单分量为：

2.4 基于经验小波变换的盲源分离方法

（1）首先用EMD-SVD-BIC 方法计算源数的估计值N，从而确定复合故障信号中有N 个源信号，加上多故障信号中的噪声信号则有N+1 个源信号。

（2）将复合故障信号的傅里叶频谱转化为尺度空间表示，通过Otsu 算法估计阈值T 并找到尺度空间中“有意义”的模式，实现经验小波的自适应分割频谱。

（3）复合故障信号中不仅包含源信号，还包含噪声信号，且噪声多数为高频分量。因而，拟保留尺度空间算法确定的前N 个边界频率，即保留整个频谱中低频区域获得的频谱分割边界。其中，前N-1 个频带是为把信号中多故障成分分离，第N 个边界主要用于将噪声和主要独立分量分离。

（4）对获得的N+1 个频带分别建立一个合适的经验小波滤波器，即以各频带中心频率为f 的带通滤波器分段进行滤波，从而分离出具有独立特性的分量，获得复合故障信号的N+1 个独立分量，其中N 个源信信号，1 个噪声信号。因此，可进一步提取不同故障的特征频率，实现多故障的分离及识别。

3 仿真分析

为了验证提出的方法在盲源分离方面应用的有效性，分析了滚动轴承的仿真信号。滚动轴承的振动信号一般包括调制分量、冲击分量和噪声分量。因此，构建一个仿真信号如下式：

式中：x1（t）—频率f1=60Hz 的冲击信号；x2（t）—调频信号，f2=300，fp=25Hz；n（t）—信噪比为5 的高斯白噪声。信号x（t）的采样频率设为fs=4000Hz，采样点数N=4000。此混合信号和各独立分量的时域波形，如图1 所示。

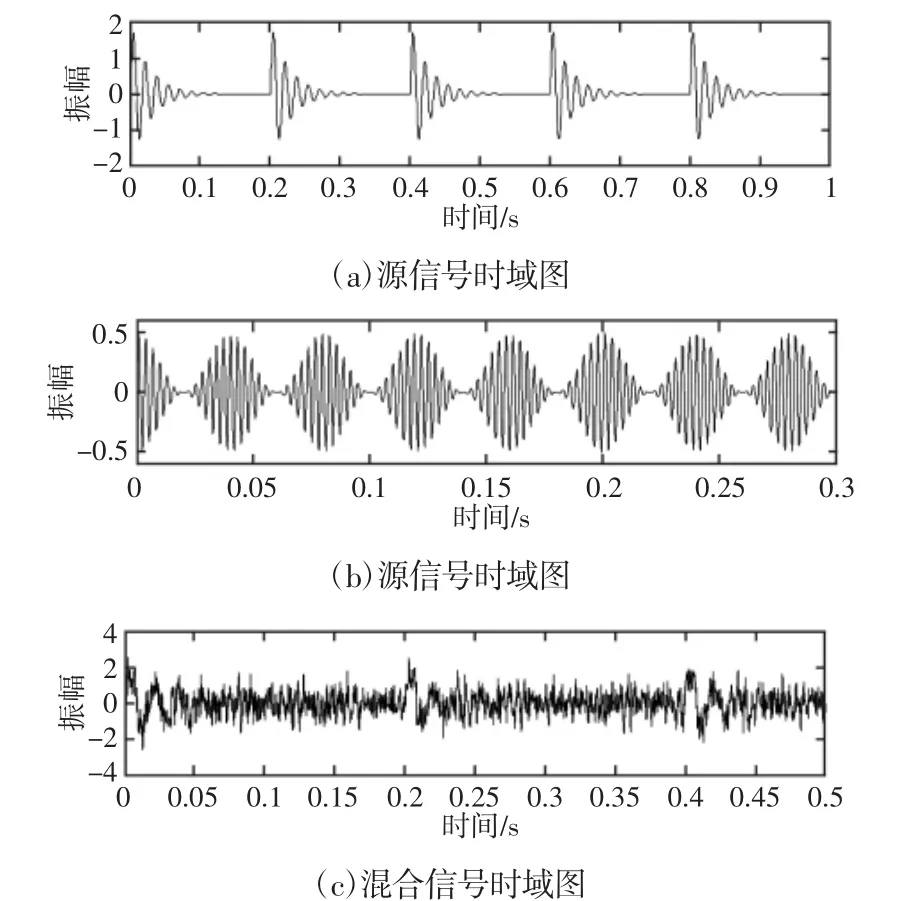
图1 混合信号和各源信号时域图Fig.1 The Mixed Signal and the Two Source Signals in Time Domain

从图1 可以观察到两种不同的源信号淹没在强背景噪声中，导致难以识别两种源信号的特征。采用提出的方法对混合信号进行处理，并选取EMD-fastICA 方法作为对比分析，验证其有效性。

首先采用EMD-SVD-BIC 方法估计源数，得到k 个BIC 值，如图2 所示。

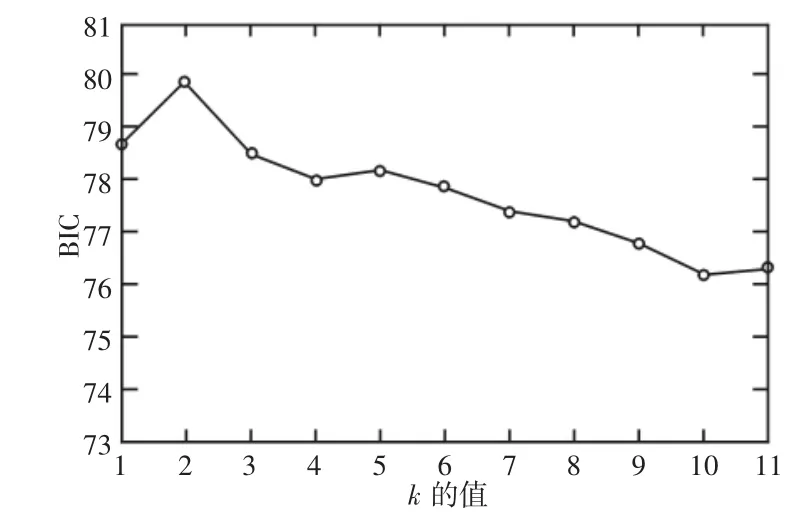
图2 仿真信号的BIC 的值Fig.2 The BIC of Simulation Signal

由图2 可知，N=2 时BIC 达到最大值，因此源信号数目为2。利用传统的EMD-fastICA 方法与提出的方法分别对该信号进行盲分离。

基于EMD-FastICA 的盲源分离方法，首先对仿真信号进行EMD 分解得到11 个IMF 分量，计算每个分量与仿真信号的相关系数。然后，以0.4 为阈值，取相关系数大于0.4 的分量相加构建第一个信号通道，以0.2 为阈值，取相关系数大于0.2 的分量相加构建第二个信号通道，则可以得到一个二维信号。最后，将该二维信号利用ICA 方法分离得到2 个分量，如图3（a）、图3（b）所示。即为恢复的两个源信号。可以观察到经过EMD-FastICA 分离得到的两个独立分量，与仿真信号中的源信号相比有些失真。因此，该方法不能较好地将混合信号中的源信号分离。

（d）恢复源信号x1（t），x2（t） 和噪声分量时域图

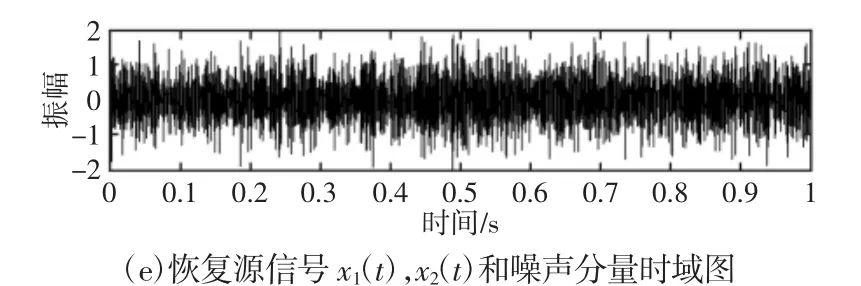
图3 EMD-fastICA 和这里方法的分离结果Fig.3 The Obtained Results by EMD-fastICA and the Proposed Method

将提出的基于EWT 的方法用来分析仿真信号，首先由于独立的源信号加上噪声成分一共有三个，因此EWT 中独立分量个数为3，即需频谱分割成3 段。再保留多故障信号频谱中较大的2个极大值，并取相邻平顶之间的极小值作为频谱边界频率。最后，用经验小波滤波器组对每段频带分别进行滤波，重构出完整的3个分量，即对应于盲分离中的2 个源信号，和1 个噪声信号。重构结果，如图3（c）、图3（d）和图3（e）所示。

从图中可以看到提出的方法可以有效地将两个源信号分离出来，得到的独立分量的时域波形图与源信号的时域波形基本一致。通过对比说明了提出的基于EWT 的盲源分离的性能比较优越。

4 实验分析

为了进一步验证提出的方法对于实测信号的有效性，采用了辛辛那提大学滚动轴承试验台的多故障单通道数据进行分析。实验装置，如图4 所示。实验中主轴转速为2000r/min，采样频率为20kHz，轴承是Rexnord ZA-2115 双列圆锥滚子轴承。实验中，轴承出现了内圈和滚动体复合故障。

图4 轴承故障实验台Fig.4 Rolling Bearing Test Table

选取采集到的轴承测量的复合故障信号作为分析对象，通过理论计算得到内圈故障频率fi=296.8Hz，滚动体故障频率fb=139.9Hz，转频fr=33.3Hz。该信号的时域图和频谱，如图5 所示。

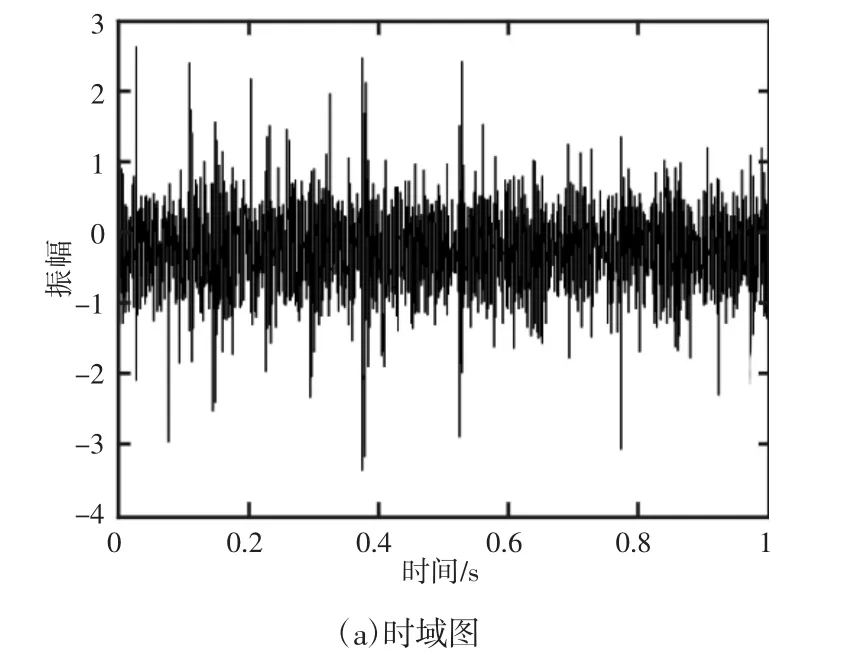
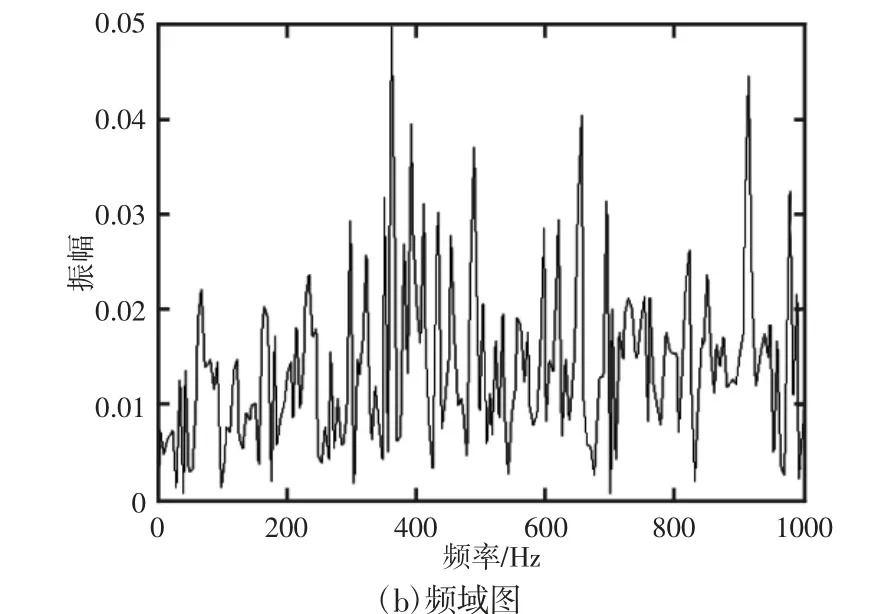
图5 实测单通道混合故障轴承信号Fig.5 The Measured Single Channel Mixed Bearing Fault Signal

可以看见原始信号的频域中找不到两个源信号的故障特征成分，因此源信号特征难以识别。分别采用提出的方法和EMD-fastICA 方法对实测信号进行分析。首先采用EMD-SVD-BIC 方法估计源数，可以得到源数为2。

EMD-fastICA 先将复合多故障信号用EMD 分解成14 个IMF 分量，并计算每个IMF 分量与原信号的相关系数。然后，以0.5 为阈值，取相关系数大于0.5 的分量相加构建第一个信号通道；以0.15 为阈值，取相关系数大于0.15 的分量构建第二个信号通道，构成一个二维信号。最后，利用ICA 方法分离该二维信号得到的2 个分量做频谱分析，如图6（a）、图6（b）所示。可以观察到恢复的两个信号的频谱图上无法看出轴承的故障信息和故障特征，因而EMD-fastICA 方法对于该实验信号的分析效果不佳。

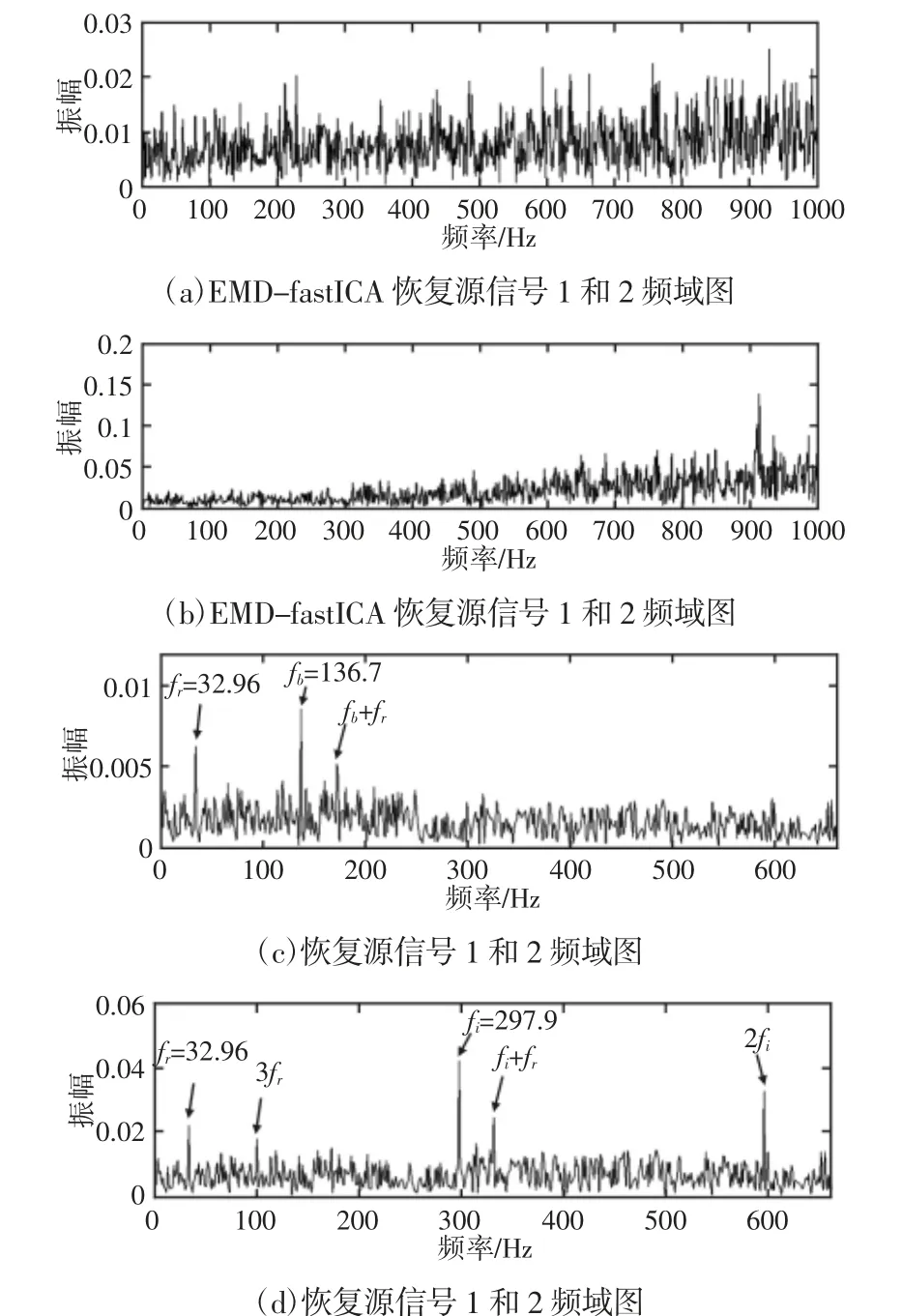
图6 EMD-fastICA 和本文方法的分离结果Fig.6 The Obtained Results by EMD-fastICA and the Proposed Method

用提出的方法分析实测信号，首先，设定EWT 中独立分量个数为3，即需频谱分割成3 段。用经验小波滤波器组对每段频带进行滤波，重构出完整的分量，即对应于盲分离中的源信号和噪声成分，分离得到的两个源信号频谱图，如图6（c）、图6（d）所示。由图可见，经过EWT 对复合故障进行盲分离获得的两个信号的频谱上可以容易的找到故障频率。在图6（c）中，转频32.96Hz 及滚动体故障频率136.7Hz 比较突出；而图6（d）中，转频32.96Hz、转频的三倍频99Hz、轴承内圈故障频率297.9Hz、故障频率的边频330.8Hz 以及故障频率的二倍频595.7Hz 可以轻易的找到。因此，可判断该齿轮发生了滚动体和内圈两种故障。因此，提出的基于EWT 的方法对于实测的轴承单通道混合故障有很好的分离效果，可以准确的提取故障特征成分。

5 结论

提出了一种基于经验小波变换的单通道盲源分离方法，并将其应用于机械设备轴承的故障诊断中。首先利用EMD-SVD-BIC对混合故障信号的源数进行准确估计，用于确定经验小波变换中频谱分割边界的个数。然后根据确定的边界个数来筛选尺度空间算法获得的边界。减少经验小波变换后容易产生无意义独立分量的问题。最后，将经验小波变换应用于单通道盲源分离领域，通过仿真实验和实测轴承混合故障数据的分析，并与基于EMD-fastICA 的盲源分离效果进行对比，证明了提出的方法对于轴承混合故障单通道信号有很好的分离效果，能准确的提取出故障特征成分。