全向移动机器人设计方案的综合评价研究

张 军，王古超，袁 翔，周宁宁

（安徽理工大学机械工程学院，安徽 淮南 232001）

1 引言

随着制造业和智能化技术的发展，移动机器人被用到了越来越多的地方，其中针对履带式、腿足式、普通轮式等运动形式的机器人的研究已经较为深入，然而对全向移动机器人设计的研究尚显不足，尤其是针对麦克纳姆轮全向移动机器人设计方案的综合评价研究仍处于起步阶段。得益于麦克纳姆轮自身结构的优势，使得麦克纳姆轮全向移动机器人具有良好的负重能力和运动性能，进而在仓储、港口等场合得到广泛应用，同时又由于麦克纳姆轮全向移动机器人整体结构相对复杂，部分设计指标模糊不定，所以难以通过单一的评估方法进行定量分析[1]，而且不同的设计人员往往具有不同的侧重点，则科学有效的指标评价模型和方法将是后续工作的关键，基于此以麦克纳姆轮全向移动平台为研究实例，提出运用一种熵权法改进的模糊层次分析方法对其设计方案进行综合评价，结果证明该评价模型与方法实用有效。

2 设计方案评价体系的构建

2.1 各层指标权重的确定

为了保证各指标的独立性，针对研究对象建立多层次分析模型，且每一层次中各元素下属的元素不超9 个，然后对各层元素就行两两比较，根据文献[2]提出的（1～9）标度法，对判断矩阵赋值，从而构建判断矩阵[3-4]A＝（aij）n×n。

根据所建立的判断矩阵求解指标权重，方法主要包括和积法、特征根法、方根法[5]，其中方根法的求解过程如下：

式中：wi—权向量W=［w1，w2，…，wi］的权重值；

λmax—判断矩阵的最大特征根。

为了保证评价结果的客观性，需要对判断矩阵进行一致性检验，即当CR＝CI/RI＜0.1 时，可以认为一致性检验通过，式中CI＝（λmax-n）/（n-1）为一致性指标，平均随机一致性指标RI 的取值[6]根据各判断矩阵的阶数n 查找，如表1 所示。

表1 平均随机一致性指标值Tab.1 Average Random Consistency Index

2.2 指标权重的修正

针对层次分析法所得指标权重存在主观性较大的问题[7]，现采用熵权法对其进行修正，具体过程如下：

式中：ej（0≤ej≤1）—第j 项指标的熵值；1/ln（n）—信息熵系数；uj—指标的信熵权重；lj—修正后的权向量L=［l1，l2，…，ln］的权重值。

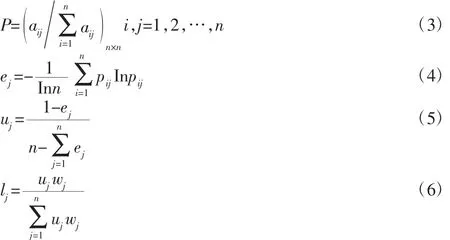
3 设计方案的综合评价

为了实现设计方案的综合评价，引入模糊数学的理论与思想[8]。设指标因素集U＝｛u1，u2，…，un｝，评语集V＝｛v1，v2，…，vm｝，指标因素ui（i＝1，2，…，n）属于评语集元素vj（j=1，2，…，m）的隶属度rij＝（ri1，ri2，ri3，ri4，rin），式中：0≤rij≤1。则模糊评判矩阵表示为：

令二级模糊评价向量Di＝Li＊Ri，则一级模糊综合评价向量D=L＊［D1，D2，…，Dn］T。综合评价结果多采用最大隶属度原则获得，由于忽略掉了其他隶属度的值，则会对评价结果产生影响，为了获得更加客观的评价结果，现根据评语集V 评分区间中间值建立评分集向量Q＝［Q1，Q2，…，Qm］，从而获得指标因素的综合评价值G＝D·QT，最后根据给出的等级划分标准得到综合评判等级，完成设计方案的综合评价。

4 麦克纳姆轮全向移动平台设计方案的综合评价

4.1 评价体系模型的建立

研究实例为一种麦克纳姆轮全向移动平台，实物如图1 所示。所示移动平台以四个麦克纳姆作为驱动轮，其中在轮子的轮缘上斜向分布着许多小棍子，当轮子绕固定的车轴转动时，这些辊子就会绕成一个圆柱面，进而可以实现连续的滚动，当各轮按照一定的组合方式一起运动时，则可实现平面内的三自由度运动[9-11]，即横纵向的平移运动以及自转运动。该平台采用“X 型”的轮系布局方式，运动原理，如图2 所示。其中平台上的箭头指向表示移动方向，轮子边的箭头表示该麦克纳姆轮的转动方向。在充分考虑该研究对象的特点后，归纳出其主要性能指标，建立设计方案的三级综合评价指标体系模型，如图3 所示。其中麦克纳姆轮全向移动平台综合性能作为目标层（A 层），环境生存属性、结构与功能属性、安全属性和绿色经济属性4 项一级指标作为准则层（B层），方案层（C 层）包括9 项二级指标。

图1 麦克纳姆轮全向移动平台实物图Fig.1 Mecanum Wheel Omnidirectional Moving Platform

图2 运动原理示意图Fig.2 Schematic Diagram of Motion Principle

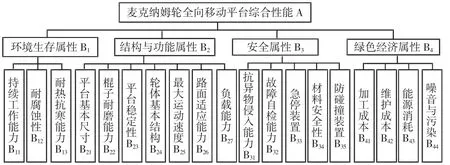
图3 麦克纳姆轮全向移动平台综合评价指标体系模型图Fig.3 Mecanum Wheel Omnidirectional Mobile Platform Comprehensive Evaluation System Model

4.2 指标权重的确定与修正

根据图3 的麦克纳姆轮全向移动平台设计方案的综合评价体系模型构建判断矩阵，包括准则层B 相对目标层A 的判断矩阵（记为A）、方案层C 相对准则层B 的判断矩阵（记为Bi，i=1，2，…，4），分别如下：

对已经构建的判断矩阵进行计算，得到各层指标权重大小，并完成一致性检验，为保证运算的快速性及计算精度，具体求解过程通过MATLAB 编程实现，最终结果，如表2 所示。运用熵权法对各级指标因素的权重进行修正，得到准则层

表2 指标权重及一致性检验结果Tab.2 Index Weight and Consistency Test Results

权重：L＝［0.0961，0.3351，0.2155，0.3533］。方案层权重：L1＝［0.6334，

0.0771 ，0.2895］；L2＝［0.0843，0.1560，0.2510，0.1194，0.0323，0.1434，0.2137］；L3＝［0.0581，0.0619，0.6604，0.0402，0.1794］；L4＝［0.1511，0.4853，0.0936，0.2700］。

4.3 设计方案的综合评价

本模型的评语共分五个等级[12]，即V＝｛v1，v2，v3，v4，v5｝＝｛优，良，中，较差，差｝，建立的评分标准与等级划分标准v，如表3 所示。

表3 评语集评分标度区间与等级划分Tab.3 Rating Scale and Grade Division

根据专家打分构造准则层模糊评判矩阵分别如下：

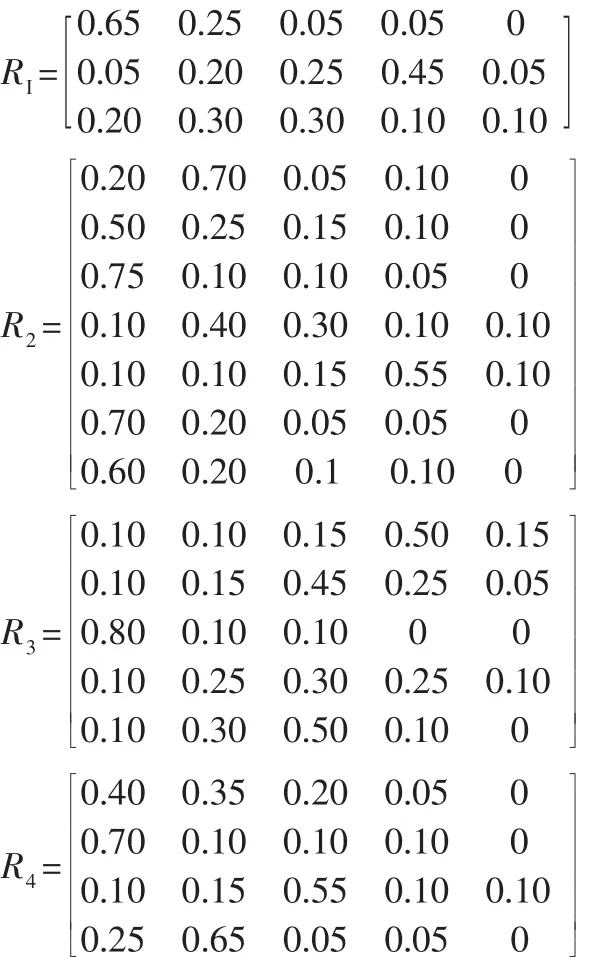
得二级模糊评价向量：D1＝L1＊R1＝［0.5714，0.2198，0.1205，0.0482，0.0402］；D2＝L2＊R2＝［0.5950，0.1865，0.1132，0.0675，0.0377］；D3＝L3＊R3＝［0.7319，0.0915，0.1243，0.0402，0.0121］；D4＝L4＊R4＝［0.5439，0.2810，0.0824，0.0777，0.0150］。

得到一级模糊评价向量：D＝L＊［D1，D2，D3，D4］T=［0.5679，0.2098，0.1081，0.0782，0.0360］，进一步得出麦克纳姆轮全向移动平台综合评价值为：G＝0.7391。从结果可知，该麦克纳姆轮全向移动平台综合评判等级为2 级，总体性能为良。

5 结论

全向移动机器人设计方案的综合评价是衡量机器人总体性能、提高设计指标科学性的重要基础，居于此提出了运用一种熵权法改进的模糊层次分析方法对其进行评价，通过对指标权重进行修正，不仅简化了针对全向移动机器人设计指标的分析过程，而且保证了评价结果的客观性和公正性。通过对麦克纳姆轮全向移动平台实例的测试分析可知，该平台未达到优等级主要是受到成本因素影响，而在稳定性、负载能力以及安全性等多方面均能达到预期效果，满足工作要求，从而验证了该评价模型和方法的有效性。