一种基于双目视觉的运动轨迹预测方法

杨勇强，唐 猛，孟 文，徐建龙

（西南交通大学机械工程学院，四川 成都 610031）

1 引言

准确地定位运动目标位置并预测轨迹，对信息处理以及决策制定有着重大的意义。近年来出现的定位技术有激光雷达定位、视觉定位、超声波定位、Wi-Fi 定位等。Wi-Fi 与超声波技术定位精度低且抗干扰能力较差，激光雷达有着较高的定位精度，但是成本高不易于推广。视觉技术可以更加快速、有效地定位运动物体，通过对图像信息的处理就可以完成一系列复杂的操作，大大提高了效率，降低了成本。视觉技术中常用到的是双目视觉。

有时为了实时跟踪目标还需要预测目标的运动轨迹。常用的轨迹预测方法主要有以下几种：卡尔曼滤波[1-2]，是一种从运动出发建立系统的状态和观测方程，从而递推估计的算法，由于无法获得准确的过程噪声，所以得到的预测位置不够精确。基于神经网络的预测[3]，是结合遗传算法以及反向传播算法进行轨迹预测，过程复杂且不具有较好的实时性。基于无监督学习的轨迹预测[4]在短时间内效果很好，但随着预测时间增长会出现较大的偏差。

为此，利用双目视觉系统精确定位运动物体的位置坐标，并采用多项式拟合的方法预测运动轨迹。双目视觉系统可以提供精确的历史位置坐标，多项式拟合可以根据目标前一时刻的几个位置较为精确地预测下一时刻的位置。

2 双目视觉原理

双目视觉是基于人眼视差原理的一项技术[5-7]。T是基线距离，f是摄相机焦距。设三维坐标系中的一个点P，它的位置坐标为（XP，YP，ZP）。假设左右两个摄像机的光轴是完全行对准的，且镜头无畸变。P点在左右两幅图像中成像点的横坐标分别为xl和xr。根据相似三角形关系即可推导出：

整理式（1）～式（3）可以得到摄像机坐标系中P 点的三维坐标。

3 摄像机标定

为了从二维图像中获得准确的信息，摄像机标定是双目立体视觉中的重要步骤[8-9]。如图1 所示，u 和v 为图像上定义的坐标系，代表图像数组中的列数与行数，该坐标系的原点为O0。建立一个用物理单位表示的图像坐标系，该坐标系的原点O1定义在图像平面与摄像机光轴的交点，若O1在以像素为单位的坐标系中的坐标为（u0，v0），两个坐标系的坐标有如下关系：

式中：dx—x 轴方向上每个像素的物理尺寸；dy—y 轴方向上每个像素的物理尺寸。

图1 图像坐标系Fig.1 Image Coordinate System

为了描述摄像机成像的几何关系，建立摄像机坐标系，其中原点O 为摄像机的光心，OO1为摄像机的焦距，ZC轴为摄像机光轴，XC轴和YC轴分别平行于图像坐标系中的x 轴和y 轴。

为了描述摄像机的位置，引入世界坐标系（XW，YW，ZW）。摄像机坐标系与世界坐标系之间的转换关系可表示为：

式中：t—三维平移向量；R—正交单位矩阵。

由中心透视投影关系可得：

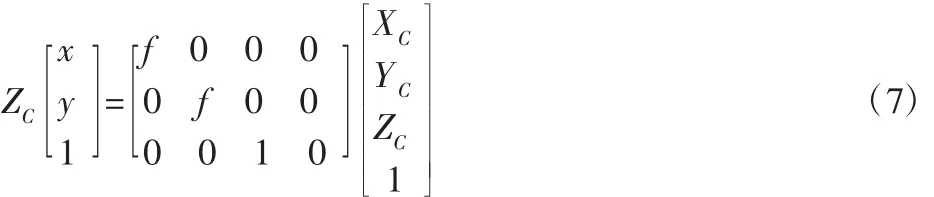
将式（4）～式（6）代入式（7）得投影点坐标与世界坐标的关系：

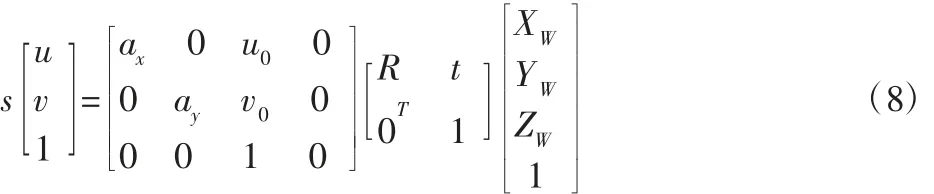
式中：s—比例因子；（ax，ay，u0，v0）—摄像机内部的参数；（R，t）—摄像机外部的参数。

本实验使用MATLAB2016b 中的Stereo Camera Calibrator 工具箱来标定双目摄像机。摄像机的标定需要借助标定靶标，将拍摄的10 组不同摆放位置的靶标图像导入Stereo Camera Calibrator App 进行标定。摄像机标定结果，如表1、表2 所示。

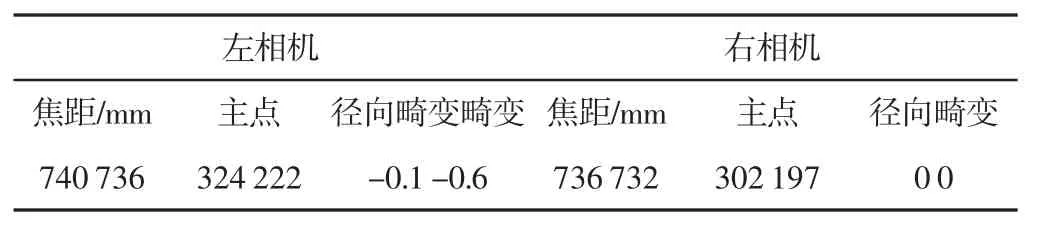
表1 系统内部参数标定结果Tab.1 Calibration for Internal Parameters of System

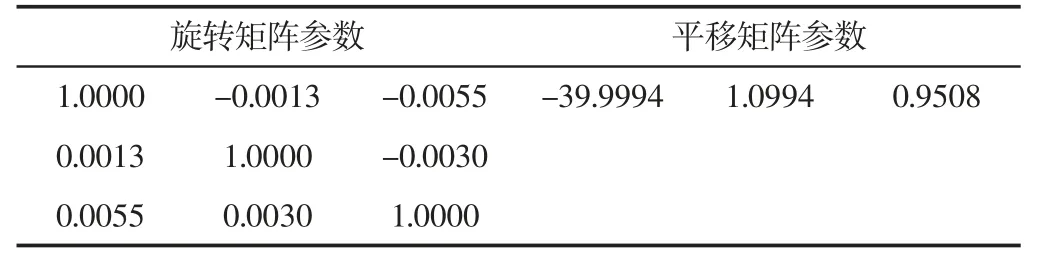
表2 系统外部参数标定结果Tab.2 Calibration for External Parameters of System

4 立体校正及图像预处理

在标定完成获得内外参数之后就需要对图像进行校正处理，通过建立左右相机的合成矩阵和行对准转换矩阵，使左右两摄像机图像平面平行[10-12]。

图2 运动物体识别流程图Fig.2 Flow Chart of Moving Object Recognition

要实现运动物体的轨迹预测，首先要将运动物体某时刻的空间位置坐标确定下来，这就需要从获得的图像中识别运动物体，处理步骤，如图2 所示。因为硬件设备的原因，当小球在运动过程中，摄像机捕捉到的图像具有“残影”，这时就不能简单地使用基于边缘检测的图像分割方法去识别图像中的小球，同时也无法求得图形的圆心（即三维空间中小球的球心）。通过观察，小球的颜色与背景的颜色差异很大，同时为了排除光照对图像识别的影响，将摄像机拍摄到的RGB 图像转化为HSV 图像，通过设置H 和S 的阈值进行图像分割，从而识别图像中的小球。

HSV（也称HSB）颜色模型是从调色板或者颜色轮中挑选颜色所采用的颜色系统[13]。HSV 表示的是色调（色相）、饱和度以及数值。这种颜色系统比RGB 更接近人们的经验和色彩的感知。

本实验中所用到的小球是橘黄色的，根据现有资料和反复测试规定H 的范围为：11～25，S 的范围为：250～255。

图3 运动物体识别结果Fig.3 Result of Moving Object Recognition

在图像中，HSV 颜色空间阈值分割之后，由于“残影”的原因，识别的形状不再是标准的圆形，而是不规则的图形，因此无法准确识别圆心。本实验中提出用不规则图形质心的位置近似替代圆形圆心的位置。

将带有“残影”的不规则图形视为一个匀质平面薄片，不规则图形所占面积为S，在不规则图形上任意处的密度为μ。在S 上任取一块小的封闭区域dσ，这一块小区域的面积可求，由此可得静矩元素：

将静矩元素S 上积分后可得到静矩，静矩比上质量为质心坐标，即可求得质心坐标。

5 特征匹配

立体匹配的本质是在左右图像中找到相应的点，然后获得视差。考虑到匹配速度和准确度这里应用semi-global matching算法求解视差，它的思路是选取图像中每个像素点的视差，组成一幅视差图，设置一个和视差有关的全局能量函数，使这个能量函数值最小，以达到求解每个像素最优视差的目的。匹配完成之后可以得到的视差图，如图4 所示。通过视差图还原三维信息。

图4 视差图Fig.4 Parallax Diagram

6 三维重建

经过匹配之后，得到视差图以及一系列空间上离散的点，对这些点赋予深度信息并逐一剖分，从而得到三维重构模型。

三维重建是基于两幅或者多幅图像恢复三维信息的方法。摄像机通过透视变换获取了三维空间物体的二维图像，在图像上的点与实际物体上的点存在着一定的对应关系。通过之前完成的相机标定、图像预处理、图像匹配等步骤，由视差图和标定结果得到空间三维坐标。

因为单摆运动可以看成是一个二维平面运动，其Z 方向上的坐标几乎不变，由计算结果可以绘制出的物体运动的位置散点图，如图5 所示。

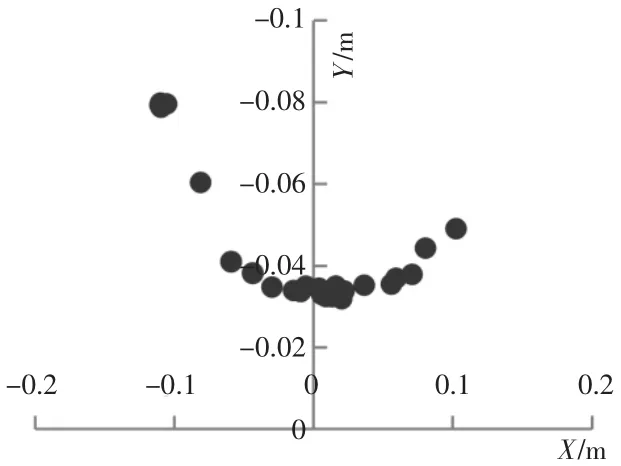
图5 散点图Fig.5 Scatter Plot

7 轨迹预测

运动轨迹是关于时间的函数，运动物体每一时刻的位置都会随着时间的变化而变化，但总是在一条确定的曲线上。由此可以建立一个多项式函数去拟合曲线从而达到逼近运动轨迹的目的，由最小二乘法求解出运动物体位置坐标的预测值。

根据多项式拟合运动轨迹的目标位置预测算法，认为运动物体位置坐标的预测值与最近几个坐标值有关。针对双目摄像机获得的图像，选用二次多项式作为拟合函数表示单摆运动轨迹。

设二次多项式为：

若拟合m 个数据点（xi，yi）（i=1，2，…，m），用Ri来表示f（x）在xi点的值与yi的偏差，将m 个数据点代入得到：

式（11）的解改写成矩阵的形式，即可求解pj（j=0，1，2），最后外推一点得到下一时刻目标位置的预测值ym+1：

本实验经多次计算，设定m 等于4，将已知坐标值代入公式得到如下表所示的预测值。

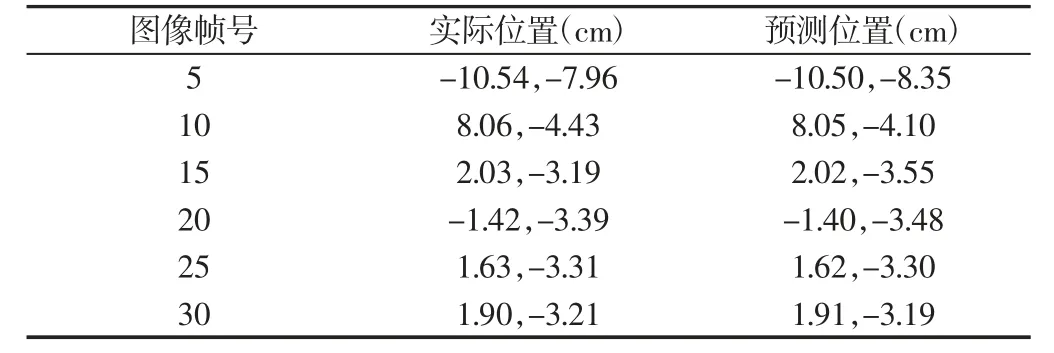
表3 目标位置的实际值和预测值Tab.3 Actual and Predicted Values of the Target Location

8 结论

提出了一种以双目视觉为基础的运动位置检测以及位置预测的方法。它能够对目标物体的位置进行快速检测，并根据当前的目标位置较准确的预测出下一时刻运动物体的位置。实验已经证明了这种检测以及预测方法具有较快的速度和准确性。

针对运动物体的轨迹预测也可以采用SVM 以及循环神经网络等方法，这些方法能够达到更好的预测效果，并且能够用于更复杂的环境，这是下一步的研究重点。