管道检测机器人机构ADAMS 动力学仿真分析

李颖欣，刘满禄，李新茂

（西南科技大学，四川 绵阳 621000）

1 引言

随着石油、化工、天然气及核工业等产业迅速发展，管道作为一种的物料输送设施显得尤为重要。在上述特殊环境中作业的管道，特别是在核工业环境下的管道，由于长期处于恶劣的环境下，会不可避免地出现裂纹、变形等现象，并且人们很难直接维修管道。考虑到传统的管道检测方法存在工程量大、准确率低等缺点，因此目前管道的维护和检测通常采用管道检测机器人来进行[1-3]。

现有管道机器人根据驱动方式的不同分为流动式机器人、履带式机器人、腹壁式机器人等类型，而轮式机器人驱动因其效率高、运行平稳的特点成为管道机器人的主要驱动方式[2]，然而遇到弯管或不规则管道，如发生变形、管内壁不平整的管道，就会发生运动干涉等问题。因此针对以上问题[3]，研究了一种具有自适应性、运动灵活、实时可靠的管道检测机器人，通过Creo 建立三维模型，导入ADAMS 中并完成其运动控制的仿真，为后续的样机的建立理论基础。

2 管道检测机器人模型

由于管道检测机器人的工作环境非常复杂，通常工作在封闭的空间，其中包括水平直管、各角度弯管、斜坡管、斜坡管以及变径管接口等，它的运动距离一般也较长。针对我国管道的复杂性特点，设计出一种管道检测机器人，可通过内径在（180～240）mm 范围内变化的圆形管道，其类型包含直管、弯管、三通管。同时为了避免当管道变形量过大，管道机器人回退时易发生卡死现象，而限制轮式机器人的作业环境，提出具有双向越障能力的驱动单元，可满足轮式机器人在弯管或不规则管道内的双向越障要求。为保证管道检测机器人具有良好的自适应性且能承载相应的检测器件等。管道检测机器人机构分为驱动单元和控制单元，总体分为三部分，前后两部分为驱动单元，中间部分为控制单元。

图1 管道检测机器人实物图Fig.1 Physical Picture of Pipeline Detection Robot

3 管道检测机器人机构研究设计

3.1 通过性研究

管道检测机器人只有本体机构满足弯管及三通管的几何约束和运动约束时[4]，才能顺利完成作业任务，以防出现卡死或者较大的动力损耗现象。机器人的弯管通过性需要考虑以下两种情况：（1）机器人两端在直管部分；（2）机器人两端在弯管部分。

①机器人两端在直管部分，需满足以下不等式：

式中：w—机器人本体宽度；hm—机器人本体最大长度；2Ф—管道弯曲角度；R—管道曲率半径；D—管道直径。

当满足以上要求时，机器人即可通过弯管。同弯管比较，管道机器人通过三通管的条件更加苛刻，三通管的通过难点在于机器人的转向问题，解决办法为通过控制驱动电机旋转方向，达到选择性转向的目的。经过计算确定，管道检测机器人驱动单元长度h 为200mm，宽度范围在（160～240）mm 之间。

3.2 管道机器人机构的变径越障原理设计

双向越障驱动单元的机构原理图，如图2 所示。该驱动单元为四分支结构，采用多电机驱动。由驱动部件、变径越障部件组成。每个驱动部件都装有一只电机，通过齿轮副、锥齿轮传动，驱动车轮旋转。采用四分支结构，避免当管道机器人的非车轮部分接触地面。变径越障部件采用多连杆副与预紧螺旋副配合的结构，由连杆、预紧弹簧、预紧螺旋副组成，采用双四边形机构，令机器人前进后退都能具备一定的越障能力及自适应管径变化的需求[5]。

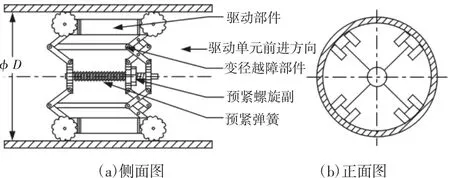
图2 双向越障驱动单元的机构原理图Fig.2 Mechanism Schematic Diagram of Two-Way Obstacle Drive Unit

管道机器人的双向越障驱动单元按功能需求可分为越障功能部分及变径功能部分，实则采用同一机构来实现两功能。

3.2.1 管道机器人机构的越障功能部分

为了提高机器人的越障能力，设计了如图3 的双向越障机构。采用双平行四边形机构，令机器人驱动单元能够越过两个方向的障碍。通过与图4 现有的平行四边形机构的受力做比较，平行四边形机构只有良好的单向越障能力，而当机器人进行后退操作时，容易发生运动干涉；而图3 所设计的双四边形机构，可以良好地处理两个方向的越障问题，令机器人能够在环境恶劣的管道中完成各种作业需求。

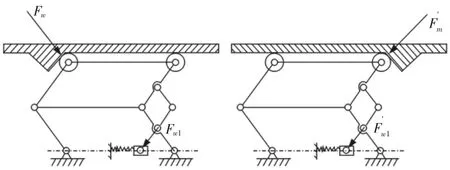
图3 双四边形机构的受力简图Fig.3 The Force Diagram of the Double Qua Drilateral Mechanism

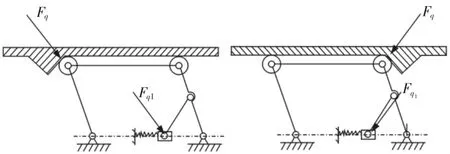
图4 平行四边形机构的受力简图Fig.4 aSchematic Diagram of the Force of a Parallelogram Mechanism

3.2.2 管道机器人机构的变径功能部分

双向越障机构的变径功能部分，与越障功能部分使用同一机构，即双平行四边形机构，利用平行四边形的对边平行及四边形不稳定的几何原理，实现自调节机器人中心距管内壁距离的目的，机器人的自调节性由套在预紧螺旋副上的预紧弹簧提供。

3.3 管道检测机器人越障参数分析

提出的管道检测机器人的双向越障驱动单元采用具有自适应性的双平行四边形机构，该结构更适用于通过连续变径的管道，而不擅长通过突然出现的障碍。对于此种障碍，管道检测机器人受力分析图，如图5 所示。

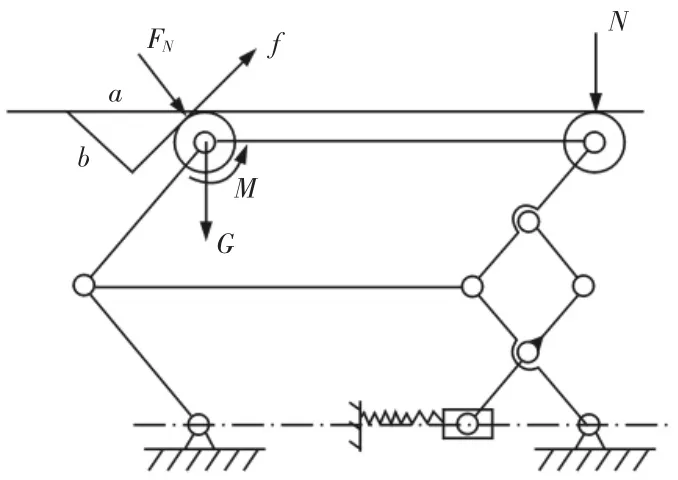
图5 管道检测机器人受力分析图Fig.5 Force Analysis Diagram of Pipeline Detection Robot

要使管道检测机器人成功越过障碍，需要满足以下平衡条件：

当机器人越过最大高度的障碍物时，可得到公式：

式中：M—驱动轮存在的转矩；

G—驱动轮自身会受到的张紧力；

FN—障碍物对驱动轮存在正压力；

f—驱动轮与障碍物的表面之间存在切向摩擦力；

N—驱动轮与管壁存在预紧力；

R—驱动轮半径。

通过以上计算可知，管道检测机器人越障的最大高度应小于hmax。

4 ADAMS 模型建立

由于管道检测机器人由四分支结构组成，且呈十字分布，均采用相同的电机驱动，故对管道检测机器人变径和越障动作控制可分析转化对一个驱动单元的控制分析。在Creo 中建立管道检测机器人的三维实体模型，存为ParaSolid 格式[6]；然后启动ADAMS软件新建一个模型；进入工作窗口，在File 功能中选择Import 将建立好的模型导入ADAMS 中，如图6 所示。

图6 ADAMS 中的三维模型Fig.6 Three-Dimensional Model of ADAMS

根据机构中各个部件之间的运动关系和受力作用，建立运动副、接触和压簧的情况，将机构放在直径范围为（240～180）mm的管道中以及机器人两边存在障碍物的模型中，仿真情况，如图7、图8 所示。为了实现管道检测机器人在管道中行进动作，需要在四个轮子上的旋转副上施加四个旋转驱动Motion_1、Motion_2、Motion_3 和Motion_4，对其设置不同的运动参数即能得到不同运动速度下的管道检测机器人的运动情况。

图7 变径运动仿真模型Fig.7 Variable Diameter Motion Simulation Model

图8 双向避障运动仿真模型Fig.8 Simulation Model of Bidirectional Obstacle a Voidance

4.1 ADAMS 仿真基本参数设计

ADAMS 仿真时，需要对基本参数进行设计并设置，才能得到与实际情况相符的仿真情况。

4.1.1 弹簧的阻尼系数与刚度系数

对管道检测机器人进行运动仿真时，需要根据实际情况确定压簧的刚度和阻尼系数，弹簧刚度是弹簧产生单位变形时所需的载荷，即：

式中：k—弹簧的刚度；

F—弹簧所受的载荷；

λ—弹簧在受载荷F 时所产生的变形量；

G—弹簧材料的切变模量；

d—弹簧丝的直径；

n—弹簧的有效圈数；

C—弹簧的旋绕比。

因为普通弹簧的阻尼很小可忽略不计，考虑在实际运动中，弹簧仍然存在阻尼损耗，因此在这里弹簧阻尼设置为0.01，弹簧刚度设置为0.4。

4.1.2 材料定义与参数设置

在ADAMS 中，需要对各构件的材料进行定义以及弹性模量、泊松比和密度参数的设置，才能完成后续的运动学仿真，模型中部件命名与材料列表[7]，如表1 所示。

表1 模型材料列表Tab.1 Model Material List

4.1.3 静摩擦系数与动摩擦系数

管道检测机器人在运动时必定会与管道表面接触，经过查表得，材料钢和材料橡胶的静摩擦系数约为0.9，动摩擦系数约为0.6，即在ADAMS 中，需要在建模工具条Forces 中单击接触按钮，在弹出的创建接触对话框中，将动摩擦系数和静摩擦系数设为0.6 和0.9[8]。

4.2 双向越障驱动单元仿真结果分析

4.2.1 正向越障仿真结果分析

机器人正向越障图，如图8（a）所示。轮子半径为20mm，假设障碍物为42mm 高，设置仿真时间为15s，步数为50。随着时间的增加，压簧受力情况[9]，如图9 所示。管道检测机器人压缩位移变化曲线，如图10 所示。

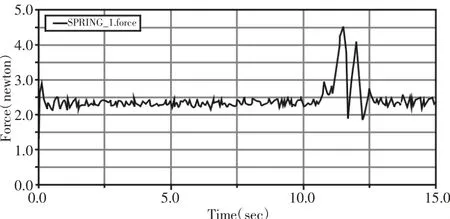
图9 正向越障下压簧的受力变化曲线Fig.9 The Force Change Curve of the Spring Under the Forward Obstacle

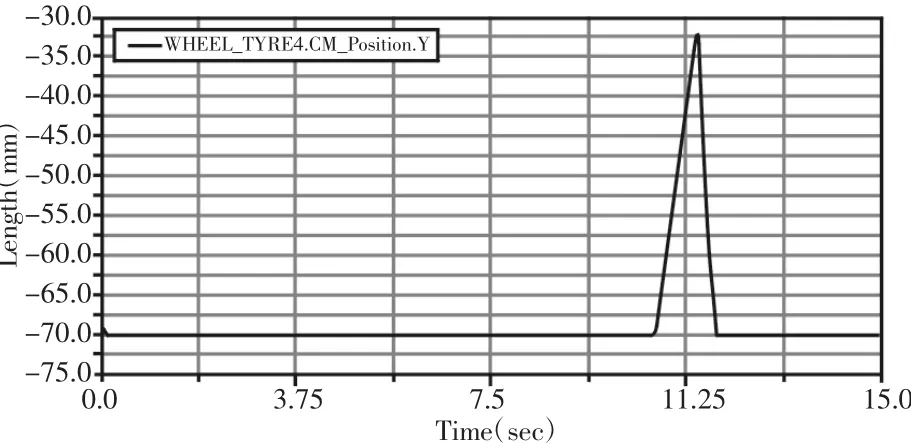
图10 正向越障下压缩位移变化曲线图Fig.10 The Compression Displacement’s Curve Under the Forward Obstacle

由图9 所示可知，当模拟管道检测机器人往正向方向越障时，碰到障碍物之前，在重力作用下，压簧会受到2.5N 左右的力，且一直保持在此范围上下浮动，浮动较小，浮动范围不超过0.5N，在10 秒以后，弹簧受到拉力，最大可达到4.5N 左右，浮动较大，越过障碍后，压簧所受力恢复为原来的状态。如图10 所示，随着时间的增加，管道检测机器人距离原点压缩位移保持不变，且在（10～12.5）s 之间，曲线有突变，可见在此时，管道检测机器人遇到高42mm 的障碍物，压缩位移先减小再增大，最后机器人顺利越过障碍。

从仿真分析结果来看，管道检测机器人能够正向通过比它自身轮子直径高2mm 的障碍物，且能正常行进。

4.2.2 反向越障仿真结果分析

机器人反向越障图，如图8（b）所示。轮子半径为20mm，假设障碍物为42mm 高，设置仿真时间为15s，步数为50。随着时间的增加，压簧受力情况，如图11 所示。机器人压缩位移变化曲线图，如图12 所示。

从图11 可以看出，开始仿真时，一开始由于受到重力的作用，压簧受到一定的冲击，随后压簧受力慢慢稳定在2.5N 附近，在第（10～12.5）s，压簧受力的变化幅度较大，可见，管道检测机器人在此时遇到了42mm 高的障碍物。由图12 可知，管道检测机器人开始运动时，随着时间的增加，机器人压缩位移先保持不变，同样也是在第（10～12.5）s 之间，曲线有很大波动，最后曲线趋于平稳，且变化趋势与图12 相符，由此可见在仿真中管道检测机器人顺利通过障碍物。

从仿真分析结果来看，管道检测机器人能够反向通过比它自身轮子直径高2mm 的障碍物，且能正常行进。

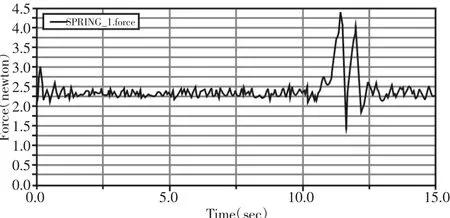
图11 反向越障下压簧的受力变化曲线Fig.11 The Force Variation Curve of the Lower Pressure Spring in Reverse

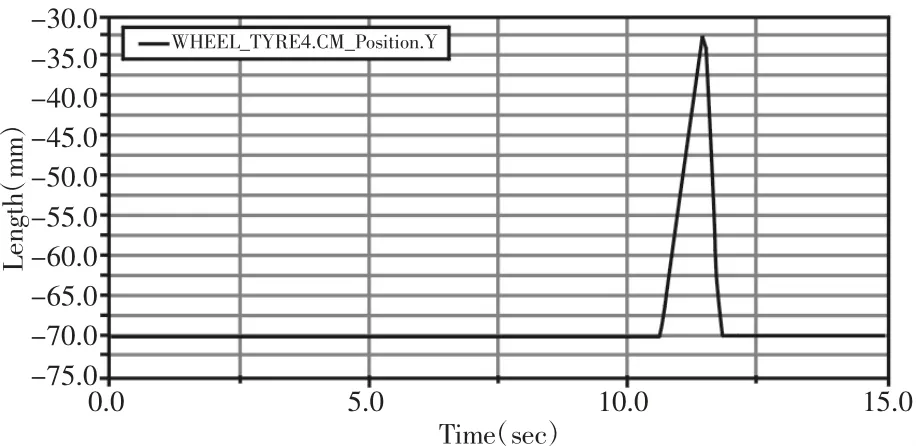
图12 反向越障下压缩位移变化曲线图Fig.12 The Curve of Compression Displacement in Reverse Direction

4.3 变径管道通过性仿真结果分析

管道检测机器人通过管道内径从240mm 变为180mm 的变径管道时[10]，机器人压缩位移曲线，如图13 所示。设置仿真步数为50 步，仿真时间为10s，驱动角速度为40°/s。

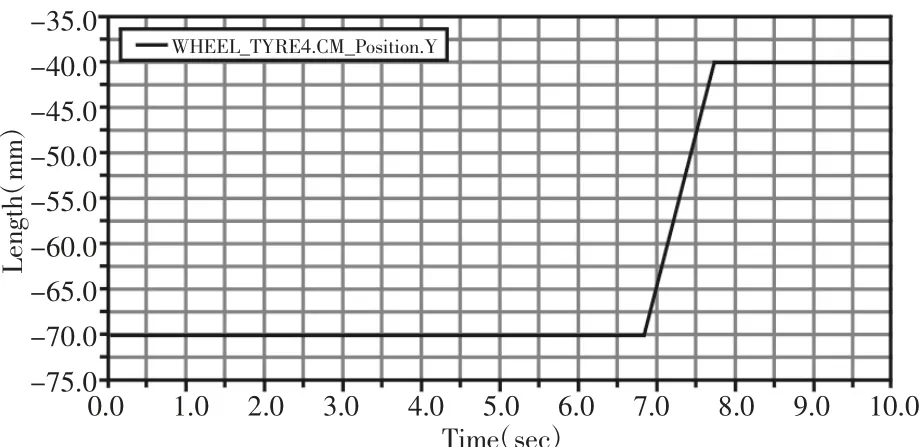
图13 机器人变径通过时压缩位移曲线图Fig.13 Compressive Displacement Curve of the Robot when it Passes Through

仿真时，因要使管道检测机器人通过管道的内径从240mm变为180mm，则需要将管道上下两端管壁各增加30mm 的厚度。由图13 所示，当管径逐渐变小时，可见轮心在压缩位移逐渐变小，当机器人处于管径为180mm 的时候，位移曲线趋于平衡，最后管道检测机器人顺利通过该变径管道。从仿真分析结果来看，管道检测机器人能顺利通过管径从（180～240）mm 的变径管道，这证实了该管道检测机器人的变径功能是可行的。

5 实验测试

经过上述仿真后，证明了管道检测机器人在复杂的管道环境下能实现变径功能和越障功能，变径功能和越障功能的实现能改善核工作环境下管道检测作业的难度。因此，我们对实物进行实验，进一步证明机器人具备良好的越障通过性和变径管道通过性。

5.1 机器人越障通过性测试

为了验证机器人在遇到障碍时具有通过性性能，设计并开展了如下实验，将管道检测机器人放置在四周设有高度为10mm障碍物的管道中，且障碍物连续出现2 次。如图14 所示，实验结果证明，该管道检测机器人能顺利通过障碍物，并能在连续越障两次后正常行进，由此可知，该机器人能连续2 次越过四周都设有10mm 高的障碍物，能够适应复杂的管道内部环境。

5.2 机器人变径管道通过性测试

为了验证机器人在遇到圆形变径管道时具有变径通过性，设计并开展了如下实验，将管道检测机器人放置在直径变化范围为220mm 至180mm 的圆形变径管道内行进，如图15 所示，实验结果证明，机器人能在直径为220mm 的管道内正常行进并能在圆形变径管道中顺利通过。因此，机器人本体机构能实现预期的变径作功能，具有通过变径管道的能力。

图14 机器人越障通过性测试图Fig.14 The Robot with the Obstacle Passing the Sex Test Graph

图15 机器人变径管道通过性测试图Fig.15 Test Diagram of Robot Variable Path Through Sex Test

6 结论

该管道检测机器人能够良好的解决双向越障问题，且能实现通过管道内径为（180～240）mm 范围内任两个尺寸的变换，同时上述设计的管道检测机器人也具备一定的弯管三通管通过能力。通过对该管道检测机器人进行三维建模及虚拟样机运动仿真，验证了设计的合理性及稳定性，表明该管道检测机器人完全符合设计指标。最后，通过对管道机器人的实物进行实验，进一步验证该机器人具有良好的越障通过性和变径管道通过性。