一道含有积分上限函数的不等式证明方法探讨

景慧丽,王兆强

(火箭军工程大学 基础部，陕西 西安 710025)

引言

不等式的证明是高等数学课程和数学分析课程的重要组成部分.不等式的证明没有固定模式，证明方法因题而异，灵活多变[1].另外，积分上限函数[2]是学员进入大学阶段学习接触到的一个新的函数类型，大部分学员遇到有关积分上限函数的题目就无从下手，没有思路.本文就某高校期末考试题中的一道含有积分上限函数的不等式的证明问题进行探讨，提出四种证明方法，进而培养学员的发散思维.

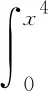
1 利用函数的单调性证明

则F′(x)=4x3-f(x4)·4x3=4x3[1-f(x4)]

由题意可知f(x4)<1，所以1-f(x4)>0.因此，当x>0时，F′(x)>0，所以F(x)在区间[0,+∞)上单调递增，故对∀x(0，+∞)，都有F(x)>F(0)；当x<0时，F′(x)<0，所以F(x)在区间(-∞,0]上单调递减，故对∀x(-∞,0)，都有F(x)>F(0).

2 利用函数的极值和最值证明

注3 利用函数的极值和最值证明不等式的一般步骤是：首先构造辅助函数F(x)，这里辅助函数的构造方法与利用函数的单调性证明不等式的辅助函数的构造方法一样；然后求出F(x)的驻点，即令F′(x)=0，解该方程即可；最后求出函数F(x)在给定区间上的最值，即可证得不等式[6].

注4 第二种证法尽管是利用函数的极小值和最小值来证明的，但其实质还是利用了函数的单调性.

3 利用定积分中值定理证明

因为函数f(t)在闭区间[0,x4]上连续，所以由定积分中值定理知：至少存在一点使ζ[0,x4]使得

4 利用定积分的性质证明

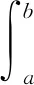
5 结语

以上就是该不等式的四种证明方法，比较这四种方法，最巧妙的是第三种证法，但学员用得最多的是第一种证法.由上述证明方法可以看出，一道题目往往可以用不同的方法、思路去求解，其知识点之间表面上看是相互独立的，实际上它们之间是具有一定联系的.另外，高等数学课程和数学分析课程中很多题目都可以用多种思路和方法来求解，如极限的计算、不定积分和定积分的计算、隐函数求导等等.在教学过程中，教员应根据教学内容，合理设计一些一题多解的题目，鼓励学员积极参与到教学活动中，鼓励学员敢于标新立异、勇于提出问题、开展交流和讨论，这样才有利于学员突破思维的局限性，培养学员的发散思维[1].