基于CFD/CSD耦合的全动平尾气动弹性特性研究
2020-10-21罗文莉陆琪
罗文莉,陆琪
(上海飞机设计研究院,上海 201210)
0 引言
对于多数常规飞行器建模,采用适当的刚体假设是合理的。但是对于相对厚度较小的活动面,如水平尾翼来说,很容易出现气动/结构耦合的现象,因此刚体假设是不可行的。尤其是随着飞行速度的不断增大,气动弹性的影响已不容忽视。因此,对于全动平尾的气动弹性研究是十分必要的。
关于气动弹性问题的研究从20世纪50年代开始兴起,由于计算能力的限制,那时的研究主要集中于风洞试验以及非定常气动理论。LAUTEN W T等[1]在气动弹性方面对X-15的全动水平尾翼缩比模型进行了风洞试验研究。基于活塞理论计算得到的颤振速度大约是试验得到速度的4倍。HEEG J等[2]对6种全动尾翼模型进行了风洞试验,主要针对翼型、翼轴刚度以及翼面质量分布进行了研究,全部试件的试验颤振速度均低于使用2阶活塞理论计算得到的值。
随着计算能力的不断提高,非定常气动力的计算方法逐渐由依靠理论分析转向了与CFD计算相结合的方法。MCNAMARA J J等[3-4]基于活塞理论、牛顿理论、激波膨胀波等非定常气动力方法计算了一种双楔形翼型的气弹稳定性,并与基于求解N-S方程的CFD方法进行了对比,结果表明使用1阶、2阶活塞理论的误差较大,并说明了黏性效应对于二维楔形薄翼型的影响基本可以忽略。
此后,集合了CFD流场分析和结构有限元计算(FEA)的CAE分析由于其在气弹分析中的先进性成为了一股研究趋势。MCNAMARA J J等[5]对X-33进行了气动弹性分析,使用MSC.NASTRAN进行模态分析。GUPTA K K等[6]分别采用了基于活塞理论、CFD以及系统识别等方法计算非定常气动力,结构采用有限元建模,得到的结果表明飞行器在工作环境中定常区域内不会发生颤振现象。
采用常规的理论算法或是基于CFD的非定常气动力算法无法考虑翼型的变形。对于结构模型的求解,国内外大多理论方法均假设结构在静变形平衡位置附近作小幅振动,采用线性结构振动方程,一些流固耦合降阶方法也是基于线性考虑[7]。然而近年来,国外很多学者提出了HISSS/NASTRAN、CFL3D/GFEC、ZAERO/NASTRAN等CFD/CSD(Computational Fluid Dynamics/Computational Structural Dynamics) 耦合方法,开始将其应用在常规亚/超飞行器气弹分析中。CFD采用精确的流动控制方程,CSD建立非线性结构模型,基于CFD/CSD耦合分析具有高精度,可用于复杂问题的研究。国内也有学者开展了相关研究,张华等[8]耦合FLUENT/NASTRAN,详细研究了机翼结构弹性对气动特性的影响,曾宪昂等[9]基于CFD/CSD耦合方法进行了某机翼的颤振分析。
1 计算方法
CFD/CSD耦合方法遵守基本守恒原则,在流体与固体耦合交界面处,满足流体与固体应力、位移、温度等变量的相等或守恒。通过分离解法分别求解流体和固体控制方程,再通过流固耦合交界面进行计算结果的传递。只要流固耦合面完全对应,可以保证交界面上的参数从局部到全局精确传递。由于各自的物理属性,在进行数据传递时,并不是所有的变量都要进行传递。流体将力传递给固体,固体将位移传递给流体。使用动网格模拟流场形状由于边界运动而随时间的改变,从而捕捉平尾的结构变形。
本文采用ANSYS软件,CFD计算基于有限体积法求解非定常雷诺平均N-S(RANS)方程。采用标准k-ε湍流模型结合壁面函数法,选择密度基隐式求解,对于空间离散方法,扩散项的无黏通量项选取AUSM通量差分分裂格式,而黏性通量项选取中心差分格式,对流项则使用2阶迎风格式。时间积分使用高斯赛德尔(gauss-seidel)方法。CSD计算基于有限元法,对固体结构进行离散,将连续结构的无限维问题转化为与节点位移相关联的有限维问题。固体运动方程可由拉格朗日方程得到:
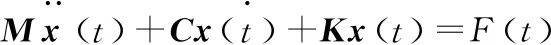
(1)
其中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;F为广义力;x为节点位移向量。
2 建模
2.1 气动模型
本文计算的全动平尾和坐标系定义如图1所示,z轴垂直于x轴和y轴,按右手定则给定正方向。翼根弦长6.309m,平尾宽度2.22m,翼型相对厚度0.04m,翼面积15.52m2。
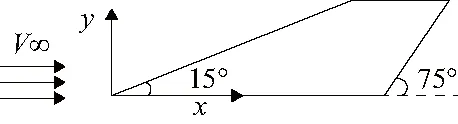
图1 平尾平面形状
计算域边界采用pressure far-field条件,高度为30 km,压力、温度等气体参数由标准大气表查得。对平尾周围流场进行网格划分,如图2所示。对称面上采用对称边界条件,且在动网格设置中,对称面设置为可变形面,将变形约束在面内。平尾上下表面、前后缘以及翼端面为设置流固耦合面,设置计算时间步长为0.001 s,最大迎角取40°。

图2 平尾附近流场网格划分
2.2 结构模型
采用直轴式全动平尾,即平尾与转轴组成整体相对垂直于机身的转轴旋转。将转轴位置定于翼根65%处,换算为平均气动弦长的43%。蒙皮厚度取2mm,翼轴长度取1m。翼轴选择TC4钛合金材料,翼面蒙皮为镍合金GH4169,平尾内部为全高度镍合金蜂窝结构。对平尾结构进行网格划分,如图3所示,网格数为28 000。其中翼根处翼轴末端面固定,翼根面变形约束在面内,平尾上下表面、前后缘以及翼端面设置为流固耦合面。同样设置时间步长为0.001 s。

图3 平尾结构网格
对平尾进行模态分析,得到前4阶模态如图4所示,其中黑色线框表示未变形的平尾,云图表示位移大小。各阶模态、频率见表1。
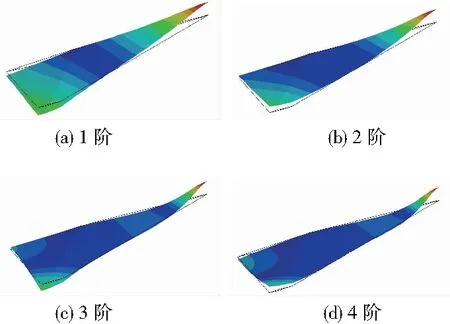
图4 平尾模态分析

表1 模态频率
3 气弹特性分析
3.1 气弹响应分析
分别计算平尾迎角为0°~40°间隔20°的情况,依次分析平尾的气动参数以及结构参数响应,其中气动参数包括升阻力系数,结构参数包括应力和平尾前缘点位移,初始值为不考虑结构弹性时的值。0°迎角时的气弹响应如图5所示。
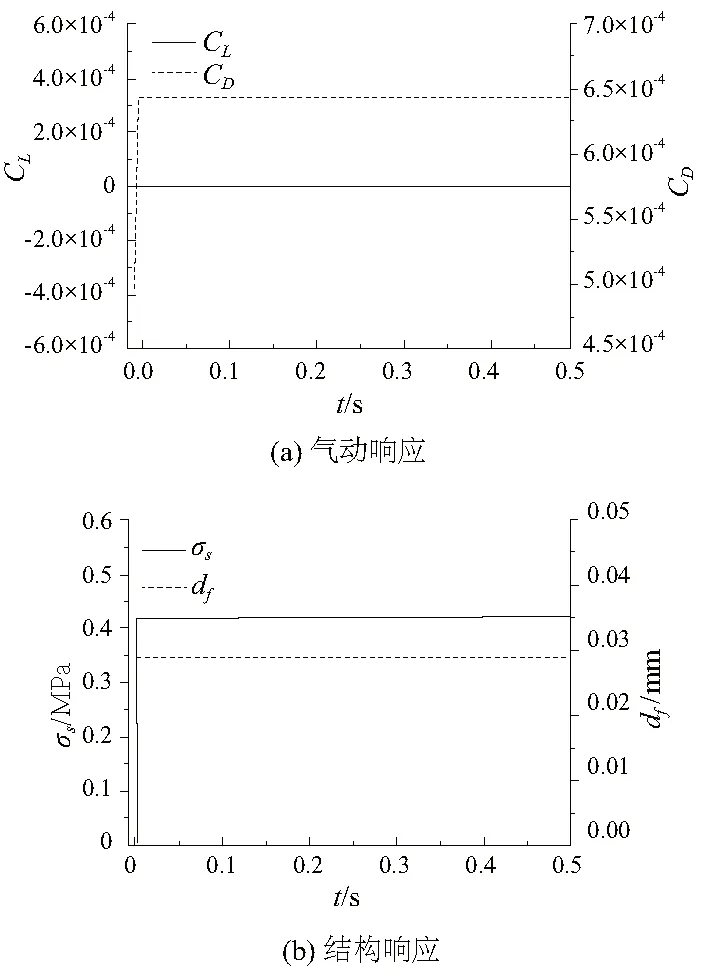
图5 0°迎角时的气弹响应
可以看出升阻力系数均很快收敛,并无明显波动。由于采用对称翼型,0°迎角下升力系数为0,阻力系数也仅在10-4量级。考虑结构弹性之后升力系数几乎不变,阻力系数增加30%,但幅值仍较小。结构响应结果同样可以看出,应力和位移两者均很快收敛稳定。其中最大应力值为0.42MPa,最大位移值为0.03mm,从量级上看,几乎可以忽略。
图6所示分别为20°和40°迎角下的气动响应结果。可以看出,升阻力系数均出现波动,无相位差且呈收敛趋势。20°迎角下升力系数初始值为0.282,收敛值约为0.272,减小约3.6%。阻力系数初始值为0.106,收敛值约为0.101,减小约4.7%。升阻力波动半衰时长约0.726 s。40°迎角下升力系数初始值为0.666,收敛值约为0.632,减小约5.1%。阻力系数初始值为0.563,收敛值约为0.526,减小约6.6%。升阻力波动半衰时长约0.478 s。
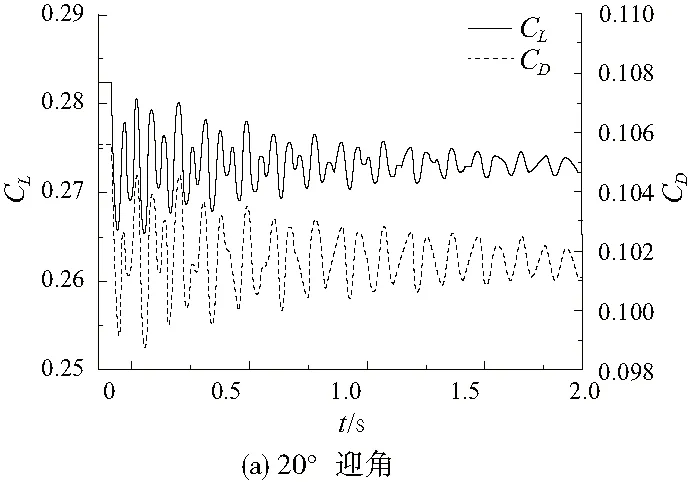
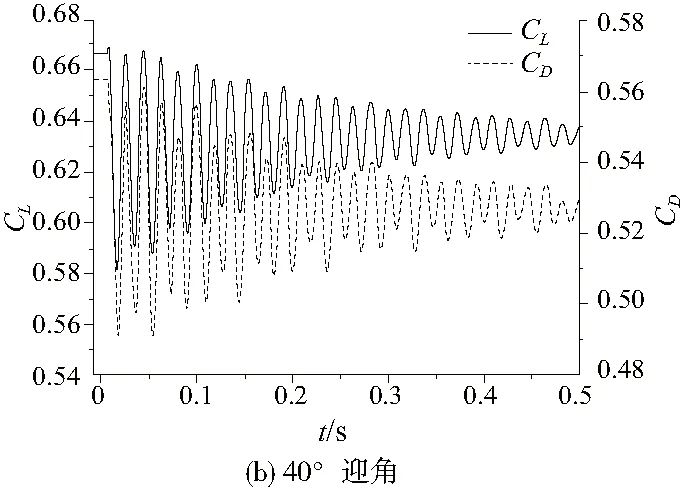
图6 大迎角下的气动响应
图7所示分别为20°和40°迎角下的结构响应结果。可以看出20°迎角下平尾前缘点位移最大值约120mm,且随时间逐渐衰减,收敛值约为60mm。在初始气动载荷的作用下,结构的应力响应曲线迅速达到最大值,约115MPa。此后随着时间的增长,响应逐渐衰减,最后收敛到约63MPa。40°迎角下位移最大值约330mm,且随时间逐渐衰减,收敛值约为97mm。在初始气动载荷的作用下,结构的应力响应曲线迅速达到最大值约320MPa,此后随着时间的增长,响应逐渐衰减,最后收敛到约190MPa。
可见除0°迎角迅速收敛至平衡位置以外,在大迎角下平尾的升阻力系数以及前缘点位移、翼轴最大应力点等效应力曲线均出现波动,随时间变化逐渐衰减至平衡位置。迎角越大,初始振幅越大,升阻力减小的比例越大,但衰减得越快。
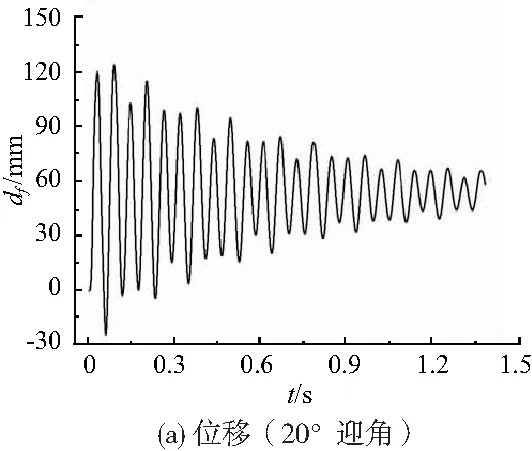
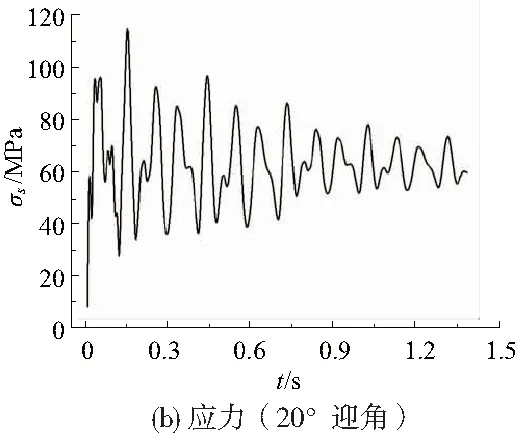
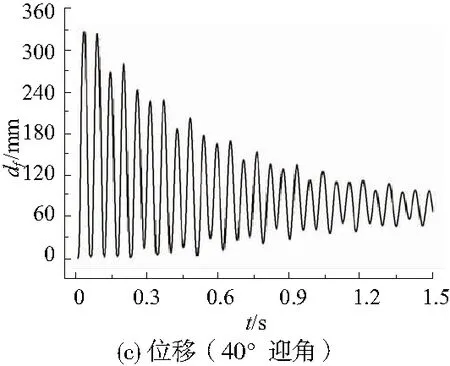
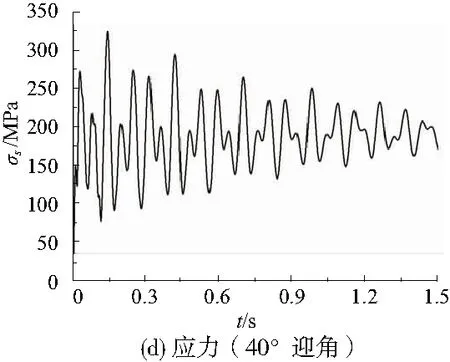
图7 大迎角下的结构响应
3.2 流动特性分析
图8所示为0°迎角下考虑结构弹性后翼根附近对称面以及平尾上、下表面的压力分布云图。可在0°迎角下上下表面的压力基本呈对称分布,因此升力系数几乎为0。
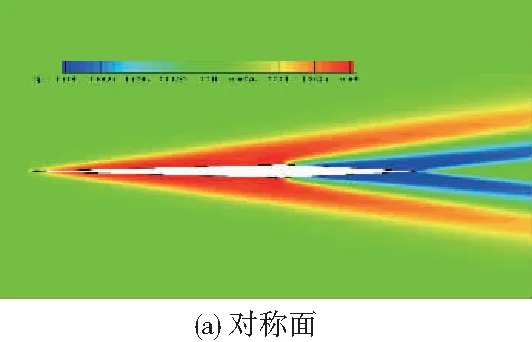
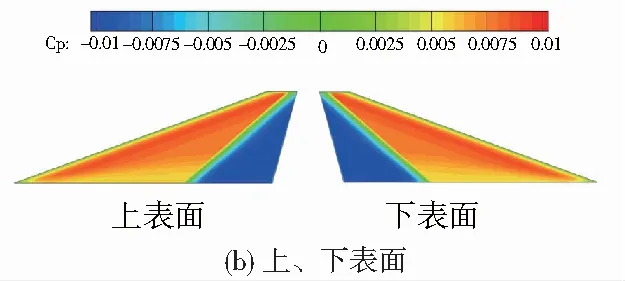
图8 压力分布云图(0°迎角)
图9所示为20°迎角时,初始流场与平衡位置所对应的平尾下表面压力分布云图以及平尾变形示意图。可以看出,结构变形导致下表面的压力分布发生变化。相比初始位置,平衡位置对应的平尾下表面后缘膨胀区低压区域扩大,平尾前缘高压区靠近前缘,使得翼尖处的高压区域明显缩小。
由平尾变形示意图可以看出,平衡时平尾发生扭转。从正视图可以看出50%展长以内的部分前缘向上偏转,相对迎角增大,从而使得激波偏折角增大,波后压力增大,因此造成高压区前移。而50%展长以外的部分前缘向下偏转,相对迎角减小,相应的激波后压力减小。从后视图可以看出平尾后缘均向上偏转,相对迎角增加,从而增大偏折角,但此时前方激波经过最大厚度处产生膨胀波,偏折角增大反而造成压力减小。综上,翼根前缘处压力的增大无法弥补翼尖前缘以及整个平尾后缘压力的降低,因此整体压力减小,升力系数降低。
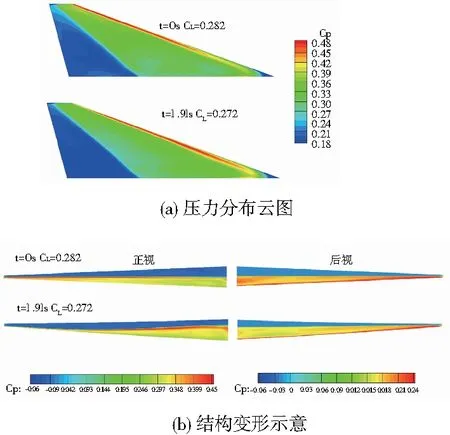
图9 结构变形后的流场(20°迎角)
图10给出了一个典型的振荡周期内平尾结构变形以及表面压力分布云图的变化过程。取0.03s~0.08s,间隔0.01s的6个时刻。可以明显看出平尾前缘扭转和翼尖弯曲变形。变形最大时升力系数最小,对应地,变形最小时升力系数最大。
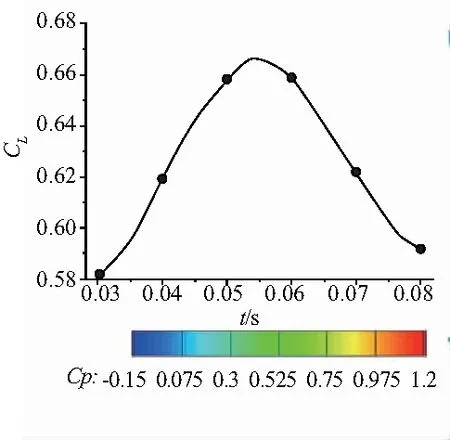
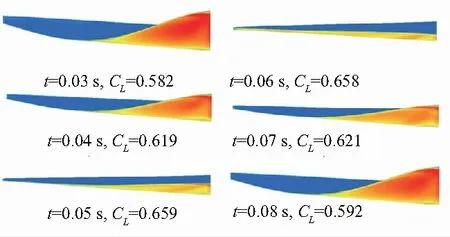
图10 平尾结构变形和表面压力分布云图
3.3 结构特性分析
图11所示为0°迎角时平尾的等效应力分布,可以看出,翼轴处应力分布较为集中,且应力最大出现在翼轴的x向与平尾相连接处。根据前文压力分布特点可以得出0°迎角下平尾结构受到的力主要是阻力,集中在x轴方向,而在z向由于上、下表面对称升力为0,因此应力较小。
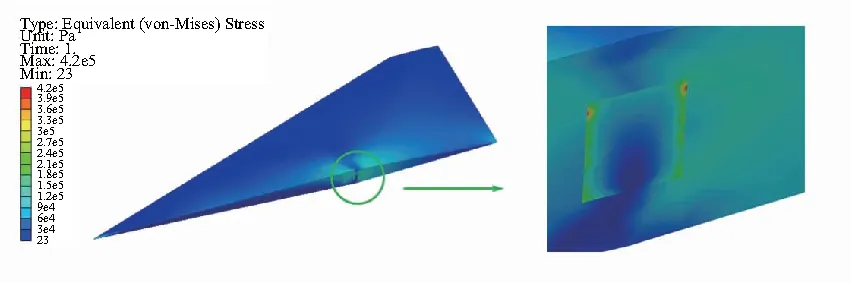
图11 结构应力(0°迎角)
图12为20°和40°迎角下变形最大时对应的等效应力分布云图,可以看出,靠近翼轴处应力较为集中,而翼轴上的应力较小。迎角越大,最大应力越大。平尾内部最大应力在40°时达到1.9 GPa,已经达到所用镍合金材料的
屈服强度极限,理论上说材料已经破坏,由于采用线弹性材料,计算结果可能较实际结果偏大,但为了保险起见,实际结构设计时应在翼轴与内部蜂窝接触部位附近加固,防止蜂窝结构破坏。
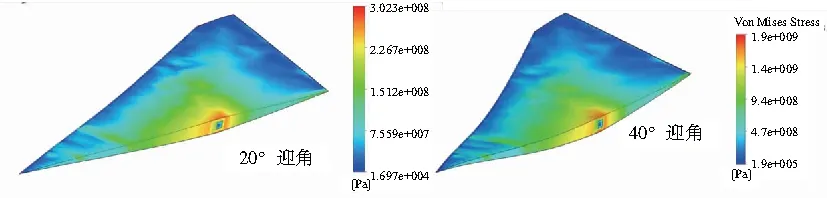
图12 大迎角下的等效应力分布云图
4 结语
本文采用CFD/CSD流固耦合法对一种典型全动平尾进行了气动弹性数值模拟。给出了不同迎角下平尾的气动弹性响应,并分别针对流场和结构响应做出了分析,结果表明:
1) 除0°迎角迅速收敛至平衡位置以外,其余各迎角时的气动力和结构响应曲线均出现波动,随时间变化逐渐衰减至平衡位置。迎角越大,初始振幅越大,气动力减小的比例越大,结构应力越大,但随时间衰减得越快。
2) 结构变形导致下表面压力分布发生变化。靠近翼根部分前缘上偏,压力增大。靠近翼尖部分前缘下偏,压力减小。后缘均上偏,压力减小。整体压力减小,升力系数降低。迎角越大,现象越明显。
3) 靠近翼轴处应力较为集中,而翼轴上的应力较小。平尾存在弯曲/扭转耦合现象,随时间逐渐收敛至平衡位
置,但相对初始位置的变形随迎角增大而增大。
