基于图论的雷达优化部署方法
2020-10-21孙华飞张世强何孟源陈静超李萌萌曹越琦
孙华飞, 张世强, 何孟源, 陈静超, 李萌萌, 曹越琦
(1. 北京理工大学 数学与统计学院, 北京 100081; 2. 中国航天系统科学与工程研究院,北京 100048)
现代空域环境日趋复杂,空袭是非常重要的防御目标之一. 空袭目标可能来自不同高度层,单部雷达显然不能满足多高度层覆盖的需要,需要部署多部雷达协同作战.雷达组网的作战效能很大程度上取决于组网部署,部署方案将直接影响空域情报信息的收集. 因此,雷达组网的优化部署问题是现代空域防御的关键研究问题之一. 雷达网优化部署的优劣直接影响传感器时间覆盖、空间覆盖、目标数据率,同时影响传感器的抗干扰能力、反隐身能力以及生存能力,最终影响整个雷达组网的作战性能.
在雷达组网优化部署的问题中,已有许多研究工作,最为广泛的方法是蒙特卡罗方法[1]和遗传算法[2-5]以及一系列改进的自适应遗传算法[6]等经典方法. 蒙特卡罗方法是在限定组网部署形式时的常用方法,编程简单便于实现,而且在计算雷达组网的联合探测面积时非常便利. 但这显然限制了雷达部署形式,在实际应用中缺乏灵活性,不利于实时应变. 而遗传算法及其一系列改进方法在解决该问题时,对部署形式有很好的适应性,打破部署形式的限制,且雷达数目较多时,可以并行处理,容易编程实现,且具有很强的自适应性. 以上传统的优化算法易于理解,便于实现,但当组网中雷达数目较多时,计算量大大增加,无法在一个较短时间内给出最佳部署方案,并且战争环境的复杂性决定了雷达组网部署时约束的多样性,以上两种方法不够灵活,不易于不同约束条件的嫁接.所以,针对传统方法在雷达部署问题中存在的不足,本文基于图论理论[7-8]设计了计算量小、运行速度快,对不同约束条件都能够很好地兼容的算法.
本文对雷达的探测区域以及雷达的位置离散化后转化为点,根据雷达的探测概率函数[9]等指标建图,利用图论相关知识将雷达部署问题转化为一个图论问题. 之后根据不同的约束条件建立相关模型并设计对应的算法求解,最后给出模拟仿真.
1 预备知识
1.1 图论相关知识[10]
定义1.1.1一个无向图G是一个有序的二元组,记为G=〈V,E〉,其中
①V是一个非空有序集,称为顶点集,其元素称为顶点或节点.
②E是无序集{{a,b}|a,b∈V}的有穷多重子集,称为边集,其元素称为无向边.
定义1.1.2无重边无自环的图称为简单图.
定义1.1.3设无向简单图G=〈V,E〉,V*⊆V,若∀vi∈V-V*,∃vj∈V*使得(vi,vj)∈E,则称V*为G的一个支配集,并称vj支配vi.
定义1.1.4设无向简单图G=〈V,E〉,V*⊆V,若V*中任意两个顶点不相邻,则称V*为G的一个点独立集,简称独立集.
定义1.1.5设无向简单图G=〈V,E〉,V*⊆V,若∀e∈E,∃v∈V*,使得v与e相关联,则称V*为G的点覆盖集,简称点覆盖,并称v覆盖e.
定义1.1.6设无向图G=〈V,E〉,若能将V划分成V1和V2(即V1∪V2=V,V1∩V2=∅,V1,V2≠∅),使得G中每条边的两个端点都是一个属于V1,另一个属于V2,则称G为二部图(或二分图),称V1和V2为互补顶点子集,常将二分图G记为G=〈V1,V2,E〉.
1.2 雷达部署相关知识
在雷达部署问题中,通常侧重某一高度的覆盖问题,也即覆盖区域是二维平面的一个连通子集. 在考虑覆盖问题之前,首先要知道一部雷达的覆盖区域,这就涉及到雷达的探测概率函数以及雷达的俯仰角.
雷达的探测概率函数是一个与雷达参数以及目标距雷达距离相关的函数,在雷达确定的前提下,雷达探测概率函数只依赖于目标距雷达的距离,且随距离增大探测概率单调递减. 由于不同种类的雷达探测概率函数不同,且探测概率函数形式较为复杂,在实际应用过程中直接用探测概率函数会极大地增加计算的复杂度,故通常设定一个可探测的概率界限,根据该概率界限得到雷达的探测范围,只要目标在该探测范围内即视为该目标可探测,显然雷达的探测范围为一个圆.

雷达的俯仰角是对探测目标与雷达连线和水平平面夹角的限制,超出该限制的目标雷达是无法探测的,这与距离无关,只有满足该限制时才能利用雷达探测概率函数判定是否可探测,这就是雷达探测盲区的由来.

注1.2.1在之后的讨论中,不再具体分析探测概率函数和俯仰角,直接用内外半径分别为r和R来表示该雷达的圆环形探测区域.
在知道雷达的探测区域后,首先考虑的因素是对该区域的覆盖率,即被覆盖区域面积与整个区域面积的比值. 通常需要部署的雷达对整个区域全覆盖,由于雷达顶端盲区(即圆环中间的空心圆)的存在,雷达重复覆盖面积很大,这种冗余会造成雷达资源浪费,故实际考虑时需要控制冗余,使其面积不能过大.
定义1.2.3(冗余度)设整个区域面积为S,被覆盖k次及以上的区域视作冗余,若某雷达部署方案的冗余面积为T,那么定义该方案的冗余度为T/S.
在之前的分析中是将整个区域不加区分,一个雷达探测范围内的区域均视作可探测,但实际中可能需要对一些区域重点探测,此时需要雷达联合探测机制,即一块区域需要多部雷达一起探测,这些区域称作重点区域.
2 雷达部署
首先通过离散化后建图将雷达部署问题转化为图论相关问题,介绍状态压缩的概念,并在离散化后的问题上重新定义覆盖率、冗余度等约束条件,之后根据考虑因素的增多将雷达部署问题分成4个子问题,从最平凡的固定高度用同一种雷达不考虑重点区域的覆盖问题入手,逐渐深化问题,最终对于不同高度用多用雷达考虑重点区域的覆盖问题建立模型并设计相关算法,在模拟仿真中可以看出该算法对于这几个子问题均可给出很好的部署方案.
2.1 离散化
在实际应用中,由于需要覆盖的区域的点数无限,雷达位置也有无限种可能,故直接考虑该问题是十分困难的. 但如果把责任区域离散化为若干小区域(例如网格化),只要每个区域的面积相对于整个区域以及雷达的扫描区域充分小,那么一个区域的覆盖问题近似于对该区域中心点的覆盖问题. 而对于雷达的位置,由于实际情况下一些区域无法安装雷达,不妨取一些合适安装雷达的点作为初始雷达的位置,那么问题转化为从这些初始位置中选取一个子集作为所选雷达集合,选取的该集合需要满足一定约束条件.
假设区域离散化后有n个小区域,进而得到这n个小区域的n个中心点,初始选取雷达位置有m个,根据每个位置雷达的圆环形探测范围可以求出每部雷达可以探测到的中心点集,根据可探测关系建图,可以得到一个二分图如图1所示,那么全覆盖问题即为从雷达点集中选取子集使得区域点集中任一点都与该子集中某点相关联,而冗余度等限制则是对所选点集的一种约束.
2.2 状态压缩
状态压缩方法是算法设计中常用的手段,该方法是用一个状态压缩值来表示一种将固定点集中每点分类的方案,且从一个状态压缩值可以很快地得到具体方案. 在本问题中,由图论理论把警戒区域以及雷达位置均进行离散化,从而区域和雷达位置分别由两个独立点集表示,而每个位置是否放雷达、放何种雷达即为对该位置分类,以此为基础,应用状态压缩方法可以将每种雷达部署方案数值化,极大地方便了数值求解.
此处首先给出状态压缩方法最初始的定义,即先不考虑点集中点的分类,只考虑每点选或不选(或从点集中选出子集)的方案与状态压缩值的一一对应.
定义2.2.1(状态压缩)对于一个有n个元素a0,a1,…,an-1的集合T的一个子集T′,定义T′的状态压缩值为
(1)
式中:xi=0表示T′中没有元素ai;xi=1表示T′中有元素ai,进而建立了T的子集T′与一个介于0~2n-1之间整数的一一对应.
2.3 约束条件重新定义
定义2.3.1(覆盖率)假设有n个中心点,某个雷达部署方案覆盖了其中的n′个中心点,那么该方案的覆盖率为n′/n.
定义2.3.2(冗余度)假设有n个中心点,一个中心点被覆盖k次视作冗余,某个雷达部署方案让n′个中心点冗余,那么该方案的冗余度为n′/n.
2.4 固定高度用一种雷达不考虑重点区域的覆盖问题
假设有n个中心点,m个雷达位置集合,给m个雷达编号0,1,…,m-1,对于雷达集合T的一个子集T′,用其状态压缩值Sta(T′)表示,如此状态压缩将子集的概念数值化,进而极大地方便了存储和计算. 此时不考虑重点区域,故先不考虑联合探测. 本部分要解决的问题即为在全覆盖的前提下如何使冗余度最小.
2.5 固定高度用一种雷达考虑重点区域的覆盖问题
当所给区域中有一些重点区域,也即需要多部雷达覆盖的区域时,此时需要考虑联合探测,而之前的状态压缩理论依旧有效,但此时很大的变化是覆盖的重新定义. 可以通过概率函数得到每个中心点被覆盖需要的雷达部数(直观上可以看做多个圆环的相交部分为重点区域),注意到概率函数的不同会影响每一点需要被覆盖的次数,记zi为第i个中心点需要被覆盖的次数. 本文要解决的问题依旧是在全覆盖的前提下如何使冗余度最小.
2.6 固定高度用多种雷达考虑重点区域的覆盖问题
2.6.1问题分析
该问题比之前二个问题的变化为要在选定雷达位置集合的基础上还要给每个位置的雷达赋予对应的种类,故要对之前的状态压缩进行一些改变. 假设第i个位置的雷达有cnti-1个种类可以选取,分别为ai,1,…,ai,cnti-1,那么第i个位置的雷达有cnti种情况,不放置雷达或放置这cnti-1种雷达之一,故有以下进阶的状态压缩.
定义2.6.1(状态压缩)对于一个有n个元素a0,…,an-1的集合T,假设ai有cnti-1种分配方案,那么定义从T中选取若干元素并分别分配好的方案T′的状态压缩值为
cnt0cnt1x2+…+cnt0cnt1…cntn-1xn-1.
(2)

2.6.2预备工作
根据一个方案的状态压缩值需要得到该方案的具体安排,对于之前的二进制状态压缩,可以通过逻辑运算快速得到状态压缩值的具体含义,而此时的状态压缩发生了较大改变,故需重新给出一种新的求具体方案的方法.
对于方案S,已知其状态压缩值Sta(S),欲求x0,x1,…,xn-1,首先可以看出
x0=Sta(S)%cnt0.
(3)
之后把x0从Sta(S)中减掉,那么有
(4)
以此类推有
(5)
进而可以在线性复杂度内求出x0,x1,…,xn-1.
2.6.3模型建立
① 初始参数.
将区域离散化为n个中心点,设其坐标为(xi,yi),需要被覆盖的次数为zi(0≤i 设初始雷达位置有m个,设其坐标为(Xi,Yi),0≤i 设有N种雷达,其扫描区域的内外半径为ri,Ri,0≤i 设第i个雷达位置可选雷达种类有cnti-1种,种类分别为ci,1,…,ci,cnti-1,0≤i 一个中心点覆盖次数不低于k次视作冗余. ② 目标函数. 对于给定的方案状态压缩值,线性时间得到每个位置放置的雷达种类,根据雷达的扫描概率函数得到每个点被覆盖需要的雷达部数zi,根据所放置雷达的扫描范围得到当前雷达集合对第i个点的覆盖次数为ZT(i),那么ZT(i)≥zi时第i个中心点被覆盖,而ZT(i)≥k则视作该中心点冗余覆盖,设waste(T)表示冗余点的个数,雷达集合T中的雷达个数为num(T),那么目标函数及限制即为 (6) 2.6.4算法设计 第1步 离散化得到n个需要被覆盖的点的坐标(xi,yi),m个雷达的坐标(Xi,Yi),通过每点位置和每个雷达的探测概率函数得到每个中心点需要被覆盖的次数zi; 第2步 预处理mark(i),即对于第i个目标点,求出第j个雷达到第i个目标点的距离,如果该距离位于该雷达的圆环扫描范围内则将j加入mark(i)中; 第3步 通过雷达的扫描概率函数以其俯仰角得到每种雷达在给定高度的圆环形扫描区域的内外半径ri,Ri,0≤i 第4步 初始化选取雷达最小数量ans=m表示选取所有雷达必然满足条件,并计算出此时冗余点个数ansk; 2.6.5复杂度分析 在考虑多种高度时,显然高空的覆盖范围是低空覆盖范围的收缩,若考虑对整个空域全覆盖那么本质上是对高空全覆盖,问题变成固定高度用多种雷达考虑重点区域的覆盖问题. 故此处可以考虑对不同高度设置权重,使得最终加权覆盖率达到所给限制的覆盖问题,而该问题本质上是对第3部分结果的加权,此处不再重复之前的模型建立和算法设计. 给定高度的平面上[0,1 000]km×[400,1 200]km的矩形区域. 考虑到雷达的扫描半径,将该区域划分成20×20的小块,每块区域用其中心点代替,进而将该区域离散化成n=2 000个点,设其坐标为(xi,yi),0≤i 设定m=20个初始雷达坐标,其横坐标分别为100,300,500,700,900,纵坐标分别为500,700,900,1 100,记其坐标分别为(Xi,Yi),0≤i 假设雷达在该高度扫描区域外半径为330 km,内半径为30 km,结果如图4,选取了7个雷达,最小冗余度为16.44%. 如图5所示,划定一块由6个顶点的凸多边形为重点区域,分别考虑不同扫描半径的雷达对该区域的覆盖情况. 假设雷达在该高度扫描区域外半径为330 km,内半径为30 km,结果如图6,选取了7个雷达,最小冗余度为16.35%. 同样考虑之前的区域,此时不再分别考虑不同扫描半径的雷达对该区域的覆盖情况,而是考虑用多种雷达对该区域进行全覆盖. 假设雷达有7种,其扫描半径和俯仰角分别为(单位:(km,(°)): (330,5~55),(170,8~52),(280,6~56), (230,5~55),(360,10~50),(140,8~48), (260,12~55). 在10 km高度考虑这7种雷达对整个区域的覆盖,选取m=12个位置为雷达初始位置,其横坐标分别为125,375,625,875,纵坐标分别为500,800,1 100. 根据不同位置所选雷达种类的不同,此处给出两个运行结果如下. 第1种方案:如图7所示,选取了8个雷达,冗余度为12.50%,其位置和半径分别为 ((125,500),330),((125,1 100),330), ((375,500),280),((375,1 100),360), ((625,500),330),((875,500),170), ((875,800),330),((875,1 100),280). 第2种方案:如图8所示,选取了8个雷达,冗余度为14.70%,其位置和半径分别为 ((125,500),230),((125,800),360), ((125,1 100),330),((625,500),330), ((625,800),280),((625,1 100),230), ((875,500),280),((875,1 100),360). 从模拟仿真结果可以看出,在无重点区域时,本算法给出的部署方案一方面保证了对整个区域全覆盖,另一方面让冗余度尽可能小,避免了资源浪费. 而在有重点区域时,雷达覆盖会以该重点区域为重心,对该区域重点覆盖,同时也能够保证对冗余度的限制. 而在最后用多种雷达覆盖该区域时,根据所给雷达的种类以及每个位置适合放置雷达种类的不同,本算法均可快速给出对应的部署方案,达到了多种雷达共同探测、全覆盖、所用雷达代价最小、重点区域重点覆盖、冗余度满足约束等目标. 将图论理论和状态压缩应用到雷达部署问题中,提出了新的雷达组网部署方法,在理论上突破了传统优化方法的研究思路. 该方法能够灵活处理不同约束条件对雷达组网优化部署的限制,具有很强的兼容性. 同时,与传统优化方法相比,本文所提方法计算量较低,大大节省了计算时间,提升优化部署效率,便于实时战略调整.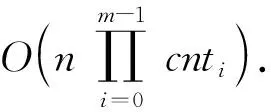
2.7 多种高度用多种雷达考虑重点区域的覆盖问题
3 模拟仿真
3.1 固定高度用一种雷达不考虑重点区域的覆盖问题
3.2 固定高度用一种雷达考虑重点区域的覆盖问题
3.3 固定高度用多种雷达考虑重点区域的覆盖问题
3.4 结果分析
4 结 论
