基于驱动电机控制的电动汽车坡道静止保持系统

李贵强， 吴正斌， 姜帆， 林祥辉， 武利强

(1. 中国科学院大学 深圳先进技术研究院，深圳,广东 518055; 2. 天津中科先进技术研究院有限公司，天津 300392;3. 河北工业大学，省部共建电工装备可靠性与智能化国家重点实验室，天津 300132; 4. 北京科瑞远腾测控技术有限公司，北京 100191)

坡道辅助起动技术可以实现坡道行驶过程中的静止保持功能. 制动器产生的驻车制动力使车辆临时停在坡道上，车辆起动时,一旦驱动力大于坡道阻力，驻车制动自动释放,从而使汽车平稳起步[1-2]. 坡道静止保持能够防止汽车后移，对于车辆坡道行驶安全至关重要. 虽然车辆坡道静止可以通过电子驻车制动系统实现，控制系统的研究已经相对成熟，但在坡道起步时，油门和制动器控制不当，存在冲击或车辆后移等安全隐患. 另外，为充分发挥电动汽车动力源的特点, 可以重新设计其坡道静止控制系统.

现有的坡道辅助起动技术重点在于驱动系统与制动系统的控制匹配，涉及较多的传感器和复杂的算法. 初亮等[3]验证了集成式电子驻车系统起步控制策略正确性. 王洪亮等[4]讨论了EPB系统实现汽车坡道起步自动控制的可行，提出基于角度传感器的坡道阻力计算方法，设计了坡道起步过程中驱动力与驻车制动力的协调控制策略. 使用PID 控制方法解决坡道起步过程中的驻车制动力释放滞后问题[5]. 在分析坡道起步的受力模型以及气压式EPB 工作原理基础上，采用Bang-Bang控制策略，实现坡道起步需求气压理想控制目标[6]. 在建立坡道起步的 EPB 气压控制模型基础上，提出使用逻辑门限实现控制目标[7]. 从以上研究可以看出，目前稳定的坡道静止保持状态还是需要依靠控制制动系统来实现. 且坡道和车辆载荷的变化会引起坡道阻力的变化, 增加了精确调节制动力难度.

为解决上述问题,文中提出一种使用驱动电机实现电动汽车坡道静止方法. 电动汽车(EV)通常采用永磁同步电机驱动行驶，对环境影响相对内燃机汽车较小，是汽车工业未来发展方向[8]. 磁场定向控制(FOC)技术不断发展，能够实现电机转矩的快速精准控制，保证输出转矩与车辆行驶阻力的匹配，采用控制驱动电机实现坡道静止保持成为可能. 吴兵显等[9]研究了电动汽车坡道起步控制策略，提出了驱动电机和制动器协调配合的自适应起步控制方法. 另外，永磁同步电机具有高阶、强耦合特性，且动态品质受电机参数变化及扰动影响明显[10]，采用电机驱动实现车辆坡道静止保持(MSH)则不仅需要考虑驱动电机扰动，而且需要考虑整车质量等参数以及坡度等外部条件参数的不确定性. 所以，MSH控制策略既要抗扰，又要不依赖精确的数学模型.

自抗扰控制技术是一种以主动抗扰、对系统模型依赖小的控制方法. 自抗扰控制以扩张状态观测器为核心,将外部扰动和模型差异统称为总扰动, 通过扩张状态观测器实时估计,由反馈控制律消除. 使得影响输出的扰动还未发挥作用时, 即被估计和补偿, 因此，增强了系统的鲁棒性. 并且，随着线性自抗扰控制的提出[11],降低了调参的工作时间,促进了自抗扰控制技术的研究与应用. 与其他控制方法相比,自抗扰控制具有主动抗扰和良好的控制性能，获得广泛关注, 且已在多个工程领域成功应用，均取得良好效果[12-14].

文中采用“辨识自抗扰”控制方法实现MSH系统控制. 基于电机控制系统的已知参数，本研究利用变遗忘因子最小二乘法算法对车辆质量和道路坡度进行辨识；通过建立MSH纵向运动学模型，根据自抗扰理论，搭建了自抗扰控制器，并进行系统稳定性分析，最后对文中所提方法进行了实车验证.

1 MSH动力学模型

1.1 永磁同步电机模型分析

图1为永磁同步电机(permanent magnet synchronous motor, PMSM)等效d-q模型.

采用id=0矢量控制策略，电流环模型为

(1)

式中:ud和uq分别为定子电压的d-q轴分量；id为定子电流的d轴分量;iq为定子电流q轴分量；R为定子的电阻;pn为电机极对数;λm为永磁体磁链；Ld和Lq分别为d-q轴电感分量；wd和wq分别为d,q轴系统的总扰动，b0d和b0q为电流环控制增益.

由于电机在运行过程中，随着负载变化，其交直轴电感，定子电阻存在非线性变化，所以建立电机精确数学模型非常困难. 因ESO扩展一阶作为干扰的观测参数，即外界负载等变化扰动和内部电机参数未建模非线性变化统称为总扰动. 使用ESO对总扰动进行观测估计，经过调节控制率和控制增益，使得总扰动还未发挥作用时, 即被估计和补偿，从而使系统达到期望的转速或转角. 因此，ESO既可以简化电机参数的建模，又能提高控制系统对扰动的鲁棒性能.

1.2 车辆动力学模型分析

电动汽车坡道受力情况如图2所示. 路面坡度角为γ，车辆在斜坡上纵向受力分别为驱动力Fb、滚动阻力Ff、空气阻力Fk及坡道阻力Fg. 坡道阻力作用下车辆会后移，若不采取制动措施车辆会出现极其危险的加速溜坡现象. 车辆使用制动系统的摩擦力抵消车辆坡道阻力，使得车辆静止于坡道. 电动汽车采用电机为驱动源，如果通过调整电机输出电磁转矩，控制驱动力匹配坡道阻力, 就能实现车在坡道静止功能. 而且，电动汽车坡道起步，只需在上述电磁转矩上叠加起步的增量，就能平稳起步，避免了因制动系统释放延迟或提前引起坡道起步冲击和后移等问题.

根据牛顿第二定律，建立车辆纵向动力学方程

ma=Fb-(Fg+Fk+Ff),

(2)

式中:m为车辆总质量，由车辆质量mv和乘客质量me构成;a为车辆加速度(沿斜坡向上为正). 制动过程中Fb应大于Fg-Ff-Fk, 使下滑加速度为负值, 直至车辆速度v稳定为0. 制动力由电机提供, 表达式为

Fb(iq,x)=Tei0η/(rx),

(3)

式中:Te为电机输出转矩;r为车轮半径;i0为减速器传动比;x为车辆后移距离；η为传动效率.

根据式(2)和(3)，可写为

(4)

式中:ρ为空气密度,kg/m2;Cd为空气阻力系数;A为车辆的迎风面积,m2;Ad为滚动阻力系数;v为车辆速度;g为重力加速度.

假设:车速变化较小，不计空气阻力和滚动阻力;道路坡道角γ足够小,取sinγ=γ. 则车辆静止稳定后，驱动力与道路坡道角近似呈正比:

Fb≈mgγ=(mv+me)gγ.

(5)

综上，在车辆稳定静止点x0，可得出坡道静止系统模型：

(6)

对驱动力进行傅里叶分析，舍去高阶项，可得到如下公式

(7)

根据式(6)和(7)，MSH系统方程平衡点模型为

(8)

式中：iq为输入变量;x为输出变量.式(8)进行拉氏变换，整理可得系统传递函数

(9)

由式(5)(6)和(9)可知，道路坡道角以三角函数形式约束坡道阻力和滚动阻力,对驱动力有非线性影响; 此外,坡道起伏还会引起道路坡道角变化,形成外部扰动. 因此,MSH系统具有外部扰动的后移距离x的二阶系统. 文中主要考虑了坡道静止系统中主要的两种干扰:一是由电机运行过程中，电机参数非线性变化引起的未知扰动,二是实际工况中车辆质量和道路坡道造成的系统输入不确定性. 在正常工况下，车辆质量已知，受载荷约束，乘客质量变化是有界的,此外,道路坡度在实际中也是有界的.

2 坡道和车辆质量参数辨识

最小二乘算法简洁，不仅适于静态系统参数估算，带遗忘因子的递推最小二乘算法也可以应用于动态系统参数估算[15].

2.1 变遗忘因子最小二乘算法估计

文中利用变遗忘因子最小二乘方法对路面坡度和质量问题进行估计[16]，系统模型如图3所示.

其中：x(k)为系统输入序列;y(k)为系统输出序列;z(k)为输出测量值;θ(k)为系统待辨识参数序列;w(k)为系统噪声量. 即：

z(k)=xT(k)θ(k)+w(k),

(10)

(11)

基本最小二乘法对整车质量和路面坡度辨识时，随着采集数据的增多，新数据提供的信息将被旧数据淹没，算法慢慢就会失去修正能力. 同时，由于质量和坡度不稳定，固定的遗忘因子不能获得系统准确的动态特征.

因此，采用变遗忘因子最小二乘算法，对车辆质量和路面坡度进行实时跟踪，每获得一次新的观测数据就修正一次参数估计值，随车况和路况的变化进行自适应调节，获得更好的动态响应.

为优化最小二乘法，引入变遗忘因子τ，0<τ<1，即引入了一个加权矩阵，避免随着修正值的增加，系统的输入输出对参数估计的修正能力降低的问题. 带遗忘因子最小二乘法辨识算法表达式如下

(12)

式中:K(k)为其增益矩阵;P(k)为系统协方差矩阵;I为单位矩阵;遗忘因子τ取值范围一般为0.9≤τ≤1.0. 在基于变遗忘因子最小二乘算法的车辆质量和道路坡度进行辨识过程中，算法实现的关键在于如何得到车况和路况为未知的矢量线性方程.

2.2 整车质量和道路坡度辨识

采用变遗忘因子最小二乘法，考虑随时可能变化的整车质量，以及相关汽车行驶的动力学系统特性变化，能实时辨识整车质量，同时也能确保路面坡度识别的准确性.

根据车辆坡道行驶纵向动力学模型，传动效率取1，得整车加速度[16]

(13)

由式(7)和式(10)，将式(13)整理成最小二乘格式为

(14)

式中:x(k)为车辆行驶过程中系统样本序列;iq为电机驱动电流，车速由电机转速测得;θ(k)为系统待辨识的车辆质量和道路坡度序列.

若为后桥驱动，前轮因不存在驱动力，滑移率近似为0，可以用前轮速折合为车速. 车速、车速加速度和加速度传感器测量值a，实现θ(k)中车辆质量m和道路坡度γ解耦.

3.1 控制器总体设计

基于驱动电机实现坡道静止保持的控制器原理如图4所示. 先判断档位，根据轮速判断是否要进行坡道静止. 因为车速低，假设车辆无滑移，则车速等于轮速，且有电机转速转换得出. 参数辨识中，利用电机q轴电流参数和转速参数，运用变遗忘因子最小二乘法估计，对车辆质量m和道路坡路γ进行辨识；在控制流程中，把整车作为控制对象，后移距离x为被控量输出，电机q轴电流iq为控制量，使用抗扰控制策略，把坡道变化、整车质量变动和电机参数变化，作为总扰动;使用ESO进行扰动观测，并使用PD控制率进行补偿控制，调整电机输出转矩Ts，满足坡道静止保持系统控制要求.

3.2 自抗扰控制器设计

文中分别采用一阶线性ADRC电流环[10]和二阶线性ADRC位置环，如图5所示. 电流控制量有两部分组成，一部分为参数辨识出的估算值，另一部分为期望电动车坡道静止保持期望值. 电流环的输入值为

(15)

设有二阶对象：

(16)

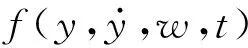
(17)

x3可通过三阶线性ESO进行观测，形式为

(18)

式中:

ωo为观测器带宽. 在适当设计扩张状态观测器后，控制器设计为

u=(-z3+u0)/b.

(19)

忽略误差z3，则控制器可设计为类似比例微分(PD)环，表示为

u0=kp(v-z1)-kdz2,

(20)

式中:kp=ωc2;kd=2ωc;ωc为控制器带宽;v*为参考值;p为被控对象和dis为扰动. 则二阶线性ADRC控制器结构如图6所示. ADRC 利用 ESO 估计受控对象状态变量和总扰动实时作用量，并给予补偿，从而设计出合理的控制器. 适当选取参数，能够提高系统控制准确度，使控制器具有较强的适应性和鲁棒性.

3.3 稳定性分析

从式(20)可知,z1,z2和z3可以表示为

(21)

(23)

则式 (21) 可转为

(24)

将z1,z2和z3代入式(24),可以得到传递函数

(25)

自抗扰算法的传递函数可表述成标准传递形式，如图7所示.

其中H(s)和Gc(s)分别为

(26)

(27)

从传递函数可知，开环传函Glp(s)和闭环传函Gcl(s)表达式可以方便得到

Glp(s)=Gc(s)Gp(s)=

(28)

(29)

式(25)～(29) 中的系数列于表1，令

a0=[19.288 938.56257.80777.006],

ωc=[1:1:100] rad/s，ωo=[1:1:1000]rad/s，

b0=[0.07770.07770.07770.0777].

闭环传函的Nyquist 分析如图8所示. 由图8可知，闭环系统没有包含(-1,0j)，所以系统稳定.

表1 系数列表

4 实验及数据分析

为验证所提出坡道驻车控制策略的有效性，在中国科学院电动汽车研发中心(天津)的实验平台进行了测试. 实验车辆为电动汽车，电池为72 V，100 A·h铅酸电池，具体参数见表2.

表2 系统参数

车辆在3个测试点分别有3个不同的车身角度，在C1点，前后轮都在坡道路面上；在C3点和C2点，后轮在平路面上，前轮在坡路面上. 测试点间距均为0.4 m，前轮轴线初始位置C1距离平整路面与坡道交界点1 m. 根据几何学原理，3个测试点的车辆倾角不一样. 实验中，乘客数量变化作为车辆总质量估算目标.

实验过程中，车速达到10 km/h，进入上坡工况，车辆依次经过点C3、C2和C1测试点，记录电机驱动电流，电机转速，质量估算值和角度估算值. 文中所提出的前段参数估计能有效估计出整车质量，并将误差控制在15%之内，实验中不同乘客数量的情况下，以及不同车辆倾角对质量估计的结果没有影响. 另外，对点C1、C2和C3的车辆倾角估计可以在坡度缓慢变化及快速变化时对当前坡度进行有效估计，估计误差基本满足了实车的实际需要. 当车辆无驱动电流时或断电时，上一时刻的估算值存入电机控制器的EEROM中，以作坡道驻车的转矩参考.

在经过车辆质量和路面坡度进行变遗忘因子最小二乘法估计基础上，进行坡道静止保持自抗扰控制. 实验中，为了便于测量车辆后移距离，车辆从测量点，松开刹车，档位为前进挡，无控制电流输入，然后，记录电机转速和车辆后移距离. 图9为3种ADRC试验方案和3种PI试验方案时电子驻车过程的车速数据；图10为ADRC与PI共6种试验方案时驻车过程的车辆后移距离；表3列出6种试验方案时驻车过程的负转速最大值和最大后移距离.

由图9可知，车辆加速度先负后正，且初始值较大. 较大加速度初始值会引起控制电流较大的峰值. 为了减少峰值电流对电机系统和车辆的冲击，需对电流值进行限制. 图6中位置环幅值饱和限制，一方面为控制车辆驻车响应速度，提升舒适性，另一方面，对电机控制器的功率器件进行保护.

由上述结果可见，车身倾角引起的外部扰动对车辆后移距离有影响，ADRC控制下负转速最大值和最大后移距离分别为PI控制下的 73.7%～87.1%及83.3%～84.2%. ADRC控制比PI控制，在响应速度和后移距离方面全面显著提升，驻车过程的抗扰性能优势显著.

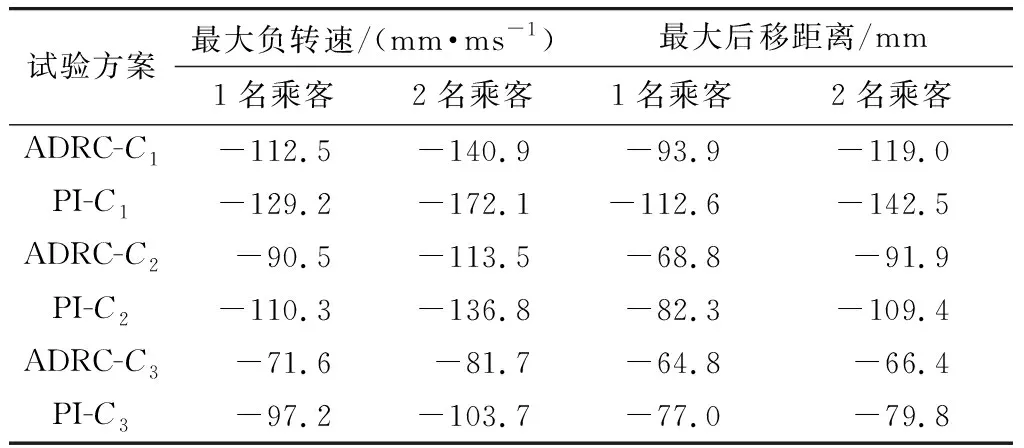
表3 静止保持控制实验结果

5 结 论

文中提出一种电动汽车的电机驱动静止保持系统，使车辆临时性静止于坡道，避免因后移造成安全隐患. 面对MSH系统的电机控制需求，文中使用变遗忘因子最小二乘法进行参数估计. 将估计出的车辆质量和路面坡度用于抗扰控制中，利用自抗扰控制器实时改变系统输出电磁转矩，进而提供匹配道阻力的驱动力，实现驻车目标. 实验结果表明，自抗扰控制器具有优异的扰动抑制能力和不依赖精确模型的特点，能够满足坡道静止保持控制要求. 将变遗忘因子最小二乘技术辨识和电机自抗扰控制器应用于电子驻车中，与PI控制器相比缩短了车辆后移距离，提高了系统响应速度，具备优良的控制性能.

相对于靠刹车系统实现坡道静止的自动保持系统，MSH系统利用原电机控制系统，不增加硬件成本，根据文中理论分析，可适用于所有电动汽车. 但是，MSH系统是耗能系统，电机运行在具有启动转矩且无转速的状态，若长时间坡道静止，对电机系统寿命不利. 因此，MSH系统可作为自动保持系统补充，提供一种新的坡道驻车方案.